Optimizadores de complementos de TensorFlow: ConditionalGradient, Optimizadores de complementos de TensorFlow: ConditionalGradient

Ver en TensorFlow.org Ejecutar en Google Colab Ver fuente en GitHub Descargar cuaderno

Visión general

Este cuaderno demostrará cómo utilizar Conditional Graident Optimizer del paquete de complementos.

ConditionalGradient

Se ha demostrado que restringir los parámetros de una red neuronal es beneficioso en el entrenamiento debido a los efectos de regularización subyacentes. A menudo, los parámetros están restringidos mediante una penalización suave (que nunca garantiza la satisfacción de la restricción) o mediante una operación de proyección (que es computacionalmente costosa). El optimizador de gradiente condicional (CG), por otro lado, aplica las restricciones estrictamente sin la necesidad de un paso de proyección costoso. Funciona minimizando una aproximación lineal del objetivo dentro del conjunto de restricciones. En este cuaderno, demuestra la aplicación de la restricción de la norma Frobenius a través del optimizador CG en el conjunto de datos MNIST. CG ahora está disponible como una API de tensorflow. Más detalles del optimizador están disponibles en https://arxiv.org/pdf/1803.06453.pdf

Configuración

pip install -q -U tensorflow-addons

import tensorflow as tf
import tensorflow_addons as tfa
from matplotlib import pyplot as plt

# Hyperparameters
batch_size=64
epochs=10

Construye el modelo

model_1 = tf.keras.Sequential([
    tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
    tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
    tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])

Prepara los datos

# Load MNIST dataset as NumPy arrays
dataset = {}
num_validation = 10000
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

# Preprocess the data
x_train = x_train.reshape(-1, 784).astype('float32') / 255
x_test = x_test.reshape(-1, 784).astype('float32') / 255

Definir una función de devolución de llamada personalizada

def frobenius_norm(m):
    """This function is to calculate the frobenius norm of the matrix of all
    layer's weight.

    Args:
        m: is a list of weights param for each layers.
    """
    total_reduce_sum = 0
    for i in range(len(m)):
        total_reduce_sum = total_reduce_sum + tf.math.reduce_sum(m[i]**2)
    norm = total_reduce_sum**0.5
    return norm

CG_frobenius_norm_of_weight = []
CG_get_weight_norm = tf.keras.callbacks.LambdaCallback(
    on_epoch_end=lambda batch, logs: CG_frobenius_norm_of_weight.append(
        frobenius_norm(model_1.trainable_weights).numpy()))

Entrenar y evaluar: uso de CG como optimizador

Simplemente reemplace los optimizadores de keras típicos con el nuevo optimizador de tfa

# Compile the model
model_1.compile(
    optimizer=tfa.optimizers.ConditionalGradient(
        learning_rate=0.99949, lambda_=203),  # Utilize TFA optimizer
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    metrics=['accuracy'])

history_cg = model_1.fit(
    x_train,
    y_train,
    batch_size=batch_size,
    validation_data=(x_test, y_test),
    epochs=epochs,
    callbacks=[CG_get_weight_norm])

Epoch 1/10
938/938 [==============================] - 4s 3ms/step - loss: 0.6034 - accuracy: 0.8162 - val_loss: 0.2282 - val_accuracy: 0.9313
Epoch 2/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1968 - accuracy: 0.9411 - val_loss: 0.1865 - val_accuracy: 0.9411
Epoch 3/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1502 - accuracy: 0.9552 - val_loss: 0.1356 - val_accuracy: 0.9590
Epoch 4/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1349 - accuracy: 0.9598 - val_loss: 0.1084 - val_accuracy: 0.9679
Epoch 5/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1261 - accuracy: 0.9609 - val_loss: 0.1162 - val_accuracy: 0.9648
Epoch 6/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1119 - accuracy: 0.9662 - val_loss: 0.1277 - val_accuracy: 0.9567
Epoch 7/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1096 - accuracy: 0.9671 - val_loss: 0.1009 - val_accuracy: 0.9685
Epoch 8/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1045 - accuracy: 0.9687 - val_loss: 0.1015 - val_accuracy: 0.9698
Epoch 9/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1011 - accuracy: 0.9688 - val_loss: 0.1180 - val_accuracy: 0.9627
Epoch 10/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1029 - accuracy: 0.9689 - val_loss: 0.1590 - val_accuracy: 0.9516

Capacitar y evaluar: uso de SGD como optimizador

model_2 = tf.keras.Sequential([
    tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
    tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
    tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])

SGD_frobenius_norm_of_weight = []
SGD_get_weight_norm = tf.keras.callbacks.LambdaCallback(
    on_epoch_end=lambda batch, logs: SGD_frobenius_norm_of_weight.append(
        frobenius_norm(model_2.trainable_weights).numpy()))

# Compile the model
model_2.compile(
    optimizer=tf.keras.optimizers.SGD(0.01),  # Utilize SGD optimizer
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    metrics=['accuracy'])

history_sgd = model_2.fit(
    x_train,
    y_train,
    batch_size=batch_size,
    validation_data=(x_test, y_test),
    epochs=epochs,
    callbacks=[SGD_get_weight_norm])

Epoch 1/10
938/938 [==============================] - 3s 3ms/step - loss: 1.4885 - accuracy: 0.5945 - val_loss: 0.4230 - val_accuracy: 0.8838
Epoch 2/10
938/938 [==============================] - 2s 2ms/step - loss: 0.4087 - accuracy: 0.8875 - val_loss: 0.3222 - val_accuracy: 0.9073
Epoch 3/10
938/938 [==============================] - 2s 2ms/step - loss: 0.3267 - accuracy: 0.9075 - val_loss: 0.2867 - val_accuracy: 0.9178
Epoch 4/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2903 - accuracy: 0.9186 - val_loss: 0.2605 - val_accuracy: 0.9259
Epoch 5/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2691 - accuracy: 0.9233 - val_loss: 0.2468 - val_accuracy: 0.9292
Epoch 6/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2466 - accuracy: 0.9291 - val_loss: 0.2265 - val_accuracy: 0.9352
Epoch 7/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2210 - accuracy: 0.9370 - val_loss: 0.2106 - val_accuracy: 0.9404
Epoch 8/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2137 - accuracy: 0.9387 - val_loss: 0.2029 - val_accuracy: 0.9424
Epoch 9/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1996 - accuracy: 0.9429 - val_loss: 0.1937 - val_accuracy: 0.9441
Epoch 10/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1925 - accuracy: 0.9450 - val_loss: 0.1831 - val_accuracy: 0.9469

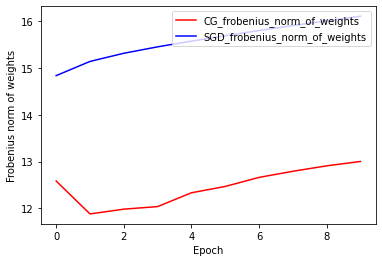
Norma de pesos de Frobenius: CG vs SGD

La implementación actual del optimizador CG se basa en Frobenius Norm, considerando Frobenius Norm como regularizador en la función de destino. Por lo tanto, compara el efecto regularizado de CG con el optimizador SGD, que no ha impuesto el regularizador Frobenius Norm.

plt.plot(
    CG_frobenius_norm_of_weight,
    color='r',
    label='CG_frobenius_norm_of_weights')
plt.plot(
    SGD_frobenius_norm_of_weight,
    color='b',
    label='SGD_frobenius_norm_of_weights')
plt.xlabel('Epoch')
plt.ylabel('Frobenius norm of weights')
plt.legend(loc=1)

<matplotlib.legend.Legend at 0x7fada7ab12e8>

png

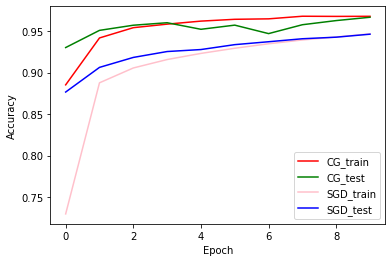
Precisión del tren y de la validación: CG vs SGD

plt.plot(history_cg.history['accuracy'], color='r', label='CG_train')
plt.plot(history_cg.history['val_accuracy'], color='g', label='CG_test')
plt.plot(history_sgd.history['accuracy'], color='pink', label='SGD_train')
plt.plot(history_sgd.history['val_accuracy'], color='b', label='SGD_test')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(loc=4)

<matplotlib.legend.Legend at 0x7fada7983e80>

png