 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
Este tutorial demostrará las mejores prácticas recomendadas para entrenar modelos con privacidad diferencial a nivel de usuario mediante Tensorflow Federated. Vamos a utilizar el algoritmo DP-SGD de Abadi et al., "Deep Learning en la vida privada diferencial" modificado para DP a nivel de usuario en un contexto federados en McMahan et al., "Modelos de aprendizaje diferencialmente privada recurrente de idioma" .
La privacidad diferencial (DP) es un método ampliamente utilizado para delimitar y cuantificar la fuga de privacidad de datos confidenciales al realizar tareas de aprendizaje. Entrenar un modelo con DP a nivel de usuario garantiza que es poco probable que el modelo aprenda algo significativo sobre los datos de cualquier individuo, pero aún puede (¡con suerte!) Aprender patrones que existen en los datos de muchos clientes.
Entrenaremos un modelo en el conjunto de datos EMNIST federado. Existe una compensación inherente entre la utilidad y la privacidad, y puede ser difícil entrenar un modelo con alta privacidad que funcione tan bien como un modelo no privado de última generación. Por conveniencia en este tutorial, entrenaremos por solo 100 rondas, sacrificando algo de calidad para demostrar cómo entrenar con alta privacidad. Si usáramos más rondas de entrenamiento, ciertamente podríamos tener un modelo privado de mayor precisión, pero no tan alto como un modelo entrenado sin DP.
Antes de que comencemos
Primero, asegurémonos de que el portátil esté conectado a un backend que tenga compilados los componentes relevantes.
!pip install --quiet --upgrade tensorflow_federated_nightly
!pip install --quiet --upgrade nest-asyncio
import nest_asyncio
nest_asyncio.apply()
Algunas importaciones que necesitaremos para el tutorial. Utilizaremos tensorflow_federated , el marco de código abierto para el aprendizaje de las máquinas y otros cálculos sobre los datos descentralizadas, así como tensorflow_privacy , la biblioteca de código abierto para la implementación y análisis de algoritmos diferencialmente privadas en tensorflow.
import collections
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_federated as tff
import tensorflow_privacy as tfp
Ejecute el siguiente ejemplo de "Hello World" para asegurarse de que el entorno TFF esté configurado correctamente. Si esto no funciona, por favor refiérase a la instalación de guía para obtener instrucciones.
@tff.federated_computation
def hello_world():
return 'Hello, World!'
hello_world()
b'Hello, World!'
Descargue y procese previamente el conjunto de datos EMNIST federado.
def get_emnist_dataset():
emnist_train, emnist_test = tff.simulation.datasets.emnist.load_data(
only_digits=True)
def element_fn(element):
return collections.OrderedDict(
x=tf.expand_dims(element['pixels'], -1), y=element['label'])
def preprocess_train_dataset(dataset):
# Use buffer_size same as the maximum client dataset size,
# 418 for Federated EMNIST
return (dataset.map(element_fn)
.shuffle(buffer_size=418)
.repeat(1)
.batch(32, drop_remainder=False))
def preprocess_test_dataset(dataset):
return dataset.map(element_fn).batch(128, drop_remainder=False)
emnist_train = emnist_train.preprocess(preprocess_train_dataset)
emnist_test = preprocess_test_dataset(
emnist_test.create_tf_dataset_from_all_clients())
return emnist_train, emnist_test
train_data, test_data = get_emnist_dataset()
Define nuestro modelo.
def my_model_fn():
model = tf.keras.models.Sequential([
tf.keras.layers.Reshape(input_shape=(28, 28, 1), target_shape=(28 * 28,)),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(10)])
return tff.learning.from_keras_model(
keras_model=model,
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
input_spec=test_data.element_spec,
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
Determine la sensibilidad al ruido del modelo.
Para obtener garantías de DP a nivel de usuario, debemos cambiar el algoritmo básico de promediado federado de dos maneras. Primero, las actualizaciones del modelo de los clientes deben recortarse antes de la transmisión al servidor, delimitando la influencia máxima de cualquier cliente. En segundo lugar, el servidor debe agregar suficiente ruido a la suma de las actualizaciones del usuario antes de promediar para ocultar la influencia del cliente en el peor de los casos.
Para el recorte, utilizamos el método de recorte de adaptación de Andrew et al. 2021, diferencialmente aprendizaje privado con Adaptive recorte , así que no hay norma recorte se debe establecer de forma explícita.
Agregar ruido degradará en general la utilidad del modelo, pero podemos controlar la cantidad de ruido en la actualización promedio en cada ronda con dos perillas: la desviación estándar del ruido gaussiano agregado a la suma y el número de clientes en el promedio. Nuestra estrategia será determinar primero cuánto ruido puede tolerar el modelo con un número relativamente pequeño de clientes por ronda con una pérdida aceptable de la utilidad del modelo. Luego, para entrenar el modelo final, podemos aumentar la cantidad de ruido en la suma, mientras aumentamos proporcionalmente el número de clientes por ronda (asumiendo que el conjunto de datos es lo suficientemente grande para admitir esa cantidad de clientes por ronda). Es poco probable que esto afecte significativamente la calidad del modelo, ya que el único efecto es disminuir la varianza debido al muestreo del cliente (de hecho, verificaremos que no es así en nuestro caso).
Con ese fin, primero entrenamos una serie de modelos con 50 clientes por ronda, con cantidades crecientes de ruido. Específicamente, aumentamos el "ruido_multiplicador", que es la relación entre la desviación estándar de ruido y la norma de recorte. Dado que estamos usando el recorte adaptativo, esto significa que la magnitud real del ruido cambia de redondo a redondo.
# Run five clients per thread. Increase this if your runtime is running out of
# memory. Decrease it if you have the resources and want to speed up execution.
tff.backends.native.set_local_python_execution_context(clients_per_thread=5)
total_clients = len(train_data.client_ids)
def train(rounds, noise_multiplier, clients_per_round, data_frame):
# Using the `dp_aggregator` here turns on differential privacy with adaptive
# clipping.
aggregation_factory = tff.learning.model_update_aggregator.dp_aggregator(
noise_multiplier, clients_per_round)
# We use Poisson subsampling which gives slightly tighter privacy guarantees
# compared to having a fixed number of clients per round. The actual number of
# clients per round is stochastic with mean clients_per_round.
sampling_prob = clients_per_round / total_clients
# Build a federated averaging process.
# Typically a non-adaptive server optimizer is used because the noise in the
# updates can cause the second moment accumulators to become very large
# prematurely.
learning_process = tff.learning.build_federated_averaging_process(
my_model_fn,
client_optimizer_fn=lambda: tf.keras.optimizers.SGD(0.01),
server_optimizer_fn=lambda: tf.keras.optimizers.SGD(1.0, momentum=0.9),
model_update_aggregation_factory=aggregation_factory)
eval_process = tff.learning.build_federated_evaluation(my_model_fn)
# Training loop.
state = learning_process.initialize()
for round in range(rounds):
if round % 5 == 0:
metrics = eval_process(state.model, [test_data])['eval']
if round < 25 or round % 25 == 0:
print(f'Round {round:3d}: {metrics}')
data_frame = data_frame.append({'Round': round,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
# Sample clients for a round. Note that if your dataset is large and
# sampling_prob is small, it would be faster to use gap sampling.
x = np.random.uniform(size=total_clients)
sampled_clients = [
train_data.client_ids[i] for i in range(total_clients)
if x[i] < sampling_prob]
sampled_train_data = [
train_data.create_tf_dataset_for_client(client)
for client in sampled_clients]
# Use selected clients for update.
state, metrics = learning_process.next(state, sampled_train_data)
metrics = eval_process(state.model, [test_data])['eval']
print(f'Round {rounds:3d}: {metrics}')
data_frame = data_frame.append({'Round': rounds,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
return data_frame
data_frame = pd.DataFrame()
rounds = 100
clients_per_round = 50
for noise_multiplier in [0.0, 0.5, 0.75, 1.0]:
print(f'Starting training with noise multiplier: {noise_multiplier}')
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
print()
Starting training with noise multiplier: 0.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.112289384), ('loss', 2.5190482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.19075724), ('loss', 2.2449977)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.18115693), ('loss', 2.163907)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49970612), ('loss', 2.01017)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5333317), ('loss', 1.8350543)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.5828517), ('loss', 1.6551636)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7352077), ('loss', 0.8700141)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7769152), ('loss', 0.6992781)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.8049814), ('loss', 0.62453026)])
Starting training with noise multiplier: 0.5
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.09526841), ('loss', 2.4332638)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.20128821), ('loss', 2.2664592)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.35472178), ('loss', 2.130336)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.5480995), ('loss', 1.9713942)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.42246276), ('loss', 1.8045483)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.624902), ('loss', 1.4785467)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7265625), ('loss', 0.85801566)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.77720904), ('loss', 0.70615387)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7702537), ('loss', 0.72331005)])
Starting training with noise multiplier: 0.75
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.098672606), ('loss', 2.422002)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.11794671), ('loss', 2.2227976)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.3208513), ('loss', 2.083766)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49752644), ('loss', 1.8728142)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5816761), ('loss', 1.6084186)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.62896746), ('loss', 1.378527)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.73153406), ('loss', 0.8705139)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7789724), ('loss', 0.7113147)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.70944357), ('loss', 0.89495045)])
Starting training with noise multiplier: 1.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.12002841), ('loss', 2.60482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.104574844), ('loss', 2.3388205)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.29966694), ('loss', 2.089262)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.4067398), ('loss', 1.9109797)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5123677), ('loss', 1.6472703)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.56416535), ('loss', 1.4362282)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.62323666), ('loss', 1.1682972)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.55968356), ('loss', 1.4779186)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.382837), ('loss', 1.9680436)])
Ahora podemos visualizar la precisión del conjunto de evaluación y la pérdida de esas ejecuciones.
import matplotlib.pyplot as plt
import seaborn as sns
def make_plot(data_frame):
plt.figure(figsize=(15, 5))
dff = data_frame.rename(
columns={'sparse_categorical_accuracy': 'Accuracy', 'loss': 'Loss'})
plt.subplot(121)
sns.lineplot(data=dff, x='Round', y='Accuracy', hue='NoiseMultiplier', palette='dark')
plt.subplot(122)
sns.lineplot(data=dff, x='Round', y='Loss', hue='NoiseMultiplier', palette='dark')
make_plot(data_frame)
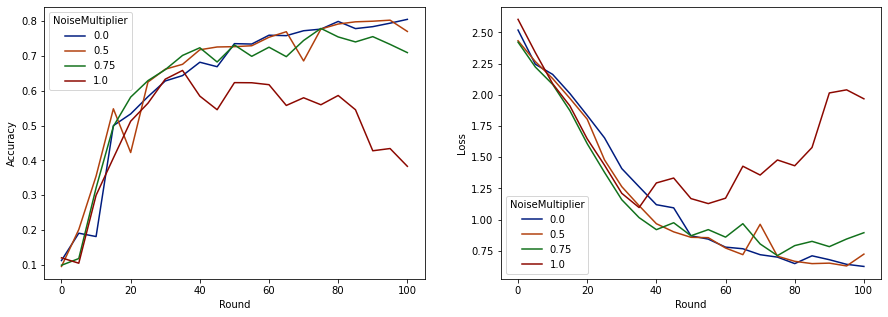
Parece que con 50 clientes esperados por ronda, este modelo puede tolerar un multiplicador de ruido de hasta 0,5 sin degradar la calidad del modelo. Un multiplicador de ruido de 0,75 parece causar un poco de degradación del modelo y 1,0 hace que el modelo diverja.
Por lo general, existe una compensación entre la calidad del modelo y la privacidad. Cuanto mayor sea el ruido que usemos, más privacidad podremos obtener para la misma cantidad de tiempo de capacitación y número de clientes. Por el contrario, con menos ruido, es posible que tengamos un modelo más preciso, pero tendremos que entrenar con más clientes por ronda para alcanzar nuestro nivel de privacidad objetivo.
Con el experimento anterior, podríamos decidir que la pequeña cantidad de deterioro del modelo en 0,75 es aceptable para entrenar el modelo final más rápido, pero supongamos que queremos igualar el rendimiento del modelo de multiplicador de ruido de 0,5.
Ahora podemos usar las funciones de tensorflow_privacy para determinar cuántos clientes esperados por ronda necesitaríamos para obtener una privacidad aceptable. La práctica estándar es elegir un delta algo menor que uno sobre el número de registros en el conjunto de datos. Este conjunto de datos tiene 3383 usuarios de entrenamiento en total, así que apuntemos a (2, 1e-5) -DP.
Usamos una búsqueda binaria simple sobre el número de clientes por ronda. La función tensorflow_privacy que utilizamos para estimar épsilon se basa en Wang et al. (2018) y Mironov et al. (2019) .
rdp_orders = ([1.25, 1.5, 1.75, 2., 2.25, 2.5, 3., 3.5, 4., 4.5] +
list(range(5, 64)) + [128, 256, 512])
total_clients = 3383
base_noise_multiplier = 0.5
base_clients_per_round = 50
target_delta = 1e-5
target_eps = 2
def get_epsilon(clients_per_round):
# If we use this number of clients per round and proportionally
# scale up the noise multiplier, what epsilon do we achieve?
q = clients_per_round / total_clients
noise_multiplier = base_noise_multiplier
noise_multiplier *= clients_per_round / base_clients_per_round
rdp = tfp.compute_rdp(
q, noise_multiplier=noise_multiplier, steps=rounds, orders=rdp_orders)
eps, _, _ = tfp.get_privacy_spent(rdp_orders, rdp, target_delta=target_delta)
return clients_per_round, eps, noise_multiplier
def find_needed_clients_per_round():
hi = get_epsilon(base_clients_per_round)
if hi[1] < target_eps:
return hi
# Grow interval exponentially until target_eps is exceeded.
while True:
lo = hi
hi = get_epsilon(2 * lo[0])
if hi[1] < target_eps:
break
# Binary search.
while hi[0] - lo[0] > 1:
mid = get_epsilon((lo[0] + hi[0]) // 2)
if mid[1] > target_eps:
lo = mid
else:
hi = mid
return hi
clients_per_round, _, noise_multiplier = find_needed_clients_per_round()
print(f'To get ({target_eps}, {target_delta})-DP, use {clients_per_round} '
f'clients with noise multiplier {noise_multiplier}.')
To get (2, 1e-05)-DP, use 120 clients with noise multiplier 1.2.
Ahora podemos entrenar nuestro modelo privado final para su lanzamiento.
rounds = 100
noise_multiplier = 1.2
clients_per_round = 120
data_frame = pd.DataFrame()
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
make_plot(data_frame)
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.08260678), ('loss', 2.6334999)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.1492212), ('loss', 2.259542)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.28847474), ('loss', 2.155699)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.3989518), ('loss', 2.0156953)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5086697), ('loss', 1.8261365)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.6204692), ('loss', 1.5602393)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.70008814), ('loss', 0.91155165)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.78421336), ('loss', 0.6820159)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7955525), ('loss', 0.6585961)])
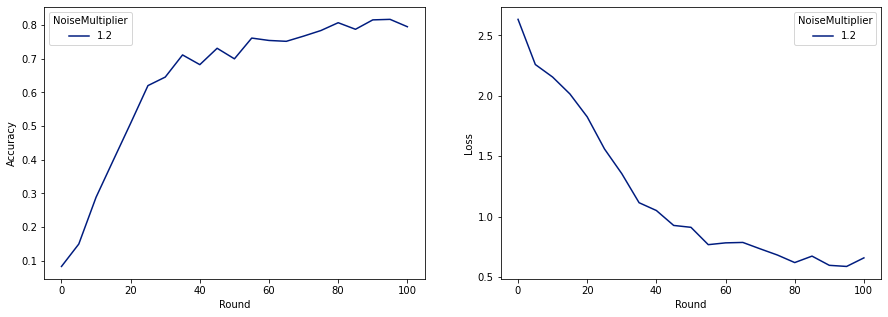
Como podemos ver, el modelo final tiene una pérdida y precisión similar al modelo entrenado sin ruido, pero este satisface (2, 1e-5) -DP.

