View on TensorFlow.org View on TensorFlow.org
|
 Run in Google Colab Run in Google Colab
|
 View source on GitHub View source on GitHub
|
 Download notebook Download notebook
|
Overview
GPUs and TPUs can radically reduce the time required to execute a single training step.
Achieving peak performance requires an efficient input pipeline that delivers data for the next step before the current step has finished.
The tf.data API helps to build flexible and efficient input pipelines.
This document demonstrates how to use the tf.data API to build highly performant TensorFlow input pipelines.
Before you continue, check the Build TensorFlow input pipelines guide to learn how to use the tf.data API.
Resources
- Build TensorFlow input pipelines
tf.data.DatasetAPI- Analyze
tf.dataperformance with the TF Profiler
Setup
import tensorflow as tf
import time
2023-09-28 01:23:33.839755: E tensorflow/compiler/xla/stream_executor/cuda/cuda_dnn.cc:9342] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered 2023-09-28 01:23:33.839805: E tensorflow/compiler/xla/stream_executor/cuda/cuda_fft.cc:609] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered 2023-09-28 01:23:33.839842: E tensorflow/compiler/xla/stream_executor/cuda/cuda_blas.cc:1518] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered
Throughout this guide, you will iterate across a dataset and measure the performance. Making reproducible performance benchmarks can be difficult. Different factors affecting reproducibility include:
- The current CPU load
- The network traffic
- Complex mechanisms, such as cache
To get a reproducible benchmark, you will build an artificial example.
The dataset
Start with defining a class inheriting from tf.data.Dataset called ArtificialDataset.
This dataset:
- Generates
num_samplessamples (default is 3) - Sleeps for some time before the first item to simulate opening a file
- Sleeps for some time before producing each item to simulate reading data from a file
class ArtificialDataset(tf.data.Dataset):
def _generator(num_samples):
# Opening the file
time.sleep(0.03)
for sample_idx in range(num_samples):
# Reading data (line, record) from the file
time.sleep(0.015)
yield (sample_idx,)
def __new__(cls, num_samples=3):
return tf.data.Dataset.from_generator(
cls._generator,
output_signature = tf.TensorSpec(shape = (1,), dtype = tf.int64),
args=(num_samples,)
)
This dataset is similar to the tf.data.Dataset.range one, adding a fixed delay at the beginning of and in-between each sample.
The training loop
Next, write a dummy training loop that measures how long it takes to iterate over a dataset. Training time is simulated.
def benchmark(dataset, num_epochs=2):
start_time = time.perf_counter()
for epoch_num in range(num_epochs):
for sample in dataset:
# Performing a training step
time.sleep(0.01)
print("Execution time:", time.perf_counter() - start_time)
Optimize performance
To exhibit how performance can be optimized, you will improve the performance of the ArtificialDataset.
The naive approach
Start with a naive pipeline using no tricks, iterating over the dataset as-is.
benchmark(ArtificialDataset())
2023-09-28 01:23:36.616209: W tensorflow/core/common_runtime/gpu/gpu_device.cc:2211] Cannot dlopen some GPU libraries. Please make sure the missing libraries mentioned above are installed properly if you would like to use GPU. Follow the guide at https://www.tensorflow.org/install/gpu for how to download and setup the required libraries for your platform. Skipping registering GPU devices... Execution time: 0.22170253400008733
Under the hood, this is how your execution time was spent:
The plot shows that performing a training step involves:
- Opening a file if it hasn't been opened yet
- Fetching a data entry from the file
- Using the data for training
However, in a naive synchronous implementation like here, while your pipeline is fetching the data, your model is sitting idle. Conversely, while your model is training, the input pipeline is sitting idle. The training step time is thus the sum of opening, reading and training times.
The next sections build on this input pipeline, illustrating best practices for designing performant TensorFlow input pipelines.
Prefetching
Prefetching overlaps the preprocessing and model execution of a training step.
While the model is executing training step s, the input pipeline is reading the data for step s+1.
Doing so reduces the step time to the maximum (as opposed to the sum) of the training and the time it takes to extract the data.
The tf.data API provides the tf.data.Dataset.prefetch transformation.
It can be used to decouple the time when data is produced from the time when data is consumed.
In particular, the transformation uses a background thread and an internal buffer to prefetch elements from the input dataset ahead of the time they are requested.
The number of elements to prefetch should be equal to (or possibly greater than) the number of batches consumed by a single training step.
You could either manually tune this value, or set it to tf.data.AUTOTUNE, which will prompt the
tf.data runtime to tune the value dynamically at runtime.
Note that the prefetch transformation provides benefits any time there is an opportunity to overlap the work of a "producer" with the work of a "consumer."
benchmark(
ArtificialDataset()
.prefetch(tf.data.AUTOTUNE)
)
Execution time: 0.21934373199997026
Now, as the data execution time plot shows, while the training step is running for sample 0, the input pipeline is reading the data for the sample 1, and so on.
Parallelizing data extraction
In a real-world setting, the input data may be stored remotely (for example, on Google Cloud Storage or HDFS). A dataset pipeline that works well when reading data locally might become bottlenecked on I/O when reading data remotely because of the following differences between local and remote storage:
- Time-to-first-byte: Reading the first byte of a file from remote storage can take orders of magnitude longer than from local storage.
- Read throughput: While remote storage typically offers large aggregate bandwidth, reading a single file might only be able to utilize a small fraction of this bandwidth.
In addition, once the raw bytes are loaded into memory, it may also be necessary to deserialize and/or decrypt the data (e.g. protobuf), which requires additional computation. This overhead is present irrespective of whether the data is stored locally or remotely, but can be worse in the remote case if data is not prefetched effectively.
To mitigate the impact of the various data extraction overheads, the tf.data.Dataset.interleave transformation can be used to parallelize the data loading step, interleaving the contents of other datasets (such as data file
readers).
The number of datasets to overlap can be specified by the cycle_length argument, while the level of parallelism can be specified by the num_parallel_calls argument. Similar to the prefetch transformation, the interleave transformation supports tf.data.AUTOTUNE, which will delegate the decision about what level of parallelism to use to the tf.data runtime.
Sequential interleave
The default arguments of the tf.data.Dataset.interleave transformation make it interleave single samples from two datasets sequentially.
benchmark(
tf.data.Dataset.range(2)
.interleave(lambda _: ArtificialDataset())
)
Execution time: 0.3967778650001037
This data execution time plot allows to exhibit the behavior of the interleave transformation, fetching samples alternatively from the two datasets available.
However, no performance improvement is involved here.
Parallel interleave
Now, use the num_parallel_calls argument of the interleave transformation.
This loads multiple datasets in parallel, reducing the time waiting for the files to be opened.
benchmark(
tf.data.Dataset.range(2)
.interleave(
lambda _: ArtificialDataset(),
num_parallel_calls=tf.data.AUTOTUNE
)
)
Execution time: 0.29122259999985545
This time, as the data execution time plot shows, the reading of the two datasets is parallelized, reducing the global data processing time.
Parallelizing data transformation
When preparing data, input elements may need to be pre-processed.
To this end, the tf.data API offers the tf.data.Dataset.map transformation, which applies a user-defined function to each element of the input dataset.
Because input elements are independent of one another, the pre-processing can be parallelized across multiple CPU cores.
To make this possible, similarly to the prefetch and interleave transformations, the map transformation provides the num_parallel_calls argument to specify the level of parallelism.
Choosing the best value for the num_parallel_calls argument depends on your hardware, characteristics of your training data (such as its size and shape), the cost of your map function, and what other processing is happening on the CPU at the same time.
A simple heuristic is to use the number of available CPU cores.
However, as for the prefetch and interleave transformation, the map transformation supports tf.data.AUTOTUNE which will delegate the decision about what level of parallelism to use to the tf.data runtime.
def mapped_function(s):
# Do some hard pre-processing
tf.py_function(lambda: time.sleep(0.03), [], ())
return s
Sequential mapping
Start by using the map transformation without parallelism as a baseline example.
benchmark(
ArtificialDataset()
.map(mapped_function)
)
Execution time: 0.40914792600005967
As for the naive approach, here, as the plot shows, the times spent for opening, reading, pre-processing (mapping) and training steps sum together for a single iteration.
Parallel mapping
Now, use the same pre-processing function but apply it in parallel on multiple samples.
benchmark(
ArtificialDataset()
.map(
mapped_function,
num_parallel_calls=tf.data.AUTOTUNE
)
)
Execution time: 0.2876913739999054
As the data plot demonstrates, the pre-processing steps overlap, reducing the overall time for a single iteration.
Caching
The tf.data.Dataset.cache transformation can cache a dataset, either in memory or on local storage.
This will save some operations (like file opening and data reading) from being executed during each epoch.
benchmark(
ArtificialDataset()
.map( # Apply time consuming operations before cache
mapped_function
).cache(
),
5
)
Execution time: 0.3480471000000307
Here, the data execution time plot shows that when you cache a dataset, the transformations before the cache one (like the file opening and data reading) are executed only during the first epoch.
The next epochs will reuse the data cached by thecache transformation.
If the user-defined function passed into the map transformation is expensive, apply the cache transformation after the map transformation as long as the resulting dataset can still fit into memory or local storage.
If the user-defined function increases the space required to store the dataset beyond the cache capacity, either apply it after the cache transformation or consider pre-processing your data before your training job to reduce resource usage.
Vectorizing mapping
Invoking a user-defined function passed into the map transformation has overhead related to scheduling and executing the user-defined function.
Vectorize the user-defined function (that is, have it operate over a batch of inputs at once) and apply the batch transformation before the map transformation.
To illustrate this good practice, your artificial dataset is not suitable.
The scheduling delay is around 10 microseconds (10e-6 seconds), far less than the tens of milliseconds used in the ArtificialDataset, and thus its impact is hard to see.
For this example, use the base tf.data.Dataset.range function and simplify the training loop to its simplest form.
fast_dataset = tf.data.Dataset.range(10000)
def fast_benchmark(dataset, num_epochs=2):
start_time = time.perf_counter()
for _ in tf.data.Dataset.range(num_epochs):
for _ in dataset:
pass
tf.print("Execution time:", time.perf_counter() - start_time)
def increment(x):
return x+1
Scalar mapping
fast_benchmark(
fast_dataset
# Apply function one item at a time
.map(increment)
# Batch
.batch(256)
)
Execution time: 0.2002891649999583
The plot above illustrates what is going on (with less samples) using the scalar mapping method. It shows that the mapped function is applied for each sample. While this function is very fast, it has some overhead that impact the time performance.
Vectorized mapping
fast_benchmark(
fast_dataset
.batch(256)
# Apply function on a batch of items
# The tf.Tensor.__add__ method already handle batches
.map(increment)
)
Execution time: 0.03308858700006567
This time, the mapped function is called once and applies to a batch of sample. As the data execution time plot shows, while the function could takes more time to execute, the overhead appear only once, improving the overall time performance.
Reducing memory footprint
A number of transformations, including interleave, prefetch, and shuffle, maintain an internal buffer of elements. If the user-defined function passed into the map transformation changes the size of the elements, then the ordering of the map transformation and the transformations that buffer elements affects the memory usage. In general, choose the order that results in lower memory footprint, unless different ordering is desirable for performance.
Caching partial computations
It is recommended to cache the dataset after the map transformation except if this transformation makes the data too big to fit in memory.
A trade-off can be achieved if your mapped function can be split in two parts: a time consuming one and a memory consuming part.
In this case, you can chain your transformations like below:
dataset.map(time_consuming_mapping).cache().map(memory_consuming_mapping)
This way, the time consuming part is only executed during the first epoch, and you avoid using too much cache space.
Best practice summary
Here is a summary of the best practices for designing performant TensorFlow input pipelines:
- Use the
prefetchtransformation to overlap the work of a producer and consumer - Parallelize the data reading transformation using the
interleavetransformation - Parallelize the
maptransformation by setting thenum_parallel_callsargument - Use the
cachetransformation to cache data in memory during the first epoch - Vectorize user-defined functions passed in to the
maptransformation - Reduce memory usage when applying the
interleave,prefetch, andshuffletransformations
Reproducing the figures
To go deeper in the tf.data.Dataset API understanding, you can play with your own pipelines.
Below is the code used to plot the images from this guide.
It can be a good starting point, showing some workarounds for common difficulties such as:
- Execution time reproducibility
- Mapped functions eager execution
interleavetransformation callable
import itertools
from collections import defaultdict
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
The dataset
Similar to the ArtificialDataset you can build a dataset returning the time spent in each step.
class TimeMeasuredDataset(tf.data.Dataset):
# OUTPUT: (steps, timings, counters)
OUTPUT_TYPES = (tf.dtypes.string, tf.dtypes.float32, tf.dtypes.int32)
OUTPUT_SHAPES = ((2, 1), (2, 2), (2, 3))
_INSTANCES_COUNTER = itertools.count() # Number of datasets generated
_EPOCHS_COUNTER = defaultdict(itertools.count) # Number of epochs done for each dataset
def _generator(instance_idx, num_samples):
epoch_idx = next(TimeMeasuredDataset._EPOCHS_COUNTER[instance_idx])
# Opening the file
open_enter = time.perf_counter()
time.sleep(0.03)
open_elapsed = time.perf_counter() - open_enter
for sample_idx in range(num_samples):
# Reading data (line, record) from the file
read_enter = time.perf_counter()
time.sleep(0.015)
read_elapsed = time.perf_counter() - read_enter
yield (
[("Open",), ("Read",)],
[(open_enter, open_elapsed), (read_enter, read_elapsed)],
[(instance_idx, epoch_idx, -1), (instance_idx, epoch_idx, sample_idx)]
)
open_enter, open_elapsed = -1., -1. # Negative values will be filtered
def __new__(cls, num_samples=3):
return tf.data.Dataset.from_generator(
cls._generator,
output_types=cls.OUTPUT_TYPES,
output_shapes=cls.OUTPUT_SHAPES,
args=(next(cls._INSTANCES_COUNTER), num_samples)
)
This dataset provides samples of shape [[2, 1], [2, 2], [2, 3]] and of type [tf.dtypes.string, tf.dtypes.float32, tf.dtypes.int32].
Each sample is:
(
[("Open"), ("Read")],
[(t0, d), (t0, d)],
[(i, e, -1), (i, e, s)]
)
Where:
OpenandReadare steps identifierst0is the timestamp when the corresponding step starteddis the time spent in the corresponding stepiis the instance indexeis the epoch index (number of times the dataset has been iterated)sis the sample index
The iteration loop
Make the iteration loop a little bit more complicated to aggregate all timings. This will only work with datasets generating samples as detailed above.
def timelined_benchmark(dataset, num_epochs=2):
# Initialize accumulators
steps_acc = tf.zeros([0, 1], dtype=tf.dtypes.string)
times_acc = tf.zeros([0, 2], dtype=tf.dtypes.float32)
values_acc = tf.zeros([0, 3], dtype=tf.dtypes.int32)
start_time = time.perf_counter()
for epoch_num in range(num_epochs):
epoch_enter = time.perf_counter()
for (steps, times, values) in dataset:
# Record dataset preparation informations
steps_acc = tf.concat((steps_acc, steps), axis=0)
times_acc = tf.concat((times_acc, times), axis=0)
values_acc = tf.concat((values_acc, values), axis=0)
# Simulate training time
train_enter = time.perf_counter()
time.sleep(0.01)
train_elapsed = time.perf_counter() - train_enter
# Record training informations
steps_acc = tf.concat((steps_acc, [["Train"]]), axis=0)
times_acc = tf.concat((times_acc, [(train_enter, train_elapsed)]), axis=0)
values_acc = tf.concat((values_acc, [values[-1]]), axis=0)
epoch_elapsed = time.perf_counter() - epoch_enter
# Record epoch informations
steps_acc = tf.concat((steps_acc, [["Epoch"]]), axis=0)
times_acc = tf.concat((times_acc, [(epoch_enter, epoch_elapsed)]), axis=0)
values_acc = tf.concat((values_acc, [[-1, epoch_num, -1]]), axis=0)
time.sleep(0.001)
tf.print("Execution time:", time.perf_counter() - start_time)
return {"steps": steps_acc, "times": times_acc, "values": values_acc}
The plotting method
Finally, define a function able to plot a timeline given the values returned by the timelined_benchmark function.
def draw_timeline(timeline, title, width=0.5, annotate=False, save=False):
# Remove invalid entries (negative times, or empty steps) from the timelines
invalid_mask = np.logical_and(timeline['times'] > 0, timeline['steps'] != b'')[:,0]
steps = timeline['steps'][invalid_mask].numpy()
times = timeline['times'][invalid_mask].numpy()
values = timeline['values'][invalid_mask].numpy()
# Get a set of different steps, ordered by the first time they are encountered
step_ids, indices = np.stack(np.unique(steps, return_index=True))
step_ids = step_ids[np.argsort(indices)]
# Shift the starting time to 0 and compute the maximal time value
min_time = times[:,0].min()
times[:,0] = (times[:,0] - min_time)
end = max(width, (times[:,0]+times[:,1]).max() + 0.01)
cmap = mpl.cm.get_cmap("plasma")
plt.close()
fig, axs = plt.subplots(len(step_ids), sharex=True, gridspec_kw={'hspace': 0})
fig.suptitle(title)
fig.set_size_inches(17.0, len(step_ids))
plt.xlim(-0.01, end)
for i, step in enumerate(step_ids):
step_name = step.decode()
ax = axs[i]
ax.set_ylabel(step_name)
ax.set_ylim(0, 1)
ax.set_yticks([])
ax.set_xlabel("time (s)")
ax.set_xticklabels([])
ax.grid(which="both", axis="x", color="k", linestyle=":")
# Get timings and annotation for the given step
entries_mask = np.squeeze(steps==step)
serie = np.unique(times[entries_mask], axis=0)
annotations = values[entries_mask]
ax.broken_barh(serie, (0, 1), color=cmap(i / len(step_ids)), linewidth=1, alpha=0.66)
if annotate:
for j, (start, width) in enumerate(serie):
annotation = "\n".join([f"{l}: {v}" for l,v in zip(("i", "e", "s"), annotations[j])])
ax.text(start + 0.001 + (0.001 * (j % 2)), 0.55 - (0.1 * (j % 2)), annotation,
horizontalalignment='left', verticalalignment='center')
if save:
plt.savefig(title.lower().translate(str.maketrans(" ", "_")) + ".svg")
Use wrappers for mapped function
To run mapped function in an eager context, you have to wrap them inside a tf.py_function call.
def map_decorator(func):
def wrapper(steps, times, values):
# Use a tf.py_function to prevent auto-graph from compiling the method
return tf.py_function(
func,
inp=(steps, times, values),
Tout=(steps.dtype, times.dtype, values.dtype)
)
return wrapper
Pipelines comparison
_batch_map_num_items = 50
def dataset_generator_fun(*args):
return TimeMeasuredDataset(num_samples=_batch_map_num_items)
Naive
@map_decorator
def naive_map(steps, times, values):
map_enter = time.perf_counter()
time.sleep(0.001) # Time consuming step
time.sleep(0.0001) # Memory consuming step
map_elapsed = time.perf_counter() - map_enter
return (
tf.concat((steps, [["Map"]]), axis=0),
tf.concat((times, [[map_enter, map_elapsed]]), axis=0),
tf.concat((values, [values[-1]]), axis=0)
)
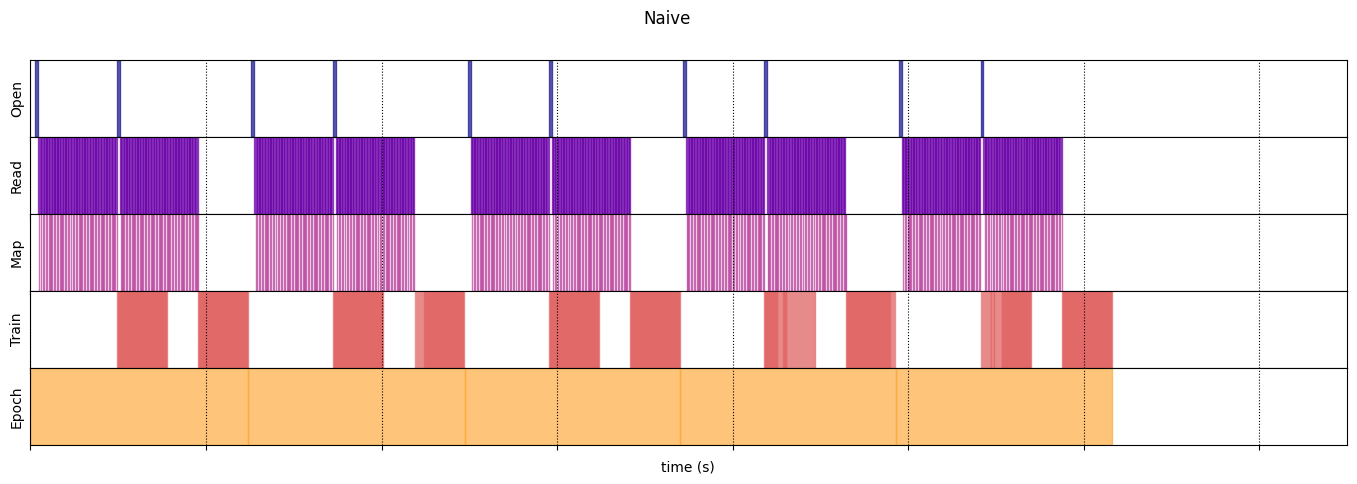
naive_timeline = timelined_benchmark(
tf.data.Dataset.range(2)
.flat_map(dataset_generator_fun)
.map(naive_map)
.batch(_batch_map_num_items, drop_remainder=True)
.unbatch(),
5
)
WARNING:tensorflow:From /tmpfs/tmp/ipykernel_13942/64197174.py:32: calling DatasetV2.from_generator (from tensorflow.python.data.ops.dataset_ops) with output_types is deprecated and will be removed in a future version. Instructions for updating: Use output_signature instead WARNING:tensorflow:From /tmpfs/tmp/ipykernel_13942/64197174.py:32: calling DatasetV2.from_generator (from tensorflow.python.data.ops.dataset_ops) with output_shapes is deprecated and will be removed in a future version. Instructions for updating: Use output_signature instead Execution time: 12.326121639000121
Optimized
@map_decorator
def time_consuming_map(steps, times, values):
map_enter = time.perf_counter()
time.sleep(0.001 * values.shape[0]) # Time consuming step
map_elapsed = time.perf_counter() - map_enter
return (
tf.concat((steps, tf.tile([[["1st map"]]], [steps.shape[0], 1, 1])), axis=1),
tf.concat((times, tf.tile([[[map_enter, map_elapsed]]], [times.shape[0], 1, 1])), axis=1),
tf.concat((values, tf.tile([[values[:][-1][0]]], [values.shape[0], 1, 1])), axis=1)
)
@map_decorator
def memory_consuming_map(steps, times, values):
map_enter = time.perf_counter()
time.sleep(0.0001 * values.shape[0]) # Memory consuming step
map_elapsed = time.perf_counter() - map_enter
# Use tf.tile to handle batch dimension
return (
tf.concat((steps, tf.tile([[["2nd map"]]], [steps.shape[0], 1, 1])), axis=1),
tf.concat((times, tf.tile([[[map_enter, map_elapsed]]], [times.shape[0], 1, 1])), axis=1),
tf.concat((values, tf.tile([[values[:][-1][0]]], [values.shape[0], 1, 1])), axis=1)
)
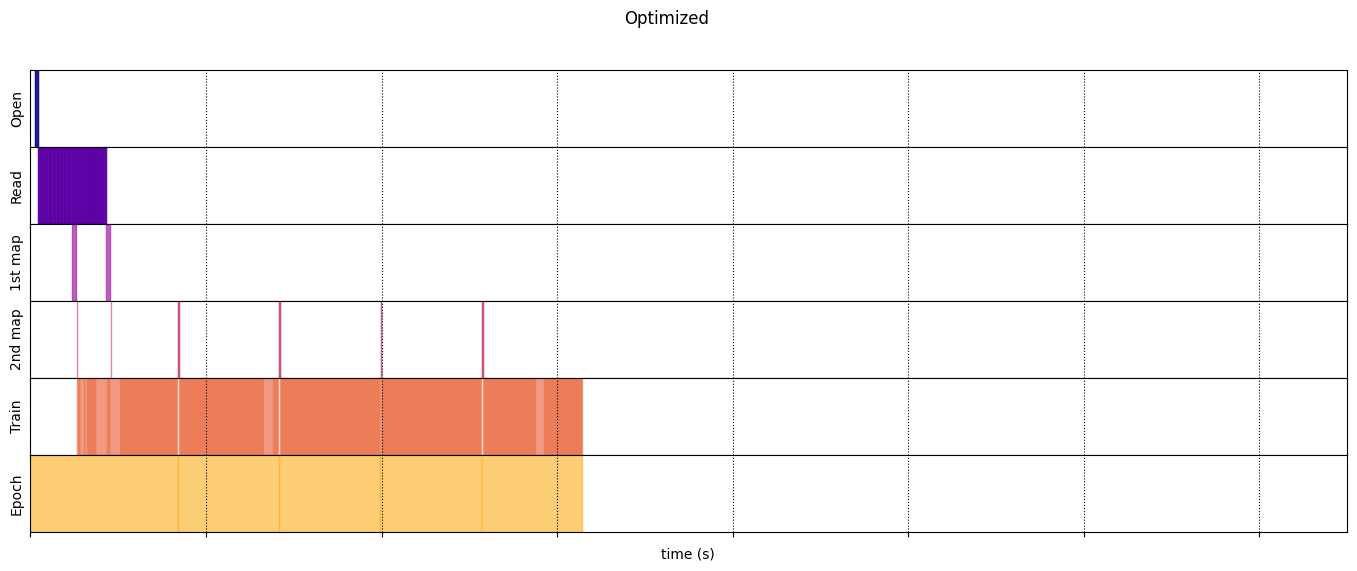
optimized_timeline = timelined_benchmark(
tf.data.Dataset.range(2)
.interleave( # Parallelize data reading
dataset_generator_fun,
num_parallel_calls=tf.data.AUTOTUNE
)
.batch( # Vectorize your mapped function
_batch_map_num_items,
drop_remainder=True)
.map( # Parallelize map transformation
time_consuming_map,
num_parallel_calls=tf.data.AUTOTUNE
)
.cache() # Cache data
.map( # Reduce memory usage
memory_consuming_map,
num_parallel_calls=tf.data.AUTOTUNE
)
.prefetch( # Overlap producer and consumer works
tf.data.AUTOTUNE
)
.unbatch(),
5
)
Execution time: 6.28881555199996
draw_timeline(naive_timeline, "Naive", 15)
/tmpfs/tmp/ipykernel_13942/2966908191.py:17: MatplotlibDeprecationWarning: The get_cmap function was deprecated in Matplotlib 3.7 and will be removed two minor releases later. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap(obj)`` instead.
cmap = mpl.cm.get_cmap("plasma")
draw_timeline(optimized_timeline, "Optimized", 15)
/tmpfs/tmp/ipykernel_13942/2966908191.py:17: MatplotlibDeprecationWarning: The get_cmap function was deprecated in Matplotlib 3.7 and will be removed two minor releases later. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap(obj)`` instead.
cmap = mpl.cm.get_cmap("plasma")