Google I/O — это обертка! Наверстать упущенное в сеансах TensorFlow Просмотреть сеансы

Решетка TensorFlow (TFL)

TensorFlow Lattice - это библиотека, которая реализует гибкие, контролируемые и интерпретируемые модели на основе решеток. Библиотека позволяет вводить знания предметной области в процесс обучения с помощью здравого смысла или политически мотивированных ограничений формы . Это делается с помощью набора Keras слоев , которые могут удовлетворить такие ограничения, как монотонность, выпуклость и попарное доверие. Библиотека также предоставляет простой в настройке консервированный оценок .

Концепции

Этот раздел представляет собой упрощенную версию описания в монотонный калиброванный Интерполированное Look-Up Tables , JMLR 2016 года.

Решетки

Решетка представляет собой интерполированное справочную таблицу , которая может аппроксимировать произвольные ввода-вывода отношений в ваших данных. Он накладывает регулярную сетку на ваше входное пространство и изучает значения для выходных данных в вершинах сетки. Для контрольной точки \(x\), \(f(x)\) линейно интерполируются от решетки значений окружающих \(x\).

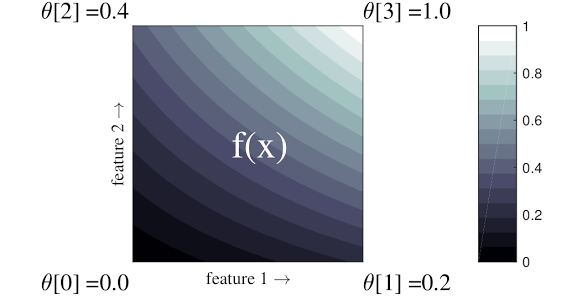
Простой пример выше , является функцией с 2 входными функциями и 4 параметров:\(\theta=[0, 0.2, 0.4, 1]\), которые являются значения работы функции в углах входного пространства; остальная часть функции интерполируется из этих параметров.

Функция \(f(x)\) может захватывать нелинейные взаимодействия между объектами. Вы можете думать о параметрах решетки как о высоте полюсов, установленных в земле на регулярной сетке, и полученная функция подобна ткани, натянутой на четыре полюса.

С \(D\) функций и 2 вершин по каждому измерению, регулярная решетка будет иметь \(2^D\) параметры. Чтобы соответствовать более гибкой функции, вы можете указать более мелкозернистую решетку по пространству признаков с большим количеством вершин по каждому измерению. Функции решеточной регрессии непрерывны и кусочно бесконечно дифференцируемы.

Калибровка

Скажем , предыдущий пример решетка представляет изученную пользователь счастье с предложенной местной кофейней , рассчитанной с помощью функции:

  • цена на кофе от 0 до 20 долларов
  • расстояние до пользователя в диапазоне от 0 до 30 километров

Мы хотим, чтобы наша модель познавала удовлетворенность пользователей с помощью предложения местной кофейни. Модели TensorFlow решетки можно использовать кусочно - линейные функции (с tfl.layers.PWLCalibration ) для калибровки и нормализуют входную функцию в диапазон принятого решеткой: от 0,0 до 1,0 в примере решетки выше. Ниже показаны примеры таких функций калибровки с 10 ключевыми точками:

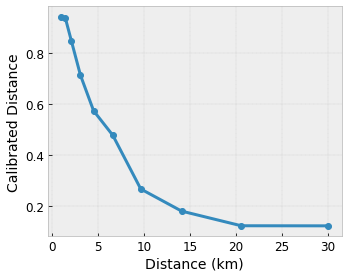
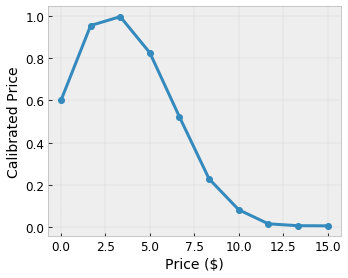
Часто бывает хорошей идеей использовать квантили функций в качестве входных ключевых точек. TensorFlow решетка консервированных оценщики могут автоматически установить входные ключевые точки к функции квантилям.

Для категориальных особенностей, TensorFlow Решетка обеспечивает категорическую калибровку (с tfl.layers.CategoricalCalibration ) с подобной продукцией , ограничивающей к корму в решетку.

Ансамбли

Число параметров слоя решетки экспоненциально увеличивается с числом входных функций, поэтому не очень хорошо масштабируется до очень больших размеров. Чтобы преодолеть это ограничение, TensorFlow Lattice предлагает ансамбли решеток , которые объединяют ( в среднем) несколько крошечных решеток, что позволяет модели линейно расти в ряд особенностей.

В библиотеке есть два варианта этих ансамблей:

  • Случайные Крошечные решетки (RTL): Каждый подмодель использует случайное подмножество функций (с заменой).

  • Кристаллы: Кристаллы алгоритм сначала тренирует prefitting модели, оценки попарных функций взаимодействия. Затем он упорядочивает окончательный ансамбль таким образом, чтобы объекты с большим количеством нелинейных взаимодействий находились в одних и тех же решетках.

Почему решетка TensorFlow?

Вы можете найти введение коротка , чтобы TensorFlow Lattice в этой TF Блог пост .

Интерпретируемость

Поскольку параметры каждого слоя являются выходными данными этого уровня, легко анализировать, понимать и отлаживать каждую часть модели.

Точные и гибкие модели

Использование мелкозернистых решеток, можно получить сколь угодно сложные функции с одним слоем решетки. Использование нескольких слоев калибраторов и решеток часто хорошо работает на практике и может соответствовать или превосходить модели DNN аналогичных размеров.

Ограничения формы здравого смысла

Данные обучения в реальном мире могут недостаточно представлять данные времени выполнения. Гибкие решения машинного обучения, такие как DNN или леса, часто действуют неожиданно и даже резко в частях входного пространства, не охваченных обучающими данными. Такое поведение особенно проблематично, когда могут быть нарушены ограничения политики или справедливости.

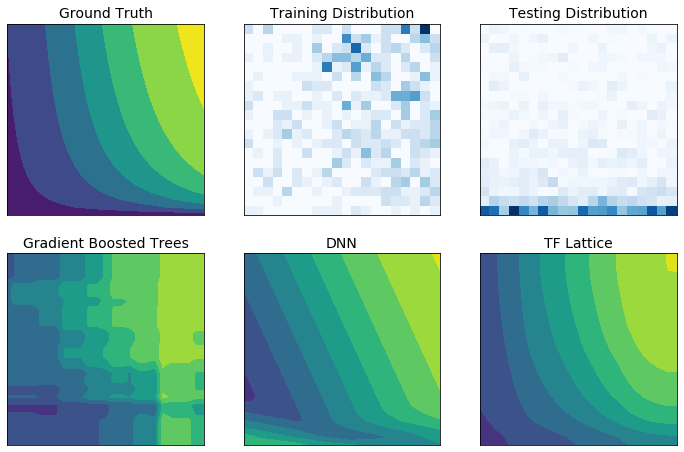
Несмотря на то, что общие формы регуляризации могут привести к более разумной экстраполяции, стандартные регуляризаторы не могут гарантировать разумное поведение модели во всем входном пространстве, особенно с входами большой размерности. Переход на более простые модели с более контролируемым и предсказуемым поведением может серьезно сказаться на точности модели.

TF Lattice позволяет продолжать использовать гибкие модели, но предлагает несколько вариантов впрыснуть знания о предметной области в процесс обучения посредством семантический значимого здравого смысла или политически мотивированных ограничений формы :

  • Монотонность: Можно указать , что выход должен только увеличиваться / уменьшаться по отношению к входу. В нашем примере вы можете указать, что увеличение расстояния до кафе должно только уменьшать прогнозируемые предпочтения пользователя.

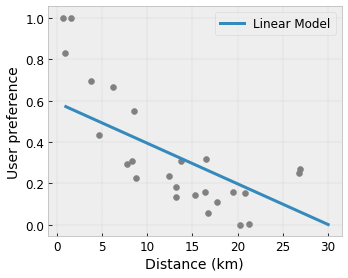
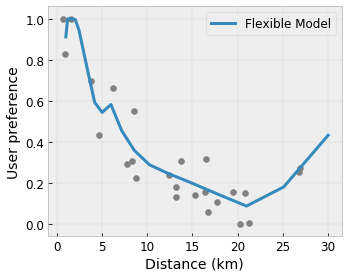
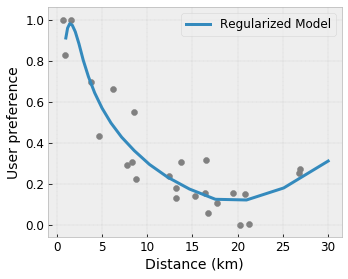
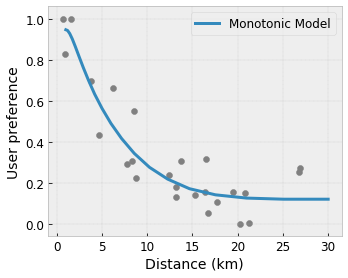
  • Выпуклость / вогнутость: Можно указать , что функция формы может быть выпуклой или вогнутой. В сочетании с монотонностью это может заставить функцию представлять убывающую отдачу по отношению к заданной функции.

  • Унимодальности: Можно указать , что функция должна иметь уникальный пик или уникальную долину. Это позволяет представлять функции , которые имеют сладкое пятно относительно функции.

  • Парное доверие: Это ограничение работает на пару функций и предполагает , что одна функции ввода семантический отражает доверие к другой функции. Например, большее количество отзывов делает вас более уверенными в среднем звездном рейтинге ресторана. Модель будет более чувствительной по отношению к рейтингу (т. Е. Будет иметь больший наклон по отношению к рейтингу), когда количество обзоров будет выше.

Контролируемая гибкость с помощью регуляризаторов

Помимо ограничений формы, решетка TensorFlow предоставляет ряд регуляризаторов для управления гибкостью и плавностью функции для каждого уровня.

  • Регуляризатор: Лапласиан Выходы решетки / калибровка вершина / ключевые точки регуляризуются по отношению к значениям соответствующих соседей. Это приводит к функции пологой.

  • Гессиан регуляризатор: Это штрафует первую производную калибровочного PWL слоя , чтобы сделать функцию более линейной.

  • Морщин регуляризатор: Это штрафует вторую производную калибровочного PWL слоя , чтобы избежать резких изменений в кривизне. Это делает функцию более плавной.

  • Торсионный регуляризатор: Выходы решетки будут регуляризованными на предотвращение кручения среди особенностей. Другими словами, модель будет упорядочена в сторону независимости между вкладом функций.

Смешивайте и сочетайте с другими слоями Keras

Вы можете использовать слои TF Lattice в сочетании с другими слоями Keras для построения частично ограниченных или регуляризованных моделей. Например, калибровочные слои решетки или PWL могут использоваться на последнем уровне более глубоких сетей, которые включают в себя вложения или другие слои Keras.

Статьи

Учебники и документация по API

Для обычных типовых архитектур, вы можете использовать модели Premade Keras или консервированных оценщик . Вы также можете создавать собственные модели с использованием TF Lattice Keras слоев или смешивать и сочетать с другими слоями Keras. Проверьте полную документацию API для деталей.