TensorFlow Lattice is a library that implements flexible, controlled and interpretable lattice based models. The library enables you to inject domain knowledge into the learning process through common-sense or policy-driven shape constraints. This is done using a collection of Keras layers that can satisfy constraints such as monotonicity, convexity and pairwise trust. The library also provides easy to setup premade models.
Concepts
This section is a simplified version of the description in Monotonic Calibrated Interpolated Look-Up Tables , JMLR 2016.
Lattices
A lattice is an interpolated look-up table that can approximate arbitrary input-output relationships in your data. It overlaps a regular grid onto your input space and learns values for the output in the vertices of the grid. For a test point \(x\), \(f(x)\) is linearly interpolated from the lattice values surrounding \(x\).
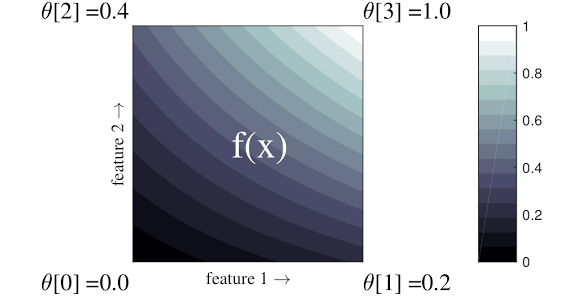
The simple example above is a function with 2 input features and 4 parameters: \(\theta=[0, 0.2, 0.4, 1]\), which are the function's values at the corners of the input space; the rest of the function is interpolated from these parameters.
The function \(f(x)\) can capture non-linear interactions between features. You can think of the lattice parameters as the height of poles set in the ground on a regular grid, and the resulting function is like cloth pulled tight against the four poles.
With \(D\) features and 2 vertices along each dimension, a regular lattice will have \(2^D\) parameters. To fit a more flexible function, you can specify a finer-grained lattice over the feature space with more vertices along each dimension. Lattice regression functions are continuous and piecewise infinitely differentiable.
Calibration
Let's say the preceding sample lattice represents a learned user happiness with a suggested local coffee shop calculated using features:
- coffee price, in range 0 to 20 dollars
- distance to the user, in range 0 to 30 kilometers
We want our model to learn user happiness with a local coffee shop suggestion.
TensorFlow Lattice models can use piecewise linear functions (with
tfl.layers.PWLCalibration) to calibrate and normalize the input features to
the range accepted by the lattice: 0.0 to 1.0 in the example lattice above. The
following show examples such calibrations functions with 10 keypoints:
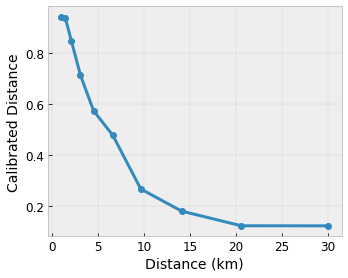
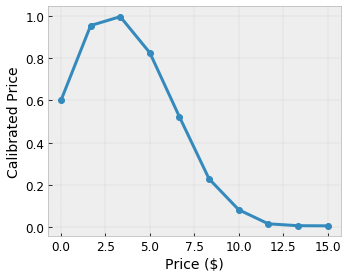
It is often a good idea to use the quantiles of the features as input keypoints. TensorFlow Lattice premade models can automatically set the input keypoints to the feature quantiles.
For categorical features, TensorFlow Lattice provides categorical calibration
(with tfl.layers.CategoricalCalibration) with similar output bounding to feed
into a lattice.
Ensembles
The number of parameters of a lattice layer increases exponentially with the number of input features, hence not scaling well to very high dimensions. To overcome this limitation, TensorFlow Lattice offers ensembles of lattices that combine (average) several tiny lattices, which enables the model to grow linearly in the number of features.
The library provides two variations of these ensembles:
Random Tiny Lattices (RTL): Each submodel uses a random subset of features (with replacement).
Crystals : The Crystals algorithm first trains a prefitting model that estimates pairwise feature interactions. It then arranges the final ensemble such that features with more non-linear interactions are in the same lattices.
Why TensorFlow Lattice ?
You can find a brief introduction to TensorFlow Lattice in this TF Blog post.
Interpretability
Since the parameters of each layer are the output of that layer, it is easy to analyze, understand and debug each part of the model.
Accurate and Flexible Models
Using fine-grained lattices, you can get arbitrarily complex functions with a single lattice layer. Using multiple layers of calibrators and lattices often work nicely in practice and can match or outperform DNN models of similar sizes.
Common-Sense Shape Constraints
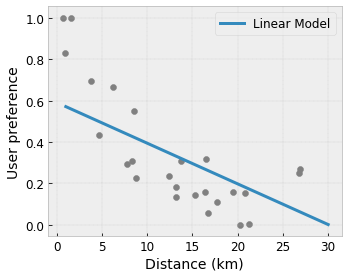
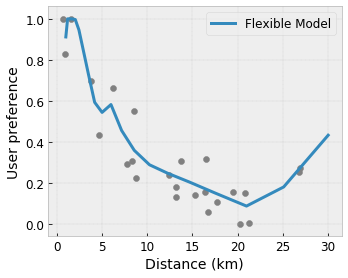
Real world training data may not sufficiently represent the run-time data. Flexible ML solutions such as DNNs or forests often act unexpectedly and even wildly in parts of the input space not covered by the training data. This behaviour is especially problematic when policy or fairness constraints can be violated.
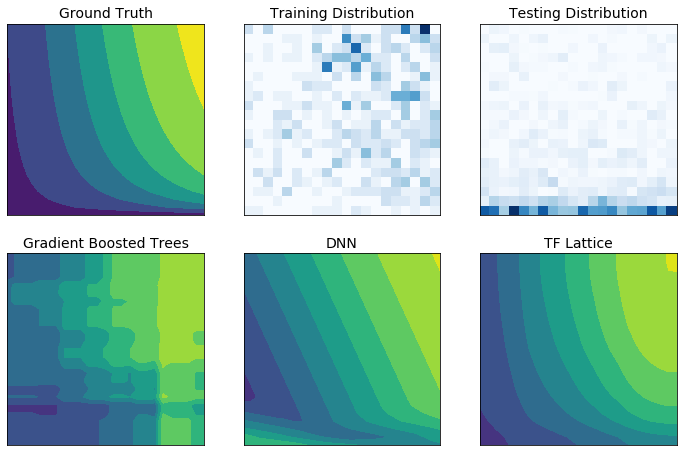
Even though common forms of regularization can result in more sensible extrapolation, standard regularizers cannot guarantee reasonable model behaviour across the entire input space, especially with high-dimensional inputs. Switching to simpler models with more controlled and predictable behaviour can come at a severe cost to the model accuracy.
TF Lattice makes it possible to keep using flexible models, but provides several options to inject domain knowledge into the learning process through semantically meaningful common-sense or policy-driven shape constraints:
- Monotonicity: You can specify that the output should only increase/decrease with respect to an input. In our example, you may want to specify that increased distance to a coffee shop should only decrease the predicted user preference.
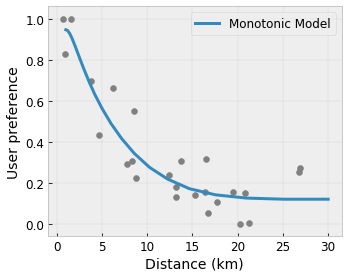
Convexity/Concavity: You can specify that the function shape can be convex or concave. Mixed with monotonicity, this can force the function to represent diminishing returns with respect to a given feature.
Unimodality: You can specify that the function should have a unique peak or unique valley. This lets you represent functions that have a sweet spot with respect to a feature.
Pairwise trust: This constraint works on a pair of features and suggests that one input feature semantically reflects trust in another feature. For example, higher number of reviews makes you more confident in the average star rating of a restaurant. The model will be more sensitive with respect to the star rating (i.e. will have a larger slope with respect to the rating) when the number of reviews is higher.
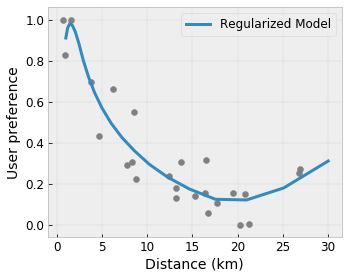
Controlled Flexibility with Regularizers
In addition to shape constraints, TensorFlow lattice provides a number of regularizers to control the flexibility and smoothness of the function for each layer.
Laplacian Regularizer: Outputs of the lattice/calibration vertices/keypoints are regularized towards the values of their respective neighbors. This results in a flatter function.
Hessian Regularizer: This penalizes the first derivative of the PWL calibration layer to make the function more linear.
Wrinkle Regularizer: This penalizes the second derivative of the PWL calibration layer to avoid sudden changes in the curvature. It makes the function smoother.
Torsion Regularizer: Outputs of the lattice will be regularized towards preventing torsion among the features. In other words, the model will be regularized towards independence between the contributions of the features.
Mix and match with other Keras layers
You can use TF Lattice layers in combination with other Keras layers to construct partially constrained or regularized models. For example, lattice or PWL calibration layers can be used at the last layer of deeper networks that include embeddings or other Keras layers.
Papers
- Deontological Ethics By Monotonicity Shape Constraints, Serena Wang, Maya Gupta, International Conference on Artificial Intelligence and Statistics (AISTATS), 2020
- Shape Constraints for Set Functions, Andrew Cotter, Maya Gupta, H. Jiang, Erez Louidor, Jim Muller, Taman Narayan, Serena Wang, Tao Zhu. International Conference on Machine Learning (ICML), 2019
- Diminishing Returns Shape Constraints for Interpretability and Regularization, Maya Gupta, Dara Bahri, Andrew Cotter, Kevin Canini, Advances in Neural Information Processing Systems (NeurIPS), 2018
- Deep Lattice Networks and Partial Monotonic Functions, Seungil You, Kevin Canini, David Ding, Jan Pfeifer, Maya R. Gupta, Advances in Neural Information Processing Systems (NeurIPS), 2017
- Fast and Flexible Monotonic Functions with Ensembles of Lattices, Mahdi Milani Fard, Kevin Canini, Andrew Cotter, Jan Pfeifer, Maya Gupta, Advances in Neural Information Processing Systems (NeurIPS), 2016
- Monotonic Calibrated Interpolated Look-Up Tables, Maya Gupta, Andrew Cotter, Jan Pfeifer, Konstantin Voevodski, Kevin Canini, Alexander Mangylov, Wojciech Moczydlowski, Alexander van Esbroeck, Journal of Machine Learning Research (JMLR), 2016
- Optimized Regression for Efficient Function Evaluation, Eric Garcia, Raman Arora, Maya R. Gupta, IEEE Transactions on Image Processing, 2012
- Lattice Regression, Eric Garcia, Maya Gupta, Advances in Neural Information Processing Systems (NeurIPS), 2009
Tutorials and API docs
For common model architectures, you can use Keras premade models. You can also create custom models using TF Lattice Keras layers or mix and match with other Keras layers. Check out the full API docs for details.
