 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запускаем в Google Colab Запускаем в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
Установить
TF_Installation = 'System'
if TF_Installation == 'TF Nightly':
!pip install -q --upgrade tf-nightly
print('Installation of `tf-nightly` complete.')
elif TF_Installation == 'TF Stable':
!pip install -q --upgrade tensorflow
print('Installation of `tensorflow` complete.')
elif TF_Installation == 'System':
pass
else:
raise ValueError('Selection Error: Please select a valid '
'installation option.')
Установить
TFP_Installation = "System"
if TFP_Installation == "Nightly":
!pip install -q tfp-nightly
print("Installation of `tfp-nightly` complete.")
elif TFP_Installation == "Stable":
!pip install -q --upgrade tensorflow-probability
print("Installation of `tensorflow-probability` complete.")
elif TFP_Installation == "System":
pass
else:
raise ValueError("Selection Error: Please select a valid "
"installation option.")
Абстрактный
В этой коллаборации мы демонстрируем, как подобрать обобщенную линейную модель со смешанными эффектами, используя вариационный вывод в TensorFlow Probability.
Модельная семья
Обобщенные линейные модели смешанных эффектов (GLM - модели) похожи на обобщенные линейные модели (GLM) за исключением того, что они включают образец специфический шум в предсказанной линейного отклика. Это полезно отчасти потому, что позволяет редко используемым функциям обмениваться информацией с более часто встречающимися функциями.
Как порождающий процесс, Обобщенная линейная модель со смешанными эффектами (GLMM) характеризуется:
\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]
где:
\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]
Другими словами, это говорит о том, что каждая категория каждой группы связана с образцом, \(\beta_{rc}\), от многомерный нормальный. Несмотря на то, \(\beta_{rc}\) рисует всегда независимы, они только распределены тождественно для группы \(r\): извещение есть ровно один \(\Sigma_r\) для каждого \(r\in\{1,\ldots,R\}\).
При аффинно в сочетании с особенностями группы в образце в (\(z_{r,i}\)), результат выборки конкретных шумы на \(i\)-м предсказанной линейный отклик (который в противном случае \(x_i^\top\omega\)).
Когда мы оцениваем \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) мы , по существу , оценивающее количество шума , случайный эффект группа несет , которые иначе бы утопить вне сигнал , присутствующие в \(x_i^\top\omega\).
Есть множество вариантов для \(\text{Distribution}\) и обратной функции связи , \(g^{-1}\). Обычные варианты:
- \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
- \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), и,
- \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).
Для получения дополнительных возможностей см tfp.glm модуль.
Вариационный вывод
К сожалению, нахождение оценок максимального правдоподобия параметров \(\beta,\{\Sigma_r\}_r^R\) влечет за собой неаналитический интеграл. Чтобы обойти эту проблему, мы вместо этого
- Определить параметризованное семейство распределений (далее «суррогатная плотность»), обозначаемый \(q_{\lambda}\) в приложении.
- Найти параметры \(\lambda\) так что \(q_{\lambda}\) близка к нашей истинной цели denstiy.
Семейство распределений будет независимым от Гаусса , соответствующих размеров, а также от «близко к нашей целевой плотности», мы будем называть «минимизацией дивергенции Кульбаки-Либлер ». Смотрите, например , раздел 2.2 «вариационные умозаключения: обзор для статистиков» для хорошо написанного вывода и мотивации. В частности, это показывает, что минимизация расхождения KL эквивалентна минимизации нижней границы отрицательного свидетельства (ELBO).
Игрушечная проблема
Гельман и др. (2007) «радон набора данных» является набором данных иногда используется для демонстрации подходов к регрессии. (Например, это тесно связанно сообщение PyMC3 блог .) Радон набор данные содержит закрытое измерение радона , принятое на всей территории Соединенных Штатов. Радон естественно ocurring радиоактивный газ , который является токсичным в высоких концентрациях.
Для нашей демонстрации предположим, что мы заинтересованы в подтверждении гипотезы о том, что уровни радона выше в домохозяйствах, содержащих подвал. Мы также подозреваем, что концентрация радона связана с типом почвы, то есть с географией.
Чтобы обозначить это как проблему ML, мы попытаемся предсказать уровни логарифмического радона на основе линейной функции пола, на котором были сняты показания. Мы также будем использовать округ в качестве случайного эффекта и при этом учитывать различия, связанные с географическим положением. Другими словами, мы будем использовать обобщенную линейную модель смешанного эффекта .
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import os
from six.moves import urllib
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
Мы также сделаем быструю проверку наличия графического процессора:
if tf.test.gpu_device_name() != '/device:GPU:0':
print("We'll just use the CPU for this run.")
else:
print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))
We'll just use the CPU for this run.
Получить набор данных:
Мы загружаем набор данных из наборов данных TensorFlow и делаем небольшую предварительную обработку.
def load_and_preprocess_radon_dataset(state='MN'):
"""Load the Radon dataset from TensorFlow Datasets and preprocess it.
Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
to Minnesota data and preprocess to obtain the following features:
- `county`: Name of county in which the measurement was taken.
- `floor`: Floor of house (0 for basement, 1 for first floor) on which the
measurement was taken.
The target variable is `log_radon`, the log of the Radon measurement in the
house.
"""
ds = tfds.load('radon', split='train')
radon_data = tfds.as_dataframe(ds)
radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
df = radon_data[radon_data.state==state.encode()].copy()
df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
# Make county names look nice.
df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
# Remap categories to start from 0 and end at max(category).
df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
df['county_code'] = df.county.cat.codes
# Radon levels are all positive, but log levels are unconstrained
df['log_radon'] = df['radon'].apply(np.log)
# Drop columns we won't use and tidy the index
columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
df = df[columns_to_keep].reset_index(drop=True)
return df
df = load_and_preprocess_radon_dataset()
df.head()
Специализация семейства GLMM
В этом разделе мы специализируем семейство GLMM на задаче прогнозирования уровней радона. Для этого сначала рассмотрим специальный случай GLMM с фиксированным эффектом:
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]
Эта модель утверждает , что журнал радон в смотровую \(j\) является (в ожидании) , управляемые с пола на \(j\)- е чтение берется на плюс некоторая константа перехватывать. В псевдокоде мы могли бы написать
def estimate_log_radon(floor):
return intercept + floor_effect[floor]
есть масса уроков для каждого этажа и универсального intercept срок. Глядя на измерения радона с этажей 0 и 1, похоже, что это может быть хорошим началом:
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')
df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");
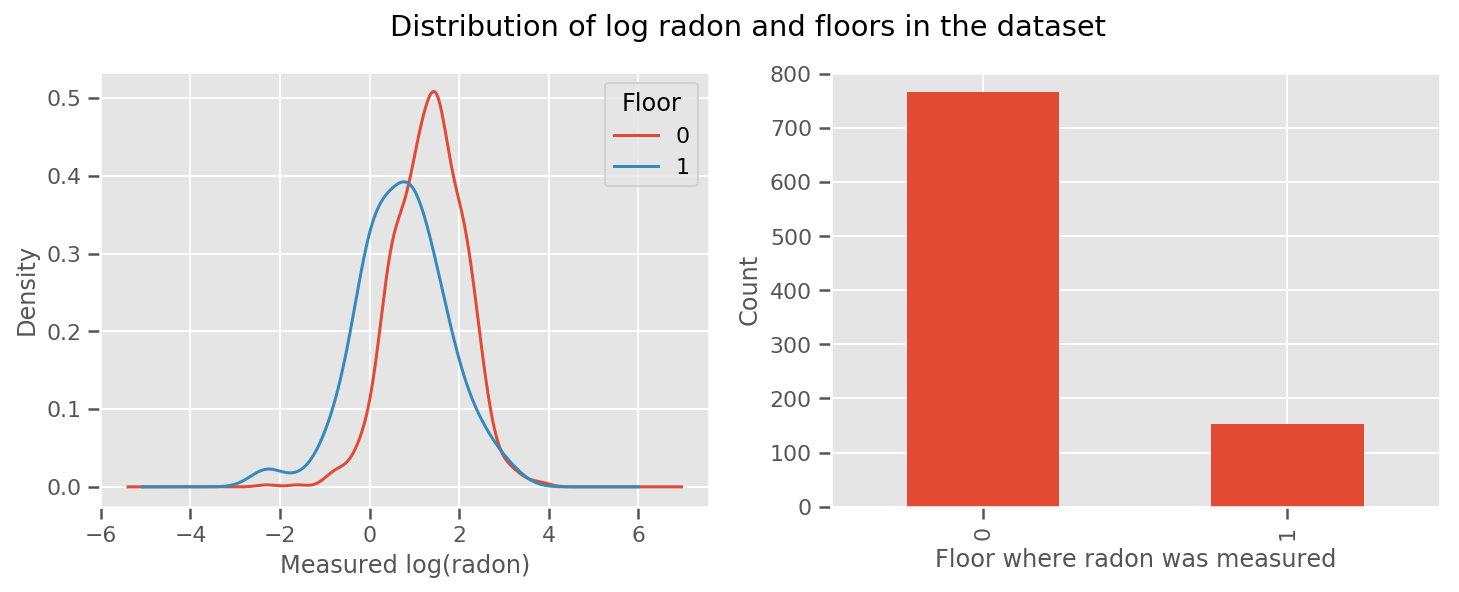
Возможно, даже лучше сделать модель немного более сложной, включая кое-что о географии: радон является частью цепочки распада урана, который может присутствовать в земле, поэтому географическое положение кажется ключевым для объяснения.
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]
Опять же, в псевдокоде мы имеем
def estimate_log_radon(floor, county):
return intercept + floor_effect[floor] + county_effect[county]
то же самое, что и раньше, за исключением веса конкретного округа.
Учитывая достаточно большой обучающий набор, это разумная модель. Однако, учитывая наши данные из Миннесоты, мы видим, что существует большое количество округов с небольшим количеством измерений. Например, в 39 округах из 85 имеется менее пяти наблюдений.
Это мотивирует обмен статистической силой между всеми нашими наблюдениями таким образом, чтобы сходиться к вышеупомянутой модели по мере увеличения количества наблюдений на округ.
fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');
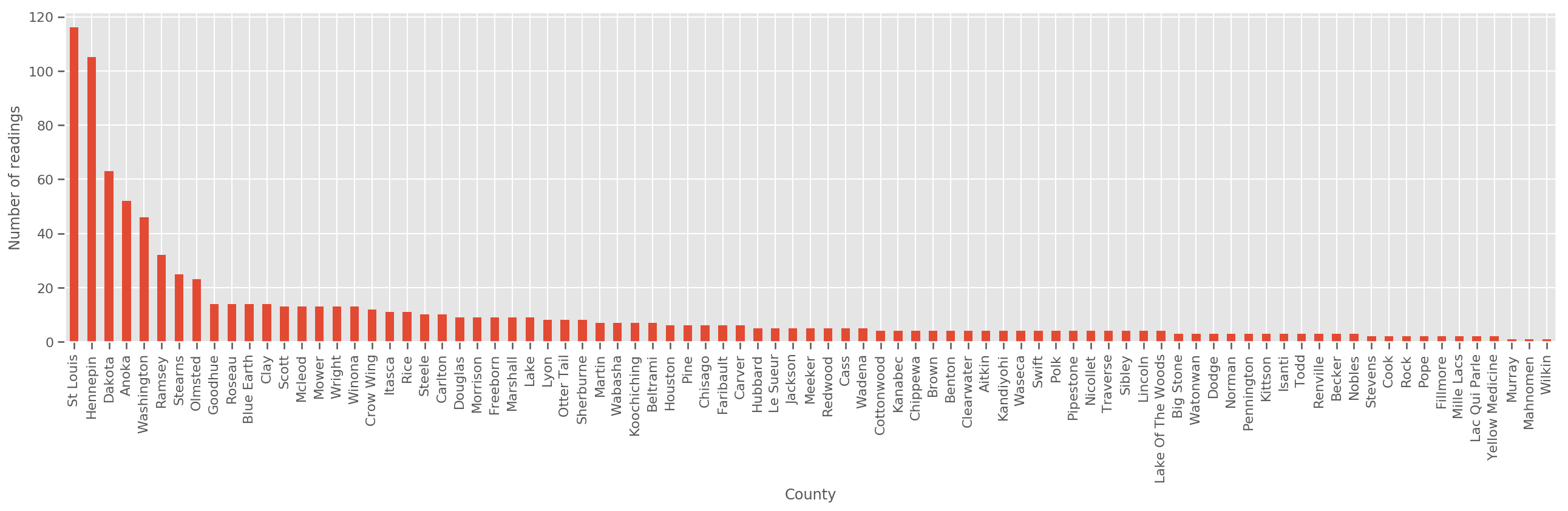
Если мы вписываемся эта модель, то county_effect вектор, скорее всего , в конечном итоге запоминание результатов для стран , которые имели лишь несколько примеров обучения, возможно , переобучение и приводя к плохому обобщению.
GLMM предлагает счастливую середину двух вышеупомянутых GLM. Мы могли бы подумать о том, чтобы
\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]
Эта модель является такой же , как первый, но мы зафиксировали нашу вероятность быть нормальное распределение, и разделит дисперсию во всех округах через (один) переменной county_scale . В псевдокоде
def estimate_log_radon(floor, county):
county_mean = county_effect[county]
random_effect = np.random.normal() * county_scale + county_mean
return intercept + floor_effect[floor] + random_effect
Мы будем выводить совместное распределение по county_scale , county_mean , и random_effect используя наши наблюдаемые данные. Глобальная county_scale позволяет разделить статистическую силу по уездам: те , с большим количеством наблюдений обеспечивает попадание в дисперсии графств с несколькими наблюдениями. Кроме того, по мере того, как мы собираем больше данных, эта модель будет сходиться к модели без объединенной масштабной переменной - даже с этим набором данных мы придем к аналогичным выводам о наиболее наблюдаемых округах с помощью любой из моделей.
Эксперимент
Теперь мы попытаемся подогнать приведенную выше GLMM, используя вариационный вывод в TensorFlow. Сначала мы разделим данные на функции и метки.
features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()
Укажите модель
def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):
def model():
county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
scale=county_scale,
name='county_prior')
random_effect = tf.gather(county_prior, county, axis=-1)
fixed_effect = intercept + floor_weight * floor
linear_response = fixed_effect + random_effect
yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
return tfd.JointDistributionCoroutineAutoBatched(model)
joint = make_joint_distribution_coroutine(
features.floor.values, features.county_code.values, df.county.nunique(),
df.floor.nunique())
# Define a closure over the joint distribution
# to condition on the observed labels.
def target_log_prob_fn(*args):
return joint.log_prob(*args, likelihood=labels)
Укажите суррогатный задний
Теперь мы собрали суррогатную семью \(q_{\lambda}\), где параметры \(\lambda\) являются обучаемыми. В этом случае, наша семья независимые многомерные нормальные распределения, один для каждого параметра, и \(\lambda = \{(\mu_j, \sigma_j)\}\), где \(j\) индексирует четыре параметра.
Метод , который мы используем , чтобы соответствовать суррогатной семье использует tf.Variables . Мы также используем tfp.util.TransformedVariable наряду с Softplus , чтобы ограничить параметры (обучаемый) масштаба , чтобы быть положительным. Кроме того, мы применяем Softplus ко всему scale_prior , что является положительным параметром.
Мы инициализируем эти обучаемые переменные с небольшим дрожанием, чтобы помочь в оптимизации.
# Initialize locations and scales randomly with `tf.Variable`s and
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
bijector=tfb.Softplus())
n_counties = df.county.nunique()
surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())), # scale_prior
tfd.Normal(_init_loc(), _init_scale()), # intercept
tfd.Normal(_init_loc(), _init_scale()), # floor_weight
tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))]) # county_prior
Обратите внимание , что эта клетка может быть заменены tfp.experimental.vi.build_factored_surrogate_posterior , как:
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=joint.event_shape_tensor()[:-1],
constraining_bijectors=[tfb.Softplus(), None, None, None])
Результаты
Напомним, что наша цель - определить управляемое параметризованное семейство распределений, а затем выбрать параметры так, чтобы у нас было управляемое распределение, близкое к нашему целевому распределению.
Мы построили распределение суррогатного выше, и можем использовать tfp.vi.fit_surrogate_posterior , который принимает оптимизатор и заданное число шагов , чтобы найти параметры модели суррогатной минимизации негативного ELBO (который corresonds к минимуму расхождения Кульбака-Либлер между суррогат и целевое распределение).
Возвращаемое значение является отрицательным ELBO на каждом шаге, и распределения в surrogate_posterior будут обновлены параметры найдены оптимизатором.
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
losses = tfp.vi.fit_surrogate_posterior(
target_log_prob_fn,
surrogate_posterior,
optimizer=optimizer,
num_steps=3000,
seed=42,
sample_size=2)
(scale_prior_,
intercept_,
floor_weight_,
county_weights_), _ = surrogate_posterior.sample_distributions()
print(' intercept (mean): ', intercept_.mean())
print(' floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))
intercept (mean): tf.Tensor(1.4352839, shape=(), dtype=float32)
floor_weight (mean): tf.Tensor(-0.6701997, shape=(), dtype=float32)
scale_prior (approx. mean): tf.Tensor(0.28682157, shape=(), dtype=float32)
fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
ylabel="Loss (ELBO)",
title="Loss during training",
ylim=0);
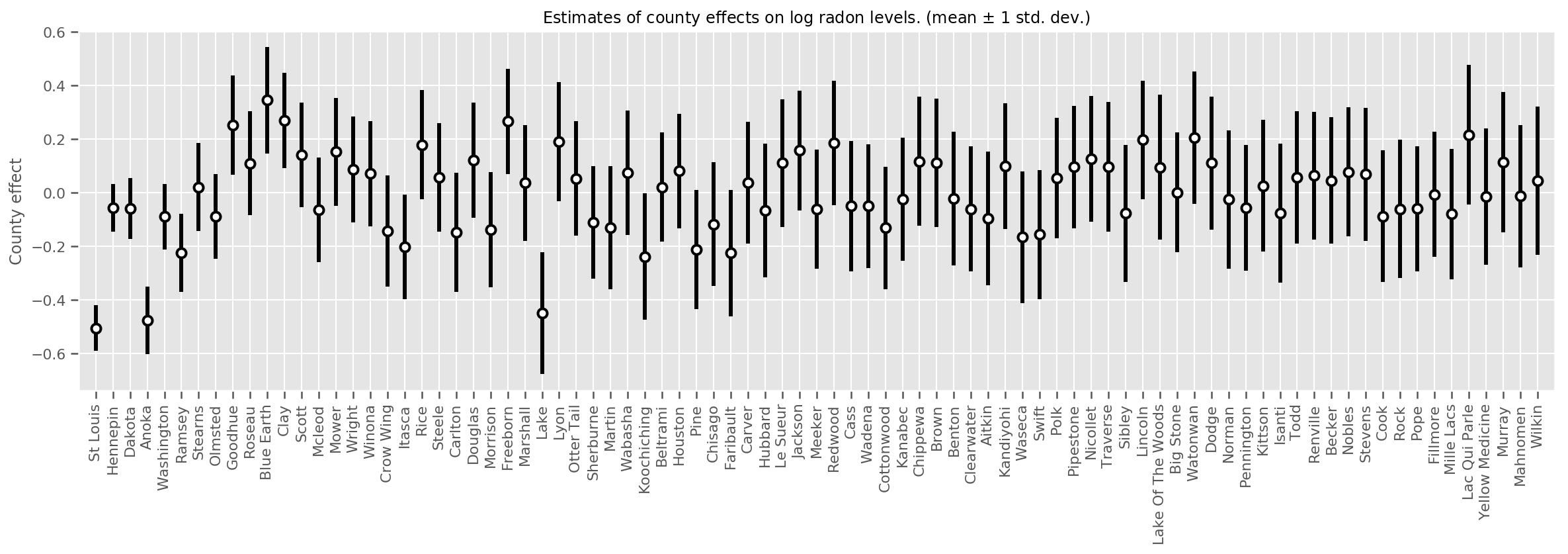
Мы можем нанести на график оценочные средние эффекты округа вместе с неопределенностью этого среднего. Мы упорядочили это по количеству наблюдений, самое большое слева. Обратите внимание, что неопределенность мала для округов с большим количеством наблюдений, но больше для округов, в которых есть только одно или два наблюдения.
county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
.agg('size')
.sort_values(ascending=False)
.reset_index(name='count'))
means = county_weights_.mean()
stds = county_weights_.stddev()
fig, ax = plt.subplots(figsize=(20, 5))
for idx, row in county_counts.iterrows():
mid = means[row.county_code]
std = stds[row.county_code]
ax.vlines(idx, mid - std, mid + std, linewidth=3)
ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)
ax.set(
xticks=np.arange(len(county_counts)),
xlim=(-1, len(county_counts)),
ylabel="County effect",
title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);
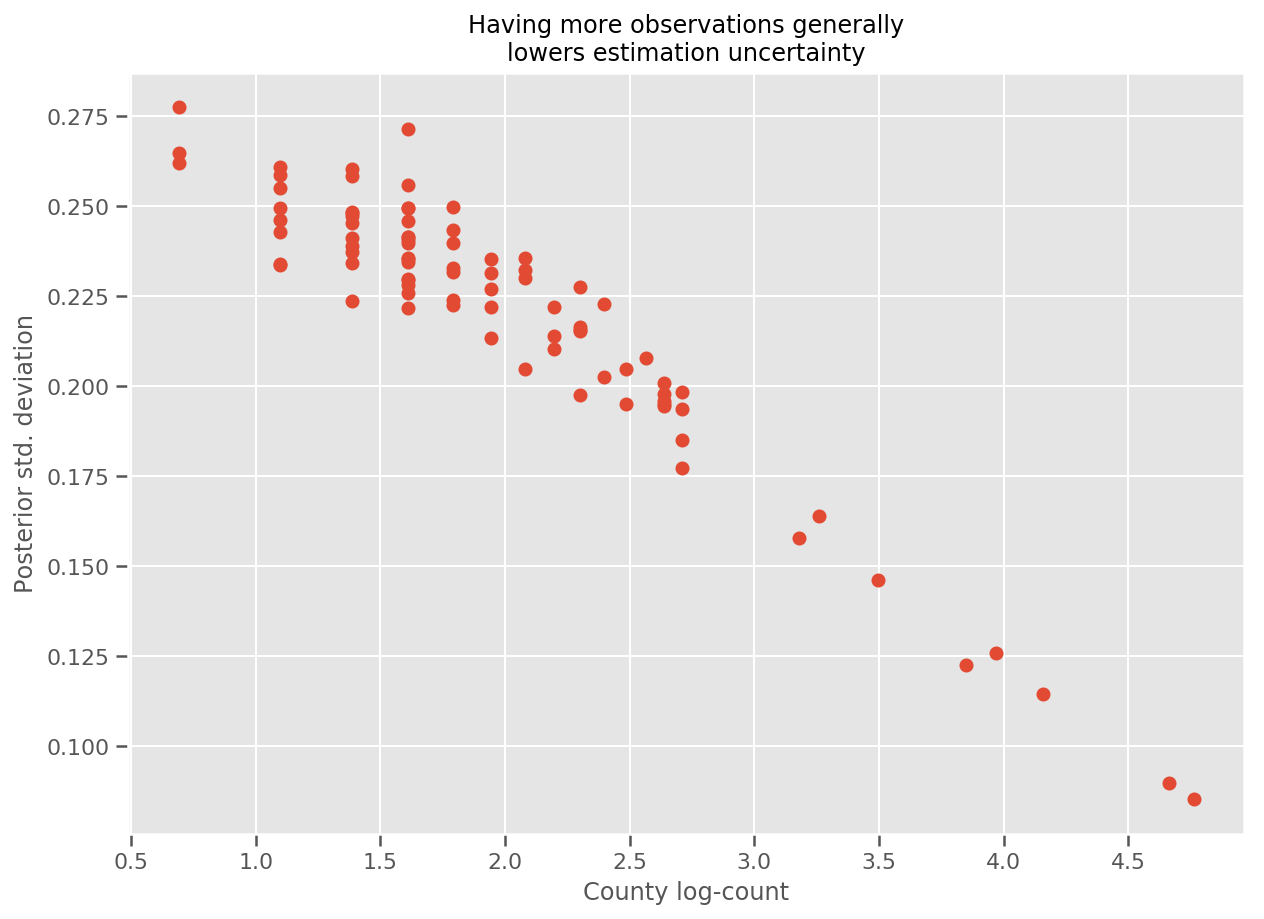
В самом деле, мы можем увидеть это более прямо, построив график логарифмического числа наблюдений против оцененного стандартного отклонения, и увидим, что зависимость является приблизительно линейной.
fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
ylabel='Posterior std. deviation',
xlabel='County log-count',
title='Having more observations generally\nlowers estimation uncertainty'
);
По сравнению с lme4 в R
%%shell
exit # Trick to make this block not execute.
radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)
# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit
# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
# Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
# Groups Name Std.Dev.
# county (Intercept) 0.3282
# Residual 0.7556
# Number of obs: 919, groups: county, 85
# Fixed Effects:
# (Intercept) floor
# 1.462 -0.693
<IPython.core.display.Javascript at 0x7f90b888e9b0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90bce1dfd0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780>
В следующей таблице приведены результаты.
print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
index=['lme4', 'vi']))
intercept floor scale lme4 1.462000 -0.6930 0.328200 vi 1.435284 -0.6702 0.287251
Эта таблица показывает , что VI результаты находятся в пределах ~ 10% lme4 «с. Это несколько удивительно, поскольку:
-
lme4основан на методе Лапласа (не VI) - в этом колабе не было предпринято никаких усилий, чтобы на самом деле сойтись,
- минимальные усилия по настройке гиперпараметров,
- не было предпринято никаких усилий для упорядочения или предварительной обработки данных (например, центральных элементов и т. д.).
Вывод
В этой колабе мы описали обобщенные линейные модели со смешанными эффектами и показали, как использовать вариационный вывод для их соответствия с помощью TensorFlow Probability. Хотя в задаче с игрушкой было всего несколько сотен обучающих выборок, используемые здесь методы идентичны тому, что необходимо в масштабе.

