تنسيق "تقسيم الشاشة حسب عدد المشاركين"

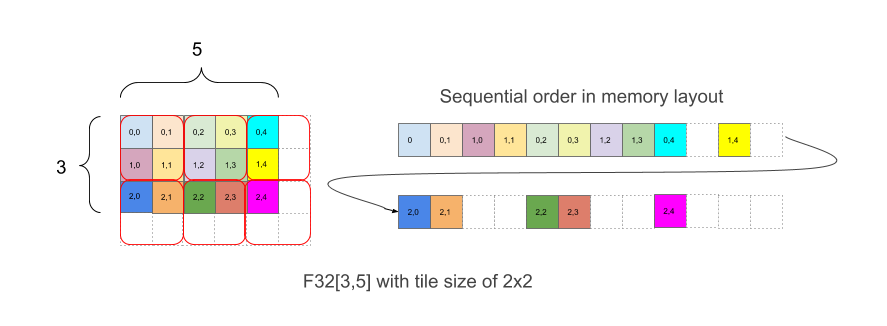
الشكل 1

يوضح الشكل 1 كيفية وضع صفيفة F32 [3,5] في الذاكرة من خلال تجانب 2×2. تتم كتابة الشكل بهذا التنسيق على النحو التالي F32[3,5]{1,0:T(2,2)}، حيث يشير الرقم 1,0 إلى الترتيب الفعلي للأبعاد (حقل minor_to_major في التنسيق) بينما يشير (2,2) بعد النقطتين الرأسيتين إلى تجانب الأبعاد المادية في مربع 2×2.

بشكل بديهي، يتم وضع المربّعات لتغطية الشكل، ثم داخل كل مربّع، يتم وضع العناصر بدون تجانب، كما في المثال أعلاه، حيث يُظهر الجزء الأيمن من المثال التنسيق في الذاكرة، بما في ذلك عناصر المساحة المتروكة البيضاء التي تمت إضافتها للحصول على مربّعات 2×2 كاملة على الرغم من أن حدود الصفيف الأصلية ليست متساوية.

لا يُشترط أن تحتوي العناصر الإضافية في المساحة المتروكة على أي قيمة معينة.

صيغ الفهرس الخطي للتجانب باستخدام شكل ومربّع

بدون التجانب، يتم تحديد العنصر e=(e_n, e_n-1, ... , e₁) في مصفوفة بحدود الصفيف d=(d_n, d_n-1, ... , d₁) (السمة الأصغر) (d1 هو البُعد الأصغر) حسب الترتيب الثانوي في الموضع:

line_index(e, d)
= line_index((e_n, e_n-1, ... , e₁), (d_n, d_n-1, ... , d₁))
= e_nd_n-1...d₁ + e_n-1 + e_n-1

لتبسيط الترميز في هذا المستند، نفترض أن أحد المربعات له نفس عدد أبعاد الصفيفة. عند تنفيذ نمط التجانب في XLA، يتم تعميمه على العناصر المتجانبة ذات الأبعاد الأقل من خلال ترك الأبعاد الأولية الأكثر أبعادًا بدون تغيير وتطبيقها فقط على الأبعاد الأصغر حجمًا، بحيث يشير المربّع المحدّد إلى لاحقة الأبعاد المادية للشكل الذي يتم تقسيمه إلى أجزاء.

عند استخدام تجانب الحجم (t_n, t_n-1, ... , t₁) يتم تعيين عنصر في الصفيف ذي الفهارس (e_n, e_n-1, ... , e₁) بهذا الموضع في التنسيق النهائي:

(⌈d/with_tile(e, ⌋, t) ⌋, coltile(e, d, t)
= معقولة_index((⌊e/t⌋, e mod t), (⌈d/t⌉, t)) (arithmetic is ⌋, ⌋, coltile(e, d, t)
= LINE_index((⌊e/t⌋, e mod t), (⌈d/t⌉, t)) (arithmetic is ⌋, ⌋, →e ⌋, راغبـ
_n

ويمكن اعتبار التنسيق مؤلفًا من جزأين: (⌊e_n/t_n⌋, ... , ⌊e₁/t₁⌋), والذي يتجاوب مع فهرس مربّعات في مصفوفة من المربّعات بالحجم (⌈d_n/t_n/t_n⌋, ... , ⌊e₁/t₁⌋), والذي يتجاوب مع فهرس مربّعات في مصفوفة من المربّعات بحجم (⌈d_n/t_n/t_n⌋, ... , /n الإجراء 1 (;mod1. ),/mod1., تظهر دالة ceil في ⌈d_i/t_i⌉ لأنه إذا تخطت المربّعات حدود الصفيف الأكبر، يتم إدراج المساحة المتروكة كما في الشكل 1. يتم وضع كل من البلاط والعناصر الموجودة داخل البلاط بشكل متكرر دون تجانب.

على سبيل المثال في الشكل 1، يحتوي العنصر (2,3) على فهرس التجانب (1,1)، وفهرس داخل التجانب (0,1)، لمتجه إحداثي مدمج هو (1,1,0,1). تحتوي فهارس المربعات فإن الفهرس الخطي مع مربع للعنصر الذي يحتوي على الفهرس (2,3) في الشكل المنطقي هو

inline_index_with_tile((2,3), (3,5), (2,2))
= line_index((1,1,0,1), (2,3,2,2))
= inline_index((1,1), (2, 4) ∙
= line_index((1,1,0,1), (2,3,2,2))
= معقولة_index((1,1), (2, 4) ∙ 4+

تجانب كإعادة شكل الحشوة وتبديل موضعها

يعمل التنسيق المستند إلى التجانب على النحو التالي:
فكِّر في مجموعة من الأبعاد (d_n ، d_n-1 ، ... ، d1) (d1 هو البُعد الأصغر). عند تنسيقه مع تقسيم الحجم إلى أجزاء (t_n, t_n-1, ... , t₁) (السمة الأصغر حجمًا هي ₁)، يمكن وصف ذلك التجانب من حيث إعادة شكل اللوحة كما يلي.

1. تمت إضافة مساحة للمصفوفة إلى (⌈d_n/t_n⌉∙t_n, ... , ⌈d₁/t₁⌉∙t₁).
2. يتم تقسيم كل بُعد i إلى (⌈d_i/ti⌉, t_i)، أي تتم إعادة تشكيل الصفيف إلى
   (⌈d_n/t_n⌉, t_n, ... , ⌈d₁/t₁⌉, t₁).
   لا يتم إجراء أي تغيير مادي على التصميم في هذه الصيغة الجديدة في حد ذاتها، لذا إنّ هذا التعديل عبارة عن بث رقمي للبيانات. إذا لم يفكر المرء بشكل صريح في التجانب، فإن إعادة الشكل هذه يمكن أن تعبر عن أي شكل بنفس عدد العناصر مثل الشكل المبطّن - المثال هنا هو كيفية التعبير عن المربع بهذه الطريقة.
3. وتحدث عملية التبديل من خلال نقل _n ، ... ، t ₁ إلى معظم الأبعاد الثانوية مع الحفاظ على ترتيبها النسبي، بحيث يصبح ترتيب الأبعاد من الأكبر إلى الأصغر حجمًا
   (⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉, t_n, _n.

يحتوي الشكل النهائي على البادئة
(⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉)، التي تصف عدد المربّعات في كل بُعد. يتم تعيين عنصر في الصفيف (e_n, ... , e₁) لهذا العنصر في الشكل النهائي:
(⌊e_n/t_n⌋, ... , ⌊e₀/t₀⌋, e_n mod t_n, ... , e₁ ). من السهل أن نرى أن الفهرس الخطي للعنصر يتبع المعادلة أعلاه كما هو متوقع.

تجانب متكرّر

يصبح تجانب XLA أكثر مرونة من خلال تطبيقه بشكل متكرر.

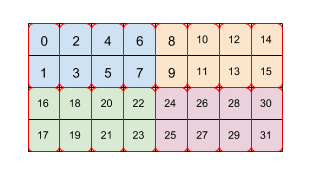
الشكل 2

يوضح الشكل 2 كيف يتم تجانب صفيف بحجم 4×8 بمستويَين من التجانب (أولاً 2×4 ثم 2×1). ونمثل هذا التجانب المتكرر كـ (2,4)(2,1). يشير كل لون إلى مربع 2×4 وكل مربع حد أحمر هو مربع 2×1. تشير الأرقام إلى الفهرس الخطي في ذاكرة هذا العنصر بتنسيق التجانب. ويتطابق هذا التنسيق مع التنسيق المستخدَم لـ BF16 على TPU، باستثناء أن المربع الأولي أكبر، تحديدًا التجانب (8,128)(2,1)، حيث يكون الغرض من التجانب الثاني بمقدار 2x1 هو جمع قيمتين من 16 بت معًا لتكوين قيمة واحدة 32 بت بطريقة تتوافق مع بنية TPU.

تجدر الإشارة إلى أنّ المربّع الثاني أو الأحدث يمكن أن يشير إلى كلٍّ من أبعاد المربعات الثانوية التي تُعيد ترتيب البيانات داخل المربّع، كما في هذا المثال باستخدام (8,128)(2,1) (2,1)، ولكن يمكن أن تشير أيضًا إلى الأبعاد الرئيسية المتقاطعة من التجانب السابق.

دمج السمات باستخدام المربّعات

يدعم تجانب XLA أيضًا دمج الأبعاد. على سبيل المثال، يمكن دمج أبعاد في F32[2,7,8,11,10]{4,3,2,1,0} في F32[112,110]{1,0} أولاً قبل تقسيمها بـ (2,3). والمربّع المستخدم هو (engagement,씨,2,googleapps,3). هنا علامة النجمة في أحد المربعات، تشير إلى أخذ هذا البعد ودمجه مع البُعد الثانوي التالي. يمكن ضم الأبعاد المتجاورة المتعددة معًا في بُعد واحد. يتم تمثيل البُعد الفرعي بقيمة -1 في بُعد المربّع، وهو ما غير صالح في أي مربّع كحجم بُعد.

وبتعبير أدق، إذا تم التخلص من البعد i من الشكل من خلال علامة النجمة في المربّع، فقبل تطبيق التعريف السابق للتجانب، تتم إزالة ذلك البعد من كل من الشكل المتجانب والمتجهات المتجانبة، وما كان البعد i-1 للشكل قد ازداد حد الصفيف من d_i-1 إلى d_id_i-1. يتم تكرار هذه الخطوة لكل علامة نجمية في متجه المربع.