Cette page a été traduite par l'API Cloud Translation.

Disposition en mosaïque

Attention :La mise en page en mosaïque est une version préliminaire qui décrit son fonctionnement. Les erreurs peuvent être ignorées en mode silencieux.

Figure 1

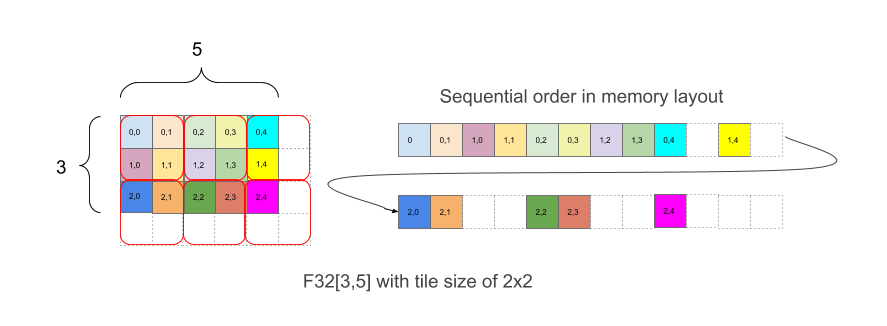
La figure 1 montre la disposition en mémoire d'un tableau F32[3,5] avec une disposition en mosaïque 2x2. Une forme avec cette mise en page s'écrit F32[3,5]{1,0:T(2,2)}, où 1,0 correspond à l'ordre physique des dimensions (champ minor_to_major dans Layout) tandis que (2,2) après le deux-points indique le mosaïque des dimensions physiques par une tuile 2x2.

Intuitivement, les tuiles sont disposées pour couvrir la forme, puis au sein de chaque tuile, les éléments sont ensuite disposés sans mosaïque, comme dans l'exemple ci-dessus, où la partie droite de l'exemple montre la mise en page en mémoire, y compris les éléments de marge intérieure blancs ajoutés pour obtenir des tuiles complètes de 2x2, même si les limites du tableau d'origine ne sont pas égales.

Les éléments supplémentaires de la marge intérieure ne doivent pas nécessairement contenir une valeur particulière.

Formules d'index linéaire pour la tuile en fonction d'une forme et d'une tuile

Sans mosaïque, un élément e=(e_n, e_n-1, ... , e₁) dans un tableau avec les limites de tableau d=(d_n, d_n-1, ... , d₁) (d1 est la dimension la plus mineure) est réparti par ordre majeur/mineur à la position:

linear_index(e, d)
= linear_index((e_n, e_n-1, ... , e₁), (d_n, d_n-1, ... , d₁))
= e_nd_n-1...d₁ + _n-2...d₁ + _n-2 ... d_n+

Pour simplifier la notation dans ce document, nous supposons qu'une carte a le même nombre de dimensions que le tableau. Dans l'implémentation du tuile de XLA, cette méthode est généralisée aux tuiles ayant moins de dimensions en laissant inchangées les dimensions initiales les plus importantes et en appliquant le carrelage uniquement aux dimensions les plus mineures, de sorte que le carrelage spécifié mentionne un suffixe des dimensions physiques de la forme en mosaïque.

Lorsque vous utilisez un carrelage de taille (t_n, t_n-1, ... , t₁), un élément du tableau avec des index (_e, e_n-1, ..., e₁) est mappé à cette position dans la mise en page finale:

<ph type="<ph-lin-2-<br-et-bi-<br-et-et-bi-et-<ph-la-classe-1-ph-li-ph<ph-la-classe-1-ph-et-lin-t-ph<ph-la-classe-1-ph-li-ph<ph-la-classe-1-ph-lin-2-0

_n

La mise en page peut être considérée comme ayant deux parties : (⌊e_n/t_n⌋, ... , ⌊e₁/t₁⌋), qui correspond à un index de carte dans un tableau de tuiles de taille (⌈d_n/t_n⌉, ... , ⌊e₁/t₁⌋), qui correspond à un index de carte dans un tableau de tuiles de taille (⌈d_n/t_n⌉, ... , ≌, 1,_{) La fonction "ceil" apparaît dans ⌈d_i/t_i⌉, car si des tuiles dépassent les limites du tableau le plus large, une marge intérieure est insérée, comme illustré dans la figure 1. Les tuiles et les éléments des tuiles sont disposés de manière récursive, sans mosaïque.}

Pour l'exemple de la figure 1, l'élément (2,3) possède un index de carte (1,1) et un index au sein de la carte (0,1), pour un vecteur de coordonnées combiné de (1,1,0,1). Les index de carte ont des limites (2,3) et la carte elle-même est (2,2) pour un vecteur combiné de (2,3,2,2). L'index linéaire avec la carte de l'élément dont l'indice (2,3) a la forme logique est alors

linear_index_with_tile((2,3), (3,5), (2,2))
= linear_index((1,1,0,1), (2,3,2,2))
= linear_index((1,1), (2,3)) ∙ 2 ∙ 2 + ∙ 2 + linear_index(= (0, 1) = (0,2) )

Mosaïque en tant que remodelage de pads/transpose

La mise en page basée sur des emplacements fonctionne comme suit:
Envisagez un tableau de dimensions (d_n, d_n-1, ... , d1) (d1 est la dimension la plus mineure). Lorsqu'il est disposé avec un carrelage de taille (t_n, t_n-1, ... , t₁) (t₁ est la dimension la plus mineure), ce carrelage peut être décrit en termes de remodelage de pads/transpose de la manière suivante.

Le tableau est complété jusqu'à (⌈d_n/t_n⌉∙t_n, ... , ⌈d₁/t₁⌉∙t₁).
Chaque dimension i est divisée en (⌈d_i/ti⌉, t_i), c'est-à-dire que le tableau est remodelé en
(⌈d_n/t_n⌉, t_n, ... , ⌈d₁/t₁⌉, t₁).
La mise en page physique n'est pas modifiée dans cette remodelage. Cette modification est donc un bitcast. Si l'on ne pense pas explicitement à un carrelage, cette reforme peut exprimer n'importe quelle forme avec le même nombre d'éléments que la forme remplie. Cet exemple montre comment exprimer une carte de cette manière.
Pour effectuer une transposition, on déplace t_n, ... , t₁ vers les dimensions les plus mineures, tout en conservant leur ordre relatif, de sorte que l'ordre des dimensions, de la plus grande à la plus mineure, devienne
(⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉, t_n, t).

La forme finale a le préfixe
(⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉), qui décrit le nombre de tuiles dans chaque dimension. Un élément du tableau (e_n, ... , e₁) est mappé à cet élément dans sa forme finale:
(⌊e_n/t_n⌋, ... , ⌊e₀/t₀⌋, e_n mod t_n, ... , t₁). Il est facile de voir que l'indice linéaire de l'élément suit la formule ci-dessus, comme prévu.

Mosaïque répété

Le carrelage de XLA devient encore plus flexible en l'appliquant à plusieurs reprises.

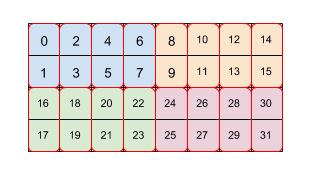
Figure 2

La figure 2 montre comment un tableau de taille 4 x 8 est organisé en mosaïque selon deux niveaux de tuiles (d'abord 2 x 4, puis 2 x 1). Nous représentons ce mosaïque répété comme (2,4)(2,1). Chaque couleur correspond à une tuile 2x4, et chaque bordure rouge est une tuile 2x1. Les nombres indiquent l'index linéaire en mémoire de cet élément au format en mosaïque. Ce format correspond au format utilisé pour BF16 sur TPU, si ce n'est que la tuile initiale est plus grande, à savoir que la tuile est (8,128)(2,1), où l'objectif de la deuxième mise en mosaïque par 2x1 est de collecter deux valeurs de 16 bits pour former une valeur 32 bits d'une manière qui s'aligne sur l'architecture d'un TPU.

Notez qu'une deuxième tuile ou ultérieure peut faire référence aux deux dimensions mineures dans la carte, ce qui réorganise simplement les données à l'intérieur de la carte, comme dans cet exemple avec (8,128)(2,1), mais peut également faire référence aux principales dimensions de tuiles croisées de la mosaïque précédente.

Combiner des dimensions à l'aide de tuiles

Le tuilage de XLA permet également de combiner des dimensions. Par exemple, il peut combiner les dimensions de F32[2,7,8,11,10]{4,3,2,1,0} dans F32[112,110]{1,0} d'abord avant de la tuer avec (2,3). La vignette utilisée est (∗,∗,2,∗,3). Ici, un astérisque dans une carte implique de prendre cette dimension et de la combiner avec la dimension suivante la plus mineure. Plusieurs dimensions adjacentes peuvent être subsumées en une seule dimension. Une dimension sous-sommée est représentée par une valeur de tuile de -1 dans cette dimension de la carte, ce qui n'est pas valide dans une carte en tant que taille de dimension.

Plus précisément, si la dimension i de la forme est éliminée via un astérisque dans la carte, alors avant l'application de la définition précédente du mosaïque, cette dimension est supprimée de la forme en mosaïque et du vecteur de tuile. Par ailleurs, la limite du tableau de la dimension i-1 de la forme est augmentée de d_i-1 à d_id_i-1. Cette étape est répétée pour chaque astérisque dans le vecteur de tuiles.