Układ kafelkowy

Rysunek 1.

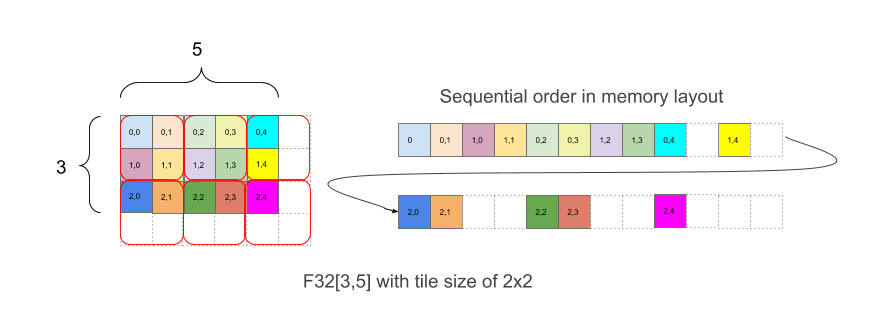
Rysunek 1 pokazuje układ tablicy F32[3,5] w pamięci z płytkami 2 x 2. Kształt z tym układem jest zapisywany jako F32[3,5]{1,0:T(2;2)}, gdzie 1,0 oznacza fizyczny porządek wymiarów (pole minor_to_major w układzie), a (2,2) po dwukropku oznacza kafelki wymiarów fizycznych kafelki o wymiarach 2 x 2.

Intuicyjnie układa się kafelki tak, aby zakrywały kształt, a następnie w poszczególnych kafelkach elementy są rozmieszczane bez ułożenia, tak jak w powyższym przykładzie, gdzie prawa część z przykładu pokazuje układ zapisany w pamięci, w tym białe elementy dopełniające, które zostały dodane w celu uzyskania pełnych kafelków 2 x 2, mimo że granice pierwotnej tablicy nie są równomierne.

Dodatkowe elementy w dopełnieniu nie muszą zawierać żadnej konkretnej wartości.

Wzory na indeks liniowy dla powtarzania kafelków o określonym kształcie i kafelku

Bez płytek element e=(e_n, e_n-1, ... , e₁) w tablicy o granicach tablicy d=(d_n, d_n-1, ... , d₁) (d1 to najbardziej mniejszy wymiar) jest układany w kolejności od największych do mniejszych:

linear_index(e, d)
= linear_index(((e_n, e_n-1; ... , e₁), (d_n, d_n-1, ... , d₁))
= e_nd_n-1...d₁ + e_n-1...d₁ + e_n-1 ...

Dla uproszczenia zapisu w tym dokumencie zakładamy, że kafelek ma taką samą liczbę wymiarów co tablica. W implementacji kafelków w XLA uogólnia się to na kafelki o mniejszych wymiarach, pozostawiając bez zmian początkowe najbardziej główne wymiary i stosowanie kafelków tylko do najmniejszych wymiarów. W ten sposób podany kafelek zawiera przyrostek wymiarów fizycznych ułożonego obok siebie kształtu.

Gdy używane jest ułożenie płytek o rozmiarze (t_n, t_n-1, ... , t₁), element tablicy z indeksami (e_n, e_n-1, ..., e₁) jest mapowany na tę pozycję w ostatecznym układzie:

_n, ⌈ ⌈ ⌈ ⌈ ⌈ ⌈ ⌈ ⌈ ⌈ ⌈ linear ⌋ ⌋e t ⌋ , e mod t , ( ⌈d/t⌉ t)


_n

Układ może składać się z 2 części: (⌊e_n/t_n⌋, ... , ⌊e₁/t₁⌋), co odpowiada indeksowi kafelków w tablicy o rozmiarach (⌈d_n/t_n⌉, ... , ≈d) Funkcja ceil pojawia się w ⌈d_i/t_i⌉, ponieważ jeśli kafelki przekraczają granice większej tablicy, dopełnienie jest wstawiane, jak na ilustracji 1. Kafelki i elementy wewnątrz kafelków są ułożone rekurencyjnie bez użycia płytek.

Na przykład na Rysunku 1 element (2,3) ma indeks kafelków (1,1) i indeks kafelka (0,1) dla połączonego wektora współrzędnych (1,1,0,1). Indeksy kafelków mają granice (2,3), a sam kafelek to (2,2) jako połączony wektor (2,3,2,2). Indeks liniowy z kafelkiem elementu o indeksie (2,3) w kształcie logicznym

linear_index_with_tile((2,3), (3,5), (2,2))
= indeks_liniowy((1,1,0,1), (2,3,2,2))
= indeks_liniowy((1,1), (2,3)) ∙ 2 ∙ 2 + indeks_liniowy(0,1) (2) + indeks_liniowy (0,1) (2,3,2,2)

Sąsiadująco z transpozycją zmiany kształtu

Układ oparty na fragmentach działa w ten sposób:
Rozważ zastosowanie tablicy wymiarów (d_n, d_n–1, ... , d1) (d1 to najmniejszy wymiar). Jeśli układa się z fragmentami o rozmiarze (t_n, t_n-1, ... , t₁) (najmniejszy wymiar to t₁), można je opisać za pomocą poniższego formatu.

1. Tablica jest dopełniana do (⌈d_n/t_n⌉∙t_n, ... , ⌈d₁/t₁⌉∙t₁).
2. Każdy wymiar i jest podzielony na (⌈d_i/ti⌉, t_i), tj. tablica zostaje zmieniona na
   (⌈d_n/t_n⌉, t_n, ... , ⌈d₁/t₁⌉, t₁).
   Ten sam model nie powoduje faktycznej zmiany układu, dlatego jest to sugestywny schemat. Jeśli nie myślisz o kafelkach, ta zmiana może wyrazić dowolny kształt z tą samą liczbą elementów co kształt z dopełnieniem. Tutaj widać, jak w ten sposób wyrazić kafelek.
3. Transponowanie polega na przeniesieniu t_n, ... , t₁ do najmniejszych wymiarów przy zachowaniu ich kolejności względnej, w ten sposób
   

Końcowy kształt ma prefiks
(⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉), który opisuje liczbę kafelków w każdym wymiarze. Element w tablicy (e_n, ... , e₁) jest mapowany na ten element w ostatecznym kształcie:
(⌊e_n/t_n⌋, ... , ⌊e₀/t₀⌋, e_n mod t_n, ... , e₁ mod). Wyraźnie widać, że indeks liniowy elementu odpowiada oczekiwanej zawartości zgodnie z tym wzorem.

Powtarzające się płytki

Płytki XLA staje się jeszcze bardziej elastyczne dzięki wielokrotnemu nakładaniu.

Rysunek 2.

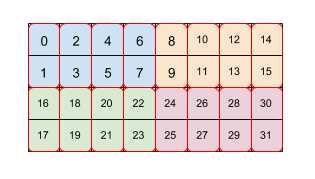
Rysunek 2 pokazuje, jak tablica o rozmiarze 4 x 8 jest ułożona na 2 poziomach płytek (najpierw 2 x 4, a następnie 2 x 1). Powtórzone kafelki oznaczamy jako (2,4)(2,1). Każdy kolor oznacza kafelek o wymiarach 2 x 4, a każde czerwone pole obramowania to kafelek 2 x 1. Liczby wskazują indeks liniowy w pamięci danego elementu w formacie kafelków. Ten format odpowiada formatowi stosowanemu w przypadku BF16 w TPU, z tym że początkowy kafelek jest większy, czyli jest to (8128)(2,1), gdzie drugi kafelek 2 x 1 ma na celu zebranie dwóch 16-bitowych wartości w celu utworzenia jednej 32-bitowej wartości w sposób zgodny z architekturą TPU.

Zwróć uwagę, że drugi lub późniejszy kafelek może odnosić się zarówno do mniejszych wymiarów kafelków, jak w tym przykładzie (8128)(2,1), ale może też odnosić się do głównych wymiarów kafelków z poprzednich kafelków.

Łączenie wymiarów za pomocą kafelków

Kafelki XLA obsługują też łączenie wymiarów. Funkcja ta może np. łączyć wymiary w komórce F32[2, 7,8,11,10]{4,3,2,1,0} z F32[112,110]{1,0}, a dopiero potem dodawać do niej komórki (2,3). Użyty kafelek to (∗,∗,2,∗,3). Gwiazdka w kafelku oznacza tu łączenie danego wymiaru z kolejnym, mniejszym wymiarem. Kilka sąsiadujących wymiarów można zebrać razem w jednym wymiarze. Podrzędny wymiar jest reprezentowany przez wartość kafelka równą -1 w danym wymiarze. Ten wymiar nie jest prawidłowy dla kafelka jako rozmiaru.

Mówiąc dokładniej, jeśli wymiar i kształtu zostanie usunięty za pomocą gwiazdki w kafelku, to zanim zostanie zastosowana poprzednia definicja płytek, wymiar ten zostanie usunięty zarówno z kształtu, jak i wektora kafelka, a wymiar i-1 kształtu zostanie zwiększony z d_i-1 do d_id_i-1. Ten krok powtarza się dla każdej gwiazdki we wektorze kafelka.