Layout em mosaico

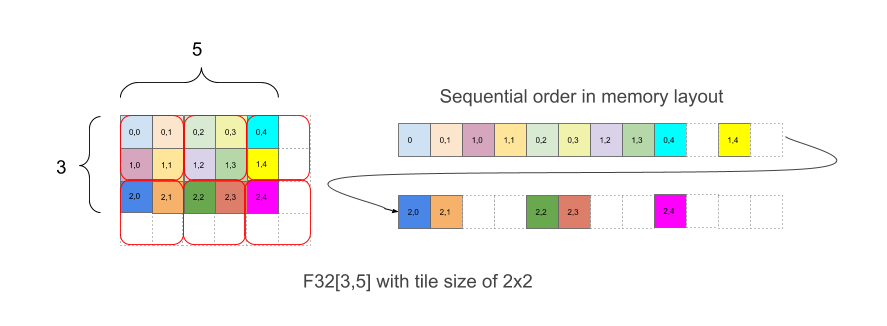
Figura 1

A Figura 1 mostra como uma matriz F32[3,5] é disposta na memória com blocos 2x2. Uma forma com esse layout é escrita como F32[3,5]{1,0:T(2,2)}, em que 1,0 se refere à ordem física das dimensões (campo minor_to_major no Layout), enquanto (2,2) após os dois-pontos indica o agrupamento das dimensões físicas por um bloco 2x2.

Intuitivamente, os blocos são dispostos para cobrir a forma e, dentro de cada bloco, os elementos são dispostos sem blocos, como no exemplo acima, em que a parte direita mostra o layout na memória, incluindo os elementos de padding brancos que são adicionados para ter blocos de 2 x 2 completos, mesmo que os limites originais da matriz não sejam uniformes.

Os elementos extras no padding não precisam conter nenhum valor específico.

Fórmulas de índice linear para agrupamento com base em uma forma e um bloco

Sem agrupamento, um elemento e=(e_n, e_n-1, ... , e₁) em uma matriz com limites de matriz d=(d_n, d_n-1, ... , d₁) (d1 é a dimensão mais secundária) é disposto de maior para ordem secundária na posição:

linear_index(e, d)
= linear_index((e_n, e_n-1, ... , e₁), (d_n, d_n-1, ... , d₁))
= e_nd_n-1...d₁ + e_n-1d_n-2

Para simplificar a notação neste documento, presumimos que um bloco tem o mesmo número de dimensões que a matriz. Na implementação do agrupamento do XLA, isso é generalizado para blocos com menos dimensões, deixando as dimensões mais principais iniciais inalteradas e aplicando-os somente às dimensões mais secundárias, de modo que o agrupamento especificado mencione um sufixo das dimensões físicas da forma que está sendo dividida.

Quando o bloco de tamanho (t_n, t_n-1, ... , t₁) é usado, um elemento na matriz com índices (e_n, e_n-1, ... , e₁) é mapeado para esta posição no layout final:

_nnnt/t_{nnnnnnnnnnnnnnnnnn}

O layout pode ser pensado como tendo duas partes: (⌊e_n/t_n⌋, ... , ⌊e₁/t₁⌋), que corresponde a um índice de blocos em uma matriz de blocos de tamanho (⌈d_n/t_n⌉, ⌉1, mod₁/teta, ⌉1₁/correspondente, _{A função ceil aparece em ⌈di/ti⌉ porque, se os blocos ultrapassarem os limites da matriz maior, o preenchimento será inserido como na Figura 1. Os blocos e os elementos dentro de blocos são dispostos de maneira recursiva, sem blocos.}

No exemplo da Figura 1, o elemento (2,3) tem um índice de blocos (1,1) e um índice dentro de blocos (0,1), para um vetor de coordenadas combinado de (1,1,0,1). Os índices de blocos têm limites (2,3) e o próprio bloco é (2,2) para um vetor combinado de (2,3,2,2). O índice linear com bloco para o elemento com índice (2,3) na forma lógica é então

Ladrilho como pad-reshape-transpose

O layout baseado em blocos funciona da seguinte maneira:
Considere uma matriz de dimensões (d_n, d_n-1, ... , d1) (d1 é a dimensão mais secundária). Quando ele está disposto com blocos de tamanho (t_n, t_n-1, ... , t₁) (t₁ é a dimensão mais menor), esse agrupamento pode ser descrito em termos de pad-reshape-transpose da seguinte maneira.

1. A matriz é preenchida com (⌈d_n/t_n⌉∙t_n, ... , ⌈d₁/t₁⌉∙t₁).
2. Cada dimensão i é dividida em (⌈d_i/ti⌉, t_i), ou seja, a matriz é remodelada para
   (⌈d_n/t_n⌉, t_n, ... , ⌈d₁/t₁⌉, t₁).
   Não há mudança física de layout nessa remodelação por si só, então ela é um bitcast. Se não estiver pensando explicitamente em um bloco, essa reforma poderá expressar qualquer forma com o mesmo número de elementos que a forma preenchida. Este exemplo mostra como expressar um bloco dessa maneira.
3. A transposição acontece ao mover t_n, ... , t₁ para as dimensões mais secundárias, mantendo sua ordem relativa, de modo que a ordem das dimensões do maior para o menor se torna
   (⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉, t_n, t_n).

A forma final tem o prefixo
(⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉), que descreve o número de blocos em cada dimensão. Um elemento na matriz (e_n, ... , e₁) é mapeado para esse elemento na forma final:
(⌊e_n/t_n⌋, ... , ⌊e₀/t₀⌋, e_n mod t_n, ... , e₁ mod). É fácil ver que o índice linear do elemento segue a fórmula acima, conforme esperado.

Blocos repetidos

O agrupamento do XLA se torna ainda mais flexível ao aplicá-lo repetidamente.

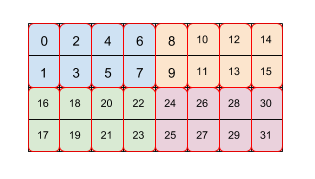
Figura 2

A Figura 2 mostra como uma matriz de tamanho 4x8 é dividida em dois níveis de blocos (primeiro 2x4, depois 2x1). Representamos esse agrupamento repetido como (2,4)(2,1). Cada cor indica um bloco de 2 x 4 e cada caixa de borda vermelha é um bloco de 2 x 1. Os números indicam o índice linear na memória desse elemento no formato lado a lado. Esse formato corresponde ao usado para BF16 na TPU, exceto pelo fato do bloco inicial ser maior, ou seja, o agrupamento é (8.128)(2,1). O objetivo do segundo bloco por 2x1 é coletar dois valores de 16 bits para formar um valor de 32 bits de forma alinhada com a arquitetura de uma TPU.

Um segundo ou mais tarde pode se referir às duas dimensões menores dentro do bloco, o que apenas reorganiza os dados dentro do bloco, como neste exemplo com (8,128)(2,1), mas também pode se referir às principais dimensões de bloco cruzado do bloco anterior.

Combinar dimensões usando blocos

O agrupamento do XLA também é compatível com a combinação de dimensões. Por exemplo, ele pode combinar dimensões em F32[2,7,8,11,10]{4,3,2,1,0} em F32[112,110]{1,0} antes de agrupar com (2,3). O bloco usado é (∗,∗,2,*,3). Aqui, um asterisco em um bloco implica usar essa dimensão e combiná-la com a próxima dimensão mais secundária. Várias dimensões adjacentes podem ser agrupadas em uma dimensão. Uma dimensão incluída é representada por um valor de bloco de -1 nessa dimensão do bloco, que não é válida em um bloco como um tamanho de dimensão.

Mais precisamente, se a dimensão i da forma for eliminada por um asterisco no bloco, antes da aplicação da definição anterior de bloco, essa dimensão será removida da forma que está sendo ladrilhada e do vetor de bloco. E a dimensão i-1 da forma terá o limite de matriz aumentado de d_i-1 para d_id_i-1. Essa etapa é repetida para cada asterisco no vetor de bloco.