Рисунок 1
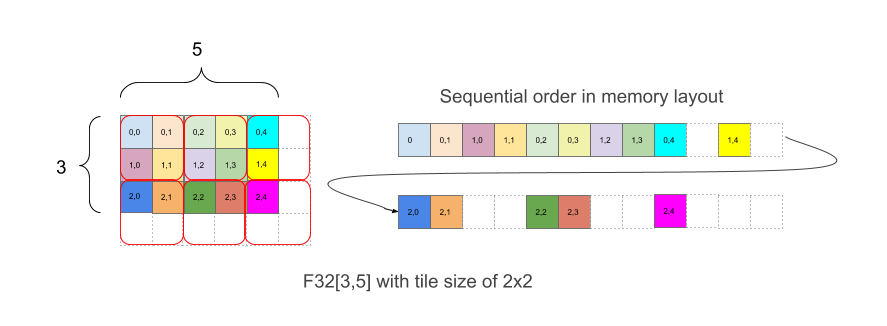
На рисунке 1 показано, как массив F32[3,5] размещается в памяти с тайлингом 2x2. Фигура с таким макетом записывается как F32[3,5]{1,0:T(2,2)}, где 1,0 относится к физическому порядку размеров (поле minor_to_major в макете), а (2,2) после двоеточия указывает на мозаику физических измерений плиткой 2x2.
Интуитивно понятно, что плитки раскладываются так, чтобы покрыть форму, а затем внутри каждой плитки элементы располагаются без мозаики, как в примере выше, где правая часть примера показывает макет в памяти, включая белые элементы заполнения, которые добавлен для того, чтобы иметь полные плитки 2x2, даже если исходные границы массива нечетные.
Дополнительные элементы в отступе не обязаны содержать какое-либо конкретное значение.
Формулы линейного индекса для укладки плитки с учетом формы и плитки
Без мозаики элемент e=( en , e n-1 , ... , e 1 ) в массиве с границами массива d=(d n , d n-1 , ... , d 1 ) (d1 самое младшее измерение) располагается в порядке возрастания к младшему в позиции:
линейный_индекс (е, г)
= линейный_индекс((en , e n-1 , ... , e 1 ), (d n , d n-1 , ... , d 1 ))
= е н д н-1 ...д 1 + е н-1 д н-2 ...д 1 + ... + е 1
Для простоты обозначений в этом документе мы предполагаем, что плитка имеет то же количество измерений, что и массив. В реализации мозаики XLA это обобщается на мозаику с меньшим количеством измерений, оставляя первоначальные самые главные измерения неизменными и применяя мозаику только к самым младшим измерениям, так что указанная мозаика упоминает суффикс физических размеров форма, выложенная плиткой.
При использовании тайла размера (t n , t n-1 , ... , t 1 ) элемент массива с индексами (en , en -1 , ... , e 1 ) сопоставляется с этим позиция в окончательном макете:
линейный_индекс_с_плитой (е, d, т)
= линейный_индекс((⌊e/t⌋, e mod t), (⌈d/t⌉, t)) (арифметика поэлементная, (a,b) — конкатенация)
= линейный_индекс((⌊e n /t n ⌋, ... , ⌊e 1 /t 1 ⌋, e n mod t n , ... , e 1 mod t 1 ), (⌈d n /t n ⌉, ... , ⌈d 1 /t 1 ⌉, t n , t n-1 , ... , t 1 ))
= линейный_индекс((⌊e n /t n ⌋, ... , ⌊e 1 /t 1 ⌋), (⌈d n /t n ⌉, ... , ⌈d 1 /t 1 ⌉))∙t n t n-1 ...t 1 + linear_index(( en mod t n , ... , e 1 mod t 1 ), (t n , t n-1 , ... , t 1 ))
Макет можно рассматривать как состоящий из двух частей: (⌊e n /t n ⌋, ..., ⌊e 1 /t 1 ⌋), что соответствует индексу тайла в массиве тайлов размера (⌈d n /t n ⌉, ... , ⌈d 1 /t 1 ⌉) и (e n mod t n , ... , e 1 mod t 1 ), что соответствует индексу внутри плитки. Функция ceil появляется в ⌈d i /t i ⌉, потому что, если плитки выходят за границы большего массива, вставляется заполнение, как показано на рисунке 1. И плитки, и элементы внутри плиток размещаются рекурсивно без мозаики.
В примере на рисунке 1 элемент (2,3) имеет индекс фрагмента (1,1) и индекс внутри фрагмента (0,1) для комбинированного координатного вектора (1,1,0,1). Индексы плитки имеют границы (2,3), а сама плитка равна (2,2) для комбинированного вектора (2,3,2,2). Тогда линейный индекс с плиткой для элемента с индексом (2,3) в логической форме равен
линейный_индекс_с_плитой((2,3), (3,5), (2,2))
= линейный_индекс((1,1,0,1), (2,3,2,2))
= линейный_индекс((1,1), (2,3)) ∙ 2 ∙ 2 + линейный_индекс((0,1), (2,2))
= (1 ∙ 3 + 1) ∙ 2 ∙ 2 + (0 ∙ 2 + 1)
= 17.
Мозаика в виде Pad-Reshape-Transpose
Компоновка на основе тайлов работает следующим образом:
Рассмотрим массив измерений (d n , d n-1 , ..., d1) (d1 — самое младшее измерение). Когда он выложен мозаикой размера (t n , t n-1 , ... , t 1 ) (t 1 — самое незначительное измерение), эту мозаику можно описать в терминах Pad-Reshape-Transpose следующим образом: способ.
- Массив дополняется до (⌈d n /t n ⌉∙t n , ... , ⌈d 1 /t 1 ⌉∙t 1 ).
- Каждое измерение i разбивается на (⌈d i /t i ⌉, t i ), т. е. массив преобразуется в
(⌈d n /t n ⌉, t n , ... , ⌈d 1 /t 1 ⌉, t 1 ).
Само по себе это изменение формы не приводит к изменению физического макета, поэтому это изменение является битовым. Если не думать о мозаике явно, то это изменение формы может выражать любую фигуру с тем же количеством элементов, что и фигура с заполнением — здесь приведен пример того, как выразить плитку таким способом. - Транспонирование происходит путем перемещения t n , ... , t 1 к самым младшим измерениям, сохраняя при этом их относительный порядок, так что порядок измерений от самого главного к самому младшему становится
(⌈d n /t n ⌉, ... , ⌈d 1 /t 1 ⌉, t n , ... , t 1 ).
Окончательная форма имеет префикс
(⌈d n /t n ⌉, ..., ⌈d 1 /t 1 ⌉), который описывает количество плиток в каждом измерении. Элемент массива ( en , ..., e 1 ) сопоставляется с этим элементом в окончательной форме:
(⌊e n /t n ⌋, ..., ⌊e 0 /t 0 ⌋, e n mod t n , ... , e 1 mod t 1 ). Легко видеть, что линейный индекс элемента соответствует приведенной выше формуле, как и ожидалось.
Повторяющаяся мозаика
Мозаика XLA становится еще более гибкой за счет многократного применения.
фигура 2
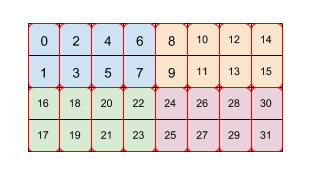
На рис. 2 показано, как массив размером 4x8 разбивается на два уровня (сначала 2x4, затем 2x1). Мы представляем это повторяющееся замощение как (2,4)(2,1). Каждый цвет обозначает плитку 2х4, а каждая красная рамка — плитку 2х1. Числа указывают линейный индекс в памяти этого элемента в мозаичном формате. Этот формат соответствует формату, используемому для BF16 на TPU, за исключением того, что начальный тайл больше, а именно, тайл (8,128)(2,1), где цель второго тайла 2x1 состоит в том, чтобы собрать вместе два 16-битных значения. для формирования одного 32-битного значения таким образом, чтобы оно соответствовало архитектуре TPU.
Обратите внимание, что вторая или более поздняя плитка может относиться как к второстепенным измерениям внутри плитки, которые просто переупорядочивают данные внутри плитки, как в этом примере с (8,128)(2,1), но также может относиться к основному межплиточному размеру. размеры предыдущей плитки.
Объединение размеров с помощью тайлов
Мозаика XLA также поддерживает объединение размеров. Например, он может сначала объединить размеры из F32[2,7,8,11,10]{4,3,2,1,0} в F32[112,110]{1,0}, прежде чем объединять их с помощью (2,3 ). Используется плитка (∗,∗,2,∗,3). Здесь звездочка на плитке означает взятие этого измерения и объединение его со следующим, более мелким измерением. Несколько смежных измерений могут быть объединены в одно измерение. Включенное измерение представлено значением плитки -1 в этом измерении плитки, которое в противном случае недействительно для плитки в качестве размера измерения.
Точнее, если измерение i формы исключается с помощью звездочки в плитке, то перед применением предыдущего определения мозаики это измерение удаляется как из фигуры, которая замощается мозаикой, так и из вектора плитки, а также из того, что было размером i-1. Граница массива фигуры увеличена с d i-1 до di d i-1 . Этот шаг повторяется для каждой звездочки в векторе мозаики.

