เลย์เอาต์แบบเรียงชิดกัน

รูปที่ 1

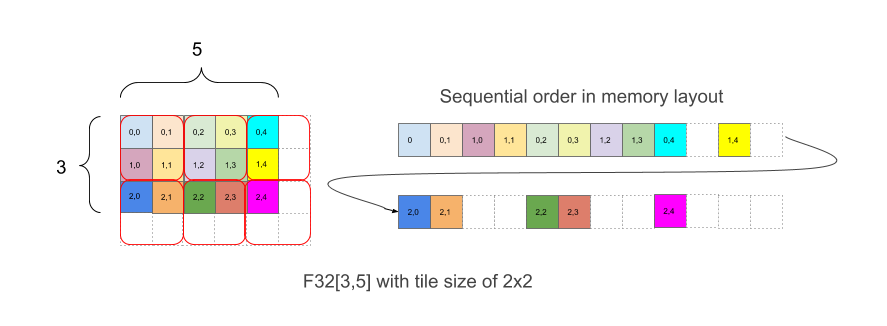
รูปที่ 1 แสดงวิธีวางอาร์เรย์ F32[3,5] ในหน่วยความจำที่ต่อด้วยกระเบื้องขนาด 2x2 รูปร่างของเลย์เอาต์นี้จะเขียนเป็น F32[3,5]{1,0:T(2,2)} โดยที่ 1,0 เกี่ยวข้องกับลำดับทางกายภาพของขนาด (ช่อง minor_to_major ในเลย์เอาต์) ขณะที่ (2,2) หลังเครื่องหมายโคลอนหมายถึงการเรียงต่อกันของขนาดทางกายภาพด้วยไทล์ขนาด 2x2

ในความเป็นจริง ระบบจะวางชิ้นส่วนเพื่อให้ครอบคลุมรูปร่าง จากนั้นภายในแต่ละชิ้นส่วน องค์ประกอบจะวางโดยไม่มีการเรียงต่อกันอย่างในตัวอย่างด้านบน โดยส่วนด้านขวาของตัวอย่างแสดงเลย์เอาต์ในหน่วยความจำ ซึ่งรวมถึงองค์ประกอบ Padding สีขาวที่เพิ่มเข้ามาเพื่อให้มีชิ้นส่วนขนาด 2x2 ที่สมบูรณ์ แม้ว่าขอบเขตของอาร์เรย์เดิมจะไม่เท่ากันก็ตาม

องค์ประกอบเพิ่มเติมในระยะห่างจากขอบไม่จำเป็นต้องมีค่าใดๆ โดยเฉพาะ

สูตรดัชนีเชิงเส้นสำหรับการเรียงต่อชิ้นส่วนตามรูปร่างและชิ้นส่วน

หากไม่มีการเรียงต่อกัน องค์ประกอบ e=(e_n, e_n-1, ... , e₁) ในอาร์เรย์ที่มีขอบเขตอาร์เรย์ d=(d_n, d_n-1, ... , d₁) (d1 คือมิติข้อมูลรองมากที่สุด) จะมีการจัดวางตามลําดับหลักจนถึงลำดับรองที่ตำแหน่ง

linear_index(e, d)
= linear_index((e_n, e_n-1, ... , e₁), (d_n, d_n-1, ... , d₁))
= e_nd_n-1...d₁ + _n + 1

เพื่อให้อธิบายได้ง่ายขึ้นในเอกสารนี้ เราถือว่าไทล์มีจำนวนมิติข้อมูลเท่ากับอาร์เรย์ ในการใช้งานการเรียงไทล์ของ XLA โดยทั่วไปแล้วจะหมายถึงการเรียงขนาดที่มีขนาดน้อยกว่าโดยคงขนาดหลักแรกไว้เหมือนเดิม และใช้การเรียงต่อกับขนาดเล็กๆ เท่านั้น เพื่อให้ไทล์ที่ระบุกล่าวถึงส่วนต่อท้ายของขนาดจริงของรูปร่างที่ถูกเรียงต่อกัน

เมื่อใช้การเรียงต่อขนาด (t_n, t_n-1, ... , t₁) องค์ประกอบในอาร์เรย์ที่มีดัชนี (e_n, e_n-1, ... , e₁) จะจับคู่กับตำแหน่งนี้ในเลย์เอาต์สุดท้าย

<a x_n,_nnn

ซึ่งเลย์เอาต์จะมี 2 ส่วนดังต่อไปนี้ (⌊e_n/t_n⌋, ... , ⌊e₁/t₁⌋) ซึ่งสอดคล้องกับดัชนีไทล์ในอาร์เรย์ของชิ้นส่วนขนาด (⌈d_n/t_n⌉, ..._cors,₁ ฟังก์ชัน Ceil จะปรากฏใน ⌈d_i/t_i⌉ เนื่องจากหากไทล์เกินขอบเขตของอาร์เรย์ที่ใหญ่กว่า ระบบจะแทรกระยะห่างจากขอบดังรูปที่ 1 ทั้งชิ้นส่วนและองค์ประกอบภายในชิ้นส่วนจะจัดวางซ้ำโดยไม่มีการเรียงต่อกัน

สำหรับตัวอย่างในรูปที่ 1 องค์ประกอบ (2,3) มีดัชนีไทล์ (1,1) และดัชนีภายในไทล์ (0,1) เป็นเวกเตอร์พิกัดร่วมของ (1,1,0,1) ดัชนีไทล์มีขอบเขต (2,3) และตัวไทล์เองคือ (2,2) สำหรับเวกเตอร์รวมของ (2,3,2,2) จากนั้นดัชนีเชิงเส้นที่มีไทล์สำหรับองค์ประกอบที่มีดัชนี (2,3) ในรูปร่างเชิงตรรกะ

linear_index_with_tile((2,3), (3,5), (2,2))
= linear_index((1,1,0,1), (2,3,2,2))
= linear_index((1,1), (2,3)) ∙ ∙ 2 ∙ 2, 2))
= linear_index((1,1,0,1), (2,3,2,2))
= linear_index((1,1), (2,3)) ∙ 2 ∙ 2 + ∙ x ∙(0,1) (2,2)

การเรียงสับเปลี่ยนรูปร่างแพดเดิลโพรเซส

เลย์เอาต์แบบเรียงต่อกันมีลักษณะการทำงานดังนี้
พิจารณาอาร์เรย์ของมิติข้อมูล (d_n, d_n-1, ... , d1) (d1 เป็นมิติข้อมูลที่เล็กที่สุด) เมื่อวางชิ้นส่วนขนาด (t_n, t_n-1, ... , t₁) (t₁ คือขนาดย่อยที่สุด) การเรียงชิ้นส่วนดังกล่าวสามารถอธิบายในรูปแบบการเปลี่ยนรูปร่างแพดได้ดังต่อไปนี้

1. อาร์เรย์จะเสริมตาม (⌈d_n/t_n⌉∙t_n, ... , ⌈d₁/t₁⌉∙t₁)
2. มิติข้อมูลแต่ละรายการ i แบ่งออกเป็น (⌈d_i/ti⌉, t_i) กล่าวคือ อาร์เรย์จะเปลี่ยนรูปร่างเป็น
   (⌈d_n/t_n⌉, t_n, ... , ⌈d₁/t₁⌉, t₁)
   ไม่มีการเปลี่ยนแปลงเลย์เอาต์ทางกายภาพในการปรับรูปร่างนี้ การปรับเปลี่ยนรูปร่างนี้จึงเป็นเหมือนบิตแคสต์ หากไม่มีการคิดแบบเรียงต่อกันอย่างชัดเจน การปรับรูปร่างนี้สามารถแสดงรูปร่างใดก็ได้ที่มีจำนวนองค์ประกอบเท่ากับรูปร่างที่เพิ่ม ตัวอย่างต่อไปนี้คือวิธีการแสดงชิ้นส่วนในลักษณะนี้
3. การสลับเปลี่ยนจะเกิดขึ้นโดยเลื่อน _n, ... , t₁ ไปยังมิติข้อมูลรองที่มากที่สุดขณะคงลำดับแบบสัมพัทธ์ เพื่อให้ลำดับของมิติข้อมูลจากส่วนใหญ่ไปส่วนใหญ่เป็น
   (⌈d_n/t_n⌉, ... , ⌈d₁/t₁, _n)

รูปร่างสุดท้ายจะมีคำนำหน้า
(⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉) ซึ่งอธิบายจำนวนชิ้นส่วนในแต่ละมิติข้อมูล องค์ประกอบในอาร์เรย์ (e_n, ... , e₁) จะแมปกับองค์ประกอบนี้ในรูปร่างสุดท้าย ดังนี้
(⌊e_n/t_n⌋, ... , ⌊e₀/t₀⌋, e_n mod t_n, ... , e₁) สังเกตได้ง่ายๆ ว่าดัชนีเชิงเส้นขององค์ประกอบ เป็นไปตามสูตรด้านบนตามที่คาดไว้

การปูกระเบื้องซ้ำ

การเรียงไทล์ของ XLA ยิ่งยืดหยุ่นมากขึ้นโดยการนำมาปรับใช้ซ้ำๆ

รูปที่ 2

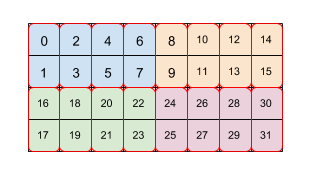
รูปที่ 2 แสดงวิธีจัดเรียงอาร์เรย์ขนาด 4x8 โดยการเรียงต่อกัน 2 ระดับ (2x4 แรกและ 2x1) เราแสดงการเรียงซ้ำแบบซ้ำกันนี้เป็น (2,4)(2,1) แต่ละสีหมายถึงช่องขนาด 2x4 และกล่องเส้นขอบสีแดงแต่ละกล่องคือชิ้นส่วนขนาด 2x1 ตัวเลขจะระบุดัชนีเชิงเส้นในหน่วยความจำขององค์ประกอบดังกล่าวในรูปแบบเรียงต่อกัน รูปแบบนี้ตรงกับรูปแบบที่ใช้สำหรับ BF16 บน TPU เว้นแต่ว่าไทล์เริ่มต้นจะมีขนาดใหญ่ขึ้น กล่าวคือ ไทล์คือ (8,128)(2,1) ซึ่งวัตถุประสงค์ของไทล์ที่ 2 ขนาด 2x1 คือการรวบรวมค่า 16 บิต 2 ค่าเข้าด้วยกันเพื่อสร้างค่า 32 บิต 1 ค่าโดยสอดคล้องกับสถาปัตยกรรมของ TPU

โปรดทราบว่าไทล์ที่ 2 ขึ้นไปอาจหมายถึงทั้งมิติข้อมูลภายในชิ้นส่วนย่อยทั้งคู่ ซึ่งแค่จัดเรียงข้อมูลใหม่ภายในชิ้นส่วนดังกล่าว ตามที่แสดงในตัวอย่างนี้ด้วย (8,128)(2,1) แต่อาจหมายถึงมิติข้อมูลครอสไทล์หลักจากชิ้นส่วนก่อนหน้า

การรวมมิติข้อมูลโดยใช้ชิ้นส่วน

การเรียงไทล์ของ XLA ยังรองรับมิติข้อมูลแบบผสมด้วย เช่น สามารถรวมมิติข้อมูลใน F32[2,7,8,11,10]{4,3,2,1,0} เป็น F32[112,110]{1,0} ก่อนที่จะเรียงต่อกับ (2,3) ชิ้นส่วนที่ใช้คือ (红,ล็อก,2,คุณ,3) นี่คือเครื่องหมายดอกจันในไทล์ที่หมายถึงการนำมิติข้อมูลนั้นไปรวมกับมิติข้อมูลรองที่ใหญ่กว่า มิติข้อมูลที่อยู่ติดกันหลายรายการสามารถรวมอยู่ใน มิติข้อมูลเดียวได้ มิติข้อมูลย่อยจะแสดงด้วยค่าไทล์ที่ -1 ในมิติข้อมูลของไทล์นั้น ซึ่งไม่มีในไทล์ที่เป็นขนาดมิติข้อมูล

กล่าวคือ หากมิติ i ของรูปร่างถูกตัดออกผ่านเครื่องหมายดอกจันในไทล์ ก่อนที่จะมีการใช้การกำหนดไทล์ก่อนหน้านี้ มิติข้อมูลนั้นจะถูกลบออกจากทั้งรูปร่างที่แยกชิ้นส่วนและเวกเตอร์ของชิ้นส่วน และมิติข้อมูล i-1 ของรูปร่างมีขอบเขตอาร์เรย์เพิ่มขึ้นจาก d_i-1 เป็น d_id_i-1 ขั้นตอนนี้จะเล่นซ้ำสำหรับเครื่องหมายดอกจันแต่ละตัวในเวกเตอร์ของไทล์