Abbildung 1
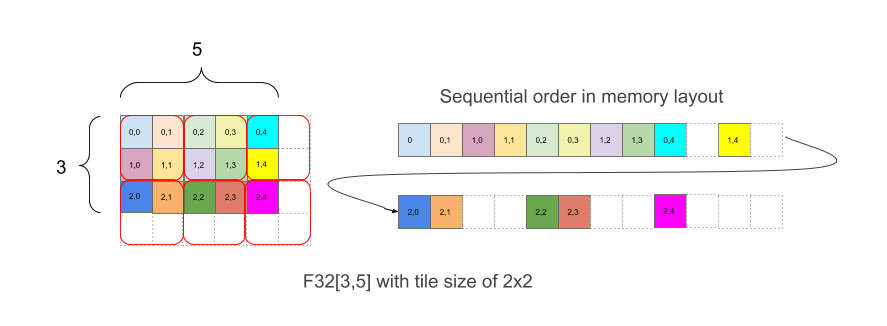
Abbildung 1 zeigt, wie ein Array F32[3,5] im Speicher mit 2x2-Kacheln angeordnet ist. Eine Form mit diesem Layout wird als F32[3,5]{1,0:T(2;2)} geschrieben,wobei sich 1,0 auf die physische Reihenfolge der Dimensionen (Feld minor_to_major im Layout) bezieht,während (2,2) nach dem Doppelpunkt die Kachel der physischen Abmessungen durch eine 2x2-Kachel darstellt.
Intuitiv werden Kacheln so angeordnet, dass sie die Form abdecken. Dann werden innerhalb jeder Kachel Elemente ohne Kacheln angeordnet, wie im obigen Beispiel, wobei der rechte Teil des Beispiels das Layout im Speicher zeigt, einschließlich der weißen Padding-Elemente, die hinzugefügt werden, um vollständige 2x2-Kacheln zu erhalten, obwohl die ursprünglichen Arraygrenzen nicht gleichmäßig sind.
Die zusätzlichen Elemente im Abstand müssen keinen bestimmten Wert enthalten.
Lineare Indexformeln für Kacheln mit einer Form und einer Kachel
Ohne Tile-Funktion wird ein Element e=(en, en-1, ... , e1) in einem Array mit den Arraygrenzen d=(dn, dn-1, ... , d1) (d1 ist die kleinste Dimension) von der Haupt- bis zur Nebenordnung an der Position angeordnet:
linear_index(e, d)
= linear_index((en, en-1, ... , e1),
(dn, dn-1, ... , d1))
= endn-1...d1 +
en-1 + en-1...
Zur Vereinfachung der Notation in diesem Dokument gehen wir davon aus, dass eine Kachel die gleiche Anzahl von Dimensionen wie das Array hat. In der XLA-Implementierung von Tiling wird dies auf Tilings mit weniger Abmessungen verallgemeinert, indem die ersten größeren Abmessungen unverändert bleiben und die Tile-Funktion nur auf die kleinsten Dimensionen angewendet wird, sodass die angegebene Tile ein Suffix der physischen Abmessungen der gekachelten Form enthält.
Bei der Verwendung von Kacheln der Größe (tn, tn-1, ... , t1) wird ein Element im Array mit Indexen (en, en-1, ... , e1) dieser Position im endgültigen Layout zugeordnet:
n
Das Layout besteht aus zwei Teilen: (⌊en/tn⌋, ... , ⌊e1/t1⌋), die einem Kachelindex in einem Array von Kacheln der Größe (⌈dn/tn⌉, ... , cn⌉, ... , ⌋⌉, ... , ⌋ ⌉, ... , ⌋ ⌉(1 - 1) entspricht1/⌈), und 1(1 - 1) entspricht1/t11 Die Ceil-Funktion wird in ⌈di/ti⌉ angezeigt, denn wenn Kacheln die Grenzen des größeren Arrays überschreiten, wird das Padding wie in Abbildung 1 eingefügt. Sowohl die Kacheln als auch die darin enthaltenen Elemente werden rekursiv ohne Kacheln angeordnet.
Im Beispiel in Abbildung 1 hat das Element (2,3) einen Kachelindex (1,1) und einen Index innerhalb des Kacheln (0,1) für einen kombinierten Koordinatenvektor von (1,1,0,1). Die Kachelindexe haben Grenzen (2,3) und die Kachel selbst ist (2,2) für einen kombinierten Vektor von (2,3,2,2). Der lineare Index mit der Kachel für das Element mit dem Index (2,3) in der logischen Form ist dann
linear_index_with_tile((2,3), (3,5), (2,2))
= linear_index((1,1,0,1), (2,3,2,2))
= linear_index((1,1), (2,3)) ∙ 2 ∙ 2 + linear_index((0,1) ∙ 2 + linear_index((0,1)) ∙ 2 + 1)
Tiling als pad-reshape-transpose
Das kachelbasierte Layout funktioniert so:
Betrachten Sie ein Array von Dimensionen (dn, dn-1, ... , d1) (d1 ist die kleinste Dimension). Wenn sie mit Kacheln der Größe (tn, tn-1, ... , t1) ausgelegt wird (t1 ist die kleinste Dimension), lässt sich diese Kachel in Form von "pad-reshape-transpose" beschreiben.
- Das Array wird aufgefüllt auf (⌈dn/tn⌉∙tn, ... , ⌈d1/t1⌉∙t1).
- Jede Dimension i wird in (⌈di/ti⌉, ti) unterteilt, d.h. das Array wird zu
(⌈dn/tn⌉, tn, ... , ⌈d1/t1⌉, t1) umgeformt.
Bei dieser Umformung selbst gibt es keine physische Layoutänderung. Diese Umformung ist also eine Bitcast-Transformation. Wenn Sie nicht explizit an eine Kachel denken, könnte diese Umformung jede Form ausdrücken, die dieselbe Anzahl von Elementen wie die aufgefüllte Form hat. Im folgenden Beispiel sehen Sie, wie eine Kachel auf diese Weise ausgedrückt wird. - Beim Transponieren wird tn, ... , t1 zu den kleinsten Dimensionen verschoben, dabei aber ihre relative Reihenfolge beibehalten, sodass die Reihenfolge der Dimensionen vom größten zum kleinsten Teil zu
(⌈dn/tn⌉, ... , ⌈d1/t1⌉, tn wird.
Die letzte Form hat das Präfix
(⌈dn/tn⌉, ... ,
⌈d1/t1⌉), das die Anzahl der Kacheln in jeder Dimension beschreibt. Ein Element im Array (en, ... , e1) wird diesem Element in der endgültigen Form zugeordnet:
(⌊en/tn⌋, ... ,
⌊e0/t0⌋, en mod tn, ... , e1). Es ist leicht zu erkennen, dass der lineare Index des Elements wie erwartet der obigen Formel folgt.
Wiederholtes Tiling
Das Tiling von XLA wird noch flexibler, da es wiederholt angewendet wird.
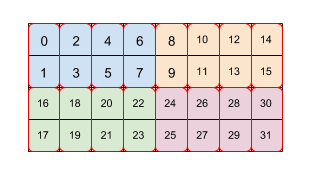
Abbildung 2
Abbildung 2 zeigt, wie ein Array der Größe 4 x 8 durch zwei Kacheln gekachelt wird (zuerst 2 x 4, dann 2 x 1). Diese wiederholte Tile-Funktion wird als (2;4)(2;1) dargestellt. Jede Farbe steht für eine 2x4-Kachel und jedes rote Rahmenfeld ist eine 2x1-Kachel. Die Zahlen geben den linearen Index dieses Elements im Kachelformat an. Dieses Format entspricht dem Format, das für BF16 auf TPU verwendet wird, mit der Ausnahme, dass die anfängliche Kachel größer ist, nämlich (8,128)(2,1), wobei der Zweck der zweiten Kachel mit 2x1 darin besteht, zwei 16-Bit-Werte zu einem 32-Bit-Wert zusammenzuführen, der der Architektur einer TPU entspricht.
Beachten Sie, dass sich eine zweite oder eine spätere Kachel auf beide Nebenabmessungen innerhalb der Kachel beziehen kann. Dadurch werden nur die Daten innerhalb der Kachel neu angeordnet, wie in diesem Beispiel mit (8,128)(2,1), aber auch auf die Hauptdimensionen innerhalb der Kachel.
Dimensionen mithilfe von Kacheln kombinieren
Die Tile-Funktion von XLA unterstützt auch die Kombination von Dimensionen. Beispielsweise können die Dimensionen in F32[2, 7,8,11,10]{4,3,2,1,0} zuerst in F32[112,110]{1,0} kombiniert werden,bevor sie mit (2,3) gekachelt wird. Die verwendete Kachel ist (∗,∗,2,∗,3). Hier bedeutet ein Sternchen in einer Kachel, dass diese Dimension mit der nächstgrößeren kleineren Dimension kombiniert wird. Mehrere benachbarte Dimensionen können zusammen zu einer Dimension zusammengefasst werden. Eine subsumierte Dimension wird durch einen Kachelwert von -1 in dieser Dimension der Kachel dargestellt, der ansonsten in einer Kachel als Dimensionsgröße nicht gültig ist.
Genauer gesagt: Wenn die Dimension i der Form durch ein Sternchen in der Kachel entfernt wird, wird diese Dimension vor Anwendung der vorherigen Definition von Kacheln sowohl aus der gekachelten Form als auch vom Kachelvektor entfernt. Bei der Dimension i-1 der Form wird ihre Arraygrenze von di-1 auf didi-1 erhöht. Dieser Schritt wird für jedes Sternchen im Kachelvektor wiederholt.

