Karo düzeni

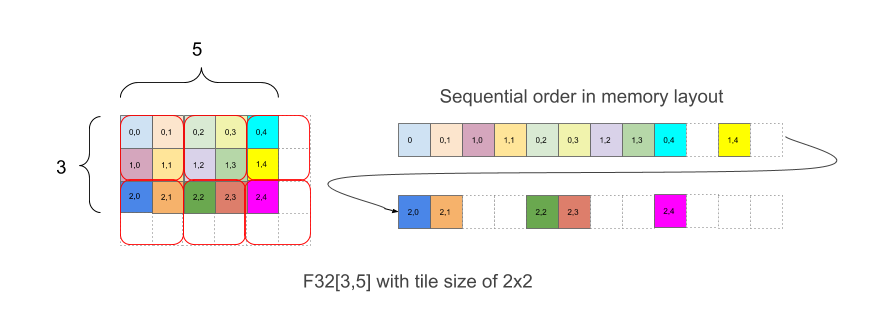
Şekil 1

Şekil 1'de, bir F32[3,5] dizisinin 2x2 karolarla nasıl belleğe yerleştirildiği gösterilmektedir. Bu düzene sahip bir şekil F32[3,5]{1,0:T(2,2)} şeklinde yazılır. Burada, 1,0 boyutların fiziksel sırası ile ilişkilidir (Düzen'deki minor_to_major alanı), iki nokta üst üste işaretinden sonra (2,2) ise fiziksel boyutların 2x2 karoyla döşemesini belirtir.

Sezgisel olarak karolar şekli örtecek şekilde yerleştirilir ve daha sonra, yukarıdaki örnekte olduğu gibi her bir parçanın içine öğeler döşemesiz yerleştirilir. Bu örnekte, örneğin sağ kısmı bellekteki düzeni gösterir ve orijinal dizi sınırları eşit olmasa bile, tam 2x2 döşeme elde etmek için eklenen beyaz dolgu öğeleri de bulunur.

Dolgudaki fazladan öğelerin belirli bir değer içermesi gerekmez.

Bir şekil ve bloka döşeme için doğrusal dizin formülleri

Parça olmadan, d=(d_n, d_n-1, ... , d₁) (d1 en küçük boyuttur), dizi sınırlarına sahip bir dizideki e=(e_n, e_n-1, ... , e₁) şu konumda anadan küçüke doğru sıralanır:

linear_index(e; d)
= linear_index((e_n, e_n-1, ... , e₁), (d_n, d_n-1, ... , d₁))
= e_nd_n-1...d ₁ + d_n-2 d_n-1

Bu belgedeki gösterimde kolaylık sağlaması için, bir parçanın diziyle aynı sayıda boyuta sahip olduğunu varsayıyoruz. XLA'da döşeme uygulamasında bu, ilk en önemli boyutları değiştirmeden ve döşemenin yalnızca en küçük boyutlara uygulanmasıyla daha az boyutlu döşemelere genelleştirilir. Böylece belirtilen karoda, döşenen şeklin fiziksel boyutlarının son eki belirtilir.

Boyutlu parça (t_n, t_n-1, ... , t₁) kullanıldığında, dizideki dizin içeren bir öğe (e_n, e_n-1, ... , e₁), son düzende şu konuma eşlenir:

linear_index_with_tile(e, d, ⌈t


_n

Düzen iki parçadan oluştuğunu düşünebilir: (⌊e_n/t_n⌋, ... , ⌊e₁/t₁⌋); (⌈_n/t_n⌉, ... , ⌈_{n⌉, ... , ⌈t⌉, ... , ⌈d111/t1⌋). Tavan işlevi, ⌈di/ti⌉ içinde görünür çünkü karolar daha büyük dizinin sınırlarını aşarsa Şekil 1'deki gibi dolgu eklenir. Hem karolar hem de karoların içindeki öğeler, döşemesiz tekrarlı bir şekilde yerleştirilir.}

Şekil 1'deki örnekte, (2,3) öğesi (1,1,0,1) birleşik koordinat vektörü için karo dizini (1,1) ve karo içi endeksi (0,1) vardır. Parça dizinlerinin sınırları (2,3) vardır ve blokun kendisi de (2,3,2,2) birleşik vektörü için (2,2) şeklindedir. Mantıksal şekilde dizini (2,3) olan öğenin bloklu doğrusal dizin, o zaman

↗ (2,3); (3,5); (2,2))
= doğrusal_dizin((1;1;0;1); (2,3;2;2))
= doğrusal_dizin((1;1), (2,3)) ↗ 2 2 2 + 1 (doğrusal_endeks(0,1))

Dolgu-yeniden şekillendirme-transpozisyon olarak döşeme

Karo tabanlı düzen şu şekilde çalışır:
Bir dizi boyut kullanmayı düşünün (d_n, d_n-1, ... , d1) (d1, en küçük boyuttur). Boyut (t_n, t_n-1, ... , t₁) (t₁ en küçük boyuttur) döşeme ile düzenlendiğinde, bu döşeme aşağıdaki şekilde dolguyu yeniden şekillendirme bağlamında açıklanabilir.

1. Dizi, (⌈d_n/t_n⌉ özent_n, ... , ⌈d₁/t₁⌉•t₁) ile doldurulur.
2. Her boyut (⌈d_i/ti⌉, t_i) ayrı ayrı gösterilir. Diğer bir deyişle, dizi
   şeklinde yeniden şekillendirilir (⌈d_n/t_n⌉, t_n, ... , ⌈d₁/t₁⌉, t₁).
   Bu yeniden şekillendirmede tek başına fiziksel bir düzen değişikliği yoktur. Bu nedenle bu yeniden şekil bir bit yayınıdır. Kişi açık bir şekilde bir karo üzerinde düşünmüyorsa bu yeniden şekil, dolgulu şekille aynı sayıda öğeye sahip herhangi bir şekli ifade edebilir. Buradaki örnekte, bir karonun bu şekilde nasıl ifade edileceği gösterilmektedir.
3. Ters çevirme, t_n, ... , t₁'i göreli sıralarını korurken en küçük boyutlara taşıyarak gerçekleşir. Böylece boyutların en büyükten en küçüğe doğru sıralaması
   olur (⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌈d₁/t₁⌈d, 1_n).

Son şekil, her bir boyuttaki karo sayısını açıklayan
(⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉) ön ekine sahiptir. Dizideki bir öğe (e_n, ... , e₁), son şekilde bu öğeye eşlenir:
(⌊e_n/t_n⌋, ... , ⌊e₀/t₀⌋, e_n mod t_n, ... , e₁). Öğenin doğrusal dizininin, yukarıdaki formülü beklendiği gibi takip ettiğini görmek kolaydır.

Tekrarlanan parçalar

XLA'nın döşemeleri, tekrar tekrar uygulandığında daha da esnek hale gelir.

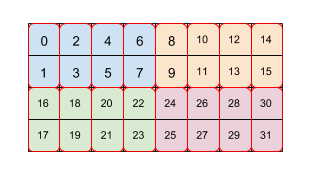
Şekil 2

Şekil 2'de, 4x8 boyutundaki bir dizinin iki döşeme düzeyine (ilk 2x4, sonra 2x1) nasıl döşendiği gösterilmektedir. Bu yinelenen parçayı (2,4)(2,1) olarak temsil ederiz. Her renk 2x4 boyutunda bir karoyu gösterirken her kırmızı kenarlık kutusu 2x1 karodur. Sayılar, söz konusu öğenin belleğindeki doğrusal dizini parçalanmış biçimde gösterir. Bu biçim, ilk karonun daha büyük olması dışında TPU'da BF16 için kullanılan biçimle eşleşir. Örneğin, döşeme (8.128)(2,1). 2x1 ile ikinci parçanın amacı, bir TPU mimarisine uygun şekilde 32 bitlik bir değer oluşturmak üzere iki 16 bit değeri toplamaktır.

İkinci veya sonraki bir parçanın, (8, 128)(2,1) işlemiyle verilen bu örnekte olduğu gibi sadece parça içindeki verileri yeniden düzenleyen,küçük parça içi boyutun her ikisine de işaret edebileceğini unutmayın. Ancak, önceki parçadaki önemli çapraz döşeme boyutlarına da işaret edebilir.

Karoları kullanarak boyutları birleştirme

XLA'nın döşemeleri, boyutları birleştirmeyi de destekler. Örneğin, (2,3) ile parçalara ayırmadan önce F32[2,7,8,11,10]{4,3,2,1,0} içindeki boyutları F32[112,110]{1,0} olarak birleştirebilir. Kullanılan karo (∗,∗,2,∗,3) şeklindedir. Burada, bir karodaki yıldız işareti, söz konusu boyutu alıp bir sonraki küçük boyutla birleştirildiği anlamına gelir. Birden çok komşu boyut tek bir boyut altında toplanabilir. Dahil edilen bir boyut, parçanın ilgili boyutunda -1 karo değeriyle temsil edilir. Bu değer, herhangi bir parçada boyut boyutu olarak geçerli değildir.

Daha kesin olarak belirtmek gerekirse, şeklin i boyutu yıldız işaretiyle kaldırılırsa, parçanın önceki tanımı uygulanmadan önce bu boyut hem döşenen şekilden hem de parça vektöründen kaldırılır ve şeklin i-1 boyutunun dizi sınırı d_i-1'den d_id_i-1'e yükseltilir. Bu adım, karo vektöründeki her bir yıldız işareti için tekrarlanır.