Warning: This project is deprecated. TensorFlow Addons has stopped development, The project will only be providing minimal maintenance releases until May 2024. See the full announcement here or on github.

TensorFlow Addons Optimizers: ConditionalGradient

View on TensorFlow.org Run in Google Colab View source on GitHub Download notebook

Overview

This notebook will demonstrate how to use the Conditional Graident Optimizer from the Addons package.

ConditionalGradient

Constraining the parameters of a neural network has been shown to be beneficial in training because of the underlying regularization effects. Often, parameters are constrained via a soft penalty (which never guarantees the constraint satisfaction) or via a projection operation (which is computationally expensive). Conditional gradient (CG) optimizer, on the other hand, enforces the constraints strictly without the need for an expensive projection step. It works by minimizing a linear approximation of the objective within the constraint set. In this notebook, you demonstrate the appliction of Frobenius norm constraint via the CG optimizer on the MNIST dataset. CG is now available as a tensorflow API. More details of the optimizer are available at https://arxiv.org/pdf/1803.06453.pdf

Setup

pip install -U tensorflow-addons

import tensorflow as tf
import tensorflow_addons as tfa
from matplotlib import pyplot as plt

# Hyperparameters
batch_size=64
epochs=10

Build the Model

model_1 = tf.keras.Sequential([
    tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
    tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
    tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])

Prep the Data

# Load MNIST dataset as NumPy arrays
dataset = {}
num_validation = 10000
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

# Preprocess the data
x_train = x_train.reshape(-1, 784).astype('float32') / 255
x_test = x_test.reshape(-1, 784).astype('float32') / 255

Define a Custom Callback Function

def frobenius_norm(m):
    """This function is to calculate the frobenius norm of the matrix of all
    layer's weight.

    Args:
        m: is a list of weights param for each layers.
    """
    total_reduce_sum = 0
    for i in range(len(m)):
        total_reduce_sum = total_reduce_sum + tf.math.reduce_sum(m[i]**2)
    norm = total_reduce_sum**0.5
    return norm

CG_frobenius_norm_of_weight = []
CG_get_weight_norm = tf.keras.callbacks.LambdaCallback(
    on_epoch_end=lambda batch, logs: CG_frobenius_norm_of_weight.append(
        frobenius_norm(model_1.trainable_weights).numpy()))

Train and Evaluate: Using CG as Optimizer

Simply replace typical keras optimizers with the new tfa optimizer 

# Compile the model
model_1.compile(
    optimizer=tfa.optimizers.ConditionalGradient(
        learning_rate=0.99949, lambda_=203),  # Utilize TFA optimizer
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    metrics=['accuracy'])

history_cg = model_1.fit(
    x_train,
    y_train,
    batch_size=batch_size,
    validation_data=(x_test, y_test),
    epochs=epochs,
    callbacks=[CG_get_weight_norm])

Epoch 1/10
938/938 [==============================] - 3s 3ms/step - loss: 0.3808 - accuracy: 0.8852 - val_loss: 0.2282 - val_accuracy: 0.9301
Epoch 2/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1941 - accuracy: 0.9417 - val_loss: 0.1697 - val_accuracy: 0.9508
Epoch 3/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1525 - accuracy: 0.9540 - val_loss: 0.1494 - val_accuracy: 0.9570
Epoch 4/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1376 - accuracy: 0.9583 - val_loss: 0.1346 - val_accuracy: 0.9600
Epoch 5/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1239 - accuracy: 0.9620 - val_loss: 0.1573 - val_accuracy: 0.9521
Epoch 6/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1187 - accuracy: 0.9641 - val_loss: 0.1538 - val_accuracy: 0.9571
Epoch 7/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1130 - accuracy: 0.9647 - val_loss: 0.1625 - val_accuracy: 0.9469
Epoch 8/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1069 - accuracy: 0.9678 - val_loss: 0.1347 - val_accuracy: 0.9576
Epoch 9/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1055 - accuracy: 0.9676 - val_loss: 0.1173 - val_accuracy: 0.9626
Epoch 10/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1049 - accuracy: 0.9678 - val_loss: 0.1102 - val_accuracy: 0.9666

Train and Evaluate: Using SGD as Optimizer

model_2 = tf.keras.Sequential([
    tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
    tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
    tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])

SGD_frobenius_norm_of_weight = []
SGD_get_weight_norm = tf.keras.callbacks.LambdaCallback(
    on_epoch_end=lambda batch, logs: SGD_frobenius_norm_of_weight.append(
        frobenius_norm(model_2.trainable_weights).numpy()))

# Compile the model
model_2.compile(
    optimizer=tf.keras.optimizers.SGD(0.01),  # Utilize SGD optimizer
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    metrics=['accuracy'])

history_sgd = model_2.fit(
    x_train,
    y_train,
    batch_size=batch_size,
    validation_data=(x_test, y_test),
    epochs=epochs,
    callbacks=[SGD_get_weight_norm])

Epoch 1/10
938/938 [==============================] - 2s 2ms/step - loss: 1.0268 - accuracy: 0.7297 - val_loss: 0.4595 - val_accuracy: 0.8765
Epoch 2/10
938/938 [==============================] - 2s 2ms/step - loss: 0.4025 - accuracy: 0.8876 - val_loss: 0.3362 - val_accuracy: 0.9062
Epoch 3/10
938/938 [==============================] - 2s 2ms/step - loss: 0.3292 - accuracy: 0.9055 - val_loss: 0.2908 - val_accuracy: 0.9182
Epoch 4/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2927 - accuracy: 0.9157 - val_loss: 0.2666 - val_accuracy: 0.9253
Epoch 5/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2668 - accuracy: 0.9230 - val_loss: 0.2495 - val_accuracy: 0.9277
Epoch 6/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2462 - accuracy: 0.9293 - val_loss: 0.2285 - val_accuracy: 0.9336
Epoch 7/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2283 - accuracy: 0.9347 - val_loss: 0.2155 - val_accuracy: 0.9371
Epoch 8/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2137 - accuracy: 0.9392 - val_loss: 0.2004 - val_accuracy: 0.9407
Epoch 9/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2002 - accuracy: 0.9428 - val_loss: 0.1957 - val_accuracy: 0.9426
Epoch 10/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1889 - accuracy: 0.9467 - val_loss: 0.1813 - val_accuracy: 0.9462

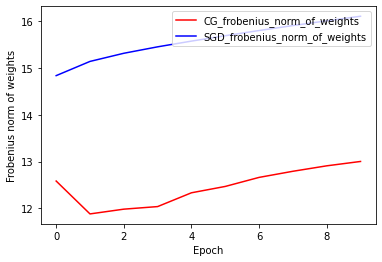
Frobenius Norm of Weights: CG vs SGD

The current implementation of CG optimizer is based on Frobenius Norm, with considering Frobenius Norm as regularizer in the target function. Therefore, you compare CG’s regularized effect with SGD optimizer, which has not imposed Frobenius Norm regularizer.

plt.plot(
    CG_frobenius_norm_of_weight,
    color='r',
    label='CG_frobenius_norm_of_weights')
plt.plot(
    SGD_frobenius_norm_of_weight,
    color='b',
    label='SGD_frobenius_norm_of_weights')
plt.xlabel('Epoch')
plt.ylabel('Frobenius norm of weights')
plt.legend(loc=1)

<matplotlib.legend.Legend at 0x7f9601c18640>

png

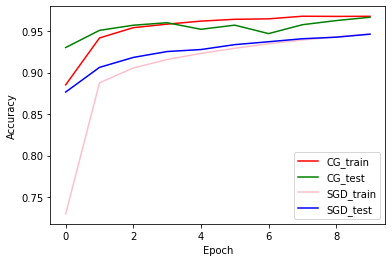
Train and Validation Accuracy: CG vs SGD

plt.plot(history_cg.history['accuracy'], color='r', label='CG_train')
plt.plot(history_cg.history['val_accuracy'], color='g', label='CG_test')
plt.plot(history_sgd.history['accuracy'], color='pink', label='SGD_train')
plt.plot(history_sgd.history['val_accuracy'], color='b', label='SGD_test')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(loc=4)

<matplotlib.legend.Legend at 0x7f95c0088ac0>

png