 View on TensorFlow.org View on TensorFlow.org
|
 Run in Google Colab Run in Google Colab
|
 View source on GitHub View source on GitHub
|
 Download notebook Download notebook
|
This tutorial demonstrates how to use Deep & Cross Network (DCN) to effectively learn feature crosses.
Background
What are feature crosses and why are they important? Imagine that we are building a recommender system to sell a blender to customers. Then, a customer's past purchase history such as purchased_bananas and purchased_cooking_books, or geographic features, are single features. If one has purchased both bananas and cooking books, then this customer will more likely click on the recommended blender. The combination of purchased_bananas and purchased_cooking_books is referred to as a feature cross, which provides additional interaction information beyond the individual features.
What are the challenges in learning feature crosses? In Web-scale applications, data are mostly categorical, leading to large and sparse feature space. Identifying effective feature crosses in this setting often requires manual feature engineering or exhaustive search. Traditional feed-forward multilayer perceptron (MLP) models are universal function approximators; however, they cannot efficiently approximate even 2nd or 3rd-order feature crosses [1, 2].
What is Deep & Cross Network (DCN)? DCN was designed to learn explicit and bounded-degree cross features more effectively. It starts with an input layer (typically an embedding layer), followed by a cross network containing multiple cross layers that models explicit feature interactions, and then combines with a deep network that models implicit feature interactions.
- Cross Network. This is the core of DCN. It explicitly applies feature crossing at each layer, and the highest
polynomial degree increases with layer depth. The following figure shows the \((i+1)\)-th cross layer.
- Deep Network. It is a traditional feedforward multilayer perceptron (MLP).
The deep network and cross network are then combined to form DCN [1]. Commonly, we could stack a deep network on top of the cross network (stacked structure); we could also place them in parallel (parallel structure).
In the following, we will first show the advantage of DCN with a toy example, and then we will walk you through some common ways to utilize DCN using the MovieLen-1M dataset.
Let's first install and import the necessary packages for this colab.
pip install -q tensorflow-recommenderspip install -q --upgrade tensorflow-datasets
import pprint
%matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
import numpy as np
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_recommenders as tfrs
2022-12-14 12:19:17.483745: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer.so.7'; dlerror: libnvinfer.so.7: cannot open shared object file: No such file or directory 2022-12-14 12:19:17.483841: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer_plugin.so.7'; dlerror: libnvinfer_plugin.so.7: cannot open shared object file: No such file or directory 2022-12-14 12:19:17.483851: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Cannot dlopen some TensorRT libraries. If you would like to use Nvidia GPU with TensorRT, please make sure the missing libraries mentioned above are installed properly.
Toy Example
To illustrate the benefits of DCN, let's work through a simple example. Suppose we have a dataset where we're trying to model the likelihood of a customer clicking on a blender Ad, with its features and label described as follows.
| Features / Label | Description | Value Type / Range |
|---|---|---|
| \(x_1\) = country | the country this customer lives in | Int in [0, 199] |
| \(x_2\) = bananas | # bananas the customer has purchased | Int in [0, 23] |
| \(x_3\) = cookbooks | # cooking books the customer has purchased | Int in [0, 5] |
| \(y\) | the likelihood of clicking on a blender Ad | -- |
Then, we let the data follow the following underlying distribution:
\[y = f(x_1, x_2, x_3) = 0.1x_1 + 0.4x_2+0.7x_3 + 0.1x_1x_2+3.1x_2x_3+0.1x_3^2\]
where the likelihood \(y\) depends linearly both on features \(x_i\)'s, but also on multiplicative interactions between the \(x_i\)'s. In our case, we would say that the likelihood of purchasing a blender (\(y\)) depends not just on buying bananas (\(x_2\)) or cookbooks (\(x_3\)), but also on buying bananas and cookbooks together (\(x_2x_3\)).
We can generate the data for this as follows:
Synthetic data generation
We first define \(f(x_1, x_2, x_3)\) as described above.
def get_mixer_data(data_size=100_000, random_seed=42):
# We need to fix the random seed
# to make colab runs repeatable.
rng = np.random.RandomState(random_seed)
country = rng.randint(200, size=[data_size, 1]) / 200.
bananas = rng.randint(24, size=[data_size, 1]) / 24.
cookbooks = rng.randint(6, size=[data_size, 1]) / 6.
x = np.concatenate([country, bananas, cookbooks], axis=1)
# # Create 1st-order terms.
y = 0.1 * country + 0.4 * bananas + 0.7 * cookbooks
# Create 2nd-order cross terms.
y += 0.1 * country * bananas + 3.1 * bananas * cookbooks + (
0.1 * cookbooks * cookbooks)
return x, y
Let's generate the data that follows the distribution, and split the data into 90% for training and 10% for testing.
x, y = get_mixer_data()
num_train = 90000
train_x = x[:num_train]
train_y = y[:num_train]
eval_x = x[num_train:]
eval_y = y[num_train:]
Model construction
We're going to try out both cross network and deep network to illustrate the advantage a cross network can bring to recommenders. As the data we just created only contains 2nd-order feature interactions, it would be sufficient to illustrate with a single-layered cross network. If we wanted to model higher-order feature interactions, we could stack multiple cross layers and use a multi-layered cross network. The two models we will be building are:
- Cross Network with only one cross layer;
- Deep Network with wider and deeper ReLU layers.
We first build a unified model class whose loss is the mean squared error.
class Model(tfrs.Model):
def __init__(self, model):
super().__init__()
self._model = model
self._logit_layer = tf.keras.layers.Dense(1)
self.task = tfrs.tasks.Ranking(
loss=tf.keras.losses.MeanSquaredError(),
metrics=[
tf.keras.metrics.RootMeanSquaredError("RMSE")
]
)
def call(self, x):
x = self._model(x)
return self._logit_layer(x)
def compute_loss(self, features, training=False):
x, labels = features
scores = self(x)
return self.task(
labels=labels,
predictions=scores,
)
Then, we specify the cross network (with 1 cross layer of size 3) and the ReLU-based DNN (with layer sizes [512, 256, 128]):
crossnet = Model(tfrs.layers.dcn.Cross())
deepnet = Model(
tf.keras.Sequential([
tf.keras.layers.Dense(512, activation="relu"),
tf.keras.layers.Dense(256, activation="relu"),
tf.keras.layers.Dense(128, activation="relu")
])
)
Model training
Now that we have the data and models ready, we are going to train the models. We first shuffle and batch the data to prepare for model training.
train_data = tf.data.Dataset.from_tensor_slices((train_x, train_y)).batch(1000)
eval_data = tf.data.Dataset.from_tensor_slices((eval_x, eval_y)).batch(1000)
Then, we define the number of epochs as well as the learning rate.
epochs = 100
learning_rate = 0.4
Alright, everything is ready now and let's compile and train the models. You could set verbose=True if you want to see how the model progresses.
crossnet.compile(optimizer=tf.keras.optimizers.Adagrad(learning_rate))
crossnet.fit(train_data, epochs=epochs, verbose=False)
<keras.callbacks.History at 0x7fc688388bb0>
deepnet.compile(optimizer=tf.keras.optimizers.Adagrad(learning_rate))
deepnet.fit(train_data, epochs=epochs, verbose=False)
<keras.callbacks.History at 0x7fc5f0386af0>
Model evaluation
We verify the model performance on the evaluation dataset and report the Root Mean Squared Error (RMSE, the lower the better).
crossnet_result = crossnet.evaluate(eval_data, return_dict=True, verbose=False)
print(f"CrossNet(1 layer) RMSE is {crossnet_result['RMSE']:.4f} "
f"using {crossnet.count_params()} parameters.")
deepnet_result = deepnet.evaluate(eval_data, return_dict=True, verbose=False)
print(f"DeepNet(large) RMSE is {deepnet_result['RMSE']:.4f} "
f"using {deepnet.count_params()} parameters.")
CrossNet(1 layer) RMSE is 0.0001 using 16 parameters. DeepNet(large) RMSE is 0.0933 using 166401 parameters.
We see that the cross network achieved magnitudes lower RMSE than a ReLU-based DNN, with magnitudes fewer parameters. This has suggested the efficieny of a cross network in learning feaure crosses.
Model understanding
We already know what feature crosses are important in our data, it would be fun to check whether our model has indeed learned the important feature cross. This can be done by visualizing the learned weight matrix in DCN. The weight \(W_{ij}\) represents the learned importance of interaction between feature \(x_i\) and \(x_j\).
mat = crossnet._model._dense.kernel
features = ["country", "purchased_bananas", "purchased_cookbooks"]
plt.figure(figsize=(9,9))
im = plt.matshow(np.abs(mat.numpy()), cmap=plt.cm.Blues)
ax = plt.gca()
divider = make_axes_locatable(plt.gca())
cax = divider.append_axes("right", size="5%", pad=0.05)
plt.colorbar(im, cax=cax)
cax.tick_params(labelsize=10)
_ = ax.set_xticklabels([''] + features, rotation=45, fontsize=10)
_ = ax.set_yticklabels([''] + features, fontsize=10)
/tmpfs/tmp/ipykernel_40470/2879280353.py:11: UserWarning: FixedFormatter should only be used together with FixedLocator _ = ax.set_xticklabels([''] + features, rotation=45, fontsize=10) /tmpfs/tmp/ipykernel_40470/2879280353.py:12: UserWarning: FixedFormatter should only be used together with FixedLocator _ = ax.set_yticklabels([''] + features, fontsize=10) <Figure size 900x900 with 0 Axes>
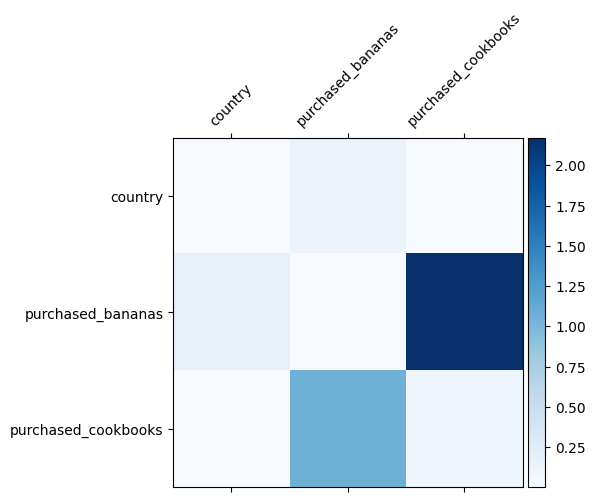
Darker colours represent stronger learned interactions - in this case, it's clear that the model learned that purchasing babanas and cookbooks together is important.
If you are interested in trying out more complicated synthetic data, feel free to check out this paper.
Movielens 1M example
We now examine the effectiveness of DCN on a real-world dataset: Movielens 1M [3]. Movielens 1M is a popular dataset for recommendation research. It predicts users' movie ratings given user-related features and movie-related features. We use this dataset to demonstrate some common ways to utilize DCN.
Data processing
The data processing procedure follows a similar procedure as the basic ranking tutorial.
ratings = tfds.load("movie_lens/100k-ratings", split="train")
ratings = ratings.map(lambda x: {
"movie_id": x["movie_id"],
"user_id": x["user_id"],
"user_rating": x["user_rating"],
"user_gender": int(x["user_gender"]),
"user_zip_code": x["user_zip_code"],
"user_occupation_text": x["user_occupation_text"],
"bucketized_user_age": int(x["bucketized_user_age"]),
})
WARNING:absl:The handle "movie_lens" for the MovieLens dataset is deprecated. Prefer using "movielens" instead. WARNING:tensorflow:From /tmpfs/src/tf_docs_env/lib/python3.9/site-packages/tensorflow/python/autograph/pyct/static_analysis/liveness.py:83: Analyzer.lamba_check (from tensorflow.python.autograph.pyct.static_analysis.liveness) is deprecated and will be removed after 2023-09-23. Instructions for updating: Lambda fuctions will be no more assumed to be used in the statement where they are used, or at least in the same block. https://github.com/tensorflow/tensorflow/issues/56089 WARNING:tensorflow:From /tmpfs/src/tf_docs_env/lib/python3.9/site-packages/tensorflow/python/autograph/pyct/static_analysis/liveness.py:83: Analyzer.lamba_check (from tensorflow.python.autograph.pyct.static_analysis.liveness) is deprecated and will be removed after 2023-09-23. Instructions for updating: Lambda fuctions will be no more assumed to be used in the statement where they are used, or at least in the same block. https://github.com/tensorflow/tensorflow/issues/56089
Next, we randomly split the data into 80% for training and 20% for testing.
tf.random.set_seed(42)
shuffled = ratings.shuffle(100_000, seed=42, reshuffle_each_iteration=False)
train = shuffled.take(80_000)
test = shuffled.skip(80_000).take(20_000)
Then, we create vocabulary for each feature.
feature_names = ["movie_id", "user_id", "user_gender", "user_zip_code",
"user_occupation_text", "bucketized_user_age"]
vocabularies = {}
for feature_name in feature_names:
vocab = ratings.batch(1_000_000).map(lambda x: x[feature_name])
vocabularies[feature_name] = np.unique(np.concatenate(list(vocab)))
Model construction
The model architecture we will be building starts with an embedding layer, which is fed into a cross network followed by a deep network. The embedding dimension is set to 32 for all the features. You could also use different embedding sizes for different features.
class DCN(tfrs.Model):
def __init__(self, use_cross_layer, deep_layer_sizes, projection_dim=None):
super().__init__()
self.embedding_dimension = 32
str_features = ["movie_id", "user_id", "user_zip_code",
"user_occupation_text"]
int_features = ["user_gender", "bucketized_user_age"]
self._all_features = str_features + int_features
self._embeddings = {}
# Compute embeddings for string features.
for feature_name in str_features:
vocabulary = vocabularies[feature_name]
self._embeddings[feature_name] = tf.keras.Sequential(
[tf.keras.layers.StringLookup(
vocabulary=vocabulary, mask_token=None),
tf.keras.layers.Embedding(len(vocabulary) + 1,
self.embedding_dimension)
])
# Compute embeddings for int features.
for feature_name in int_features:
vocabulary = vocabularies[feature_name]
self._embeddings[feature_name] = tf.keras.Sequential(
[tf.keras.layers.IntegerLookup(
vocabulary=vocabulary, mask_value=None),
tf.keras.layers.Embedding(len(vocabulary) + 1,
self.embedding_dimension)
])
if use_cross_layer:
self._cross_layer = tfrs.layers.dcn.Cross(
projection_dim=projection_dim,
kernel_initializer="glorot_uniform")
else:
self._cross_layer = None
self._deep_layers = [tf.keras.layers.Dense(layer_size, activation="relu")
for layer_size in deep_layer_sizes]
self._logit_layer = tf.keras.layers.Dense(1)
self.task = tfrs.tasks.Ranking(
loss=tf.keras.losses.MeanSquaredError(),
metrics=[tf.keras.metrics.RootMeanSquaredError("RMSE")]
)
def call(self, features):
# Concatenate embeddings
embeddings = []
for feature_name in self._all_features:
embedding_fn = self._embeddings[feature_name]
embeddings.append(embedding_fn(features[feature_name]))
x = tf.concat(embeddings, axis=1)
# Build Cross Network
if self._cross_layer is not None:
x = self._cross_layer(x)
# Build Deep Network
for deep_layer in self._deep_layers:
x = deep_layer(x)
return self._logit_layer(x)
def compute_loss(self, features, training=False):
labels = features.pop("user_rating")
scores = self(features)
return self.task(
labels=labels,
predictions=scores,
)
Model training
We shuffle, batch and cache the training and test data.
cached_train = train.shuffle(100_000).batch(8192).cache()
cached_test = test.batch(4096).cache()
Let's define a function that runs a model multiple times and returns the model's RMSE mean and standard deviation out of multiple runs.
def run_models(use_cross_layer, deep_layer_sizes, projection_dim=None, num_runs=5):
models = []
rmses = []
for i in range(num_runs):
model = DCN(use_cross_layer=use_cross_layer,
deep_layer_sizes=deep_layer_sizes,
projection_dim=projection_dim)
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate))
models.append(model)
model.fit(cached_train, epochs=epochs, verbose=False)
metrics = model.evaluate(cached_test, return_dict=True)
rmses.append(metrics["RMSE"])
mean, stdv = np.average(rmses), np.std(rmses)
return {"model": models, "mean": mean, "stdv": stdv}
We set some hyper-parameters for the models. Note that these hyper-parameters are set globally for all the models for demonstration purpose. If you want to obtain the best performance for each model, or conduct a fair comparison among models, then we'd suggest you to fine-tune the hyper-parameters. Remember that the model architecture and optimization schemes are intertwined.
epochs = 8
learning_rate = 0.01
DCN (stacked). We first train a DCN model with a stacked structure, that is, the inputs are fed to a cross network followed by a deep network.
dcn_result = run_models(use_cross_layer=True,
deep_layer_sizes=[192, 192])
WARNING:tensorflow:mask_value is deprecated, use mask_token instead. WARNING:tensorflow:mask_value is deprecated, use mask_token instead. 5/5 [==============================] - 2s 19ms/step - RMSE: 0.9322 - loss: 0.8695 - regularization_loss: 0.0000e+00 - total_loss: 0.8695 5/5 [==============================] - 0s 3ms/step - RMSE: 0.9350 - loss: 0.8744 - regularization_loss: 0.0000e+00 - total_loss: 0.8744 5/5 [==============================] - 0s 3ms/step - RMSE: 0.9303 - loss: 0.8654 - regularization_loss: 0.0000e+00 - total_loss: 0.8654 5/5 [==============================] - 0s 3ms/step - RMSE: 0.9322 - loss: 0.8695 - regularization_loss: 0.0000e+00 - total_loss: 0.8695 5/5 [==============================] - 0s 3ms/step - RMSE: 0.9333 - loss: 0.8718 - regularization_loss: 0.0000e+00 - total_loss: 0.8718
Low-rank DCN. To reduce the training and serving cost, we leverage low-rank techniques to approximate the DCN weight matrices. The rank is passed in through argument projection_dim; a smaller projection_dim results in a lower cost. Note that projection_dim needs to be smaller than (input size)/2 to reduce the cost. In practice, we've observed using low-rank DCN with rank (input size)/4 consistently preserved the accuracy of a full-rank DCN.
dcn_lr_result = run_models(use_cross_layer=True,
projection_dim=20,
deep_layer_sizes=[192, 192])
5/5 [==============================] - 0s 3ms/step - RMSE: 0.9358 - loss: 0.8761 - regularization_loss: 0.0000e+00 - total_loss: 0.8761 5/5 [==============================] - 0s 3ms/step - RMSE: 0.9349 - loss: 0.8746 - regularization_loss: 0.0000e+00 - total_loss: 0.8746 5/5 [==============================] - 0s 3ms/step - RMSE: 0.9330 - loss: 0.8715 - regularization_loss: 0.0000e+00 - total_loss: 0.8715 5/5 [==============================] - 0s 3ms/step - RMSE: 0.9300 - loss: 0.8648 - regularization_loss: 0.0000e+00 - total_loss: 0.8648 5/5 [==============================] - 0s 3ms/step - RMSE: 0.9310 - loss: 0.8672 - regularization_loss: 0.0000e+00 - total_loss: 0.8672
DNN. We train a same-sized DNN model as a reference.
dnn_result = run_models(use_cross_layer=False,
deep_layer_sizes=[192, 192, 192])
5/5 [==============================] - 0s 3ms/step - RMSE: 0.9379 - loss: 0.8803 - regularization_loss: 0.0000e+00 - total_loss: 0.8803 5/5 [==============================] - 0s 3ms/step - RMSE: 0.9303 - loss: 0.8660 - regularization_loss: 0.0000e+00 - total_loss: 0.8660 5/5 [==============================] - 0s 3ms/step - RMSE: 0.9384 - loss: 0.8814 - regularization_loss: 0.0000e+00 - total_loss: 0.8814 5/5 [==============================] - 0s 3ms/step - RMSE: 0.9362 - loss: 0.8771 - regularization_loss: 0.0000e+00 - total_loss: 0.8771 5/5 [==============================] - 0s 3ms/step - RMSE: 0.9324 - loss: 0.8706 - regularization_loss: 0.0000e+00 - total_loss: 0.8706
We evaluate the model on test data and report the mean and standard deviation out of 5 runs.
print("DCN RMSE mean: {:.4f}, stdv: {:.4f}".format(
dcn_result["mean"], dcn_result["stdv"]))
print("DCN (low-rank) RMSE mean: {:.4f}, stdv: {:.4f}".format(
dcn_lr_result["mean"], dcn_lr_result["stdv"]))
print("DNN RMSE mean: {:.4f}, stdv: {:.4f}".format(
dnn_result["mean"], dnn_result["stdv"]))
DCN RMSE mean: 0.9326, stdv: 0.0015 DCN (low-rank) RMSE mean: 0.9329, stdv: 0.0022 DNN RMSE mean: 0.9350, stdv: 0.0032
We see that DCN achieved better performance than a same-sized DNN with ReLU layers. Moreover, the low-rank DCN was able to reduce parameters while maintaining the accuracy.
More on DCN. Besides what've been demonstrated above, there are more creative yet practically useful ways to utilize DCN [1].
DCN with a parallel structure. The inputs are fed in parallel to a cross network and a deep network.
Concatenating cross layers. The inputs are fed in parallel to multiple cross layers to capture complementary feature crosses.
Model understanding
The weight matrix \(W\) in DCN reveals what feature crosses the model has learned to be important. Recall that in the previous toy example, the importance of interactions between the \(i\)-th and \(j\)-th features is captured by the (\(i, j\))-th element of \(W\).
What's a bit different here is that the feature embeddings are of size 32 instead of size 1. Hence, the importance will be characterized by the \((i, j)\)-th block \(W_{i,j}\) which is of dimension 32 by 32. In the following, we visualize the Frobenius norm [4] \(||W_{i,j}||_F\) of each block, and a larger norm would suggest higher importance (assuming the features' embeddings are of similar scales).
Besides block norm, we could also visualize the entire matrix, or the mean/median/max value of each block.
model = dcn_result["model"][0]
mat = model._cross_layer._dense.kernel
features = model._all_features
block_norm = np.ones([len(features), len(features)])
dim = model.embedding_dimension
# Compute the norms of the blocks.
for i in range(len(features)):
for j in range(len(features)):
block = mat[i * dim:(i + 1) * dim,
j * dim:(j + 1) * dim]
block_norm[i,j] = np.linalg.norm(block, ord="fro")
plt.figure(figsize=(9,9))
im = plt.matshow(block_norm, cmap=plt.cm.Blues)
ax = plt.gca()
divider = make_axes_locatable(plt.gca())
cax = divider.append_axes("right", size="5%", pad=0.05)
plt.colorbar(im, cax=cax)
cax.tick_params(labelsize=10)
_ = ax.set_xticklabels([""] + features, rotation=45, ha="left", fontsize=10)
_ = ax.set_yticklabels([""] + features, fontsize=10)
/tmpfs/tmp/ipykernel_40470/1244897914.py:23: UserWarning: FixedFormatter should only be used together with FixedLocator _ = ax.set_xticklabels([""] + features, rotation=45, ha="left", fontsize=10) /tmpfs/tmp/ipykernel_40470/1244897914.py:24: UserWarning: FixedFormatter should only be used together with FixedLocator _ = ax.set_yticklabels([""] + features, fontsize=10) <Figure size 900x900 with 0 Axes>
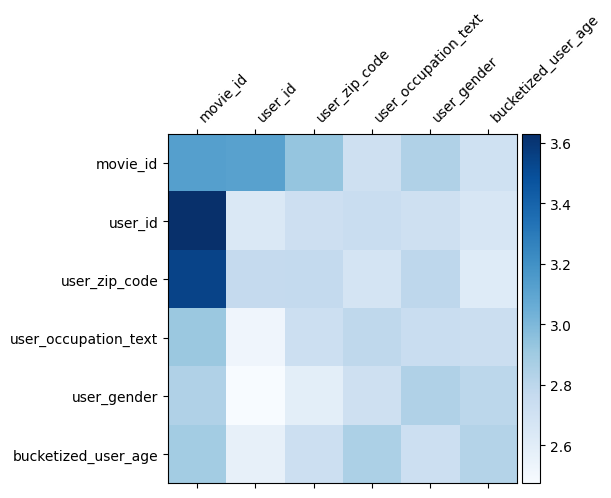
That's all for this colab! We hope that you have enjoyed learning some basics of DCN and common ways to utilize it. If you are interested in learning more, you could check out two relevant papers: DCN-v1-paper, DCN-v2-paper.
References
DCN V2: Improved Deep & Cross Network and Practical Lessons for Web-scale Learning to Rank Systems.
Ruoxi Wang, Rakesh Shivanna, Derek Zhiyuan Cheng, Sagar Jain, Dong Lin, Lichan Hong, Ed Chi. (2020)
Deep & Cross Network for Ad Click Predictions.
Ruoxi Wang, Bin Fu, Gang Fu, Mingliang Wang. (AdKDD 2017)
