Copyright 2023 The TF-Agents Authors.
View on TensorFlow.org
|
Run in Google Colab
|
View source on GitHub
|
 Download notebook
|
Introduction
This example shows how to train a Categorical DQN (C51) agent on the Cartpole environment using the TF-Agents library.
Make sure you take a look through the DQN tutorial as a prerequisite. This tutorial will assume familiarity with the DQN tutorial; it will mainly focus on the differences between DQN and C51.
Setup
If you haven't installed tf-agents yet, run:
sudo apt-get updatesudo apt-get install -y xvfb ffmpeg freeglut3-devpip install 'imageio==2.4.0'pip install pyvirtualdisplaypip install tf-agentspip install pyglet
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import base64
import imageio
import IPython
import matplotlib
import matplotlib.pyplot as plt
import PIL.Image
import pyvirtualdisplay
import tensorflow as tf
from tf_agents.agents.categorical_dqn import categorical_dqn_agent
from tf_agents.drivers import dynamic_step_driver
from tf_agents.environments import suite_gym
from tf_agents.environments import tf_py_environment
from tf_agents.eval import metric_utils
from tf_agents.metrics import tf_metrics
from tf_agents.networks import categorical_q_network
from tf_agents.policies import random_tf_policy
from tf_agents.replay_buffers import tf_uniform_replay_buffer
from tf_agents.trajectories import trajectory
from tf_agents.utils import common
# Set up a virtual display for rendering OpenAI gym environments.
display = pyvirtualdisplay.Display(visible=0, size=(1400, 900)).start()
Hyperparameters
env_name = "CartPole-v1" # @param {type:"string"}
num_iterations = 15000 # @param {type:"integer"}
initial_collect_steps = 1000 # @param {type:"integer"}
collect_steps_per_iteration = 1 # @param {type:"integer"}
replay_buffer_capacity = 100000 # @param {type:"integer"}
fc_layer_params = (100,)
batch_size = 64 # @param {type:"integer"}
learning_rate = 1e-3 # @param {type:"number"}
gamma = 0.99
log_interval = 200 # @param {type:"integer"}
num_atoms = 51 # @param {type:"integer"}
min_q_value = -20 # @param {type:"integer"}
max_q_value = 20 # @param {type:"integer"}
n_step_update = 2 # @param {type:"integer"}
num_eval_episodes = 10 # @param {type:"integer"}
eval_interval = 1000 # @param {type:"integer"}
Environment
Load the environment as before, with one for training and one for evaluation. Here we use CartPole-v1 (vs. CartPole-v0 in the DQN tutorial), which has a larger max reward of 500 rather than 200.
train_py_env = suite_gym.load(env_name)
eval_py_env = suite_gym.load(env_name)
train_env = tf_py_environment.TFPyEnvironment(train_py_env)
eval_env = tf_py_environment.TFPyEnvironment(eval_py_env)
Agent
C51 is a Q-learning algorithm based on DQN. Like DQN, it can be used on any environment with a discrete action space.
The main difference between C51 and DQN is that rather than simply predicting the Q-value for each state-action pair, C51 predicts a histogram model for the probability distribution of the Q-value:
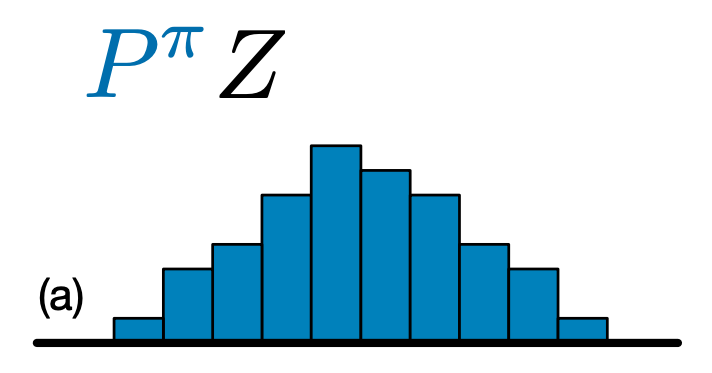
By learning the distribution rather than simply the expected value, the algorithm is able to stay more stable during training, leading to improved final performance. This is particularly true in situations with bimodal or even multimodal value distributions, where a single average does not provide an accurate picture.
In order to train on probability distributions rather than on values, C51 must perform some complex distributional computations in order to calculate its loss function. But don't worry, all of this is taken care of for you in TF-Agents!
To create a C51 Agent, we first need to create a CategoricalQNetwork. The API of the CategoricalQNetwork is the same as that of the QNetwork, except that there is an additional argument num_atoms. This represents the number of support points in our probability distribution estimates. (The above image includes 10 support points, each represented by a vertical blue bar.) As you can tell from the name, the default number of atoms is 51.
categorical_q_net = categorical_q_network.CategoricalQNetwork(
train_env.observation_spec(),
train_env.action_spec(),
num_atoms=num_atoms,
fc_layer_params=fc_layer_params)
We also need an optimizer to train the network we just created, and a train_step_counter variable to keep track of how many times the network was updated.
Note that one other significant difference from vanilla DqnAgent is that we now need to specify min_q_value and max_q_value as arguments. These specify the most extreme values of the support (in other words, the most extreme of the 51 atoms on either side). Make sure to choose these appropriately for your particular environment. Here we use -20 and 20.
optimizer = tf.compat.v1.train.AdamOptimizer(learning_rate=learning_rate)
train_step_counter = tf.Variable(0)
agent = categorical_dqn_agent.CategoricalDqnAgent(
train_env.time_step_spec(),
train_env.action_spec(),
categorical_q_network=categorical_q_net,
optimizer=optimizer,
min_q_value=min_q_value,
max_q_value=max_q_value,
n_step_update=n_step_update,
td_errors_loss_fn=common.element_wise_squared_loss,
gamma=gamma,
train_step_counter=train_step_counter)
agent.initialize()
One last thing to note is that we also added an argument to use n-step updates with \(n\) = 2. In single-step Q-learning (\(n\) = 1), we only compute the error between the Q-values at the current time step and the next time step using the single-step return (based on the Bellman optimality equation). The single-step return is defined as:
\(G_t = R_{t + 1} + \gamma V(s_{t + 1})\)
where we define \(V(s) = \max_a{Q(s, a)}\).
N-step updates involve expanding the standard single-step return function \(n\) times:
\(G_t^n = R_{t + 1} + \gamma R_{t + 2} + \gamma^2 R_{t + 3} + \dots + \gamma^n V(s_{t + n})\)
N-step updates enable the agent to bootstrap from further in the future, and with the right value of \(n\), this often leads to faster learning.
Although C51 and n-step updates are often combined with prioritized replay to form the core of the Rainbow agent, we saw no measurable improvement from implementing prioritized replay. Moreover, we find that when combining our C51 agent with n-step updates alone, our agent performs as well as other Rainbow agents on the sample of Atari environments we've tested.
Metrics and Evaluation
The most common metric used to evaluate a policy is the average return. The return is the sum of rewards obtained while running a policy in an environment for an episode, and we usually average this over a few episodes. We can compute the average return metric as follows.
def compute_avg_return(environment, policy, num_episodes=10):
total_return = 0.0
for _ in range(num_episodes):
time_step = environment.reset()
episode_return = 0.0
while not time_step.is_last():
action_step = policy.action(time_step)
time_step = environment.step(action_step.action)
episode_return += time_step.reward
total_return += episode_return
avg_return = total_return / num_episodes
return avg_return.numpy()[0]
random_policy = random_tf_policy.RandomTFPolicy(train_env.time_step_spec(),
train_env.action_spec())
compute_avg_return(eval_env, random_policy, num_eval_episodes)
# Please also see the metrics module for standard implementations of different
# metrics.
29.5
Data Collection
As in the DQN tutorial, set up the replay buffer and the initial data collection with the random policy.
replay_buffer = tf_uniform_replay_buffer.TFUniformReplayBuffer(
data_spec=agent.collect_data_spec,
batch_size=train_env.batch_size,
max_length=replay_buffer_capacity)
def collect_step(environment, policy):
time_step = environment.current_time_step()
action_step = policy.action(time_step)
next_time_step = environment.step(action_step.action)
traj = trajectory.from_transition(time_step, action_step, next_time_step)
# Add trajectory to the replay buffer
replay_buffer.add_batch(traj)
for _ in range(initial_collect_steps):
collect_step(train_env, random_policy)
# This loop is so common in RL, that we provide standard implementations of
# these. For more details see the drivers module.
# Dataset generates trajectories with shape [BxTx...] where
# T = n_step_update + 1.
dataset = replay_buffer.as_dataset(
num_parallel_calls=3, sample_batch_size=batch_size,
num_steps=n_step_update + 1).prefetch(3)
iterator = iter(dataset)
WARNING:tensorflow:From /tmpfs/src/tf_docs_env/lib/python3.9/site-packages/tf_agents/replay_buffers/tf_uniform_replay_buffer.py:342: CounterV2 (from tensorflow.python.data.experimental.ops.counter) is deprecated and will be removed in a future version. Instructions for updating: Use `tf.data.Dataset.counter(...)` instead. WARNING:tensorflow:From /tmpfs/src/tf_docs_env/lib/python3.9/site-packages/tensorflow/python/autograph/impl/api.py:377: ReplayBuffer.get_next (from tf_agents.replay_buffers.replay_buffer) is deprecated and will be removed in a future version. Instructions for updating: Use `as_dataset(..., single_deterministic_pass=False) instead.
Training the agent
The training loop involves both collecting data from the environment and optimizing the agent's networks. Along the way, we will occasionally evaluate the agent's policy to see how we are doing.
The following will take ~7 minutes to run.
try:
%%time
except:
pass
# (Optional) Optimize by wrapping some of the code in a graph using TF function.
agent.train = common.function(agent.train)
# Reset the train step
agent.train_step_counter.assign(0)
# Evaluate the agent's policy once before training.
avg_return = compute_avg_return(eval_env, agent.policy, num_eval_episodes)
returns = [avg_return]
for _ in range(num_iterations):
# Collect a few steps using collect_policy and save to the replay buffer.
for _ in range(collect_steps_per_iteration):
collect_step(train_env, agent.collect_policy)
# Sample a batch of data from the buffer and update the agent's network.
experience, unused_info = next(iterator)
train_loss = agent.train(experience)
step = agent.train_step_counter.numpy()
if step % log_interval == 0:
print('step = {0}: loss = {1}'.format(step, train_loss.loss))
if step % eval_interval == 0:
avg_return = compute_avg_return(eval_env, agent.policy, num_eval_episodes)
print('step = {0}: Average Return = {1:.2f}'.format(step, avg_return))
returns.append(avg_return)
WARNING:tensorflow:From /tmpfs/src/tf_docs_env/lib/python3.9/site-packages/tensorflow/python/util/dispatch.py:1176: calling foldr_v2 (from tensorflow.python.ops.functional_ops) with back_prop=False is deprecated and will be removed in a future version. Instructions for updating: back_prop=False is deprecated. Consider using tf.stop_gradient instead. Instead of: results = tf.foldr(fn, elems, back_prop=False) Use: results = tf.nest.map_structure(tf.stop_gradient, tf.foldr(fn, elems)) step = 200: loss = 3.189603805541992 step = 400: loss = 2.3770298957824707 step = 600: loss = 1.9695230722427368 step = 800: loss = 1.6382858753204346 step = 1000: loss = 1.640347957611084 step = 1000: Average Return = 491.70 step = 1200: loss = 1.3662605285644531 step = 1400: loss = 1.2627944946289062 step = 1600: loss = 1.091010570526123 step = 1800: loss = 1.0421620607376099 step = 2000: loss = 0.9967061281204224 step = 2000: Average Return = 168.90 step = 2200: loss = 0.9895737171173096 step = 2400: loss = 0.9468974471092224 step = 2600: loss = 0.896358072757721 step = 2800: loss = 0.8432101011276245 step = 3000: loss = 0.8755940198898315 step = 3000: Average Return = 136.70 step = 3200: loss = 0.8091744184494019 step = 3400: loss = 0.6782629489898682 step = 3600: loss = 0.6921717524528503 step = 3800: loss = 0.7346455454826355 step = 4000: loss = 0.6745090484619141 step = 4000: Average Return = 380.00 step = 4200: loss = 0.6984972953796387 step = 4400: loss = 0.561363697052002 step = 4600: loss = 0.6355947256088257 step = 4800: loss = 0.6966433525085449 step = 5000: loss = 0.7179740071296692 step = 5000: Average Return = 377.80 step = 5200: loss = 0.563409149646759 step = 5400: loss = 0.6353570222854614 step = 5600: loss = 0.47607141733169556 step = 5800: loss = 0.6655551791191101 step = 6000: loss = 0.6231980919837952 step = 6000: Average Return = 382.40 step = 6200: loss = 0.6022371053695679 step = 6400: loss = 0.4370470643043518 step = 6600: loss = 0.5686420798301697 step = 6800: loss = 0.4489099979400635 step = 7000: loss = 0.4366820454597473 step = 7000: Average Return = 255.30 step = 7200: loss = 0.6621994376182556 step = 7400: loss = 0.6025552749633789 step = 7600: loss = 0.5020204782485962 step = 7800: loss = 0.4125787913799286 step = 8000: loss = 0.470950722694397 step = 8000: Average Return = 431.40 step = 8200: loss = 0.41869550943374634 step = 8400: loss = 0.6263928413391113 step = 8600: loss = 0.5732796788215637 step = 8800: loss = 0.40630561113357544 step = 9000: loss = 0.5073099732398987 step = 9000: Average Return = 453.20 step = 9200: loss = 0.34092995524406433 step = 9400: loss = 0.33134883642196655 step = 9600: loss = 0.492952823638916 step = 9800: loss = 0.32983410358428955 step = 10000: loss = 0.6636049747467041 step = 10000: Average Return = 472.10 step = 10200: loss = 0.48846304416656494 step = 10400: loss = 0.3939424157142639 step = 10600: loss = 0.30336079001426697 step = 10800: loss = 0.26912710070610046 step = 11000: loss = 0.29472559690475464 step = 11000: Average Return = 475.90 step = 11200: loss = 0.3303176164627075 step = 11400: loss = 0.32231605052948 step = 11600: loss = 0.35834237933158875 step = 11800: loss = 0.378772497177124 step = 12000: loss = 0.3838456869125366 step = 12000: Average Return = 408.30 step = 12200: loss = 0.2626791000366211 step = 12400: loss = 0.327068567276001 step = 12600: loss = 0.3905017077922821 step = 12800: loss = 0.32192274928092957 step = 13000: loss = 0.313429594039917 step = 13000: Average Return = 500.00 step = 13200: loss = 0.3589685559272766 step = 13400: loss = 0.30565086007118225 step = 13600: loss = 0.2470700740814209 step = 13800: loss = 0.16855518519878387 step = 14000: loss = 0.25904375314712524 step = 14000: Average Return = 439.00 step = 14200: loss = 0.347642183303833 step = 14400: loss = 0.20726372301578522 step = 14600: loss = 0.2598506510257721 step = 14800: loss = 0.18607890605926514 step = 15000: loss = 0.264817476272583 step = 15000: Average Return = 457.30
Visualization
Plots
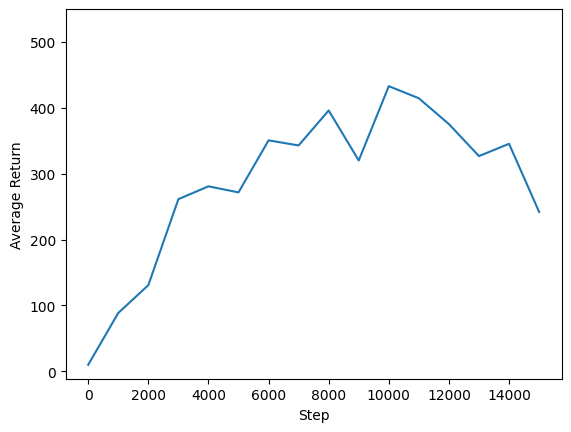
We can plot return vs global steps to see the performance of our agent. In Cartpole-v1, the environment gives a reward of +1 for every time step the pole stays up, and since the maximum number of steps is 500, the maximum possible return is also 500.
steps = range(0, num_iterations + 1, eval_interval)
plt.plot(steps, returns)
plt.ylabel('Average Return')
plt.xlabel('Step')
plt.ylim(top=550)
(22.460000801086423, 550.0)
Videos
It is helpful to visualize the performance of an agent by rendering the environment at each step. Before we do that, let us first create a function to embed videos in this colab.
def embed_mp4(filename):
"""Embeds an mp4 file in the notebook."""
video = open(filename,'rb').read()
b64 = base64.b64encode(video)
tag = '''
<video width="640" height="480" controls>
<source src="data:video/mp4;base64,{0}" type="video/mp4">
Your browser does not support the video tag.
</video>'''.format(b64.decode())
return IPython.display.HTML(tag)
The following code visualizes the agent's policy for a few episodes:
num_episodes = 3
video_filename = 'imageio.mp4'
with imageio.get_writer(video_filename, fps=60) as video:
for _ in range(num_episodes):
time_step = eval_env.reset()
video.append_data(eval_py_env.render())
while not time_step.is_last():
action_step = agent.policy.action(time_step)
time_step = eval_env.step(action_step.action)
video.append_data(eval_py_env.render())
embed_mp4(video_filename)
WARNING:root:IMAGEIO FFMPEG_WRITER WARNING: input image is not divisible by macro_block_size=16, resizing from (400, 600) to (400, 608) to ensure video compatibility with most codecs and players. To prevent resizing, make your input image divisible by the macro_block_size or set the macro_block_size to None (risking incompatibility). You may also see a FFMPEG warning concerning speedloss due to data not being aligned. [swscaler @ 0x557a47a3a880] Warning: data is not aligned! This can lead to a speed loss
C51 tends to do slightly better than DQN on CartPole-v1, but the difference between the two agents becomes more and more significant in increasingly complex environments. For example, on the full Atari 2600 benchmark, C51 demonstrates a mean score improvement of 126% over DQN after normalizing with respect to a random agent. Additional improvements can be gained by including n-step updates.
For a deeper dive into the C51 algorithm, see A Distributional Perspective on Reinforcement Learning (2017).