Нейронное структурированное обучение (NSL) фокусируется на обучении глубоких нейронных сетей путем использования структурированных сигналов (если они доступны) вместе с входными функциями. Как было представлено Bui et al. (WSDM'18) эти структурированные сигналы используются для регуляризации обучения нейронной сети, заставляя модель обучаться точным предсказаниям (за счет минимизации контролируемых потерь), и в то же время сохраняя структурное сходство входных данных (за счет минимизации потерь соседей). , см. рисунок ниже). Этот метод является универсальным и может применяться к произвольным нейронным архитектурам (таким как NN с прямой связью, сверточные NN и рекуррентные NN).
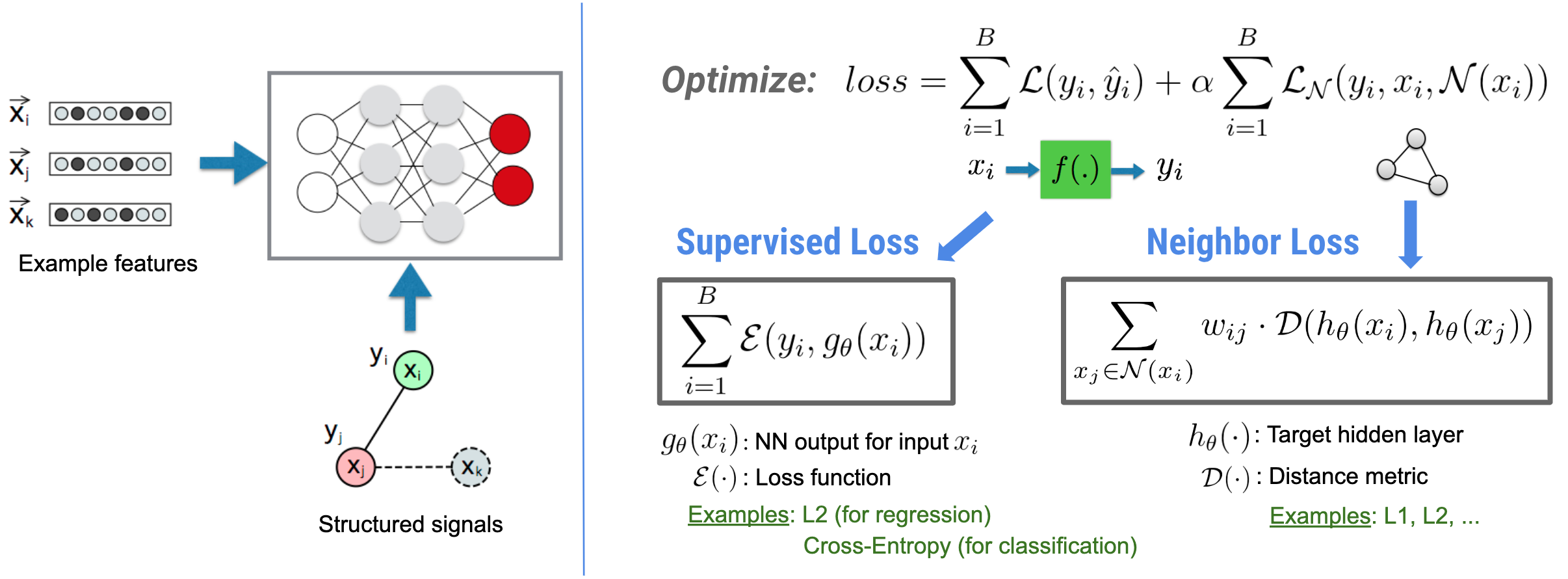
Обратите внимание, что обобщенное уравнение потерь соседей является гибким и может иметь другие формы, помимо проиллюстрированной выше. Например, мы также можем выбрать\(\sum_{x_j \in \mathcal{N}(x_i)}\mathcal{E}(y_i,g_\theta(x_j))\) быть потерей соседа, которая вычисляет расстояние между основной истиной \(y_i\)и предсказание соседа \(g_\theta(x_j)\). Это обычно используется в состязательном обучении (Goodfellow et al., ICLR'15) . Таким образом, NSL обобщается на обучение нейронных графов , если соседи явно представлены графом, и на состязательное обучение, если соседи неявно индуцируются состязательными возмущениями.
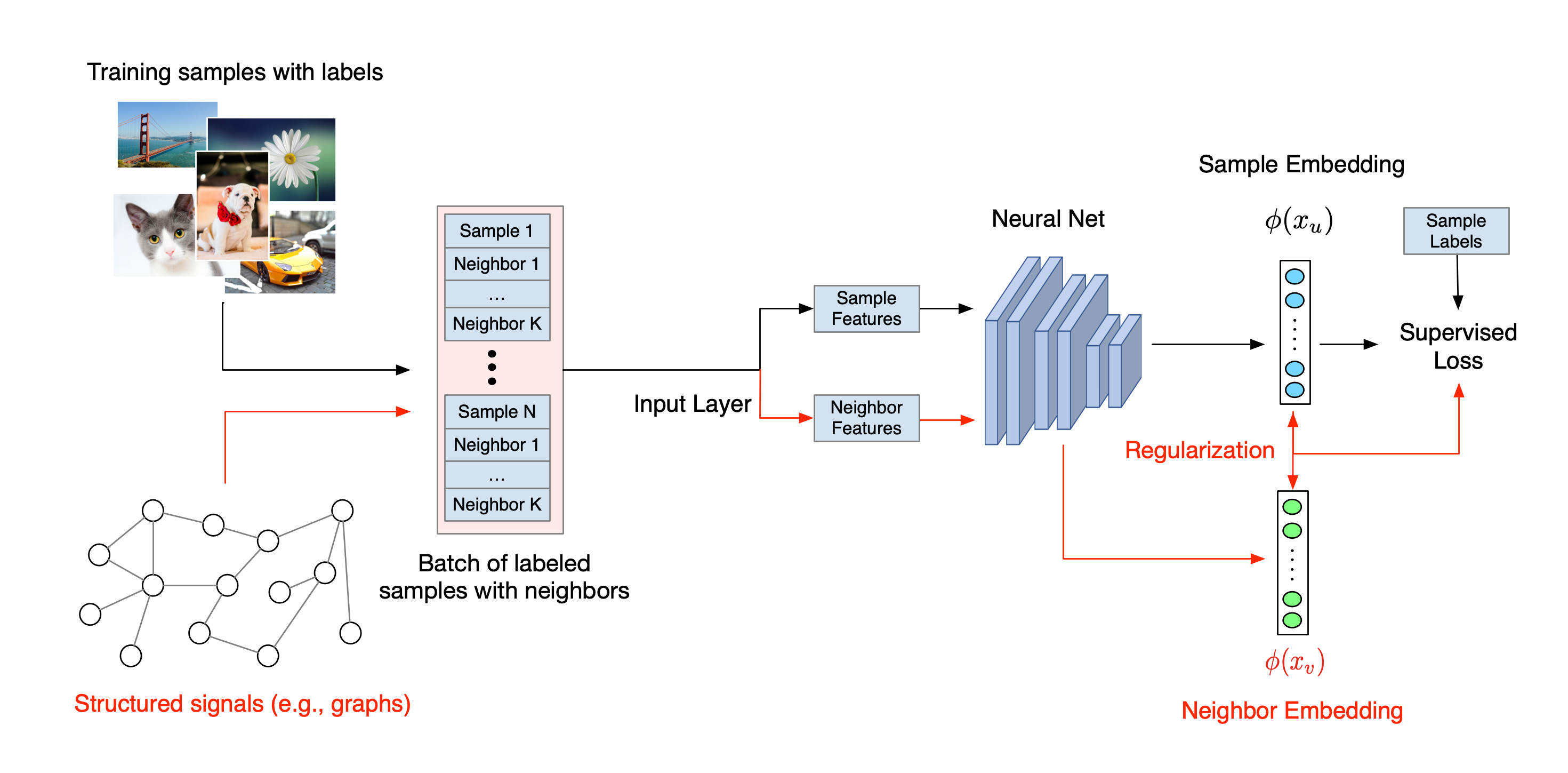
Общий рабочий процесс нейронного структурированного обучения показан ниже. Черные стрелки представляют традиционный рабочий процесс обучения, а красные стрелки представляют новый рабочий процесс, представленный NSL для использования структурированных сигналов. Во-первых, обучающие выборки дополняются структурированными сигналами. Когда структурированные сигналы не предоставляются явно, их можно либо сконструировать, либо индуцировать (последнее применимо к состязательному обучению). Затем расширенные обучающие выборки (включая как исходные выборки, так и их соответствующих соседей) передаются в нейронную сеть для расчета их вложений. Расстояние между внедрением выборки и внедрением его соседа рассчитывается и используется как потеря соседа, которая рассматривается как член регуляризации и добавляется к окончательным потерям. Для явной регуляризации на основе соседей мы обычно вычисляем потерю соседей как расстояние между внедрением выборки и внедрением соседа. Однако для вычисления потерь соседей можно использовать любой уровень нейронной сети. С другой стороны, для индуцированной регуляризации на основе соседей (состязательной) мы вычисляем потерю соседей как расстояние между выходным предсказанием индуцированного состязательного соседа и основной истинной меткой.
Зачем использовать NSL?
NSL имеет следующие преимущества:
- Более высокая точность : структурированные сигналы среди выборок могут предоставлять информацию, которая не всегда доступна во входных данных объекта; поэтому было показано, что подход к совместному обучению (как со структурированными сигналами, так и с функциями) превосходит многие существующие методы (которые основаны на обучении только с использованием функций) для широкого круга задач, таких как классификация документов и классификация семантических намерений ( Bui et al. ., WSDM'18 и Кипф и др., ICLR'17 ).
- Устойчивость : было показано, что модели, обученные на состязательных примерах, устойчивы к состязательным возмущениям, призванным ввести в заблуждение прогноз или классификацию модели ( Goodfellow et al., ICLR'15 и Miyato et al., ICLR'16 ). Когда количество обучающих выборок невелико, обучение на состязательных примерах также помогает повысить точность модели ( Ципрас и др., ICLR'19 ).
- Требуется меньше размеченных данных : NSL позволяет нейронным сетям использовать как размеченные, так и неразмеченные данные, что расширяет парадигму обучения до полуконтролируемого обучения . В частности, NSL позволяет сети обучаться с использованием помеченных данных, как в контролируемой настройке, и в то же время заставляет сеть изучать аналогичные скрытые представления для «соседних образцов», которые могут иметь или не иметь метки. Этот метод показал большие перспективы для повышения точности модели, когда объем размеченных данных относительно невелик ( Bui et al., WSDM'18 и Miyato et al., ICLR'16 ).
Пошаговые руководства
Чтобы получить практический опыт работы с нейронным структурированным обучением, у нас есть учебные пособия, охватывающие различные сценарии, в которых структурированные сигналы могут быть явно заданы, созданы или вызваны. Вот некоторые из них:
Регуляризация графов для классификации документов с использованием естественных графов . В этом уроке мы исследуем использование регуляризации графа для классификации документов, образующих естественный (органический) граф.
Регуляризация графов для классификации настроений с использованием синтезированных графиков . В этом уроке мы демонстрируем использование регуляризации графов для классификации настроений в обзорах фильмов путем построения (синтеза) структурированных сигналов.
Состязательное обучение для классификации изображений . В этом уроке мы исследуем использование состязательного обучения (при котором индуцируются структурированные сигналы) для классификации изображений, содержащих числовые цифры.
Дополнительные примеры и руководства можно найти в каталоге примеров нашего репозитория GitHub.
,Нейронное структурированное обучение (NSL) фокусируется на обучении глубоких нейронных сетей путем использования структурированных сигналов (если они доступны) вместе с входными функциями. Как было представлено Bui et al. (WSDM'18) , эти структурированные сигналы используются для регуляризации обучения нейронной сети, заставляя модель изучать точные прогнозы (за счет минимизации контролируемых потерь), и в то же время сохраняя структурное сходство входных данных (за счет минимизации потерь соседей). , см. рисунок ниже). Этот метод является универсальным и может применяться к произвольным нейронным архитектурам (таким как NN с прямой связью, сверточные NN и рекуррентные NN).

Обратите внимание, что обобщенное уравнение потерь соседей является гибким и может иметь другие формы, помимо проиллюстрированной выше. Например, мы также можем выбрать\(\sum_{x_j \in \mathcal{N}(x_i)}\mathcal{E}(y_i,g_\theta(x_j))\) быть потерей соседа, которая вычисляет расстояние между основной истиной \(y_i\)и предсказание соседа \(g_\theta(x_j)\). Это обычно используется в состязательном обучении (Goodfellow et al., ICLR'15) . Таким образом, NSL обобщается на обучение нейронных графов , если соседи явно представлены графом, и на состязательное обучение, если соседи неявно индуцируются состязательными возмущениями.
Общий рабочий процесс нейронного структурированного обучения показан ниже. Черные стрелки представляют традиционный рабочий процесс обучения, а красные стрелки представляют новый рабочий процесс, представленный NSL для использования структурированных сигналов. Во-первых, обучающие выборки дополняются структурированными сигналами. Когда структурированные сигналы не предоставляются явно, их можно либо сконструировать, либо индуцировать (последнее применимо к состязательному обучению). Затем расширенные обучающие выборки (включая как исходные выборки, так и их соответствующих соседей) передаются в нейронную сеть для расчета их вложений. Расстояние между внедрением выборки и внедрением его соседа рассчитывается и используется как потеря соседа, которая рассматривается как член регуляризации и добавляется к окончательным потерям. Для явной регуляризации на основе соседей мы обычно вычисляем потерю соседей как расстояние между внедрением выборки и внедрением соседа. Однако для вычисления потерь соседей можно использовать любой уровень нейронной сети. С другой стороны, для индуцированной регуляризации на основе соседей (состязательной) мы вычисляем потерю соседей как расстояние между выходным предсказанием индуцированного состязательного соседа и основной истинной меткой.

Зачем использовать NSL?
NSL имеет следующие преимущества:
- Более высокая точность : структурированные сигналы среди выборок могут предоставлять информацию, которая не всегда доступна во входных данных объекта; поэтому было показано, что подход к совместному обучению (как со структурированными сигналами, так и с функциями) превосходит многие существующие методы (которые основаны на обучении только с использованием функций) для широкого круга задач, таких как классификация документов и классификация семантических намерений ( Bui et al. ., WSDM'18 и Кипф и др., ICLR'17 ).
- Устойчивость : было показано, что модели, обученные на состязательных примерах, устойчивы к состязательным возмущениям, призванным ввести в заблуждение прогноз или классификацию модели ( Goodfellow et al., ICLR'15 и Miyato et al., ICLR'16 ). Когда количество обучающих выборок невелико, обучение на состязательных примерах также помогает повысить точность модели ( Ципрас и др., ICLR'19 ).
- Требуется меньше размеченных данных : NSL позволяет нейронным сетям использовать как размеченные, так и неразмеченные данные, что расширяет парадигму обучения до полуконтролируемого обучения . В частности, NSL позволяет сети обучаться с использованием помеченных данных, как в контролируемой настройке, и в то же время заставляет сеть изучать аналогичные скрытые представления для «соседних образцов», которые могут иметь или не иметь метки. Этот метод показал большие перспективы для повышения точности модели, когда объем размеченных данных относительно невелик ( Bui et al., WSDM'18 и Miyato et al., ICLR'16 ).
Пошаговые руководства
Чтобы получить практический опыт работы с нейронным структурированным обучением, у нас есть учебные пособия, охватывающие различные сценарии, в которых структурированные сигналы могут быть явно заданы, созданы или вызваны. Вот некоторые из них:
Регуляризация графов для классификации документов с использованием естественных графов . В этом уроке мы исследуем использование регуляризации графа для классификации документов, образующих естественный (органический) граф.
Регуляризация графов для классификации настроений с использованием синтезированных графиков . В этом уроке мы демонстрируем использование регуляризации графов для классификации настроений в обзорах фильмов путем построения (синтеза) структурированных сигналов.
Состязательное обучение для классификации изображений . В этом уроке мы исследуем использование состязательного обучения (при котором индуцируются структурированные сигналы) для классификации изображений, содержащих числовые цифры.
Дополнительные примеры и руководства можно найти в каталоге примеров нашего репозитория GitHub.
,Нейронное структурированное обучение (NSL) фокусируется на обучении глубоких нейронных сетей путем использования структурированных сигналов (если они доступны) вместе с входными функциями. Как было представлено Bui et al. (WSDM'18) эти структурированные сигналы используются для регуляризации обучения нейронной сети, заставляя модель обучаться точным предсказаниям (за счет минимизации контролируемых потерь), и в то же время сохраняя структурное сходство входных данных (за счет минимизации потерь соседей). , см. рисунок ниже). Этот метод является универсальным и может применяться к произвольным нейронным архитектурам (таким как NN с прямой связью, сверточные NN и рекуррентные NN).

Обратите внимание, что обобщенное уравнение потерь соседей является гибким и может иметь другие формы, помимо проиллюстрированной выше. Например, мы также можем выбрать\(\sum_{x_j \in \mathcal{N}(x_i)}\mathcal{E}(y_i,g_\theta(x_j))\) быть потерей соседа, которая вычисляет расстояние между основной истиной \(y_i\)и предсказание соседа \(g_\theta(x_j)\). Это обычно используется в состязательном обучении (Goodfellow et al., ICLR'15) . Таким образом, NSL обобщается на обучение нейронных графов , если соседи явно представлены графом, и на состязательное обучение, если соседи неявно индуцируются состязательными возмущениями.
Общий рабочий процесс нейронного структурированного обучения показан ниже. Черные стрелки представляют традиционный рабочий процесс обучения, а красные стрелки представляют новый рабочий процесс, представленный NSL для использования структурированных сигналов. Во-первых, обучающие выборки дополняются структурированными сигналами. Когда структурированные сигналы не предоставляются явно, их можно либо сконструировать, либо индуцировать (последнее применимо к состязательному обучению). Затем расширенные обучающие выборки (включая как исходные выборки, так и их соответствующих соседей) передаются в нейронную сеть для расчета их вложений. Расстояние между внедрением выборки и внедрением его соседа рассчитывается и используется как потеря соседа, которая рассматривается как член регуляризации и добавляется к окончательным потерям. Для явной регуляризации на основе соседей мы обычно вычисляем потерю соседей как расстояние между внедрением выборки и внедрением соседа. Однако для вычисления потерь соседей можно использовать любой уровень нейронной сети. С другой стороны, для индуцированной регуляризации на основе соседей (состязательной) мы вычисляем потерю соседей как расстояние между выходным предсказанием индуцированного состязательного соседа и основной истинной меткой.

Зачем использовать NSL?
NSL имеет следующие преимущества:
- Более высокая точность : структурированные сигналы среди выборок могут предоставлять информацию, которая не всегда доступна во входных данных объекта; поэтому было показано, что подход к совместному обучению (как со структурированными сигналами, так и с функциями) превосходит многие существующие методы (которые основаны на обучении только с использованием функций) для широкого круга задач, таких как классификация документов и классификация семантических намерений ( Bui et al. ., WSDM'18 и Кипф и др., ICLR'17 ).
- Устойчивость : было показано, что модели, обученные на состязательных примерах, устойчивы к состязательным возмущениям, призванным ввести в заблуждение прогноз или классификацию модели ( Goodfellow et al., ICLR'15 и Miyato et al., ICLR'16 ). Когда количество обучающих выборок невелико, обучение на состязательных примерах также помогает повысить точность модели ( Ципрас и др., ICLR'19 ).
- Требуется меньше размеченных данных : NSL позволяет нейронным сетям использовать как размеченные, так и неразмеченные данные, что расширяет парадигму обучения до полуконтролируемого обучения . В частности, NSL позволяет сети обучаться с использованием помеченных данных, как в контролируемой настройке, и в то же время заставляет сеть изучать аналогичные скрытые представления для «соседних образцов», которые могут иметь или не иметь метки. Этот метод показал большие перспективы для повышения точности модели, когда объем размеченных данных относительно невелик ( Bui et al., WSDM'18 и Miyato et al., ICLR'16 ).
Пошаговые руководства
Чтобы получить практический опыт работы с нейронным структурированным обучением, у нас есть учебные пособия, охватывающие различные сценарии, в которых структурированные сигналы могут быть явно заданы, созданы или вызваны. Вот некоторые из них:
Регуляризация графов для классификации документов с использованием естественных графов . В этом уроке мы исследуем использование регуляризации графа для классификации документов, образующих естественный (органический) граф.
Регуляризация графов для классификации настроений с использованием синтезированных графиков . В этом уроке мы демонстрируем использование регуляризации графов для классификации настроений в обзорах фильмов путем построения (синтеза) структурированных сигналов.
Состязательное обучение для классификации изображений . В этом уроке мы исследуем использование состязательного обучения (при котором индуцируются структурированные сигналы) для классификации изображений, содержащих числовые цифры.
Дополнительные примеры и руководства можно найти в каталоге примеров нашего репозитория GitHub.

