TensorFlow.orgで表示 TensorFlow.orgで表示 |
 Google Colab で実行 Google Colab で実行 |
 GitHub でソースを表示{ GitHub でソースを表示{ |
 ノートブックをダウンロード/a0} ノートブックをダウンロード/a0} |
概要
このノートブックでは、アドオンパッケージのConditional Gradientオプティマイザの使用方法を紹介します。
ConditionalGradient
根本的な正則化の効果を出すために、ニューラルネットワークのパラメーターを制約することがトレーニングに有益であることが示されています。多くの場合、パラメーターはソフトペナルティ(制約充足を保証しない)または投影操作(計算コストが高い)によって制約されますが、Conditional Gradient(CG)オプティマイザは、費用のかかる投影ステップを必要とせずに、制約を厳密に適用します。これは、制約内のオブジェクトの線形近似を最小化することによって機能します。このノートブックでは、MNISTデータセットに対してCGオプティマイザを使用してフロベニウスノルム制約を適用する方法を紹介します。CGは、tensorflow APIとして利用可能になりました。オプティマイザの詳細は、https://arxiv.org/pdf/1803.06453.pdfを参照してください。
セットアップ
pip install -q -U tensorflow-addonsimport tensorflow as tf
import tensorflow_addons as tfa
from matplotlib import pyplot as plt
# Hyperparameters
batch_size=64
epochs=10
モデルの構築
model_1 = tf.keras.Sequential([
tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])
データの準備
# Load MNIST dataset as NumPy arrays
dataset = {}
num_validation = 10000
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# Preprocess the data
x_train = x_train.reshape(-1, 784).astype('float32') / 255
x_test = x_test.reshape(-1, 784).astype('float32') / 255
カスタムコールバック関数の定義
def frobenius_norm(m):
"""This function is to calculate the frobenius norm of the matrix of all
layer's weight.
Args:
m: is a list of weights param for each layers.
"""
total_reduce_sum = 0
for i in range(len(m)):
total_reduce_sum = total_reduce_sum + tf.math.reduce_sum(m[i]**2)
norm = total_reduce_sum**0.5
return norm
CG_frobenius_norm_of_weight = []
CG_get_weight_norm = tf.keras.callbacks.LambdaCallback(
on_epoch_end=lambda batch, logs: CG_frobenius_norm_of_weight.append(
frobenius_norm(model_1.trainable_weights).numpy()))
トレーニングと評価:オプティマイザとしてCGを使用
一般的なkerasオプティマイザを新しいtfaオプティマイザに置き換えるだけです。
# Compile the model
model_1.compile(
optimizer=tfa.optimizers.ConditionalGradient(
learning_rate=0.99949, lambda_=203), # Utilize TFA optimizer
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=['accuracy'])
history_cg = model_1.fit(
x_train,
y_train,
batch_size=batch_size,
validation_data=(x_test, y_test),
epochs=epochs,
callbacks=[CG_get_weight_norm])
Epoch 1/10 938/938 [==============================] - 4s 3ms/step - loss: 0.5909 - accuracy: 0.8229 - val_loss: 0.2154 - val_accuracy: 0.9306 Epoch 2/10 938/938 [==============================] - 2s 3ms/step - loss: 0.1963 - accuracy: 0.9410 - val_loss: 0.1732 - val_accuracy: 0.9437 Epoch 3/10 938/938 [==============================] - 3s 3ms/step - loss: 0.1582 - accuracy: 0.9531 - val_loss: 0.1470 - val_accuracy: 0.9542 Epoch 4/10 938/938 [==============================] - 3s 3ms/step - loss: 0.1372 - accuracy: 0.9579 - val_loss: 0.1361 - val_accuracy: 0.9601 Epoch 5/10 938/938 [==============================] - 2s 3ms/step - loss: 0.1193 - accuracy: 0.9633 - val_loss: 0.1257 - val_accuracy: 0.9626 Epoch 6/10 938/938 [==============================] - 2s 3ms/step - loss: 0.1167 - accuracy: 0.9657 - val_loss: 0.1255 - val_accuracy: 0.9636 Epoch 7/10 938/938 [==============================] - 3s 3ms/step - loss: 0.1113 - accuracy: 0.9664 - val_loss: 0.1352 - val_accuracy: 0.9573 Epoch 8/10 938/938 [==============================] - 3s 3ms/step - loss: 0.1084 - accuracy: 0.9674 - val_loss: 0.1127 - val_accuracy: 0.9643 Epoch 9/10 938/938 [==============================] - 3s 3ms/step - loss: 0.1059 - accuracy: 0.9680 - val_loss: 0.1164 - val_accuracy: 0.9623 Epoch 10/10 938/938 [==============================] - 3s 3ms/step - loss: 0.1037 - accuracy: 0.9684 - val_loss: 0.1096 - val_accuracy: 0.9658
トレーニングと評価:オプティマイザとしてSGDを使用
model_2 = tf.keras.Sequential([
tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])
SGD_frobenius_norm_of_weight = []
SGD_get_weight_norm = tf.keras.callbacks.LambdaCallback(
on_epoch_end=lambda batch, logs: SGD_frobenius_norm_of_weight.append(
frobenius_norm(model_2.trainable_weights).numpy()))
# Compile the model
model_2.compile(
optimizer=tf.keras.optimizers.SGD(0.01), # Utilize SGD optimizer
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=['accuracy'])
history_sgd = model_2.fit(
x_train,
y_train,
batch_size=batch_size,
validation_data=(x_test, y_test),
epochs=epochs,
callbacks=[SGD_get_weight_norm])
Epoch 1/10 938/938 [==============================] - 2s 2ms/step - loss: 1.5189 - accuracy: 0.5707 - val_loss: 0.4277 - val_accuracy: 0.8873 Epoch 2/10 938/938 [==============================] - 2s 2ms/step - loss: 0.4073 - accuracy: 0.8885 - val_loss: 0.3210 - val_accuracy: 0.9091 Epoch 3/10 938/938 [==============================] - 2s 2ms/step - loss: 0.3214 - accuracy: 0.9070 - val_loss: 0.2891 - val_accuracy: 0.9154 Epoch 4/10 938/938 [==============================] - 2s 2ms/step - loss: 0.2848 - accuracy: 0.9174 - val_loss: 0.2577 - val_accuracy: 0.9251 Epoch 5/10 938/938 [==============================] - 2s 2ms/step - loss: 0.2644 - accuracy: 0.9222 - val_loss: 0.2427 - val_accuracy: 0.9293 Epoch 6/10 938/938 [==============================] - 2s 2ms/step - loss: 0.2453 - accuracy: 0.9297 - val_loss: 0.2287 - val_accuracy: 0.9346 Epoch 7/10 938/938 [==============================] - 2s 2ms/step - loss: 0.2262 - accuracy: 0.9338 - val_loss: 0.2216 - val_accuracy: 0.9365 Epoch 8/10 938/938 [==============================] - 2s 2ms/step - loss: 0.2181 - accuracy: 0.9374 - val_loss: 0.2031 - val_accuracy: 0.9405 Epoch 9/10 938/938 [==============================] - 2s 2ms/step - loss: 0.1978 - accuracy: 0.9420 - val_loss: 0.1906 - val_accuracy: 0.9452 Epoch 10/10 938/938 [==============================] - 2s 2ms/step - loss: 0.1908 - accuracy: 0.9450 - val_loss: 0.1870 - val_accuracy: 0.9459
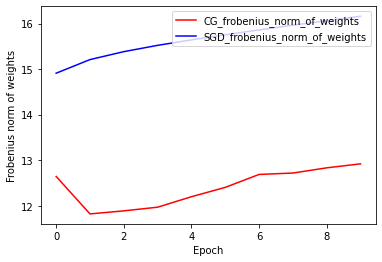
重みのフロベニウスノルム:CGとSGDの比較
現在のCGオプティマイザの実装はフロベニウスノルムに基づいており、フロベニウスノルムをターゲット関数の正則化機能と見なしています。ここでは、CGオプティマイザの正規化された効果を、フロベニウスノルム正則化機能のないSGDオプティマイザと比較します。
plt.plot(
CG_frobenius_norm_of_weight,
color='r',
label='CG_frobenius_norm_of_weights')
plt.plot(
SGD_frobenius_norm_of_weight,
color='b',
label='SGD_frobenius_norm_of_weights')
plt.xlabel('Epoch')
plt.ylabel('Frobenius norm of weights')
plt.legend(loc=1)
<matplotlib.legend.Legend at 0x7fbf3c16dc50>
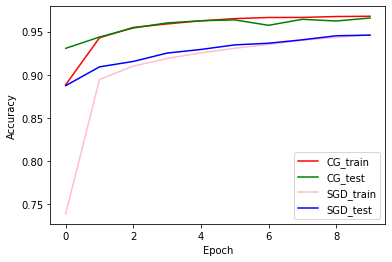
トレーニングと検証の精度:CGとSGDの比較
plt.plot(history_cg.history['accuracy'], color='r', label='CG_train')
plt.plot(history_cg.history['val_accuracy'], color='g', label='CG_test')
plt.plot(history_sgd.history['accuracy'], color='pink', label='SGD_train')
plt.plot(history_sgd.history['val_accuracy'], color='b', label='SGD_test')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(loc=4)
<matplotlib.legend.Legend at 0x7fbf3c0d1e10>