 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
pip install -q -U jax jaxlibpip install -q -Uq oryx -Ipip install -q tfp-nightly --upgrade
from functools import partial
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')
import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
import oryx
La programación probabilística es la idea de que podemos expresar modelos probabilísticos utilizando características de un lenguaje de programación. Las tareas como la inferencia bayesiana o la marginación se proporcionan como características del lenguaje y potencialmente pueden automatizarse.
Oryx proporciona un sistema de programación probabilística en el que los programas probabilísticos se expresan simplemente como funciones de Python; ¡estos programas luego se transforman a través de transformaciones de funciones componibles como las de JAX! La idea es comenzar con programas simples (como el muestreo de una normal aleatoria) y componerlos juntos para formar modelos (como una red neuronal bayesiana). Un punto importante del diseño de PPL Oryx es permitir a los programas para parecerse a las funciones que ya habías escribir y su uso en JAX, pero son anotados para hacer transformaciones consciente de ellos.
Primero importemos la funcionalidad principal de PPL de Oryx.
from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest
¿Qué son los programas probabilísticos en Oryx?
En Oryx, los programas probabilísticos son solo funciones Python puras que operan en valores JAX y claves pseudoaleatorias y devuelven una muestra aleatoria. Por su diseño, son compatibles con las transformaciones como jit y vmap . Sin embargo, el sistema de programación probabilística Oryx proporciona herramientas que le permiten anotar sus funciones de manera útil.
Siguiendo la filosofía de JAX funciones puras, un programa probabilístico Oryx es una función de Python que toma un JAX PRNGKey como primer argumento y cualquier número de argumentos posteriores acondicionado. La salida de la función se llama una "muestra" y las mismas restricciones que se aplican a jit -ed y vmap funciones -ed aplican a los programas probabilísticos (por ejemplo, no hay flujo de datos dependiente de control, no hay efectos secundarios, etc.). Esto difiere de muchos sistemas de programación probabilística imperativos en los que una "muestra" es la traza de ejecución completa, incluidos los valores internos de la ejecución del programa. Veremos más adelante cómo Oryx puede acceder a los valores internos mediante el joint_sample , se discute a continuación.
Program :: PRNGKey -> ... -> Sample
Aquí hay un programa "hola mundo" que las muestras de una distribución logarítmica normal .
def log_normal(key):
return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.) 0.8139614 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
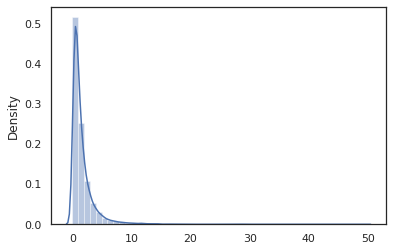
El log_normal función es una envoltura delgada alrededor de un Tensorflow Probabilidad (PTF) de distribución, pero en lugar de llamar tfd.Normal(0., 1.).sample , hemos utilizado random_variable lugar. Como veremos más adelante, random_variable nos permite convertir los objetos en los programas probabilísticos, junto con otras funciones útiles.
Podemos convertir log_normal en un diario de función de la densidad mediante el log_prob transformación:
print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()
-0.9189385
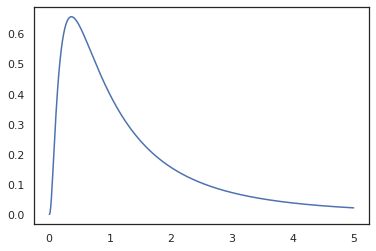
Debido a que hemos anotado la función con random_variable , log_prob es consciente de que hubo una llamada a tfd.Normal(0., 1.).sample y utiliza tfd.Normal(0., 1.).log_prob para calcular la distribución de base problema de registro Para manejar el jnp.exp , ppl.log_prob calcula automáticamente densidades a través de funciones biyectivas, hacer el seguimiento de los cambios de volumen en el cálculo de cambio de variable.
En Oryx, podemos tomar los programas y transformarlos usando transformaciones de función - por ejemplo, jax.jit o log_prob . Sin embargo, Oryx no puede hacer esto con cualquier programa; requiere funciones de muestreo que hayan registrado su función de densidad logarítmica con Oryx. Afortunadamente, Oryx registra automáticamente TensorFlow Probabilidad distribuciones (PTF) en su sistema.
Herramientas de programación probabilística de Oryx
Oryx tiene varias transformaciones de funciones orientadas a la programación probabilística. Repasaremos la mayoría de ellos y proporcionaremos algunos ejemplos. Al final, lo pondremos todo junto en un estudio de caso de MCMC. También puede hacer referencia a la documentación de core.ppl.transformations para más detalles.
random_variable
random_variable tiene dos piezas principales de funcionalidad, tanto centrado en la anotación de las funciones de Python con la información que se puede utilizar en las transformaciones.
random_variable'funciona como la función identidad por defecto, pero se puede utilizar registros específicos para tipos de objetos a convertir en programs.` probabilísticoPara los tipos exigibles (funciones de Python, lambdas,
functools.partials, etc.) y arbitrariaobjects (como JAXDeviceArrays) se acaba de regresar su entrada.random_variable(x: object) == x random_variable(f: Callable[...]) == fOryx registra automáticamente TensorFlow Probabilidad (PTF) distribuciones, que se convierten en los programas probabilísticos que la llamada de la distribución
samplemétodo.random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235Además, Oryx incorpora información sobre la distribución de TFP en trazas JAX que permite calcular automáticamente las densidades de registros.
random_variablevalores de variables lata con nombres, que los hace útiles para las transformaciones posteriores, proporcionando una opciónnameargumento de palabra clave arandom_variable. Cuando se pasa una matriz enrandom_variablejunto con unname(por ejemplorandom_variable(x, name='x')), sólo se etiqueta el valor y la devuelve. Si pasamos en una, exigible o distribución PTFrandom_variablevuelve un programa que muestra las etiquetas de su salida conname.
Estas anotaciones no cambian la semántica del programa cuando se ejecuta, pero sólo cuando transformada (es decir, el programa volverá el mismo valor con o sin el uso de random_variable ).
Repasemos un ejemplo en el que usamos ambas funciones juntas.
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
En este programa se ha etiquetado los compuestos intermedios z y x , lo que hace que el transformaciones joint_sample , intervene , conditional y graph_replace conscientes de los nombres 'z' y 'x' . Repasaremos exactamente cómo cada transformación usa nombres más adelante.
log_prob
El log_prob transformación función convierte un programa probabilístico Oryx en su función de registro de densidad. Esta función de densidad logarítmica toma una muestra potencial del programa como entrada y devuelve su densidad logarítmica bajo la distribución de muestreo subyacente.
log_prob :: Program -> (Sample -> LogDensity)
Al igual que random_variable , funciona a través de un registro de los tipos donde las distribuciones de la PTF se registran automáticamente, por lo log_prob(tfd.Normal(0., 1.)) llama tfd.Normal(0., 1.).log_prob . Para las funciones de Python, sin embargo, log_prob traza el programa utilizando JAX y miradas para el muestreo de las declaraciones. El log_prob transformación funciona en la mayoría de los programas que devuelven variables aleatorias, directamente oa través de transformaciones invertibles, pero no en los programas que internamente valores de muestra que no se devuelven. Si no se puede invertir las operaciones necesarias en el programa, log_prob generará un error.
Estos son algunos ejemplos de log_prob aplicadas a diversos programas.
-
log_probtrabaja en programas que directamente de la muestra a partir de distribuciones de la PTF (u otros tipos registrados) y devolver sus valores.
def normal(key):
return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))
-0.9189385
-
log_probes capaz de calcular log-densidades de las muestras de los programas que transforman variables aleatorias aleatorios usando funciones biyectivas (por ejemplojnp.exp,jnp.tanh,jnp.split).
def log_normal(key):
return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))
-1.159165
Con el fin de calcular una muestra de log_normal 's registro de densidad, en primer lugar hay que invertir la exp , teniendo el log de la muestra, y luego añadir una corrección del volumen de cambio mediante el registro en Calle jacobiano inverso de exp (ver el cambio de la variable fórmula de Wikipedia).
-
log_probtrabaja con programas que las estructuras de producción de las muestras gusta, diccionarios de Python o tuplas.
def normal_2d(key):
x = random_variable(
tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
x1, x2 = jnp.split(x, 2, 0)
return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))
{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546
-
log_probcamina el gráfico de cálculo trazado de la función, el cálculo de ambos valores directa e inversa (y su log-det jacobianos) cuando sea necesario, en un intento para conectar valores devueltos con sus valores muestreados base a través de un cambio bien definido de variables. Tome el siguiente programa de ejemplo:
def complex_program(key):
k1, k2 = random.split(key)
z = random_variable(tfd.Normal(0., 1.))(k1)
x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))
(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32)) -1.0967848
En este programa, se muestra x condicionalmente en z , lo que significa que necesitan el valor de z antes de que podamos calcular el registro de densidad de x . Sin embargo, con el fin de calcular z , primero tenemos que invertir la jnp.exp aplica a z . Por lo tanto, con el fin de calcular el log-densidades de x y z , log_prob necesidades a primera invertido la primera salida, y luego pasarla hacia adelante a través de la jax.nn.relu para calcular la media de p(x | z) .
Para obtener más información acerca de log_prob , puede hacer referencia a core.interpreters.log_prob . En la aplicación, log_prob se basa estrechamente fuera de la inverse la transformación JAX; para aprender más acerca inverse , ver core.interpreters.inverse .
joint_sample
Para definir programas más complejos e interesantes, usaremos algunas variables aleatorias latentes, es decir, variables aleatorias con valores no observados. Vamos a referirnos a la latent_normal programa que las muestras de un valor aleatorio z que se utiliza como la media de otro valor aleatorio x .
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
En este programa, z es tan latente si tuviéramos que acaba de llamar latent_normal(random.PRNGKey(0)) no conoceríamos el valor real de z que es responsable de la generación x .
joint_sample es una transformación que transforma un programa en otro programa que devuelve un diccionario nombres de cadena de mapeo (tags) a sus valores. Para que funcione, debemos asegurarnos de etiquetar las variables latentes para asegurarnos de que aparezcan en la salida de la función transformada.
joint_sample(latent_normal)(random.PRNGKey(0))
{'x': DeviceArray(0.01873656, dtype=float32),
'z': DeviceArray(0.14389044, dtype=float32)}
Tenga en cuenta que joint_sample transforma un programa en otro programa que las muestras de la distribución conjunta sobre sus valores latentes, por lo que pueden transformar aún más. Para algoritmos como MCMC y VI, es común calcular la probabilidad logarítmica de la distribución conjunta como parte del procedimiento de inferencia. log_prob(latent_normal) no funciona, ya que requiere marginar a cabo z , pero podemos utilizar log_prob(joint_sample(latent_normal)) .
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))
-50.03529 -5049.535
Debido a que este es un patrón tan común, Oryx también tiene un joint_log_prob transformación que es sólo la composición de log_prob y joint_sample .
print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))
-50.03529 -5049.535
block
El block transformación se lleva en un programa y una secuencia de nombres y devuelve un programa que se comporta de forma idéntica, excepto que en transformaciones posteriores (como joint_sample ), los nombres proporcionados son ignorados. Un ejemplo de donde block es útil es la conversión de una distribución conjunta en una previa sobre las variables latentes por "bloqueo" los valores muestreados en la probabilidad. Por ejemplo, tome latent_normal , que primero dibuja una z ~ N(0, 1) a continuación, un x | z ~ N(z, 1e-1) . block(latent_normal, names=['x']) es un programa que oculta la x nombre, por lo que si hacemos joint_sample(block(latent_normal, names=['x'])) , obtenemos un diccionario con sólo z en ella .
blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))
{'z': DeviceArray(0.14389044, dtype=float32)}
intervene
La intervene muestras clobbers transformación en un programa probabilístico con los valores del exterior. Volviendo a nuestro latent_normal programa, digamos que estábamos interesados en ejecutar el mismo programa pero quería z para fijarse a 4. En lugar de escribir un nuevo programa, podemos utilizar intervene para alterar temporalmente el valor de z .
intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
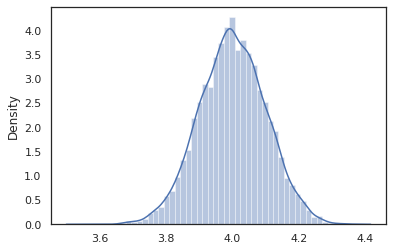
Los intervened muestras de función de p(x | do(z = 4)) que es sólo una distribución normal estándar centrada a 4. Cuando intervene en un valor particular, que el valor ya no se considera una variable aleatoria. Esto significa que una z valor no se etiquetarán durante la ejecución intervened .
conditional
conditional transformadas de un programa que muestras latentes valores en uno que las condiciones en esos valores latentes. Volviendo a nuestro latent_normal programa, que las muestras p(x) con una latente z , podemos convertirlo en un programa condicional p(x | z) .
cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()
99.87485 49.874847 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning) /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)

nest
Cuando comenzamos a componer programas probabilísticos para construir programas más complejos, es común reutilizar funciones que tienen una lógica importante. Por ejemplo, si nos gustaría construir una red neuronal bayesiana, podría ser un importante dense programa que muestras de pesos y se ejecuta un pase hacia adelante.
Si reutilizamos funciones, sin embargo, podríamos terminar con valores etiquetados duplicadas en el programa final, que se anuló por transformaciones como joint_sample . Podemos usar el nest para crear la etiqueta "Miras" en el que se insertan las muestras dentro de un ámbito con nombre en un diccionario anidada.
def f(key):
return random_variable(tfd.Normal(0., 1.), name='x')(key)
def g(key):
k1, k2 = random.split(key)
return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))
{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }
Estudio de caso: red neuronal bayesiana
Vamos a probar nuestra mano en la formación de una red neuronal bayesiano para clasificar el clásico Fisher Iris conjunto de datos. Es relativamente pequeño y de pocas dimensiones, por lo que podemos intentar muestrear directamente la parte posterior con MCMC.
Primero, importemos el conjunto de datos y algunas utilidades adicionales de Oryx.
from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
from oryx.experimental import mcmc
from oryx.util import summary, get_summaries
Comenzamos implementando una capa densa, que tendrá a priori normales sobre los pesos y el sesgo. Para ello, en primer lugar definir una dense función de orden superior que se lleva en la función de la dimensión de salida y la activación deseada. La dense función devuelve un programa probabilístico que representa una distribución condicional p(h | x) , donde h es la salida de una capa densa y x es su entrada. It primeras muestras el peso y sesgo y luego las aplica a x .
def dense(dim_out, activation=jax.nn.relu):
def forward(key, x):
dim_in = x.shape[-1]
w_key, b_key = random.split(key)
w = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
name='w')(w_key)
b = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
name='b')(b_key)
return activation(jnp.dot(w, x) + b)
return forward
Para componer varias dense capas juntas, vamos a implementar un mlp más alta función de orden (perceptrón multicapa) que toma en una lista de tamaños ocultos y una serie de clases. Devuelve un programa que llama repetidamente dense utilizando la apropiada hidden_size y finalmente devuelve logit para cada clase en la capa final. Observe el uso de nest que crea ámbitos de nombre para cada capa.
def mlp(hidden_sizes, num_classes):
num_hidden = len(hidden_sizes)
def forward(key, x):
keys = random.split(key, num_hidden + 1)
for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
logits = nest(dense(num_classes, activation=lambda x: x),
scope=f'layer_{num_hidden + 1}')(keys[-1], x)
return logits
return forward
Para implementar el modelo completo, necesitaremos modelar las etiquetas como variables aleatorias categóricas. Vamos a definir un predict función que toma en un conjunto de datos de xs (las características) que luego se pasan en un mlp usando vmap . Cuando usamos vmap(partial(mlp, mlp_key)) , nos muestra un único conjunto de pesos, pero en el mapa los pase hacia adelante sobre toda la entrada xs . Esto produce un conjunto de logits la que parametriza distribuciones categóricas independientes.
def predict(mlp):
def forward(key, xs):
mlp_key, label_key = random.split(key)
logits = vmap(partial(mlp, mlp_key))(xs)
return random_variable(
tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
return forward
¡Ese es el modelo completo! Usemos MCMC para muestrear la parte posterior de las ponderaciones BNN dadas los datos; primero se construye un BNN "plantilla" utilizando mlp .
bnn = mlp([200, 200], num_classes)
Para construir un punto de partida para nuestra cadena de Markov, podemos utilizar joint_sample con una entrada de maniquí.
weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())
dict_keys(['layer_1', 'layer_2', 'layer_3'])
Calcular la probabilidad logarítmica de la distribución conjunta es suficiente para muchos algoritmos de inferencia. Ahora vamos a decir que observamos x y queremos probar la posterior p(z | x) . Para distribuciones complejas, no vamos a ser capaces de marginar a cabo x (aunque para latent_normal podemos) pero podemos calcular una densidad de registro unnormalized log p(z, x) donde x se fija a un valor particular. Podemos usar la probabilidad logarítmica no normalizada con MCMC para muestrear el posterior. Escribamos esta función de problema de registro "anclado".
def target_log_prob(weights):
return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)
Ahora podemos usar tfp.mcmc para probar la posterior utilizando nuestra función de densidad de registro no normalizada. Tenga en cuenta que vamos a tener que utilizar un "aplanado" versión de nuestros pesos anidados diccionario para ser compatible con tfp.mcmc , por lo que utilizar los servicios públicos de árboles de Jax para aplanar y unflatten.
@jit
def run_chain(key, weights):
flat_state, sample_tree = jax.tree_flatten(weights)
def flat_log_prob(*states):
return target_log_prob(jax.tree_unflatten(sample_tree, states))
def trace_fn(_, results):
return results.inner_results.accepted_results.target_log_prob
flat_states, log_probs = tfp.mcmc.sample_chain(
1000,
num_burnin_steps=9000,
kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
9000, target_accept_prob=0.7),
trace_fn=trace_fn,
current_state=flat_state,
seed=key)
samples = jax.tree_unflatten(sample_tree, flat_states)
return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)
plt.plot(log_probs)
plt.show()
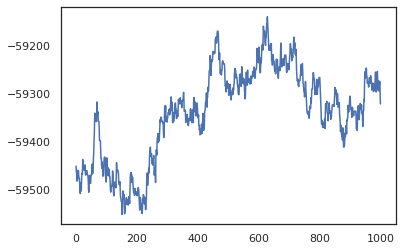
Podemos usar nuestras muestras para tomar una estimación de promedio de modelo bayesiano (BMA) de la precisión del entrenamiento. Para calcularla, podemos utilizar intervene con bnn "inyectar" posterior pesos en lugar de los que son la muestra de la llave. Para calcular logit para cada punto de datos para cada muestra posterior, podemos doblar vmap sobre posterior_weights y features .
output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)
print('Average sample accuracy:', (
output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())
Average sample accuracy: 0.9874067 BMA accuracy: 0.99333334
Conclusión
En Oryx, los programas probabilísticos son solo funciones JAX que toman en (pseudo) aleatoriedad como entrada. Debido a la estrecha integración de Oryx con el sistema de transformación de funciones de JAX, podemos escribir y manipular programas probabilísticos como si estuviéramos escribiendo código JAX. Esto da como resultado un sistema simple pero flexible para construir modelos complejos y hacer inferencias.
