 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
pip install -q -U jax jaxlibpip install -q -Uq oryx -Ipip install -q tfp-nightly --upgrade
from functools import partial
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')
import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
import oryx
Programação probabilística é a ideia de que podemos expressar modelos probabilísticos usando recursos de uma linguagem de programação. Tarefas como inferência bayesiana ou marginalização são fornecidas como recursos de linguagem e podem ser automatizadas.
Oryx fornece um sistema de programação probabilística no qual programas probabilísticos são expressos apenas como funções Python; esses programas são então transformados por meio de transformações de função combináveis, como aquelas em JAX! A ideia é começar com programas simples (como amostragem de um normal aleatório) e compô-los juntos para formar modelos (como uma rede neural bayesiana). Um ponto importante do projeto PPL do Oryx é permitir que os programas para se parecer com funções que você já ia escrever e uso de JAX, mas são anotados para fazer transformações conscientes deles.
Vamos primeiro importar a funcionalidade PPL central do Oryx.
from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest
O que são programas probabilísticos no Oryx?
No Oryx, os programas probabilísticos são apenas funções Python puras que operam em valores JAX e chaves pseudo-aleatórias e retornam uma amostra aleatória. Pelo projeto, eles são compatíveis com as transformações como jit e vmap . No entanto, o sistema de programação probabilística Oryx fornece ferramentas que permitem a você anotar suas funções de maneira útil.
Seguindo a filosofia JAX de funções puras, um programa probabilística Oryx é uma função Python que leva um JAX PRNGKey como seu primeiro argumento e qualquer número de argumentos condicionado subseqüentes. A saída da função é chamada uma "amostra" e as mesmas restrições que se aplicam a jit -ed e vmap funções -ED aplicar a programas de probabilidade (por exemplo, nenhum fluxo de dados dependente de controlo, não há efeitos secundários, etc.). Isso difere de muitos sistemas de programação probabilísticos imperativos em que uma 'amostra' é o rastreamento de execução inteiro, incluindo valores internos para a execução do programa. Veremos mais tarde como Oryx pode acessar valores internos usando o joint_sample , discutido abaixo.
Program :: PRNGKey -> ... -> Sample
Aqui está um programa "Olá mundo" que as amostras de uma distribuição log-normal .
def log_normal(key):
return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.) 0.8139614 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
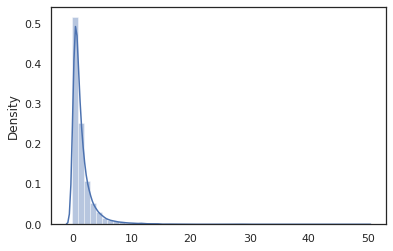
O log_normal função é um wrapper fino em torno de um Tensorflow Probabilidade (TFP) de distribuição, mas em vez de chamar tfd.Normal(0., 1.).sample , nós usamos random_variable vez. Como veremos mais tarde, random_variable nos permite converter objetos em programas probabilísticos, juntamente com outras funcionalidades úteis.
Podemos converter log_normal em uma função de log-densidade usando o log_prob transformação:
print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()
-0.9189385
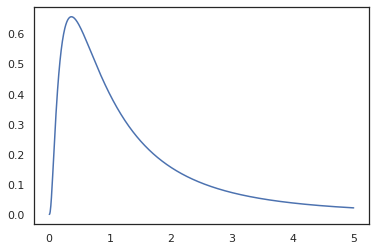
Porque nós temos anotado a função com random_variable , log_prob está ciente de que havia uma chamada para tfd.Normal(0., 1.).sample e usa tfd.Normal(0., 1.).log_prob para calcular a distribuição base log prob. Para lidar com a jnp.exp , ppl.log_prob calcula automaticamente densidades através de funções bijective, mantendo o controle de mudanças de volume no cálculo de mudança de variável.
Em Oryx, podemos tomar programas e transformá-los usando transformações de função - por exemplo, jax.jit ou log_prob . Oryx não pode fazer isso com qualquer programa; requer funções de amostragem que tenham registrado sua função de densidade de registro com Oryx. Felizmente, Oryx registra automaticamente TensorFlow Probabilidade distribuições (TFP) em seu sistema.
Ferramentas de programação probabilística do Oryx
Oryx tem várias transformações de função voltadas para a programação probabilística. Examinaremos a maioria deles e forneceremos alguns exemplos. No final, colocaremos tudo junto em um estudo de caso MCMC. Você também pode consultar a documentação para core.ppl.transformations para mais detalhes.
random_variable
random_variable tem duas principais peças de funcionalidade, ambos focados em anotar as funções do Python com informações que podem ser usadas em transformações.
random_variable'opera como a função identidade por padrão, mas pode usar registros de tipo específico de objetos converter em programs.` probabilísticaPara tipos que podem ser chamados (as funções do Python, lambdas,
functools.partials, etc.) e arbitrárioobjects (como JAXDeviceArrays) ele só vai voltar sua entrada.random_variable(x: object) == x random_variable(f: Callable[...]) == fOryx regista automaticamente TensorFlow Probabilidade (TFP) distribuições, que são convertidos em programas probabilística que chamam a de distribuição de
samplemétodo.random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235O Oryx adicionalmente incorpora informações sobre a distribuição TFP em rastreamentos JAX que permitem a computação automática de densidades de log.
random_variablevalores pode marcar com nomes, tornando-os úteis para transformações jusante, fornecendo um opcionalnameargumento palavra-chave pararandom_variable. Quando se passar uma matriz emrandom_variablejuntamente com umname(por exemplo,random_variable(x, name='x')), que apenas é marcado para o valor e devolve-lo. Se passar em um exigível ou distribuição TFP,random_variableretorna um programa que tags de sua amostra de saída comname.
Essas anotações não alterar a semântica do programa quando executado, mas só quando transformada (ou seja, o programa irá devolver o mesmo valor com ou sem o uso de random_variable ).
Vamos examinar um exemplo em que usamos as duas partes da funcionalidade juntas.
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
Neste programa temos marcado a intermediários z e x , o que torna a transformações joint_sample , intervene , conditional e graph_replace ciente dos nomes 'z' e 'x' . Veremos exatamente como cada transformação usa nomes posteriormente.
log_prob
O log_prob transformação de função converte um programa probabilística Oryx para a sua função de log-densidade. Esta função de densidade de log pega uma amostra potencial do programa como entrada e retorna sua densidade de log sob a distribuição de amostragem subjacente.
log_prob :: Program -> (Sample -> LogDensity)
Como random_variable , ele funciona através de um registo de tipos de onde distribuições TFP são automaticamente registradas, de modo log_prob(tfd.Normal(0., 1.)) chama tfd.Normal(0., 1.).log_prob . Para as funções do Python, no entanto, log_prob traça o programa usando JAX e olha para a amostragem declarações. O log_prob transformação funciona na maioria dos programas que retornam variáveis aleatórias, directamente ou através de transformações inversíveis mas não em programas que valores de amostra internamente que não são devolvidos. Se ele não pode inverter as operações necessárias no programa, log_prob irá lançar um erro.
Aqui estão alguns exemplos de log_prob aplicadas a vários programas.
-
log_probfunciona em programas que diretamente amostra de distribuições TFP (ou outros tipos registrados) e retornam seus valores.
def normal(key):
return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))
-0.9189385
-
log_probé capaz de calcular log-densidades das amostras de programas que transformam variates aleatórios utilizando funções bijective (por exemplojnp.exp,jnp.tanh,jnp.split).
def log_normal(key):
return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))
-1.159165
Para calcular uma amostra de log_normal 's log-densidade, primeiro precisamos inverter a exp , tomando o log da amostra, e depois adicionar uma correção volume-mudança usando o log-det inversa Jacobian de exp (ver a mudança de variável fórmula de Wikipedia).
-
log_probobras com programas que as estruturas de amostras de saída gosta, dicionários Python ou tuplas.
def normal_2d(key):
x = random_variable(
tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
x1, x2 = jnp.split(x, 2, 0)
return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))
{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546
-
log_probcaminha o gráfico traçado cálculo da função, computação ambos os valores para a frente e inversos (e o seu log-det Jacobianos), quando necessário, numa tentativa de ligar valores devolvidos com os seus valores de amostra de base através de uma mudança bem definido de variáveis. Veja o seguinte programa de exemplo:
def complex_program(key):
k1, k2 = random.split(key)
z = random_variable(tfd.Normal(0., 1.))(k1)
x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))
(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32)) -1.0967848
Neste programa, nós amostra x condicionalmente sobre z , ou seja, nós precisamos o valor de z antes de podermos calcular o log-densidade de x . No entanto, a fim de calcular z , primeiro temos que inverta a jnp.exp aplicada a z . Assim, a fim de calcular os log-densidades de x e z , log_prob necessidades a primeira invertido a primeira saída, e depois passá-lo para a frente através do jax.nn.relu para calcular a média de p(x | z) .
Para mais informações sobre log_prob , você pode se referir a core.interpreters.log_prob . Na execução, log_prob está intimamente baseado fora do inverse transformação JAX; para saber mais sobre inverse , consulte core.interpreters.inverse .
joint_sample
Para definir programas mais complexos e interessantes, usaremos algumas variáveis aleatórias latentes, ou seja, variáveis aleatórias com valores não observados. Vamos referem-se a latent_normal programa que as amostras de um valor aleatório z que é usado como a média de um outro valor aleatório x .
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
Neste programa, z é tão latente, se fôssemos apenas chamar latent_normal(random.PRNGKey(0)) não saberíamos o valor real de z que é responsável pela geração x .
joint_sample é uma transformação que transforma um programa para outro programa que retorna um dicionário nomes cadeia de mapeamento (tags) para seus valores. Para funcionar, precisamos ter certeza de marcar as variáveis latentes para garantir que elas apareçam na saída da função transformada.
joint_sample(latent_normal)(random.PRNGKey(0))
{'x': DeviceArray(0.01873656, dtype=float32),
'z': DeviceArray(0.14389044, dtype=float32)}
Note-se que joint_sample transforma um programa para outro programa que as amostras a distribuição conjunta sobre os seus valores latentes, para que possamos transformar-la ainda mais. Para algoritmos como MCMC e VI, é comum calcular a probabilidade de log da distribuição conjunta como parte do procedimento de inferência. log_prob(latent_normal) não funciona porque requer marginalizando a z , mas podemos usar log_prob(joint_sample(latent_normal)) .
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))
-50.03529 -5049.535
Uma vez que este é um teste padrão comum tal, Oryx também tem um joint_log_prob transformação que é apenas a composição de log_prob e joint_sample .
print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))
-50.03529 -5049.535
block
O block transformação se em um programa e uma sequência de nomes e retorna um programa que se comporta de forma idêntica, excepto que em transformações a jusante (como joint_sample ), os nomes fornecidos são ignorados. Um exemplo de onde block é útil é a conversão de um conjunto de distribuição para uma prévia sobre as variáveis latentes por "bloqueio" os valores amostrados na probabilidade. Por exemplo, tomar latent_normal , que em primeiro lugar chama a um z ~ N(0, 1) , em seguida, um x | z ~ N(z, 1e-1) . block(latent_normal, names=['x']) é um programa que esconde o x nome, então se fizermos joint_sample(block(latent_normal, names=['x'])) , obtemos um dicionário com apenas z nele .
blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))
{'z': DeviceArray(0.14389044, dtype=float32)}
intervene
O intervene amostras clobbers transformação em um programa probabilística com valores a partir do exterior. Voltando ao nosso latent_normal programa, vamos dizer que estavam interessados em executar o mesmo programa, mas queria z a fixar a 4. Ao invés de escrever um novo programa, podemos usar intervene para substituir o valor de z .
intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
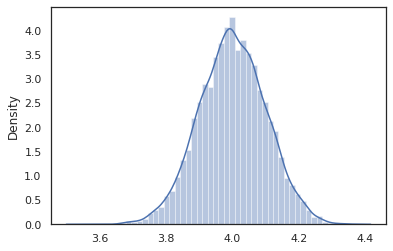
Os intervened amostras de função de p(x | do(z = 4)) , que é apenas uma distribuição normal padrão centrado em 4. Quando intervene em um determinado valor, que o valor já não é considerada uma variável aleatória. Isto significa que uma z valor não vai ser marcadas durante a execução de intervened .
conditional
conditional transforma um programa que amostras latente valores em que condições sobre esses valores latentes. Voltando ao nosso latent_normal programa, que amostras p(x) com uma latente z , podemos convertê-lo em um programa condicional p(x | z) .
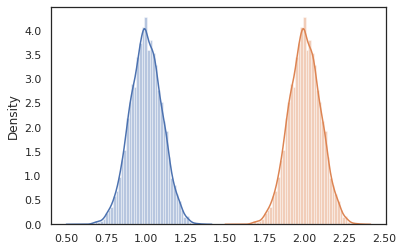
cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()
99.87485 49.874847 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning) /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
nest
Quando começamos a compor programas probabilísticos para construir outros mais complexos, é comum reutilizar funções que possuem alguma lógica importante. Por exemplo, se nós gostaríamos de construir uma rede neural Bayesian, pode haver um importante dense programa que amostras pesos e executa um passe para frente.
Se reutilizar funções, no entanto, pode acabar com os valores marcados duplicados no programa final, que é rejeitado por transformações como joint_sample . Podemos usar o nest para criar tag "escopos", onde todas as amostras dentro de um escopo nomeado será inserido em um dicionário aninhado.
def f(key):
return random_variable(tfd.Normal(0., 1.), name='x')(key)
def g(key):
k1, k2 = random.split(key)
return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))
{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }
Estudo de caso: rede neural bayesiana
Vamos tentar a nossa mão de treinamento de uma rede neural Bayesian para classificar o clássico Fisher Iris conjunto de dados. É relativamente pequeno e de baixa dimensão, então podemos tentar amostrar diretamente a parte posterior com MCMC.
Primeiro, vamos importar o conjunto de dados e alguns utilitários adicionais do Oryx.
from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
from oryx.experimental import mcmc
from oryx.util import summary, get_summaries
Começamos implementando uma camada densa, que terá antecedentes normais sobre os pesos e o viés. Para fazer isso, em primeiro lugar definir uma dense função de ordem superior que leva na função de dimensão e de saída de activação desejada. O dense função retorna um programa probabilística que representa uma distribuição condicional p(h | x) , onde h é a saída de uma camada densa e x é a sua entrada. It primeiras amostras do peso e de polarização e, em seguida, aplica-se-lhes a x .
def dense(dim_out, activation=jax.nn.relu):
def forward(key, x):
dim_in = x.shape[-1]
w_key, b_key = random.split(key)
w = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
name='w')(w_key)
b = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
name='b')(b_key)
return activation(jnp.dot(w, x) + b)
return forward
Para compor vários dense camadas juntos, vamos implementar um mlp (perceptron multicamadas) função de ordem superior que o leva em uma lista de tamanhos escondidas e um número de classes. Ele retorna um programa que repetidamente chama dense usando o apropriado hidden_size e finalmente retorna logits para cada classe na camada final. Note-se a utilização de nest que cria âmbitos nome para cada camada.
def mlp(hidden_sizes, num_classes):
num_hidden = len(hidden_sizes)
def forward(key, x):
keys = random.split(key, num_hidden + 1)
for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
logits = nest(dense(num_classes, activation=lambda x: x),
scope=f'layer_{num_hidden + 1}')(keys[-1], x)
return logits
return forward
Para implementar o modelo completo, precisaremos modelar os rótulos como variáveis aleatórias categóricas. Vamos definir uma predict função que leva em um conjunto de dados de xs (os recursos) que são então passadas para um mlp utilizando vmap . Quando usamos vmap(partial(mlp, mlp_key)) , que amostra um único conjunto de pesos, mas mapear a passagem para a frente sobre toda a entrada de xs . Isto produz um conjunto de logits que parametriza distribuições categóricas independentes.
def predict(mlp):
def forward(key, xs):
mlp_key, label_key = random.split(key)
logits = vmap(partial(mlp, mlp_key))(xs)
return random_variable(
tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
return forward
Esse é o modelo completo! Vamos usar MCMC para amostrar a posteriori dos pesos BNN dados dados; Primeiro, construir uma BNN "template" usando mlp .
bnn = mlp([200, 200], num_classes)
Para construir um ponto de partida para a cadeia de Markov, podemos usar joint_sample com uma entrada de manequim.
weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())
dict_keys(['layer_1', 'layer_2', 'layer_3'])
O cálculo da probabilidade do log de distribuição conjunta é suficiente para muitos algoritmos de inferência. Vamos agora dizer que observamos x e quer provar a posterior p(z | x) . Para distribuições complexas, não será capaz de marginalizar fora x (embora para latent_normal podemos), mas podemos calcular uma densidade unnormalized registo log p(z, x) em que x é fixado para um valor particular. Podemos usar a probabilidade de log não normalizada com MCMC para amostrar a posterior. Vamos escrever esta função de log prob "fixada".
def target_log_prob(weights):
return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)
Agora podemos usar tfp.mcmc para provar a posterior usando a nossa função densidade log unnormalized. Note que nós vamos ter que usar uma versão "achatada" dos nossos pesos aninhados dicionário para ser compatível com tfp.mcmc , por isso usamos utilitários árvores de JAX para achatar e unflatten.
@jit
def run_chain(key, weights):
flat_state, sample_tree = jax.tree_flatten(weights)
def flat_log_prob(*states):
return target_log_prob(jax.tree_unflatten(sample_tree, states))
def trace_fn(_, results):
return results.inner_results.accepted_results.target_log_prob
flat_states, log_probs = tfp.mcmc.sample_chain(
1000,
num_burnin_steps=9000,
kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
9000, target_accept_prob=0.7),
trace_fn=trace_fn,
current_state=flat_state,
seed=key)
samples = jax.tree_unflatten(sample_tree, flat_states)
return samples, log_probs
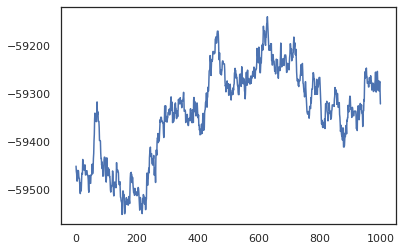
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)
plt.plot(log_probs)
plt.show()
Podemos usar nossas amostras para obter uma estimativa de média do modelo bayesiano (BMA) da precisão do treinamento. Para calculá-lo, podemos usar intervene com bnn "inserir" posterior pesos no lugar dos que são amostrados a partir da chave. Para calcular logits para cada ponto de dados para cada amostra posterior, podemos dobrar vmap sobre posterior_weights e features .
output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)
print('Average sample accuracy:', (
output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())
Average sample accuracy: 0.9874067 BMA accuracy: 0.99333334
Conclusão
No Oryx, os programas probabilísticos são apenas funções JAX que recebem (pseudo-) aleatoriedade como uma entrada. Por causa da forte integração do Oryx com o sistema de transformação de função JAX, podemos escrever e manipular programas probabilísticos como se estivéssemos escrevendo o código JAX. Isso resulta em um sistema simples, mas flexível para construir modelos complexos e fazer inferências.
