 مشاهده در TensorFlow.org مشاهده در TensorFlow.org |  در Google Colab اجرا شود در Google Colab اجرا شود |  مشاهده منبع در GitHub مشاهده منبع در GitHub |  دانلود دفترچه یادداشت دانلود دفترچه یادداشت |
این آموزش نشان می دهد که چگونه یک شبکه عصبی کلاسیک می تواند تصحیح خطاهای کالیبراسیون کیوبیت را یاد بگیرد. Cirq ، یک چارچوب پایتون را برای ایجاد، ویرایش، و فراخوانی مدارهای کوانتومی مقیاس متوسط نویزدار (NISQ) معرفی میکند و نشان میدهد که چگونه Cirq با TensorFlow کوانتومی ارتباط برقرار میکند.
برپایی
pip install tensorflow==2.7.0
TensorFlow Quantum را نصب کنید:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
اکنون TensorFlow و وابستگی های ماژول را وارد کنید:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:27:31.677071: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. مبانی
1.1 Cirq و مدارهای کوانتومی پارامتر شده
قبل از بررسی TensorFlow Quantum (TFQ)، اجازه دهید به برخی از اصول اولیه Cirq نگاه کنیم. Cirq یک کتابخانه پایتون برای محاسبات کوانتومی از گوگل است. شما از آن برای تعریف مدارها از جمله گیت های استاتیک و پارامتری استفاده می کنید.
Cirq از نمادهای SymPy برای نمایش پارامترهای رایگان استفاده می کند.
a, b = sympy.symbols('a b')
کد زیر با استفاده از پارامترهای شما یک مدار دو کیوبیتی ایجاد می کند:
# Create two qubits
q0, q1 = cirq.GridQubit.rect(1, 2)
# Create a circuit on these qubits using the parameters you created above.
circuit = cirq.Circuit(
cirq.rx(a).on(q0),
cirq.ry(b).on(q1), cirq.CNOT(control=q0, target=q1))
SVGCircuit(circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
برای ارزیابی مدارها می توانید از رابط cirq.Simulator استفاده کنید. شما با ارسال یک شی cirq.ParamResolver ، پارامترهای آزاد را در یک مدار با اعداد خاص جایگزین می کنید. کد زیر خروجی بردار حالت خام مدار پارامتری شده شما را محاسبه می کند:
# Calculate a state vector with a=0.5 and b=-0.5.
resolver = cirq.ParamResolver({a: 0.5, b: -0.5})
output_state_vector = cirq.Simulator().simulate(circuit, resolver).final_state_vector
output_state_vector
array([ 0.9387913 +0.j , -0.23971277+0.j ,
0. +0.06120872j, 0. -0.23971277j], dtype=complex64)
بردارهای حالت مستقیماً خارج از شبیه سازی قابل دسترسی نیستند (به اعداد مختلط در خروجی بالا توجه کنید). برای واقعی بودن فیزیکی، باید اندازهگیری را مشخص کنید که بردار حالت را به یک عدد واقعی تبدیل میکند که رایانههای کلاسیک بتوانند آن را درک کنند. Cirq با استفاده از ترکیبی از عملگرهای Pauli \(\hat{X}\)، \(\hat{Y}\)و \(\hat{Z}\)اندازه گیری ها را مشخص می کند. به عنوان مثال، کد زیر \(\hat{Z}_0\) و \(\frac{1}{2}\hat{Z}_0 + \hat{X}_1\) را در بردار حالتی که شما شبیه سازی کرده اید اندازه گیری می کند:
z0 = cirq.Z(q0)
qubit_map={q0: 0, q1: 1}
z0.expectation_from_state_vector(output_state_vector, qubit_map).real
0.8775825500488281
z0x1 = 0.5 * z0 + cirq.X(q1)
z0x1.expectation_from_state_vector(output_state_vector, qubit_map).real
-0.04063427448272705
1.2 مدارهای کوانتومی به عنوان تانسور
TensorFlow Quantum (TFQ) tfq.convert_to_tensor را ارائه می دهد، تابعی که اشیاء Cirq را به تانسور تبدیل می کند. این به شما امکان می دهد اشیاء Cirq را به لایه های کوانتومی و عملیات کوانتومی خود بفرستید. تابع را می توان در لیست ها یا آرایه های Cirq Circuits و Cirq Paulis فراخوانی کرد:
# Rank 1 tensor containing 1 circuit.
circuit_tensor = tfq.convert_to_tensor([circuit])
print(circuit_tensor.shape)
print(circuit_tensor.dtype)
(1,) <dtype: 'string'>
این اشیاء Cirq را به عنوان تانسور tf.string رمزگذاری می کند که عملیات tfq در صورت نیاز رمزگشایی می کند.
# Rank 1 tensor containing 2 Pauli operators.
pauli_tensor = tfq.convert_to_tensor([z0, z0x1])
pauli_tensor.shape
TensorShape([2])
1.3 شبیه سازی مدار دسته ای
TFQ روش هایی را برای محاسبه مقادیر انتظاری، نمونه ها و بردارهای حالت ارائه می دهد. در حال حاضر، بیایید بر روی مقادیر انتظارات تمرکز کنیم.
واسط بالاترین سطح برای محاسبه مقادیر انتظار، لایه tfq.layers.Expectation است که یک tf.keras.Layer است. در ساده ترین شکل خود، این لایه معادل شبیه سازی یک مدار پارامتری شده روی بسیاری از cirq.ParamResolvers . با این حال، TFQ اجازه می دهد تا دسته بندی زیر معنایی TensorFlow، و مدارها با استفاده از کد C ++ کارآمد شبیه سازی شده است.
دسته ای از مقادیر را برای جایگزینی پارامترهای a و b ایجاد کنید:
batch_vals = np.array(np.random.uniform(0, 2 * np.pi, (5, 2)), dtype=np.float32)
اجرای مدار دسته ای بر روی مقادیر پارامتر در Cirq به یک حلقه نیاز دارد:
cirq_results = []
cirq_simulator = cirq.Simulator()
for vals in batch_vals:
resolver = cirq.ParamResolver({a: vals[0], b: vals[1]})
final_state_vector = cirq_simulator.simulate(circuit, resolver).final_state_vector
cirq_results.append(
[z0.expectation_from_state_vector(final_state_vector, {
q0: 0,
q1: 1
}).real])
print('cirq batch results: \n {}'.format(np.array(cirq_results)))
cirq batch results: [[-0.66652703] [ 0.49764055] [ 0.67326665] [-0.95549959] [-0.81297827]]
همین عملیات در TFQ ساده شده است:
tfq.layers.Expectation()(circuit,
symbol_names=[a, b],
symbol_values=batch_vals,
operators=z0)
<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[-0.666526 ],
[ 0.49764216],
[ 0.6732664 ],
[-0.9554999 ],
[-0.8129788 ]], dtype=float32)>
2. بهینه سازی کوانتومی-کلاسیک ترکیبی
اکنون که اصول اولیه را دیدید، بیایید از TensorFlow Quantum برای ساخت یک شبکه عصبی کوانتومی کلاسیک ترکیبی استفاده کنیم. شما یک شبکه عصبی کلاسیک را برای کنترل یک کیوبیت آموزش خواهید داد. کنترل برای آماده سازی صحیح کیوبیت در حالت 0 یا 1 بهینه می شود و بر خطای کالیبراسیون سیستماتیک شبیه سازی شده غلبه می کند. این شکل معماری را نشان می دهد:
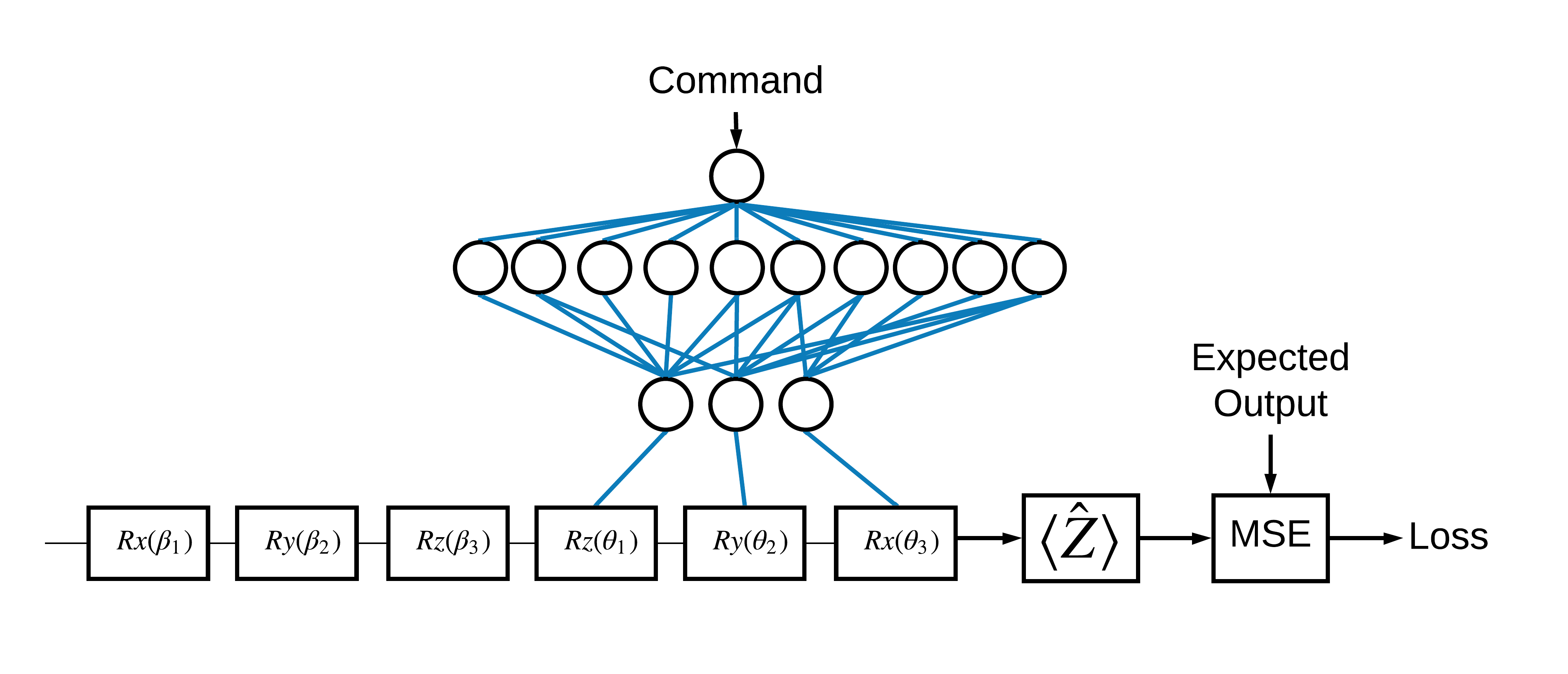
حتی بدون شبکه عصبی، این یک مشکل ساده برای حل است، اما موضوع مشابه مسائل کنترل کوانتومی واقعی است که ممکن است با استفاده از TFQ حل کنید. این یک مثال سرتاسری از یک محاسبات کلاسیک کوانتومی را با استفاده از tfq.layers.ControlledPQC (مدار کوانتومی پارامتریزهشده) در داخل یک tf.keras.Model نشان میدهد.
برای اجرای این آموزش، این معماری به 3 قسمت تقسیم شده است:
- مدار ورودی یا مدار نقطه داده: سه گیت اول \(R\) .
- مدار کنترل شده : سه دروازه دیگر \(R\) .
- کنترل کننده : شبکه عصبی کلاسیک که پارامترهای مدار کنترل شده را تنظیم می کند.
2.1 تعریف مدار کنترل شده
همانطور که در شکل بالا نشان داده شده است، یک چرخش تک بیتی قابل یادگیری را تعریف کنید. این با مدار کنترل شده ما مطابقت دارد.
# Parameters that the classical NN will feed values into.
control_params = sympy.symbols('theta_1 theta_2 theta_3')
# Create the parameterized circuit.
qubit = cirq.GridQubit(0, 0)
model_circuit = cirq.Circuit(
cirq.rz(control_params[0])(qubit),
cirq.ry(control_params[1])(qubit),
cirq.rx(control_params[2])(qubit))
SVGCircuit(model_circuit)
2.2 کنترل کننده
اکنون شبکه کنترلر را تعریف کنید:
# The classical neural network layers.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
با توجه به دسته ای از دستورات، کنترل کننده دسته ای از سیگنال های کنترلی را برای مدار کنترل شده خروجی می دهد.
کنترل کننده به طور تصادفی مقداردهی اولیه می شود، بنابراین این خروجی ها هنوز مفید نیستند.
controller(tf.constant([[0.0],[1.0]])).numpy()
array([[0. , 0. , 0. ],
[0.5815686 , 0.21376055, 0.57181627]], dtype=float32)
2.3 کنترلر را به مدار وصل کنید
از tfq برای اتصال کنترلر به مدار کنترل شده، به عنوان یک keras.Model استفاده کنید.
برای اطلاعات بیشتر در مورد این سبک از تعریف مدل، راهنمای Keras Functional API را ببینید.
ابتدا ورودی های مدل را تعریف کنید:
# This input is the simulated miscalibration that the model will learn to correct.
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.string,
name='circuits_input')
# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.float32,
name='commands_input')
سپس برای تعریف محاسبات، عملیات را روی آن ورودی ها اعمال کنید.
dense_2 = controller(commands_input)
# TFQ layer for classically controlled circuits.
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
# Observe Z
operators = cirq.Z(qubit))
expectation = expectation_layer([circuits_input, dense_2])
اکنون این محاسبات را به عنوان tf.keras.Model بسته بندی کنید:
# The full Keras model is built from our layers.
model = tf.keras.Model(inputs=[circuits_input, commands_input],
outputs=expectation)
معماری شبکه با نمودار مدل زیر نشان داده شده است. این نمودار مدل را با نمودار معماری مقایسه کنید تا صحت را تأیید کنید.
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
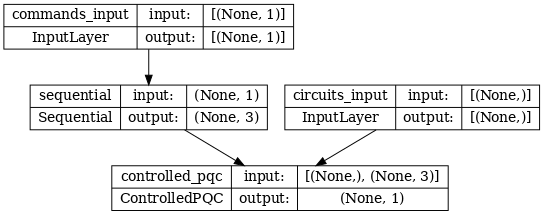
این مدل دو ورودی می گیرد: دستورات مربوط به کنترلر و مدار ورودی که کنترل کننده سعی در تصحیح خروجی آن دارد.
2.4 مجموعه داده
مدل تلاش میکند تا مقدار صحیح اندازهگیری \(\hat{Z}\) را برای هر دستور خروجی دهد. دستورات و مقادیر صحیح در زیر تعریف شده است.
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired Z expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
این کل مجموعه داده آموزشی برای این کار نیست. هر نقطه داده در مجموعه داده به یک مدار ورودی نیز نیاز دارد.
2.4 تعریف مدار ورودی
مدار ورودی زیر کالیبراسیون اشتباه تصادفی را تعریف می کند که مدل یاد می گیرد آن را اصلاح کند.
random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit(
cirq.rx(random_rotations[0])(qubit),
cirq.ry(random_rotations[1])(qubit),
cirq.rz(random_rotations[2])(qubit)
)
datapoint_circuits = tfq.convert_to_tensor([
noisy_preparation
] * 2) # Make two copied of this circuit
دو نسخه از مدار وجود دارد، یکی برای هر نقطه داده.
datapoint_circuits.shape
TensorShape([2])
2.5 آموزش
با ورودی های تعریف شده می توانید مدل tfq را آزمایش کنید.
model([datapoint_circuits, commands]).numpy()
array([[0.95853525],
[0.6272128 ]], dtype=float32)
اکنون یک فرآیند آموزشی استاندارد را اجرا کنید تا این مقادیر را نسبت به خروجی های expected_outputs تنظیم کنید.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss)
history = model.fit(x=[datapoint_circuits, commands],
y=expected_outputs,
epochs=30,
verbose=0)
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
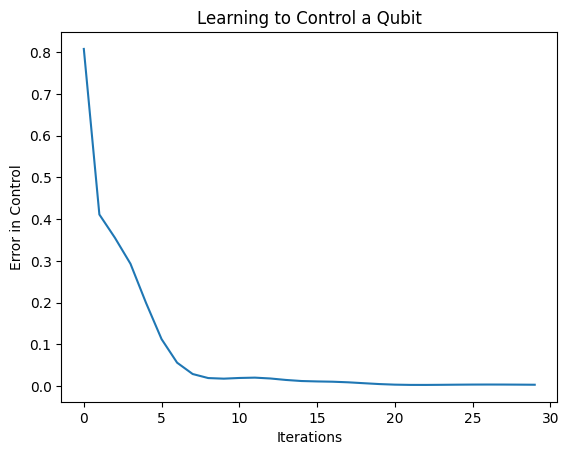
از این نمودار می توانید ببینید که شبکه عصبی یاد گرفته است بر کالیبراسیون اشتباه سیستماتیک غلبه کند.
2.6 بررسی خروجی ها
اکنون از مدل آموزش دیده برای تصحیح خطاهای کالیبراسیون کیوبیت استفاده کنید. با سیرک:
def check_error(command_values, desired_values):
"""Based on the value in `command_value` see how well you could prepare
the full circuit to have `desired_value` when taking expectation w.r.t. Z."""
params_to_prepare_output = controller(command_values).numpy()
full_circuit = noisy_preparation + model_circuit
# Test how well you can prepare a state to get expectation the expectation
# value in `desired_values`
for index in [0, 1]:
state = cirq_simulator.simulate(
full_circuit,
{s:v for (s,v) in zip(control_params, params_to_prepare_output[index])}
).final_state_vector
expt = cirq.Z(qubit).expectation_from_state_vector(state, {qubit: 0}).real
print(f'For a desired output (expectation) of {desired_values[index]} with'
f' noisy preparation, the controller\nnetwork found the following '
f'values for theta: {params_to_prepare_output[index]}\nWhich gives an'
f' actual expectation of: {expt}\n')
check_error(commands, expected_outputs)
For a desired output (expectation) of [1.] with noisy preparation, the controller network found the following values for theta: [-0.6788422 0.3395225 -0.59394693] Which gives an actual expectation of: 0.9171845316886902 For a desired output (expectation) of [-1.] with noisy preparation, the controller network found the following values for theta: [-5.203663 -0.29528576 3.2887425 ] Which gives an actual expectation of: -0.9511058330535889
ارزش تابع از دست دادن در طول آموزش، یک ایده تقریبی از چگونگی یادگیری مدل ارائه می دهد. هرچه ضرر کمتر باشد، مقادیر مورد انتظار در سلول بالا به desired_values است. اگر نگران مقادیر پارامتر نیستید، همیشه می توانید با استفاده از tfq خروجی ها را از بالا بررسی کنید:
model([datapoint_circuits, commands])
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[ 0.91718477],
[-0.9511056 ]], dtype=float32)>
3 آموزش آماده سازی حالت های ویژه اپراتورهای مختلف
انتخاب حالتهای ویژه \(\pm \hat{Z}\) مربوط به 1 و 0 دلخواه بود. شما میتوانید به همین راحتی بخواهید 1 با \(+ \hat{Z}\) eigenstate و 0 مطابق با \(-\hat{X}\) eigenstate مطابقت داشته باشد. یکی از راه های انجام این کار، تعیین یک عملگر اندازه گیری متفاوت برای هر دستور است، همانطور که در شکل زیر نشان داده شده است:
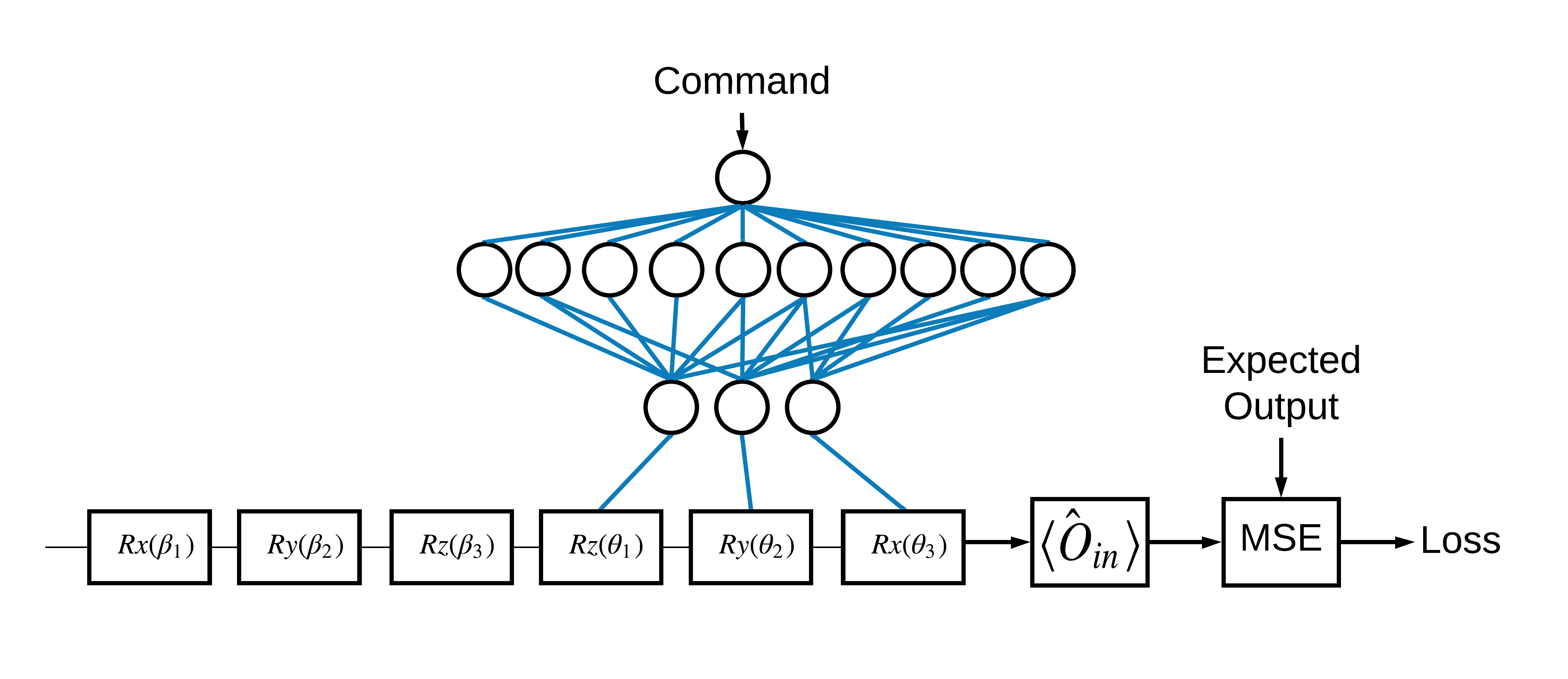
این نیاز به استفاده از tfq.layers.Expectation دارد. اکنون ورودی شما شامل سه شیء شده است: مدار، فرمان و اپراتور. خروجی همچنان مقدار مورد انتظار است.
3.1 تعریف مدل جدید
بیایید نگاهی به مدل برای انجام این کار بیندازیم:
# Define inputs.
commands_input = tf.keras.layers.Input(shape=(1),
dtype=tf.dtypes.float32,
name='commands_input')
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.dtypes.string,
name='circuits_input')
operators_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.string,
name='operators_input')
این هم شبکه کنترلر:
# Define classical NN.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
مدار و کنترلر را در یک keras tfq keras.Model
dense_2 = controller(commands_input)
# Since you aren't using a PQC or ControlledPQC you must append
# your model circuit onto the datapoint circuit tensor manually.
full_circuit = tfq.layers.AddCircuit()(circuits_input, append=model_circuit)
expectation_output = tfq.layers.Expectation()(full_circuit,
symbol_names=control_params,
symbol_values=dense_2,
operators=operators_input)
# Contruct your Keras model.
two_axis_control_model = tf.keras.Model(
inputs=[circuits_input, commands_input, operators_input],
outputs=[expectation_output])
3.2 مجموعه داده
اکنون همچنین اپراتورهایی را که می خواهید برای هر نقطه داده ای که برای model_circuit تهیه می کنید اندازه گیری کنید، اضافه کنید:
# The operators to measure, for each command.
operator_data = tfq.convert_to_tensor([[cirq.X(qubit)], [cirq.Z(qubit)]])
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
3.3 آموزش
اکنون که ورودی ها و خروجی های جدید خود را دارید، می توانید بار دیگر با استفاده از کراس تمرین کنید.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
two_axis_control_model.compile(optimizer=optimizer, loss=loss)
history = two_axis_control_model.fit(
x=[datapoint_circuits, commands, operator_data],
y=expected_outputs,
epochs=30,
verbose=1)
Epoch 1/30 1/1 [==============================] - 0s 320ms/step - loss: 2.4404 Epoch 2/30 1/1 [==============================] - 0s 3ms/step - loss: 1.8713 Epoch 3/30 1/1 [==============================] - 0s 3ms/step - loss: 1.1400 Epoch 4/30 1/1 [==============================] - 0s 3ms/step - loss: 0.5071 Epoch 5/30 1/1 [==============================] - 0s 3ms/step - loss: 0.1611 Epoch 6/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0426 Epoch 7/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0117 Epoch 8/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0032 Epoch 9/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0147 Epoch 10/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0452 Epoch 11/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0670 Epoch 12/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0648 Epoch 13/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0471 Epoch 14/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0289 Epoch 15/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0180 Epoch 16/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0138 Epoch 17/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0130 Epoch 18/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0137 Epoch 19/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0148 Epoch 20/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0156 Epoch 21/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0157 Epoch 22/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0149 Epoch 23/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0135 Epoch 24/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0119 Epoch 25/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0100 Epoch 26/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0082 Epoch 27/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0064 Epoch 28/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0047 Epoch 29/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0034 Epoch 30/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0024
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
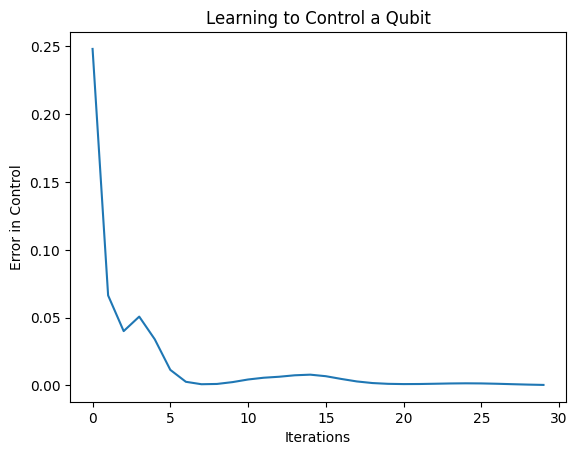
تابع ضرر به صفر رسیده است.
controller به عنوان یک مدل مستقل موجود است. با کنترلر تماس بگیرید و پاسخ آن به هر سیگنال فرمان را بررسی کنید. مقایسه صحیح این خروجی ها با محتویات چرخش های random_rotations به مقداری کار نیاز دارد.
controller.predict(np.array([0,1]))
array([[3.6335812 , 1.8470774 , 0.71675825],
[5.3085413 , 0.08116499, 2.8337662 ]], dtype=float32)
