RSVP for your your local TensorFlow Everywhere event today!

高级自动微分

在 TensorFlow.org 上查看 在 Google Colab 中运行 在 GitHub 上查看源代码 下载笔记本

自动微分指南包括计算梯度所需的全部内容。本文重点介绍 tf.GradientTape API 更深入、更不常见的功能。

设置

import tensorflow as tf

import matplotlib as mpl
import matplotlib.pyplot as plt

mpl.rcParams['figure.figsize'] = (8, 6)

控制梯度记录

在自动微分指南中，您已了解构建梯度计算时如何控制条带监视变量和张量。

条带还具有操作记录的方法。

如果您希望停止记录梯度，可以使用 GradientTape.stop_recording() 暂时挂起记录。

如果您不希望在模型中间对复杂运算微分，这可能有助于减少开销。其中可能包括计算指标或中间结果：

x = tf.Variable(2.0)
y = tf.Variable(3.0)

with tf.GradientTape() as t:
  x_sq = x * x
  with t.stop_recording():
    y_sq = y * y
  z = x_sq + y_sq

grad = t.gradient(z, {'x': x, 'y': y})

print('dz/dx:', grad['x'])  # 2*x => 4
print('dz/dy:', grad['y'])

dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None

如果您希望完全重新开始，请使用 reset()。通常，直接退出梯度带块并重新开始比较易于读取，但在退出梯度带块有困难或不可行时，可以使用 reset。

x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True

with tf.GradientTape() as t:
  y_sq = y * y
  if reset:
    # Throw out all the tape recorded so far
    t.reset()
  z = x * x + y_sq

grad = t.gradient(z, {'x': x, 'y': y})

print('dz/dx:', grad['x'])  # 2*x => 4
print('dz/dy:', grad['y'])

dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None

停止梯度

与上面的全局条带控制相比，tf.stop_gradient 函数更加精确。它可以用来阻止梯度沿着特定路径流动，而不需要访问条带本身：

x = tf.Variable(2.0)
y = tf.Variable(3.0)

with tf.GradientTape() as t:
  y_sq = y**2
  z = x**2 + tf.stop_gradient(y_sq)

grad = t.gradient(z, {'x': x, 'y': y})

print('dz/dx:', grad['x'])  # 2*x => 4
print('dz/dy:', grad['y'])

dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None

自定义梯度

在某些情况下，您可能需要精确控制梯度的计算方式，而不是使用默认值。这些情况包括：

  • 正在编写的新运算没有定义的梯度。
  • 默认计算在数值上不稳定。
  • 您希望从前向传递缓存开销大的计算。
  • 您想修改一个值（例如使用：tf.clip_by_value、tf.math.round）而不修改梯度。

对于编写新运算，您可以使用 tf.RegisterGradient 自行设置。请参阅其页面了解详细信息。（注意，梯度注册为全局，需谨慎更改。）

对于后三种情况，可以使用 tf.custom_gradient。

以下示例将 tf.clip_by_norm 应用于中间梯度。

# Establish an identity operation, but clip during the gradient pass
@tf.custom_gradient
def clip_gradients(y):
  def backward(dy):
    return tf.clip_by_norm(dy, 0.5)
  return y, backward

v = tf.Variable(2.0)
with tf.GradientTape() as t:
  output = clip_gradients(v * v)
print(t.gradient(output, v))  # calls "backward", which clips 4 to 2

tf.Tensor(2.0, shape=(), dtype=float32)

请参见 tf.custom_gradient 装饰器了解更多详细信息。

多个条带

多个条带无缝交互。例如，下面每个条带监视不同的张量集：

x0 = tf.constant(0.0)
x1 = tf.constant(0.0)

with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
  tape0.watch(x0)
  tape1.watch(x1)

  y0 = tf.math.sin(x0)
  y1 = tf.nn.sigmoid(x1)

  y = y0 + y1

  ys = tf.reduce_sum(y)

tape0.gradient(ys, x0).numpy()   # cos(x) => 1.0

1.0

tape1.gradient(ys, x1).numpy()   # sigmoid(x1)*(1-sigmoid(x1)) => 0.25

0.25

高阶梯度

GradientTape 上下文管理器内的运算会被记录下来，以供自动微分。如果在该上下文中计算梯度，梯度计算也会被记录。因此，完全相同的 API 也适用于高阶梯度。例如：

x = tf.Variable(1.0)  # Create a Tensorflow variable initialized to 1.0

with tf.GradientTape() as t2:
  with tf.GradientTape() as t1:
    y = x * x * x

  # Compute the gradient inside the outer `t2` context manager
  # which means the gradient computation is differentiable as well.
  dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)

print('dy_dx:', dy_dx.numpy())  # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy())  # 6 * x => 6.0

dy_dx: 3.0
d2y_dx2: 6.0

虽然这确实可以得到标量函数的二次导数，但这种模式并不能通用于生成黑塞矩阵，因为 GradientTape.gradient 只计算标量的梯度。要构造黑塞矩阵，请参见“雅可比矩阵”部分下的“黑塞矩阵”示例。

当您从梯度计算标量，然后产生的标量作为第二个梯度计算的源时，“嵌套调用 GradientTape.gradient”是一种不错的模式，如以下示例所示。

示例：输入梯度正则化

许多模型容易受到“对抗性示例”影响，这种技术的集合会修改模型的输入，进而混淆模型输出。最简单的实现沿着输出相对于输入的梯度（即“输入梯度”） 迈出一步。

一种增强相对于对抗性示例的稳健性的方法是输入梯度正则化，这种方法会尝试将输入梯度的幅度最小化。如果输入梯度较小，那么输出的变化也应该较小。

以下是输入梯度正则化的简单实现：

  1. 使用内条带计算输出相对于输入的梯度。
  2. 计算该输入梯度的幅度。
  3. 计算该幅度相对于模型的梯度。
x = tf.random.normal([7, 5])

layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)

with tf.GradientTape() as t2:
  # The inner tape only takes the gradient with respect to the input,
  # not the variables.
  with tf.GradientTape(watch_accessed_variables=False) as t1:
    t1.watch(x)
    y = layer(x)
    out = tf.reduce_sum(layer(x)**2)
  # 1. Calculate the input gradient.
  g1 = t1.gradient(out, x)
  # 2. Calculate the magnitude of the input gradient.
  g1_mag = tf.norm(g1)

# 3. Calculate the gradient of the magnitude with respect to the model.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)

[var.shape for var in dg1_mag]

[TensorShape([5, 10]), TensorShape([10])]

雅可比矩阵

以上所有示例都取标量目标相对于某些源张量的梯度。

雅可比矩阵代表向量值函数的梯度。每行都包含其中一个向量元素的梯度。

GradientTape.jacobian 方法让您能够有效计算雅可比矩阵。

注意：

  • 类似于 gradient：sources 参数可以是张量或张量的容器。
  • 不同于 gradient：target 张量必须是单个张量。

标量源

作为第一个示例，以下是矢量目标相对于标量源的雅可比矩阵。

x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)

with tf.GradientTape() as tape:
  y = tf.nn.sigmoid(x+delta)

dy_dx = tape.jacobian(y, delta)

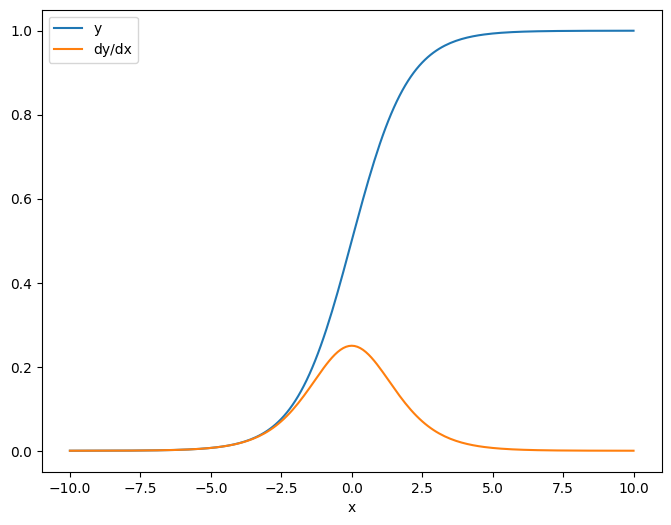
当您相对于标量取雅可比矩阵时，结果为目标的形状，并给出每个元素相对于源的梯度：

print(y.shape)
print(dy_dx.shape)

(201,)
(201,)


plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')

png

张量源

无论输入是标量还是张量，GradientTape.jacobian 都能有效计算源的每个元素相对于目标的每个元素的梯度。

例如，此层的输出的形状为 (10，7)。

x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)

with tf.GradientTape(persistent=True) as tape:
  y = layer(x)

y.shape

TensorShape([7, 10])

层内核的形状是 (5，10)。

layer.kernel.shape

TensorShape([5, 10])

将这两个形状连在一起就是输出相对于内核的雅可比矩阵的形状：

j = tape.jacobian(y, layer.kernel)
j.shape

TensorShape([7, 10, 5, 10])

如果您在目标的维度上求和，会得到由 GradientTape.gradient 计算的总和的梯度。

g = tape.gradient(y, layer.kernel)
print('g.shape:', g.shape)

j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)

g.shape: (5, 10)
delta: 2.3841858e-07

示例：黑塞矩阵

虽然 tf.GradientTape 并没有给出构造黑塞矩阵的显式方法，但可以使用 GradientTape.jacobian 方法进行构建。

注：黑塞矩阵包含 N**2 个参数。由于这个原因和其他原因，它对于大多数模型都不实际。此示例主要是为了演示如何使用 GradientTape.jacobian 方法，并不是对直接黑塞矩阵优化的认可。黑塞矩阵向量积可以通过嵌套条带有效计算，这也是一种更有效的二阶优化方法。

x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)

with tf.GradientTape() as t2:
  with tf.GradientTape() as t1:
    x = layer1(x)
    x = layer2(x)
    loss = tf.reduce_mean(x**2)

  g = t1.gradient(loss, layer1.kernel)

h = t2.jacobian(g, layer1.kernel)

print(f'layer.kernel.shape: {layer1.kernel.shape}')
print(f'h.shape: {h.shape}')

layer.kernel.shape: (5, 8)
h.shape: (5, 8, 5, 8)

要将此黑塞矩阵用于牛顿方法步骤，首先需要将其轴展平为矩阵，然后将梯度展平为向量：

n_params = tf.reduce_prod(layer1.kernel.shape)

g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])

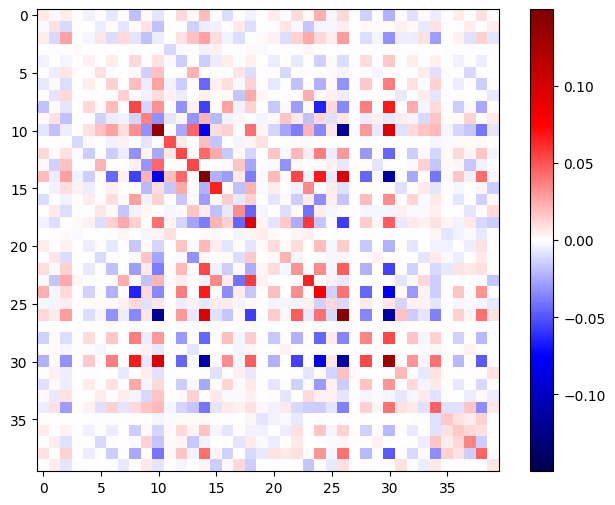
黑塞矩阵应当对称：

def imshow_zero_center(image, **kwargs):
  lim = tf.reduce_max(abs(image))
  plt.imshow(image, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
  plt.colorbar()

imshow_zero_center(h_mat)

png

牛顿方法更新步骤如下所示。

eps = 1e-3
eye_eps = tf.eye(h_mat.shape[0])*eps

注：实际上不反转矩阵。

# X(k+1) = X(k) - (∇²f(X(k)))^-1 @ ∇f(X(k))
# h_mat = ∇²f(X(k))
# g_vec = ∇f(X(k))
update = tf.linalg.solve(h_mat + eye_eps, g_vec)

# Reshape the update and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(update, layer1.kernel.shape))

虽然这对于单个 tf.Variable 来说相对简单，但将其应用于非平凡模型则需要仔细的级联和切片，以产生跨多个变量的完整黑塞矩阵。

批量雅可比矩阵

在某些情况下，您需要取各个目标堆栈相对于源堆栈的雅可比矩阵，其中每个目标-源对的雅可比矩阵都是独立的。

例如，此处的输入 x 形状为 (batch, ins) ，输出 y 形状为 (batch, outs)。

x = tf.random.normal([7, 5])

layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)

with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
  tape.watch(x)
  y = layer1(x)
  y = layer2(y)

y.shape

TensorShape([7, 6])

y 相对 x 的完整雅可比矩阵的形状为 (batch, ins, batch, outs)，即使您只想要 (batch, ins, outs)。

j = tape.jacobian(y, x)
j.shape

TensorShape([7, 6, 7, 5])

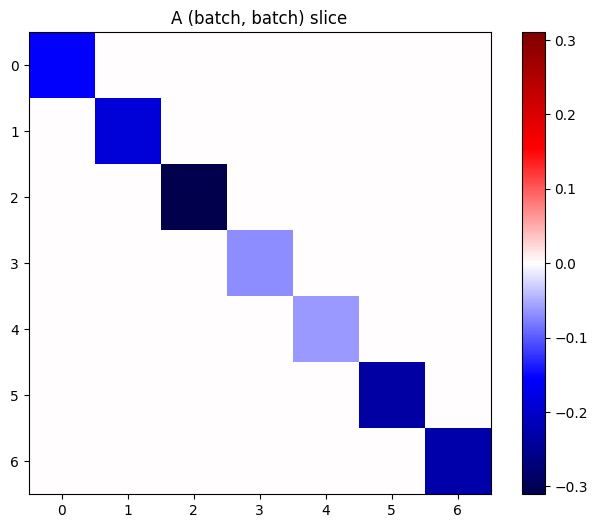
如果堆栈中各项的梯度相互独立，那么此张量的每一个 (batch, batch) 切片都是对角矩阵：

imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')

png

def plot_as_patches(j):
  # Reorder axes so the diagonals will each form a contiguous patch.
  j = tf.transpose(j, [1, 0, 3, 2])
  # Pad in between each patch.
  lim = tf.reduce_max(abs(j))
  j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
             constant_values=-lim)
  # Reshape to form a single image.
  s = j.shape
  j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
  imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])

plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')

png

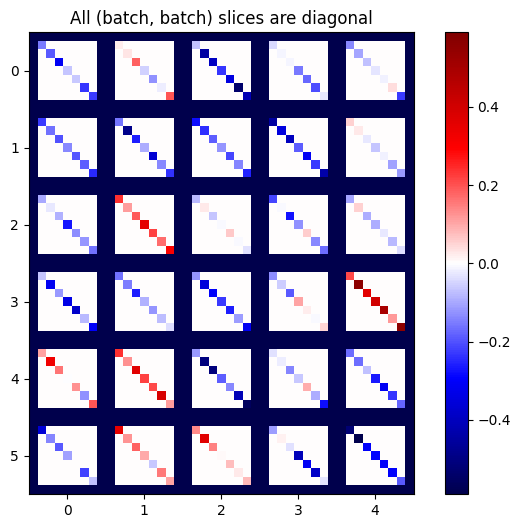
要获取所需结果，您可以对重复的 batch 维度求和，或者使用 tf.einsum 选择对角线。

j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.shape)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.shape)

(7, 6, 5)
(7, 6, 5)

没有额外维度时，计算会更加高效。GradientTape.batch_jacobian 方法就是如此运作的。

jb = tape.batch_jacobian(y, x)
jb.shape

WARNING:tensorflow:5 out of the last 5 calls to <function pfor.<locals>.f at 0x7f49b409ae18> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/tutorials/customization/performance#python_or_tensor_args and https://www.tensorflow.org/api_docs/python/tf/function for  more details.

TensorShape([7, 6, 5])

error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())

0.0

小心：GradientTape.batch_jacobian 只验证源和目标的第一维是否匹配，并不会检查梯度是否独立。用户需要确保仅在合理条件下使用 batch_jacobian。例如，添加 layers.BatchNormalization 将破坏独立性，因为它在 batch 维度进行了归一化：

x = tf.random.normal([7, 5])

layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)

with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
  tape.watch(x)
  y = layer1(x)
  y = bn(y, training=True)
  y = layer2(y)

j = tape.jacobian(y, x)
print(f'j.shape: {j.shape}')

WARNING:tensorflow:6 out of the last 6 calls to <function pfor.<locals>.f at 0x7f49b4232ea0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/tutorials/customization/performance#python_or_tensor_args and https://www.tensorflow.org/api_docs/python/tf/function for  more details.
j.shape: (7, 6, 7, 5)


plot_as_patches(j)

_ = plt.title('These slices are not diagonal')
_ = plt.xlabel("Don't use `batch_jacobian`")

png

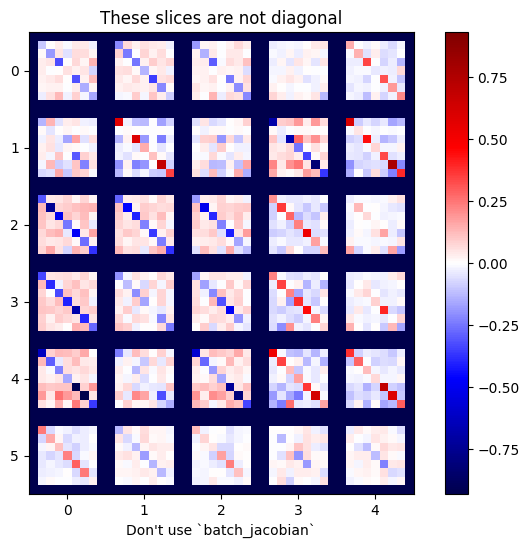
在此示例中，batch_jacobian 仍然可以运行并返回某些信息与预期形状，但其内容具有不明确的含义。

jb = tape.batch_jacobian(y, x)
print(f'jb.shape: {jb.shape}')

WARNING:tensorflow:7 out of the last 7 calls to <function pfor.<locals>.f at 0x7f49b41c8ae8> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/tutorials/customization/performance#python_or_tensor_args and https://www.tensorflow.org/api_docs/python/tf/function for  more details.
jb.shape: (7, 6, 5)