 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看 |
 在 Google Colab 中运行 在 Google Colab 中运行 |
 在 Github 上查看源代码 在 Github 上查看源代码 |
 下载笔记本 下载笔记本 |
在本 Colab 中,我们将探讨 TensorFlow Probability 的一些基本功能。
依赖项和前提条件
Import
from pprint import pprint
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
sns.reset_defaults()
sns.set_context(context='talk',font_scale=0.7)
plt.rcParams['image.cmap'] = 'viridis'
%matplotlib inline
tfd = tfp.distributions
tfb = tfp.bijectors
Utils
def print_subclasses_from_module(module, base_class, maxwidth=80):
import functools, inspect, sys
subclasses = [name for name, obj in inspect.getmembers(module)
if inspect.isclass(obj) and issubclass(obj, base_class)]
def red(acc, x):
if not acc or len(acc[-1]) + len(x) + 2 > maxwidth:
acc.append(x)
else:
acc[-1] += ", " + x
return acc
print('\n'.join(functools.reduce(red, subclasses, [])))
大纲
- TensorFlow
- TensorFlow Probability
- 分布
- Bijector
- MCMC
- ……等等!
前言:TensorFlow
TensorFlow 是一个科学计算库。
它支持
- 大量数学运算
- 高效的向量化计算
- 简单的硬件加速
- 自动微分
向量化
- 向量化可以提高计算速度
- 同时也意味着要对形状有更多考虑
mats = tf.random.uniform(shape=[1000, 10, 10])
vecs = tf.random.uniform(shape=[1000, 10, 1])
def for_loop_solve():
return np.array(
[tf.linalg.solve(mats[i, ...], vecs[i, ...]) for i in range(1000)])
def vectorized_solve():
return tf.linalg.solve(mats, vecs)
# Vectorization for the win!
%timeit for_loop_solve()
%timeit vectorized_solve()
1 loops, best of 3: 2 s per loop 1000 loops, best of 3: 653 µs per loop
硬件加速
# Code can run seamlessly on a GPU, just change Colab runtime type
# in the 'Runtime' menu.
if tf.test.gpu_device_name() == '/device:GPU:0':
print("Using a GPU")
else:
print("Using a CPU")
Using a CPU
自动微分
a = tf.constant(np.pi)
b = tf.constant(np.e)
with tf.GradientTape() as tape:
tape.watch([a, b])
c = .5 * (a**2 + b**2)
grads = tape.gradient(c, [a, b])
print(grads[0])
print(grads[1])
tf.Tensor(3.1415927, shape=(), dtype=float32) tf.Tensor(2.7182817, shape=(), dtype=float32)
TensorFlow Probability
TensorFlow Probability 是 TensorFlow 中的一个用于概率推理和统计分析的库。
通过低级模块化组件的组合为建模、推断和批判提供支持。
低级构建块
- 分布
- Bijector
高级构造
- 马尔可夫链蒙特卡洛
- 概率层
- 结构化时间数列
- 广义线性模型
- 优化器
分布
tfp.distributions.Distribution 是具有两个核心方法的类:sample 和 log_prob。
TFP 有很多分布!
print_subclasses_from_module(tfp.distributions, tfp.distributions.Distribution)
Autoregressive, BatchReshape, Bates, Bernoulli, Beta, BetaBinomial, Binomial Blockwise, Categorical, Cauchy, Chi, Chi2, CholeskyLKJ, ContinuousBernoulli Deterministic, Dirichlet, DirichletMultinomial, Distribution, DoublesidedMaxwell Empirical, ExpGamma, ExpRelaxedOneHotCategorical, Exponential, FiniteDiscrete Gamma, GammaGamma, GaussianProcess, GaussianProcessRegressionModel GeneralizedNormal, GeneralizedPareto, Geometric, Gumbel, HalfCauchy, HalfNormal HalfStudentT, HiddenMarkovModel, Horseshoe, Independent, InverseGamma InverseGaussian, JohnsonSU, JointDistribution, JointDistributionCoroutine JointDistributionCoroutineAutoBatched, JointDistributionNamed JointDistributionNamedAutoBatched, JointDistributionSequential JointDistributionSequentialAutoBatched, Kumaraswamy, LKJ, Laplace LinearGaussianStateSpaceModel, LogLogistic, LogNormal, Logistic, LogitNormal Mixture, MixtureSameFamily, Moyal, Multinomial, MultivariateNormalDiag MultivariateNormalDiagPlusLowRank, MultivariateNormalFullCovariance MultivariateNormalLinearOperator, MultivariateNormalTriL MultivariateStudentTLinearOperator, NegativeBinomial, Normal, OneHotCategorical OrderedLogistic, PERT, Pareto, PixelCNN, PlackettLuce, Poisson PoissonLogNormalQuadratureCompound, PowerSpherical, ProbitBernoulli QuantizedDistribution, RelaxedBernoulli, RelaxedOneHotCategorical, Sample SinhArcsinh, SphericalUniform, StudentT, StudentTProcess TransformedDistribution, Triangular, TruncatedCauchy, TruncatedNormal, Uniform VariationalGaussianProcess, VectorDeterministic, VonMises VonMisesFisher, Weibull, WishartLinearOperator, WishartTriL, Zipf
一个简单的标量变量 Distribution
# A standard normal
normal = tfd.Normal(loc=0., scale=1.)
print(normal)
tfp.distributions.Normal("Normal", batch_shape=[], event_shape=[], dtype=float32)
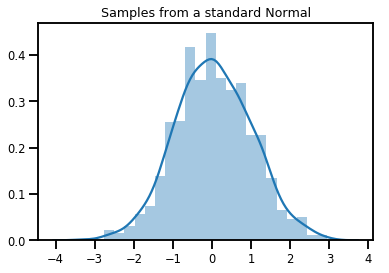
# Plot 1000 samples from a standard normal
samples = normal.sample(1000)
sns.distplot(samples)
plt.title("Samples from a standard Normal")
plt.show()
# Compute the log_prob of a point in the event space of `normal`
normal.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
# Compute the log_prob of a few points
normal.log_prob([-1., 0., 1.])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.4189385, -0.9189385, -1.4189385], dtype=float32)>
分布和形状
NumPy ndarrays 和 TensorFlow Tensors 包含形状。
TensorFlow Probability Distributions 包含形状语义。我们将形状划分为语义上不同的部分,不过,所有形状使用的是同一内存块 (Tensor/ndarray)。
- 批次形状表示具有不同参数的
Distribution的集合 - 事件形状表示
Distribution的样本的形状。
我们一般将批次形状放在“左侧”,而将事件形状放在“右侧”。
一个批次的标量变量 Distribution
批次就像“向量化”分布:计算并行发生的独立实例。
# Create a batch of 3 normals, and plot 1000 samples from each
normals = tfd.Normal([-2.5, 0., 2.5], 1.) # The scale parameter broadacasts!
print("Batch shape:", normals.batch_shape)
print("Event shape:", normals.event_shape)
Batch shape: (3,) Event shape: ()
# Samples' shapes go on the left!
samples = normals.sample(1000)
print("Shape of samples:", samples.shape)
Shape of samples: (1000, 3)
# Sample shapes can themselves be more complicated
print("Shape of samples:", normals.sample([10, 10, 10]).shape)
Shape of samples: (10, 10, 10, 3)
# A batch of normals gives a batch of log_probs.
print(normals.log_prob([-2.5, 0., 2.5]))
tf.Tensor([-0.9189385 -0.9189385 -0.9189385], shape=(3,), dtype=float32)
# The computation broadcasts, so a batch of normals applied to a scalar
# also gives a batch of log_probs.
print(normals.log_prob(0.))
tf.Tensor([-4.0439386 -0.9189385 -4.0439386], shape=(3,), dtype=float32)
# Normal numpy-like broadcasting rules apply!
xs = np.linspace(-6, 6, 200)
try:
normals.log_prob(xs)
except Exception as e:
print("TFP error:", e.message)
TFP error: Incompatible shapes: [200] vs. [3] [Op:SquaredDifference]
# That fails for the same reason this does:
try:
np.zeros(200) + np.zeros(3)
except Exception as e:
print("Numpy error:", e)
Numpy error: operands could not be broadcast together with shapes (200,) (3,)
# But this would work:
a = np.zeros([200, 1]) + np.zeros(3)
print("Broadcast shape:", a.shape)
Broadcast shape: (200, 3)
# And so will this!
xs = np.linspace(-6, 6, 200)[..., np.newaxis]
# => shape = [200, 1]
lps = normals.log_prob(xs)
print("Broadcast log_prob shape:", lps.shape)
Broadcast log_prob shape: (200, 3)
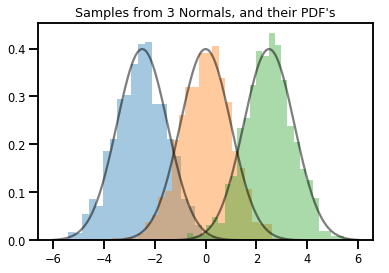
# Summarizing visually
for i in range(3):
sns.distplot(samples[:, i], kde=False, norm_hist=True)
plt.plot(np.tile(xs, 3), normals.prob(xs), c='k', alpha=.5)
plt.title("Samples from 3 Normals, and their PDF's")
plt.show()
一个向量变量 Distribution
mvn = tfd.MultivariateNormalDiag(loc=[0., 0.], scale_diag = [1., 1.])
print("Batch shape:", mvn.batch_shape)
print("Event shape:", mvn.event_shape)
Batch shape: () Event shape: (2,)
samples = mvn.sample(1000)
print("Samples shape:", samples.shape)
Samples shape: (1000, 2)
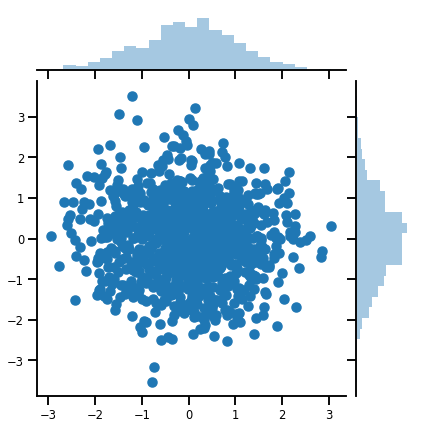
g = sns.jointplot(x=samples[:, 0], y=samples[:, 1], kind='scatter')
plt.show()
一个矩阵变量 Distribution
lkj = tfd.LKJ(dimension=10, concentration=[1.5, 3.0])
print("Batch shape: ", lkj.batch_shape)
print("Event shape: ", lkj.event_shape)
Batch shape: (2,) Event shape: (10, 10)
samples = lkj.sample()
print("Samples shape: ", samples.shape)
Samples shape: (2, 10, 10)
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(6, 3))
sns.heatmap(samples[0, ...], ax=axes[0], cbar=False)
sns.heatmap(samples[1, ...], ax=axes[1], cbar=False)
fig.tight_layout()
plt.show()
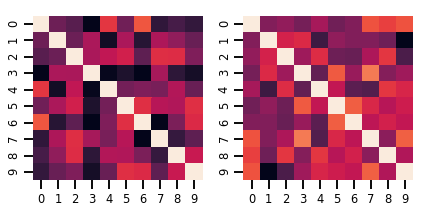
高斯过程
kernel = tfp.math.psd_kernels.ExponentiatedQuadratic()
xs = np.linspace(-5., 5., 200).reshape([-1, 1])
gp = tfd.GaussianProcess(kernel, index_points=xs)
print("Batch shape:", gp.batch_shape)
print("Event shape:", gp.event_shape)
Batch shape: () Event shape: (200,)
upper, lower = gp.mean() + [2 * gp.stddev(), -2 * gp.stddev()]
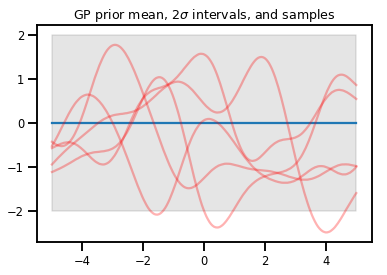
plt.plot(xs, gp.mean())
plt.fill_between(xs[..., 0], upper, lower, color='k', alpha=.1)
for _ in range(5):
plt.plot(xs, gp.sample(), c='r', alpha=.3)
plt.title(r"GP prior mean, $2\sigma$ intervals, and samples")
plt.show()
# *** Bonus question ***
# Why do so many of these functions lie outside the 95% intervals?
GP 回归
# Suppose we have some observed data
obs_x = [[-3.], [0.], [2.]] # Shape 3x1 (3 1-D vectors)
obs_y = [3., -2., 2.] # Shape 3 (3 scalars)
gprm = tfd.GaussianProcessRegressionModel(kernel, xs, obs_x, obs_y)
upper, lower = gprm.mean() + [2 * gprm.stddev(), -2 * gprm.stddev()]
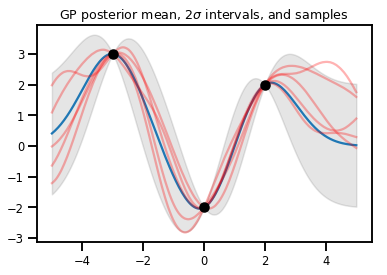
plt.plot(xs, gprm.mean())
plt.fill_between(xs[..., 0], upper, lower, color='k', alpha=.1)
for _ in range(5):
plt.plot(xs, gprm.sample(), c='r', alpha=.3)
plt.scatter(obs_x, obs_y, c='k', zorder=3)
plt.title(r"GP posterior mean, $2\sigma$ intervals, and samples")
plt.show()
Bijector
Bijector 代表(主要)可逆的平滑函数。这些函数可用于变换分布,同时保留获取样本和计算 log_prob 的能力。它们可以包含在 tfp.bijectors 模块中。
每个 Bijector 至少实现 3 个方法:
forward,inverse,forward_log_det_jacobian和inverse_log_det_jacobian之一(至少)。
凭借这些要素,我们可以变换分布,还可以从结果获取样本和对数概率!
数学方面的内容略显混乱
- \(X\) 是概率密度函数 \(p(x)\) 的一个随机变量
- \(g\) 是 \(X\) 空间上的一个可逆平滑函数
- \(Y = g(X)\) 是一个新的变换随机变量
- \(p(Y=y) = p(X=g^{-1}(y)) \cdot |\nabla g^{-1}(y)|\)
缓存
Bijector 还会缓存正向和反向计算以及 log-det-Jacobian,这让我们可以保存可能非常消耗资源的重复运算!
print_subclasses_from_module(tfp.bijectors, tfp.bijectors.Bijector)
AbsoluteValue, Affine, AffineLinearOperator, AffineScalar, BatchNormalization Bijector, Blockwise, Chain, CholeskyOuterProduct, CholeskyToInvCholesky CorrelationCholesky, Cumsum, DiscreteCosineTransform, Exp, Expm1, FFJORD FillScaleTriL, FillTriangular, FrechetCDF, GeneralizedExtremeValueCDF GeneralizedPareto, GompertzCDF, GumbelCDF, Identity, Inline, Invert IteratedSigmoidCentered, KumaraswamyCDF, LambertWTail, Log, Log1p MaskedAutoregressiveFlow, MatrixInverseTriL, MatvecLU, MoyalCDF, NormalCDF Ordered, Pad, Permute, PowerTransform, RationalQuadraticSpline, RayleighCDF RealNVP, Reciprocal, Reshape, Scale, ScaleMatvecDiag, ScaleMatvecLU ScaleMatvecLinearOperator, ScaleMatvecTriL, ScaleTriL, Shift, ShiftedGompertzCDF Sigmoid, Sinh, SinhArcsinh, SoftClip, Softfloor, SoftmaxCentered, Softplus Softsign, Split, Square, Tanh, TransformDiagonal, Transpose, WeibullCDF
一个简单的 Bijector
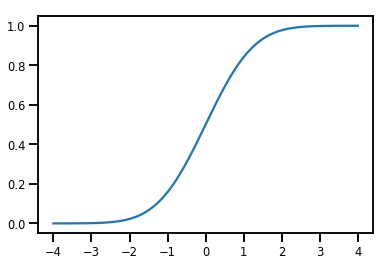
normal_cdf = tfp.bijectors.NormalCDF()
xs = np.linspace(-4., 4., 200)
plt.plot(xs, normal_cdf.forward(xs))
plt.show()
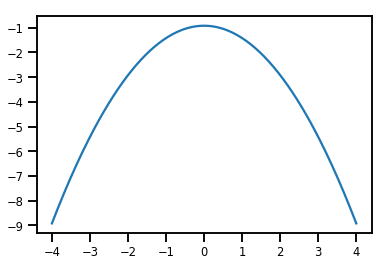
plt.plot(xs, normal_cdf.forward_log_det_jacobian(xs, event_ndims=0))
plt.show()
一个用于变换 Distribution 的Bijector
exp_bijector = tfp.bijectors.Exp()
log_normal = exp_bijector(tfd.Normal(0., .5))
samples = log_normal.sample(1000)
xs = np.linspace(1e-10, np.max(samples), 200)
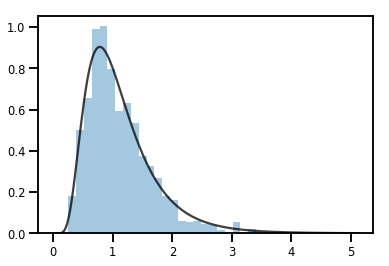
sns.distplot(samples, norm_hist=True, kde=False)
plt.plot(xs, log_normal.prob(xs), c='k', alpha=.75)
plt.show()
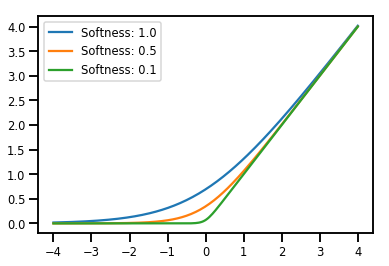
Bijector 批处理
# Create a batch of bijectors of shape [3,]
softplus = tfp.bijectors.Softplus(
hinge_softness=[1., .5, .1])
print("Hinge softness shape:", softplus.hinge_softness.shape)
Hinge softness shape: (3,)
# For broadcasting, we want this to be shape [200, 1]
xs = np.linspace(-4., 4., 200)[..., np.newaxis]
ys = softplus.forward(xs)
print("Forward shape:", ys.shape)
Forward shape: (200, 3)
# Visualization
lines = plt.plot(np.tile(xs, 3), ys)
for line, hs in zip(lines, softplus.hinge_softness):
line.set_label("Softness: %1.1f" % hs)
plt.legend()
plt.show()
缓存
# This bijector represents a matrix outer product on the forward pass,
# and a cholesky decomposition on the inverse pass. The latter costs O(N^3)!
bij = tfb.CholeskyOuterProduct()
size = 2500
# Make a big, lower-triangular matrix
big_lower_triangular = tf.eye(size)
# Squaring it gives us a positive-definite matrix
big_positive_definite = bij.forward(big_lower_triangular)
# Caching for the win!
%timeit bij.inverse(big_positive_definite)
%timeit tf.linalg.cholesky(big_positive_definite)
10000 loops, best of 3: 114 µs per loop 1 loops, best of 3: 208 ms per loop
MCMC
TFP 为某些标准马尔可夫链蒙特卡洛算法(汉密尔顿蒙特卡洛算法)提供了内置支持。
生成数据集
# Generate some data
def f(x, w):
# Pad x with 1's so we can add bias via matmul
x = tf.pad(x, [[1, 0], [0, 0]], constant_values=1)
linop = tf.linalg.LinearOperatorFullMatrix(w[..., np.newaxis])
result = linop.matmul(x, adjoint=True)
return result[..., 0, :]
num_features = 2
num_examples = 50
noise_scale = .5
true_w = np.array([-1., 2., 3.])
xs = np.random.uniform(-1., 1., [num_features, num_examples])
ys = f(xs, true_w) + np.random.normal(0., noise_scale, size=num_examples)
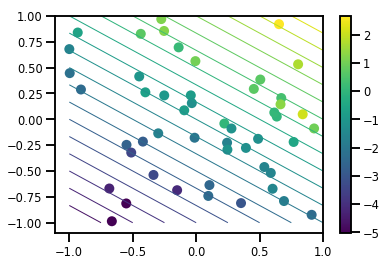
# Visualize the data set
plt.scatter(*xs, c=ys, s=100, linewidths=0)
grid = np.meshgrid(*([np.linspace(-1, 1, 100)] * 2))
xs_grid = np.stack(grid, axis=0)
fs_grid = f(xs_grid.reshape([num_features, -1]), true_w)
fs_grid = np.reshape(fs_grid, [100, 100])
plt.colorbar()
plt.contour(xs_grid[0, ...], xs_grid[1, ...], fs_grid, 20, linewidths=1)
plt.show()
定义 joint_log_prob 函数
非归一化后验概率分布是封闭数据的结果,用于构成联合对数概率的部分应用。
# Define the joint_log_prob function, and our unnormalized posterior.
def joint_log_prob(w, x, y):
# Our model in maths is
# w ~ MVN([0, 0, 0], diag([1, 1, 1]))
# y_i ~ Normal(w @ x_i, noise_scale), i=1..N
rv_w = tfd.MultivariateNormalDiag(
loc=np.zeros(num_features + 1),
scale_diag=np.ones(num_features + 1))
rv_y = tfd.Normal(f(x, w), noise_scale)
return (rv_w.log_prob(w) +
tf.reduce_sum(rv_y.log_prob(y), axis=-1))
# Create our unnormalized target density by currying x and y from the joint.
def unnormalized_posterior(w):
return joint_log_prob(w, xs, ys)
构建 HMC TransitionKernel 并调用 sample_chain
# Create an HMC TransitionKernel
hmc_kernel = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unnormalized_posterior,
step_size=np.float64(.1),
num_leapfrog_steps=2)
# We wrap sample_chain in tf.function, telling TF to precompile a reusable
# computation graph, which will dramatically improve performance.
@tf.function
def run_chain(initial_state, num_results=1000, num_burnin_steps=500):
return tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=hmc_kernel,
trace_fn=lambda current_state, kernel_results: kernel_results)
initial_state = np.zeros(num_features + 1)
samples, kernel_results = run_chain(initial_state)
print("Acceptance rate:", kernel_results.is_accepted.numpy().mean())
Acceptance rate: 0.915
结果不是太好!我们希望接受率接近 0.65。
(请参阅“Optimal Scaling for Various Metropolis-Hastings Algorithms”,Roberts 和 Rosenthal,2001 年)
自适应步长
我们可以将 HMC TransitionKernel 封装在 SimpleStepSizeAdaptation“元内核”中,而这将在 burnin 阶段应用一些(非常简单的启发式)逻辑来调整 HMC 步长。我们分配 80% 的 burnin 来调整步长,而让剩余的 20% 执行混合。
# Apply a simple step size adaptation during burnin
@tf.function
def run_chain(initial_state, num_results=1000, num_burnin_steps=500):
adaptive_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
hmc_kernel,
num_adaptation_steps=int(.8 * num_burnin_steps),
target_accept_prob=np.float64(.65))
return tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=adaptive_kernel,
trace_fn=lambda cs, kr: kr)
samples, kernel_results = run_chain(
initial_state=np.zeros(num_features+1))
print("Acceptance rate:", kernel_results.inner_results.is_accepted.numpy().mean())
Acceptance rate: 0.634
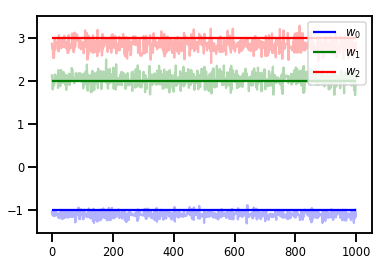
# Trace plots
colors = ['b', 'g', 'r']
for i in range(3):
plt.plot(samples[:, i], c=colors[i], alpha=.3)
plt.hlines(true_w[i], 0, 1000, zorder=4, color=colors[i], label="$w_{}$".format(i))
plt.legend(loc='upper right')
plt.show()
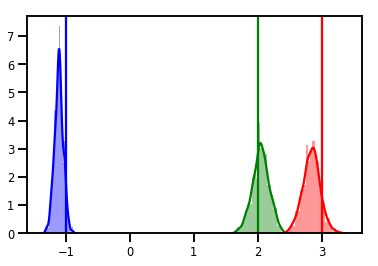
# Histogram of samples
for i in range(3):
sns.distplot(samples[:, i], color=colors[i])
ymax = plt.ylim()[1]
for i in range(3):
plt.vlines(true_w[i], 0, ymax, color=colors[i])
plt.ylim(0, ymax)
plt.show()
诊断
跟踪图的效果不错,但诊断的作用更大!
首先,我们需要运行多个链。这就像提供一批 initial_state 张量一样简单。
# Instead of a single set of initial w's, we create a batch of 8.
num_chains = 8
initial_state = np.zeros([num_chains, num_features + 1])
chains, kernel_results = run_chain(initial_state)
r_hat = tfp.mcmc.potential_scale_reduction(chains)
print("Acceptance rate:", kernel_results.inner_results.is_accepted.numpy().mean())
print("R-hat diagnostic (per latent variable):", r_hat.numpy())
Acceptance rate: 0.59175 R-hat diagnostic (per latent variable): [0.99998395 0.99932185 0.9997064 ]
噪声比例采样
# Define the joint_log_prob function, and our unnormalized posterior.
def joint_log_prob(w, sigma, x, y):
# Our model in maths is
# w ~ MVN([0, 0, 0], diag([1, 1, 1]))
# y_i ~ Normal(w @ x_i, noise_scale), i=1..N
rv_w = tfd.MultivariateNormalDiag(
loc=np.zeros(num_features + 1),
scale_diag=np.ones(num_features + 1))
rv_sigma = tfd.LogNormal(np.float64(1.), np.float64(5.))
rv_y = tfd.Normal(f(x, w), sigma[..., np.newaxis])
return (rv_w.log_prob(w) +
rv_sigma.log_prob(sigma) +
tf.reduce_sum(rv_y.log_prob(y), axis=-1))
# Create our unnormalized target density by currying x and y from the joint.
def unnormalized_posterior(w, sigma):
return joint_log_prob(w, sigma, xs, ys)
# Create an HMC TransitionKernel
hmc_kernel = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unnormalized_posterior,
step_size=np.float64(.1),
num_leapfrog_steps=4)
# Create a TransformedTransitionKernl
transformed_kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc_kernel,
bijector=[tfb.Identity(), # w
tfb.Invert(tfb.Softplus())]) # sigma
# Apply a simple step size adaptation during burnin
@tf.function
def run_chain(initial_state, num_results=1000, num_burnin_steps=500):
adaptive_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
transformed_kernel,
num_adaptation_steps=int(.8 * num_burnin_steps),
target_accept_prob=np.float64(.75))
return tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=adaptive_kernel,
seed=(0, 1),
trace_fn=lambda cs, kr: kr)
# Instead of a single set of initial w's, we create a batch of 8.
num_chains = 8
initial_state = [np.zeros([num_chains, num_features + 1]),
.54 * np.ones([num_chains], dtype=np.float64)]
chains, kernel_results = run_chain(initial_state)
r_hat = tfp.mcmc.potential_scale_reduction(chains)
print("Acceptance rate:", kernel_results.inner_results.inner_results.is_accepted.numpy().mean())
print("R-hat diagnostic (per w variable):", r_hat[0].numpy())
print("R-hat diagnostic (sigma):", r_hat[1].numpy())
Acceptance rate: 0.715875 R-hat diagnostic (per w variable): [1.0000073 1.00458208 1.00450512] R-hat diagnostic (sigma): 1.0092056996149859
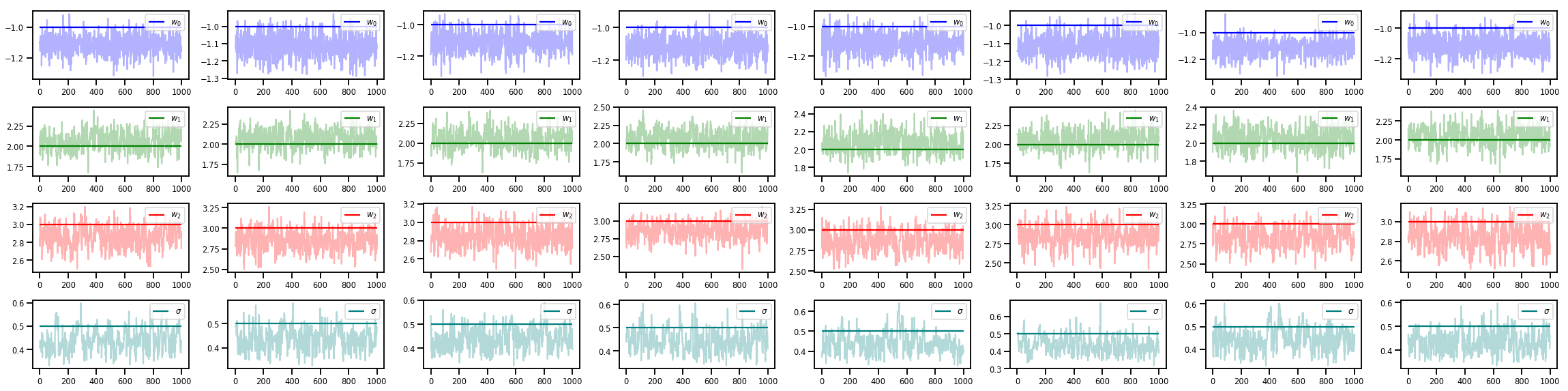
w_chains, sigma_chains = chains
# Trace plots of w (one of 8 chains)
colors = ['b', 'g', 'r', 'teal']
fig, axes = plt.subplots(4, num_chains, figsize=(4 * num_chains, 8))
for j in range(num_chains):
for i in range(3):
ax = axes[i][j]
ax.plot(w_chains[:, j, i], c=colors[i], alpha=.3)
ax.hlines(true_w[i], 0, 1000, zorder=4, color=colors[i], label="$w_{}$".format(i))
ax.legend(loc='upper right')
ax = axes[3][j]
ax.plot(sigma_chains[:, j], alpha=.3, c=colors[3])
ax.hlines(noise_scale, 0, 1000, zorder=4, color=colors[3], label=r"$\sigma$".format(i))
ax.legend(loc='upper right')
fig.tight_layout()
plt.show()
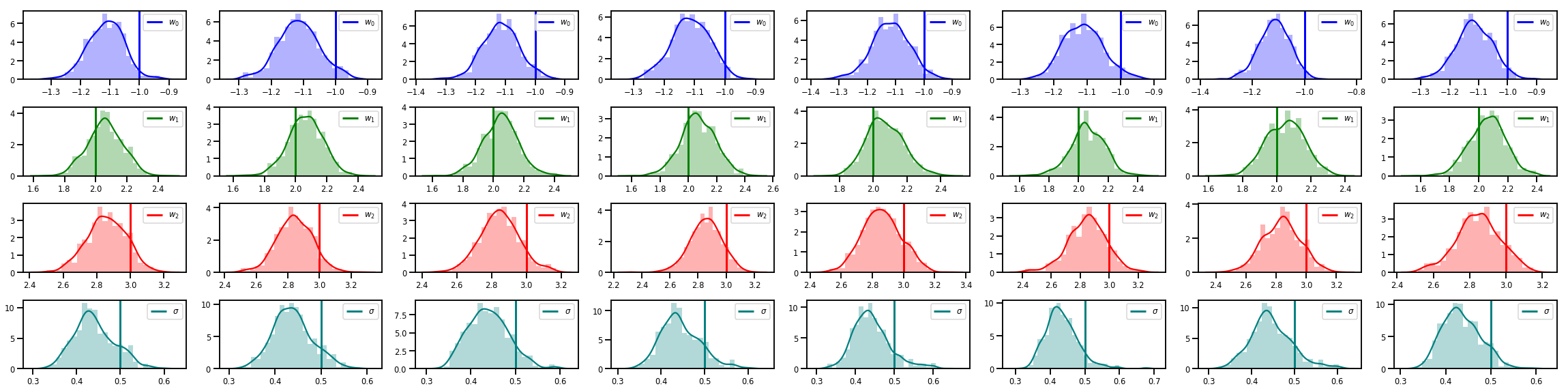
# Histogram of samples of w
fig, axes = plt.subplots(4, num_chains, figsize=(4 * num_chains, 8))
for j in range(num_chains):
for i in range(3):
ax = axes[i][j]
sns.distplot(w_chains[:, j, i], color=colors[i], norm_hist=True, ax=ax, hist_kws={'alpha': .3})
for i in range(3):
ax = axes[i][j]
ymax = ax.get_ylim()[1]
ax.vlines(true_w[i], 0, ymax, color=colors[i], label="$w_{}$".format(i), linewidth=3)
ax.set_ylim(0, ymax)
ax.legend(loc='upper right')
ax = axes[3][j]
sns.distplot(sigma_chains[:, j], color=colors[3], norm_hist=True, ax=ax, hist_kws={'alpha': .3})
ymax = ax.get_ylim()[1]
ax.vlines(noise_scale, 0, ymax, color=colors[3], label=r"$\sigma$".format(i), linewidth=3)
ax.set_ylim(0, ymax)
ax.legend(loc='upper right')
fig.tight_layout()
plt.show()
其他学习资源!
请查看下面这些有趣的博文和示例:
我们在 GitHub 上提供了更多示例和笔记本,请点击此处查看!
