 TensorFlow.org で表示 TensorFlow.org で表示 |
 Google Colab で実行 Google Colab で実行 |
 GitHub でソースを表示 GitHub でソースを表示 |
 ノートブックをダウンロード ノートブックをダウンロード |
JAX の TensorFlow Probability (TFP) に、分散数値計算用のツールが追加されました。多数のアクセラレータに拡張するために、ツールは「単一プログラム複数データ」パラダイム(SPMD)を使用してコードを記述することを中心に構築されています。
このノートブックでは、「SPMD で考える」方法を説明し、TPU ポッドや GPU のクラスタなどの構成にスケーリングするための新しい TFP 抽象化を紹介します。このコードを自分で実行する場合は、必ず TPU ランタイムを選択してください。
まず、最新バージョンの TFP、JAX、TF をインストールします。
Installs
pip install jaxlib --upgrade -q 2>&1 1> /dev/nullpip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/nullpip install tf-nightly-cpu -q -I 2>&1 1> /dev/nullpip install jax -I -q --upgrade 2>&1 1>/dev/null
いくつかの JAX ユーティリティと一般的なライブラリをインポートします。
Setup and Imports
import functools
import collections
import contextlib
import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds
from tensorflow_probability.substrates import jax as tfp
sns.set(style='white')
INFO:tensorflow:Enabling eager execution INFO:tensorflow:Enabling v2 tensorshape INFO:tensorflow:Enabling resource variables INFO:tensorflow:Enabling tensor equality INFO:tensorflow:Enabling control flow v2
また、いくつかの便利な TFP エイリアスを設定します。新しい抽象化は現在、tfp.experimental.distribute と tfp.experimental.mcmc で提供されています。
tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc
Root = tfed.JointDistributionCoroutine.Root
ノートブックを TPU に接続するには、JAX の次のヘルパーを使用します。接続されていることを確認するために、デバイスの数を出力します。これは 8 である必要があります。
from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')
Found 8 devices
jax.pmap の簡単な紹介
TPU に接続すると、8 台のデバイスにアクセスできるようになります。ただし、JAXコードを eager に実行すると、JAX はデフォルトで 1 台だけで計算を実行します。
多くのデバイス間で計算を実行する最も簡単な方法は、関数をマップし、各デバイスにマップの 1 つのインデックスを実行させることです。JAX は、関数を複数のデバイスにマップする関数に変換する jax.pmap (「並列マップ」)変換を提供します。
次の例では、サイズ 8 の配列を作成し(使用可能なデバイスの数に一致させるため)、それに 5 を追加する関数をマップします。
xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)
<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5. 6. 7. 8. 9. 10. 11. 12.]
ShardedDeviceArray 型が返され、出力配列がデバイス間で物理的に分割されていることを示していることに注目してください。
jax.pmap は意味的にマップのように機能しますが、その動作を変更するいくつかの重要なオプションがあります。デフォルトでは、pmap は関数へのすべての入力がマップされていると想定していますが、in_axes 引数を使用してこの動作を変更できます。
xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)
[ 5. 6. 7. 8. 9. 10. 11. 12.]
同様に、pmap の out_axes 引数は、すべてのデバイスで値を返すかどうかを決定します。out_axes を None に設定すると、最初のデバイスの値が自動的に返されます。値がすべてのデバイスで同じであると確信できる場合にのみ使用してください。
xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)
2.0
実行したいことがマップされた純粋関数として簡単に表現できない場合はどうなるでしょうか。たとえば、マッピングしている軸全体で合計を計算したい場合はどうなるでしょうか。JAX は、デバイス間で通信する「集合」機能を提供し、より興味深く複雑な分散プログラムを作成できるようにします。それらがどのように機能するかを説明するために、SPMD を紹介します。
SPMD とは
シングルプログラムマルチデータ(SPMD)は、単一のプログラム(同一コード)がデバイス間で同時に実行される並行プログラミングモデルですが、実行中の各プログラムへの入力は異なる場合があります。
プログラムが入力の単純な関数である場合(x + 5 など)、SPMD でプログラムを実行すると、前に jax.pmap で行ったように、プログラムをさまざまなデータにマッピングするだけです。 ただし、関数を単に「マップ」するだけでなく、JAX は、デバイス間で通信する関数である「集合」を提供します。
たとえば、すべてのデバイスの数量の合計を取得する場合、 まず pmapでマッピングする軸に名前を割り当てる必要があります。次に、lax.psum ( 「parallel sum」)関数を使用してデバイス間で合計を実行し、合計する名前付き軸を確実に識別します。
def f(x):
out = lax.psum(x, axis_name='i')
return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)
ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)
psum 集合は、各デバイスの x の値を集約し、その値をマップ全体で同期します。つまり、out は各デバイスで 28. です。単純な「マップ」ではなく、SPMD プログラムを実行しています。SPMD プログラムでは、集合体を使用する方法は限られていますが、各デバイスの計算が他のデバイスの同じ計算と相互作用できるようになります。このシナリオでは、psum が値を同期するため、out_axes = None を使用できます。
def f(x):
out = lax.psum(x, axis_name='i')
return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))
ShardedDeviceArray(28., dtype=float32)
SPMD を使用すると、任意の TPU 構成のすべてのデバイスで同時に実行される 1 つのプログラムを作成できます。8 つの TPU コアで機械学習を行うために使用するコードを、数百から数千のコアを持つ TPU ポッドで使用できます。jax.pmap と SPMD の詳細なチュートリアルについては、JAX 101 チュートリアルを参照してください。
大規模な MCMC
このノートブックでは、ベイズ推定にマルコフ連鎖モンテカルロ(MCMC)法を使用することに焦点を当てています。MCMC に多くのデバイスを利用する方法はいくつかありますが、このノートブックでは、次の 2 つに焦点を当てます。
- 異なるデバイスで独立したマルコフ連鎖を実行します。このケースは非常に単純で、バニラ TFP で行うことができます。
- デバイス間でデータセットをシャーディングします。このケースはもう少し複雑で、最近追加された TFP 機能が必要です。
独立した連鎖
MCMC を使用して問題についてベイズ推定を行い、複数のデバイス間で複数のチェーンを並列に実行したいとします(たとえば、各デバイスで 2 つ)。これは、デバイス間で「マッピング」できるプログラム、つまり集合体を必要としないプログラムです。各プログラムが(同じマルコフ連鎖を実行するのではなく)異なるマルコフ連鎖を実行することを確認するために、各デバイスに異なる値のランダムシードを渡します。
2 次元ガウス分布からサンプリングするトイプロブレムで試してみましょう。TFP の既存の MCMC 機能をそのまま使用できます。一般に、マップされた関数内にほとんどのロジックを配置して、すべてのデバイスで実行されているものと最初のデバイスだけで実行されているものをより明確に区別します。
def run(seed):
target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob
initial_state = jnp.zeros([2, 2]) # 2 chains
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
def trace_fn(state, pkr):
return target_log_prob(state)
states, log_prob = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
kernel=kernel,
current_state=initial_state,
trace_fn=trace_fn,
seed=seed
)
return states, log_prob
run 関数は、それ自体でステートレスランダムシードを取り込みます(ステートレスランダム性がどのように機能するかを確認するには、 JAX で TFP を使用する ノートブック および JAX 101 チュートリアルを参照してください。異なるシードに run をマッピングすると、複数の独立したマルコフ連鎖が実行されます。
states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)
(8, 1000, 2, 2) (8, 1000, 2)
各デバイスに対応する追加の軸があることに注意してください。次元を並べ替えて平坦化し、16 の連鎖の軸を取得できます。
states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()
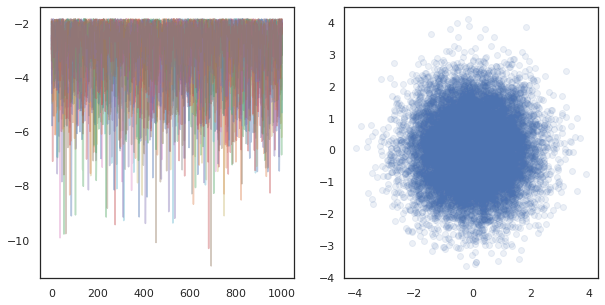
多くのデバイスで独立したチェーンを実行するのは、 tfp.mcmc を使用する関数で pmap を実行するだけで、各デバイスにランダムシードとして異なる値を渡すことができます。
データのシャーディング
MCMC では、多くの場合、ターゲットのディストリビューションはデータセットの条件付けによって取得された事後ディストリビューションであり、正規化されていない対数密度の計算には、観測された各データの尤度の合計が含まれます。
データセットが非常に大きい場合、1 台のデバイスで 1 つのチェーンを実行する場合にでも非常にコストがかかる可能性がありますが、複数のデバイスにアクセスできる場合は、データセットをデバイス間で分割して、利用可能なコンピューティングをより有効に活用できます。
シャーディングされたデータセットを使用して MCMC を実行する場合は、各デバイスで計算する非正規化対数密度が合計、つまりすべてのデータの密度を表すようにする必要があります。そうしないと、各デバイスは独自の誤ったターゲットディストリビューションで MCMC を実行します。そのため、TFP には、「シャーディングされた」対数確率の計算とそれらを使用した MCMC の実行を可能にする新しいツール(tfp.experimental.distribute と tfp.experimental.mcmc)があります。
シャーディングされたディストリビューション
TFP がシャーディングされた対数確率の計算に提供するコア抽象化は、Sharded メタディストリビューションです。これは、入力としてディストリビューションを受け取り、SPMD コンテキストで実行されると特定のプロパティを持つ新しいディストリビューションを返します。Sharded は tfp.experimental.distribute にあります。
直感的には、Sharded ディストリビューションは、デバイス間で「分割」された確率変数のセットに対応します。各デバイスで、それらは異なるサンプルを生成し、個別に異なる対数密度を持つことができます。あるいは、Sharded ディストリビューションは、グラフィカルモデル用語の「プレート」に対応します。プレートサイズはデバイス数です。
Sharded ディストリビューションのサンプリング
各デバイスで同じシードを使用してpmapを実行しているプログラムで、Normal ディストリビューションからサンプリングすると、各デバイスで同じサンプルが取得されます。次の関数は、デバイス間で同期される単一の確率変数をサンプリングするものと考えることができます。
# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32)
tfd.Normal(0., 1.) を tfed.Sharded でラップすると、論理的に 8 つの異なる確率変数(各デバイスに 1 つ)が存在するため、 同じシードを渡しても、それぞれに異なるサンプルを生成します。
def f(seed, _):
return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([ 1.2152631 , 0.7818249 , 0.32549605, 0.6828047 ,
1.3973192 , -0.57830244, 0.37862757, 2.7706041 ], dtype=float32)
単一のデバイスでのこの分布の同等の表現は、8 つの独立した正規サンプルです。サンプルの値は異なりますが (tfed.Sharded は疑似乱数の生成をわずかに異なる方法で行います。どちらも同じディストリビューションを表します。
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))
DeviceArray([ 0.08086783, -0.38624594, -0.3756545 , 1.668957 ,
-1.2758069 , 2.1192007 , -0.85821325, 1.1305912 ], dtype=float32)
Sharded ディストリビューションの対数密度を取得する
SPMD コンテキストで正規分布からサンプルの対数密度を計算するとどうなるか見てみましょう。
def f(seed, _):
dist = tfd.Normal(0., 1.)
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32),
ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
-0.94012403, -0.94012403, -0.94012403, -0.94012403], dtype=float32))
各サンプルは各デバイスで同じであるため、各デバイスで同じ密度を計算します。直感的には、ここでは、ディストリビューションは単一の正規分布変数にのみあります。
Sharded ディストリビューションでは、8 つの確率変数にわたるディストリビューションがあるため、サンプルのlog_prob を計算するときに、デバイス間で個々の対数密度をそれぞれ合計します。(この合計 log_prob 値は、上記で計算された単一の log_prob よりも大きいことに気付くかもしれません。)
def f(seed, _):
dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)
Sample: [ 1.2152631 0.7818249 0.32549605 0.6828047 1.3973192 -0.57830244 0.37862757 2.7706041 ] Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205]
同等の「シャーディングされていない」ディストリビューションは、同じ対数密度を生成します。
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)
DeviceArray(-13.7349205, dtype=float32)
Sharded ディストリビューションは、各デバイスの sample とは異なる値を生成しますが、各デバイスの log_prob に対して同じ値を取得します。何が起こっているのでしょうか? Sharded ディストリビューションは、psum を内部的に実行して、log_prob の値がデバイス間で同期していることを確認します。 なぜこの動作が必要なのでしょうか?各デバイスで 同じ MCMC チェーンを実行している場合、計算の確率変数がデバイス間でシャーディングされている場合でも、target_log_prob を各デバイスで同じにする必要があります。
さらに、Sharded ディストリビューションは、デバイス間の勾配が正しいことを保証し、遷移関数の一部として対数密度関数の勾配をとる HMC のようなアルゴリズムが適切なサンプルを生成することを保証します。
シャードされた JointDistribution
JointDistribution (JD)を使用して、複数の Sharded 確率変数を持つモデルを作成できます。残念ながら、Sharded ディストリビューションは、バニラ tfd.JointDistribution で安全に使用できませんが、tfp.experimental.distribute は、Sharded ディストリビューションのように動作する「パッチが適用された」JD をエクスポートします。
def f(seed, _):
dist = tfed.JointDistributionSequential([
tfd.Normal(0., 1.),
tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
])
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
1.6121525, 1.6121525, 1.6121525], dtype=float32),
ShardedDeviceArray([ 0.8690128 , -0.83167845, 1.2209264 , 0.88412696,
0.76478404, -0.66208494, -0.0129658 , 0.7391483 ], dtype=float32)],
ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
-12.214451, -12.214451, -12.214451, -12.214451], dtype=float32))
これらのシャーディングされた JD は、コンポーネントとして Sharded とバニラ TFP 分布の両方を持つことができます。シャーディングされていないディストリビューションの場合、各デバイスで同じサンプルを取得し、シャーディングされた分布の場合、異なるサンプルを取得します。各デバイスの log_prob も同期されます。
MCMC での Sharded ディストリビューション
MCMC のコンテキストでは、Sharded ディストリビューションについてどのように考えればよいでしょうか?JointDistribution として表現できる生成モデルがある場合、そのモデルの軸を選択して「シャーディング」することができます。通常、モデル内の 1 つの確率変数は観測データに対応し、デバイス間でシャーディングする大きなデータセットがある場合は、データポイントに関連付けられている変数もシャーディングする必要があります。また、シャーディングしている観測値と 1 対 1 の「ローカル」確率変数がある可能性があるため、これらの確率変数をさらにシャーディングする必要があります。
このセクションでは、TFP MCMC での Sharded ディストリビューションの使用例について説明します。 distribute ライブラリのいくつかのユースケースを示すために、単純なベイズロジスティック回帰の例と行列因数分解の例を見ていきます。
例: MNIST に対するベイズロジスティック回帰
大規模なデータセットに対してベイズロジスティック回帰を実行します。モデルには、回帰の重みよりも前の \(p(\theta)\) があり、 合計同時対数密度を取得するためのすべてのデータ \({x_i, y_i}_{i = 1}^N\) で合計される尤度 \(p(y_i | \theta, x_i)\) があります。データをシャーディングする場合、モデルで観測された確率変数 \(x_i\) と \(y_i\) をシャーディングします。
MNIST の分類には次のベイズロジスティック回帰モデルを使用します。\( \begin{align*} w &\sim \mathcal{N}(0, 1) \ b &\sim \mathcal{N}(0, 1) \ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \)
TensorFlow データセットを使用して MNIST を読み込みましょう。
mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.
raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.
Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1... WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your local data directory. If you'd instead prefer to read directly from our public GCS bucket (recommended if you're running on GCP), you can instead pass `try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`. HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio… Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.
60000 のトレーニング画像がありますが、利用可能な 8 つのコアを利用して、8 つの方法で分割します。次の便利な shard ユーティリティ関数を使用します。
def shard_value(x):
x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices
shard = functools.partial(jax.tree.map, shard_value)
sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)
(8, 7500, 784) (8, 7500)
先に進む前に、TPU の精度と HMC への影響について簡単に説明しましょう。TPUは、速度のために低い bfloat16 精度を使用して行列の乗算を実行します。bfloat16 行列の乗算は、頻繁に多くの深層学習アプリケーションに対して十分ですが、HMC で使用すると、精度が低いと軌道が発散し、拒否が発生する可能性があることが経験的に明らかになっています。追加の計算をいくらか犠牲にして、より高精度の行列乗算を使用できます。
matmul の精度を上げるには、"tensorfloat32" の精度で jax.default_matmul_precision デコレータを使用します(さらに精度を上げるには、"float32" の精度を使用できます。)
次に、run 関数を定義します。この関数は、ランダムシード(各デバイスで同じになります)と MNIST のシャードを取り込みます。この関数は前述のモデルを実装し、TFP のバニラ MCMC 機能を使用して単一のチェーンを実行します。run に jax.default_matmul_precision デコレータを使用して、行列の乗算がより高い精度で実行されるようにします。ただし、以下の特定の例では、jnp.dot(images, w, precision=lax.Precision.HIGH) を使用することもできます。
# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device.
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
images, labels = data # a sharded dataset
num_examples, dim = images.shape
num_classes = 10
def model_fn():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
logits = jnp.dot(images, w) + b
yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
shard_axis_name='data')
model = tfed.JointDistributionCoroutine(model_fn)
init_seed, sample_seed = random.split(seed)
initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`
def target_log_prob(*state):
return model.log_prob((*state, labels))
def accuracy(w, b):
logits = images.dot(w) + b
preds = logits.argmax(axis=-1)
# We take the average accuracy across devices by using `lax.pmean`
return lax.pmean((preds == labels).mean(), 'data')
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
def trace_fn(state, pkr):
return (
target_log_prob(*state),
accuracy(*state),
pkr.new_step_size)
states, trace = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
current_state=initial_state,
kernel=kernel,
trace_fn=trace_fn,
seed=sample_seed
)
return states, trace
jax.pmap には JIT コンパイルが含まれていますが、コンパイルされた関数は最初の呼び出し後にキャッシュされます。 run を呼び出し、出力を無視してコンパイルをキャッシュします。
%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree.map(lambda x: x.block_until_ready(), output)
CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s Wall time: 1min 54s
run を再度呼び出して、実際の実行にかかる時間を確認します。
%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree.map(lambda x: x.block_until_ready(), trace)
CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s Wall time: 1min 43s
200,000 のリープフロッグステップを実行しています。各ステップは、データセット全体の勾配を計算します。計算を 8 コアに分割すると、約 95 秒で 200,000 エポックのトレーニングに相当する計算が可能になります。これは 1 秒あたり約 2,100 エポックです。
各サンプルの対数密度と各サンプルの精度をプロットしてみましょう。
fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()
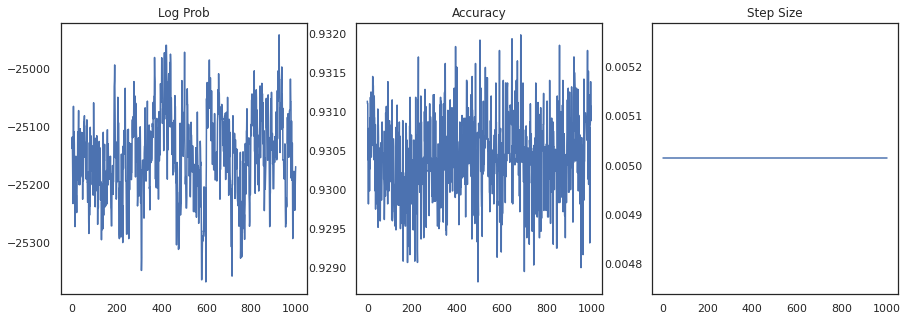
サンプルをアンサンブルすると、ベイズモデル平均化を計算してパフォーマンスを向上させることができます。
@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
images, labels = data
logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
probs = jax.nn.softmax(logits, axis=-1)
bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')
sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')
Average Accuracy: 0.9188529253005981 BMA Accuracy: 0.9264000058174133 Accuracy Improvement: 0.0075470805168151855
ベイズモデル平均化により、精度がほぼ 1 %向上します。
例: MovieLens 推奨システム
次に、ユーザーによる映画の評価が含まれた、MovieLens 推奨データセットを使用して推論を試してみます。具体的には、MovieLens を \(N \times M\) watch matrix \(W\) として表すことができます。ここで、\(N\) はユーザー数、\(M\) は映画数です。 \(N > M\) を期待します。\(W_{ij}\) のエントリは、ユーザー \(i\) が映画 \(j\) を視聴したかどうかを示すブール値です。MovieLens はユーザー評価を提供しますが、問題を単純化するためにそれらを無視していることに注意してください。
まず、データセットを読み込みます。100 万の評価があるバージョンを使用します。
movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']
Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0... HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl… HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value=''))) Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value=''))) Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.
データセットの前処理を行って、視聴行列 \(W\) を取得します。
raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']
movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])
num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1
movie_titles = dict(zip(movielens['train']['movie_id'],
movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]
watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)
(6040, 3706)
単純な確率的行列因数分解モデルを使用して、\(W\) の生成モデルを定義します。潜在的な \(N \times D\) ユーザー行列 \(U\) と潜在的な \(M \times D\) を想定します。これらを乗算すると、視聴行列 \(W\) のベルヌーイのロジットが生成されます。また、ユーザーと映画のバイアスベクトル、\(u\) と \(v\) も含まれます。\( \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \)
これはかなり大きな行列です。6040 のユーザーと 3706 の映画は、2,200 万を超えるエントリを含む行列につながります。このモデルのシャーディングにどのようにアプローチすればよいでしょうか。\(N > M\)(つまり、映画よりもユーザーが多い)と仮定すると、ユーザー軸全体で視聴行列をシャーディングするのが理にかなっているため、各デバイスにはサブセットに対応する視聴行列のチャンクがあります。ただし、前の例とは異なり、\(U\) 行列もシャーディングする必要があります。これは、ユーザーごとに埋め込みがあるため、各デバイスが \(U\) のシャードと \(W\) をシャーディングするためです。 一方、\(V\) はシャーディングされず、デバイス間で同期されます。
sharded_watch_matrix = shard(watch_matrix)
run を作成する前に、ローカル確率変数 \(U\) をシャーディングする際の追加の課題について簡単に説明します。HMC を実行している場合、バニラ tfp.mcmc.HamiltonianMonteCarlo カーネルは、チェーンの状態の各要素の運動量のサンプリングを実行します。以前は、シャーディングされていない確率変数のみがその状態の一部であり、運動量は各デバイスで同じでした。\(U\) がシャーディングされたら、\(V\) で同じ運動量をサンプリングしながら、各デバイスで \(U\) で異なる運動量をサンプリングする必要があります。そのためには、 tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo と Sharded 運動量ディストリビューションを使用できます。 並列計算をファーストクラスにし続けると、これを単純化することができます。つまり、HMC カーネルにシャードネスインジケーターを含めます。
def make_run(*,
axis_name,
dim=20,
num_chains=2,
prior_variance=1.,
step_size=1e-2,
num_leapfrog_steps=100,
num_burnin_steps=1000,
num_results=500,
):
@functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
@jax.default_matmul_precision('tensorfloat32')
def run(key, watch_matrix):
num_users, num_movies = watch_matrix.shape
Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)
def prior_fn():
user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
return (user_embeddings, user_bias, movie_embeddings, movie_bias)
prior = tfed.JointDistributionCoroutine(prior_fn)
def model_fn():
user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
+ user_bias[..., :, None] + movie_bias[..., None, :])
yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
model = tfed.JointDistributionCoroutine(model_fn)
init_key, sample_key = random.split(key)
initial_state = prior.sample(seed=init_key, sample_shape=num_chains)
def target_log_prob(*state):
return model.log_prob((*state, watch_matrix))
momentum_distribution = tfed.JointDistributionSequential([
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
])
# We pass in momentum_distribution here to ensure that the momenta for
# user_embeddings and user_bias are also sharded
kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
num_leapfrog_steps,
momentum_distribution=momentum_distribution)
num_adaptation_steps = int(0.8 * num_burnin_steps)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)
def trace_fn(state, pkr):
return {
'log_prob': target_log_prob(*state),
'log_accept_ratio': pkr.inner_results.log_accept_ratio,
}
return tfm.sample_chain(
num_results, initial_state,
kernel=kernel,
num_burnin_steps=num_burnin_steps,
trace_fn=trace_fn,
seed=sample_key)
return run
コンパイルされた run をキャッシュするために、もう 1 回実行します。
%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree.map(lambda x: x.block_until_ready(), output)
CPU times: user 56 s, sys: 1min 24s, total: 2min 20s Wall time: 3min 35s
次に、コンパイルのオーバーヘッドなしで再度実行します。
%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree.map(lambda x: x.block_until_ready(), trace)
CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s Wall time: 3min 1s
約 3 分で約 150,000 のリープフロッグステップを完了しました。つまり、1 秒あたり約 83 のリープフロッグステップです。サンプルの受け入れ率と対数密度をプロットします。
fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
ax.plot(val[0]) # Indexing into a sharded array, each element is the same
ax.set_title(key);
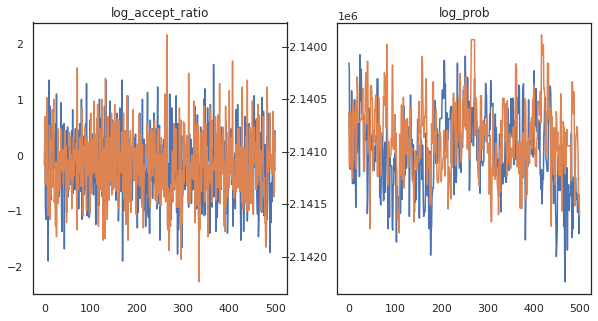
マルコフ連鎖のサンプルがいくつかあるので、それらを使用していくつかの予測を行います。まず、各コンポーネントを抽出します。user_embeddings と user_bias はデバイス間で分割されるため、ShardedArray を連結してすべてを取得する必要があることに注意してください。一方、movie_embeddings と movie_bias はすべてのデバイスで同じであるため、最初のシャードから値を選択するだけです。 通常の numpy を使用して、TPU から CPU に値をコピーします。
user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')
User embeddings: (500, 2, 6040, 20) User bias: (500, 2, 6040) Movie embeddings: (500, 2, 3706, 20) Movie bias: (500, 2, 3706)
これらのサンプルでキャプチャされた不確実性を利用する単純な推薦システムを構築してみましょう。まず、視聴確率に応じて映画をランク付けする関数を作成します。
@jax.jit
def recommend(sample, user_id):
user_embeddings, user_bias, movie_embeddings, movie_bias = sample
movie_logits = (
jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
+ user_bias[user_id] + movie_bias)
return movie_logits.argsort()[::-1]
これで、すべてのサンプルをループし、各サンプルについて、ユーザーがまだ視聴していない上位の映画を選択する関数を作成できます。 次に、サンプル全体で推奨されるすべての映画の数を確認できます。
def get_recommendations(user_id):
movie_ids = []
already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
for i in range(500):
for j in range(2):
sample = jax.tree.map(lambda x: x[i, j], samples)
ranking = recommend(sample, user_id)
for movie_id in ranking:
if int(movie_id) not in already_watched:
movie_ids.append(movie_id)
break
return movie_ids
def plot_recommendations(movie_ids, ax=None):
titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
ax = ax or plt.gca()
names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
ax.bar(names, counts)
ax.set_xticklabels(names, rotation=90)
映画の視聴数が最も多いユーザーと最も少ないユーザーを比較します。
user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])
2314 20
user_most が視聴する可能性が高い映画の種類に関する情報が多いので、システムは user_leastよりも user_most についてより確実であるはずです。
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');
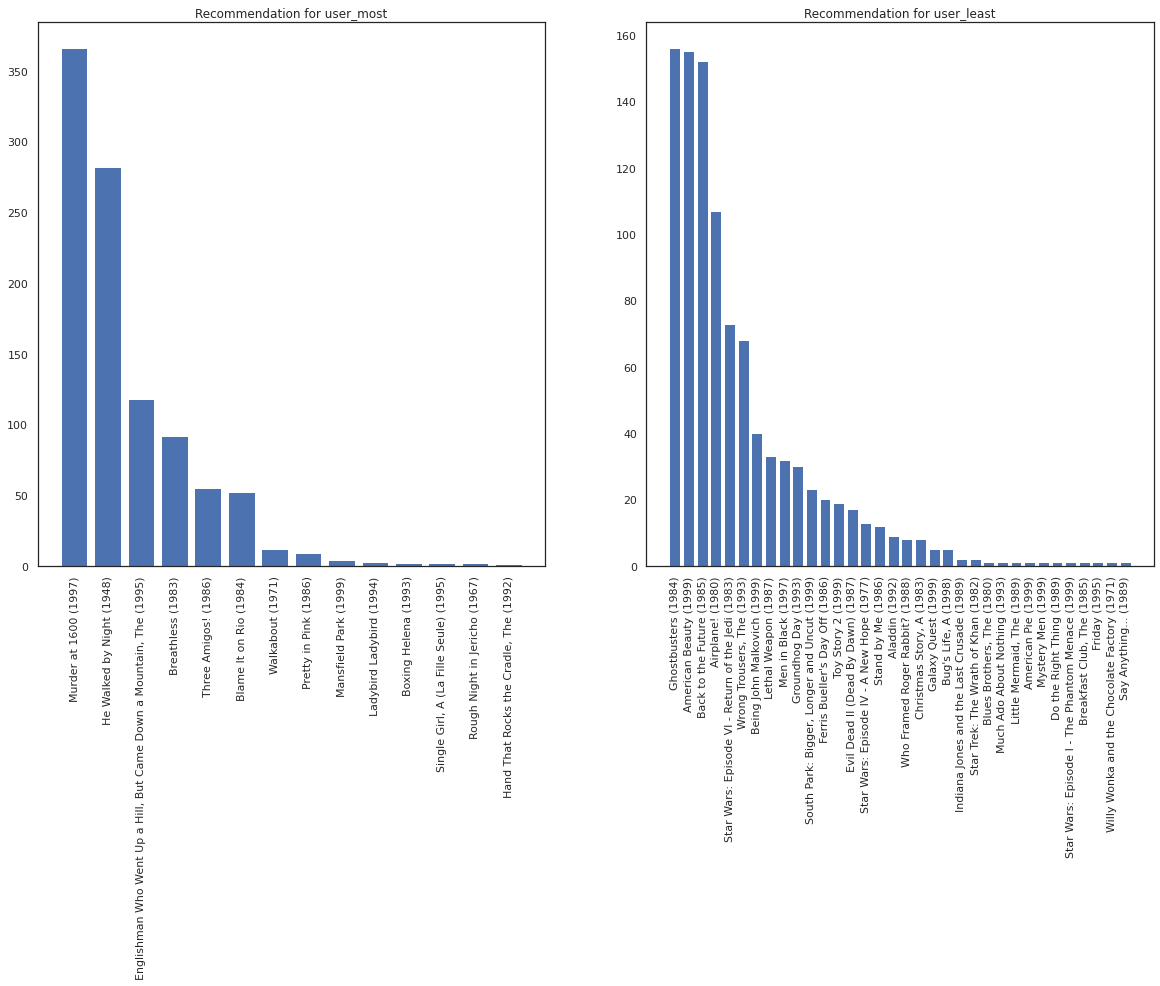
user_least の推奨事項には、視聴の好みにおける追加的な不確実性を反映され、より多くの差異があることがわかります。
また、推薦される映画のジャンルも見てみます。
most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');
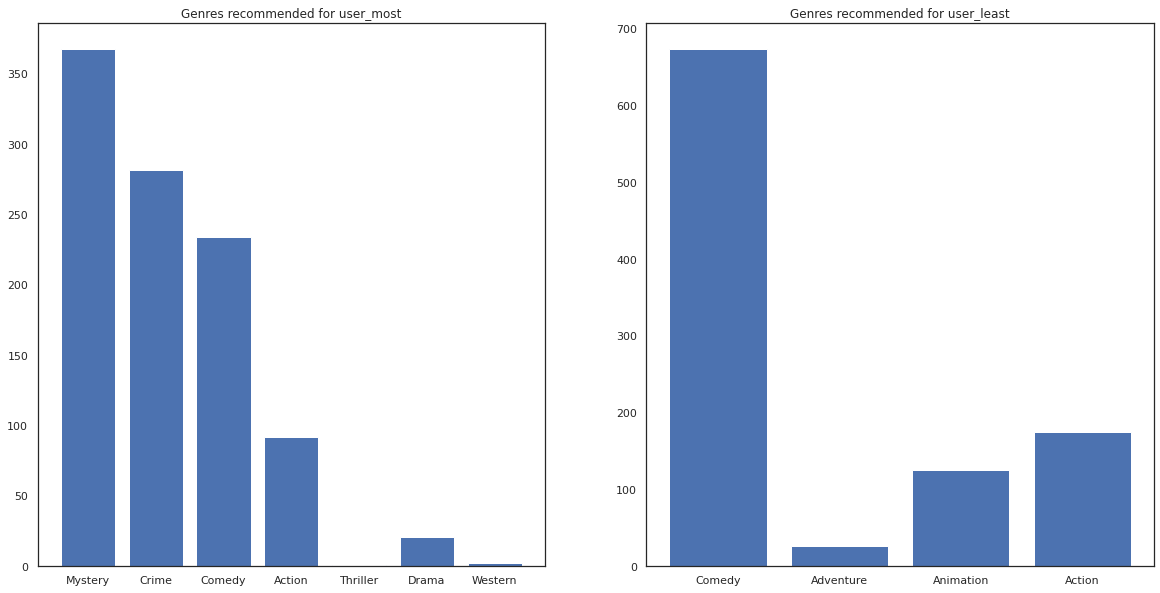
user_most は多くの映画を視聴しているので、ミステリーや犯罪などのよりニッチなジャンルが推奨されていますが、user_least は多くの映画を視聴していないので、コメディやアクションの主流の映画が推奨されています。
