 TensorFlow.org पर देखें TensorFlow.org पर देखें |  Google Colab में चलाएं Google Colab में चलाएं |  GitHub पर स्रोत देखें GitHub पर स्रोत देखें |  नोटबुक डाउनलोड करें नोटबुक डाउनलोड करें |
इस उदाहरण में हम दिखाते हैं कि TFP की "संभाव्य परतों" का उपयोग करके प्रतिगमन मॉडल को कैसे फिट किया जाए।
निर्भरता और पूर्वापेक्षाएँ
आयात
from pprint import pprint
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
sns.reset_defaults()
#sns.set_style('whitegrid')
#sns.set_context('talk')
sns.set_context(context='talk',font_scale=0.7)
%matplotlib inline
tfd = tfp.distributions
चीजें तेजी से करें!
इससे पहले कि हम इसमें गोता लगाएँ, आइए सुनिश्चित करें कि हम इस डेमो के लिए GPU का उपयोग कर रहे हैं।
ऐसा करने के लिए, "रनटाइम" -> "रनटाइम प्रकार बदलें" -> "हार्डवेयर त्वरक" -> "जीपीयू" चुनें।
निम्नलिखित स्निपेट सत्यापित करेगा कि हमारे पास GPU तक पहुंच है।
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
WARNING: GPU device not found.
प्रेरणा
क्या यह बहुत अच्छा नहीं होगा यदि हम एक संभाव्य मॉडल को निर्दिष्ट करने के लिए TFP का उपयोग कर सकते हैं, तो बस नकारात्मक लॉग-संभावना को कम करें, अर्थात,
negloglik = lambda y, rv_y: -rv_y.log_prob(y)
वैसे यह न सिर्फ संभव है, बल्कि यह कोलाब दिखाता है कि कैसे! (रैखिक प्रतिगमन समस्याओं के संदर्भ में।)
डेटासेट का संश्लेषण करें।
w0 = 0.125
b0 = 5.
x_range = [-20, 60]
def load_dataset(n=150, n_tst=150):
np.random.seed(43)
def s(x):
g = (x - x_range[0]) / (x_range[1] - x_range[0])
return 3 * (0.25 + g**2.)
x = (x_range[1] - x_range[0]) * np.random.rand(n) + x_range[0]
eps = np.random.randn(n) * s(x)
y = (w0 * x * (1. + np.sin(x)) + b0) + eps
x = x[..., np.newaxis]
x_tst = np.linspace(*x_range, num=n_tst).astype(np.float32)
x_tst = x_tst[..., np.newaxis]
return y, x, x_tst
y, x, x_tst = load_dataset()
केस 1: कोई अनिश्चितता नहीं
# Build model.
model = tf.keras.Sequential([
tf.keras.layers.Dense(1),
tfp.layers.DistributionLambda(lambda t: tfd.Normal(loc=t, scale=1)),
])
# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=negloglik)
model.fit(x, y, epochs=1000, verbose=False);
# Profit.
[print(np.squeeze(w.numpy())) for w in model.weights];
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
0.13032457 5.13029
चित्र 1: कोई अनिश्चितता नहीं।
w = np.squeeze(model.layers[-2].kernel.numpy())
b = np.squeeze(model.layers[-2].bias.numpy())
plt.figure(figsize=[6, 1.5]) # inches
#plt.figure(figsize=[8, 5]) # inches
plt.plot(x, y, 'b.', label='observed');
plt.plot(x_tst, yhat.mean(),'r', label='mean', linewidth=4);
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig1.png', bbox_inches='tight', dpi=300)
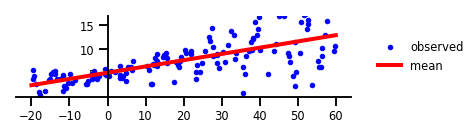
केस 2: एलेएटोरिक अनिश्चितता
# Build model.
model = tf.keras.Sequential([
tf.keras.layers.Dense(1 + 1),
tfp.layers.DistributionLambda(
lambda t: tfd.Normal(loc=t[..., :1],
scale=1e-3 + tf.math.softplus(0.05 * t[...,1:]))),
])
# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=negloglik)
model.fit(x, y, epochs=1000, verbose=False);
# Profit.
[print(np.squeeze(w.numpy())) for w in model.weights];
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
[0.14738432 0.1815331 ] [4.4812164 1.2219843]
चित्र 2: एलेएटोरिक अनिश्चितता
plt.figure(figsize=[6, 1.5]) # inches
plt.plot(x, y, 'b.', label='observed');
m = yhat.mean()
s = yhat.stddev()
plt.plot(x_tst, m, 'r', linewidth=4, label='mean');
plt.plot(x_tst, m + 2 * s, 'g', linewidth=2, label=r'mean + 2 stddev');
plt.plot(x_tst, m - 2 * s, 'g', linewidth=2, label=r'mean - 2 stddev');
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig2.png', bbox_inches='tight', dpi=300)
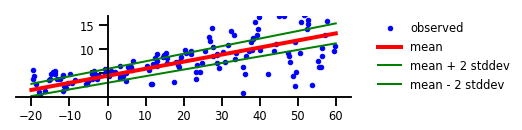
केस 3: महामारी संबंधी अनिश्चितता
# Specify the surrogate posterior over `keras.layers.Dense` `kernel` and `bias`.
def posterior_mean_field(kernel_size, bias_size=0, dtype=None):
n = kernel_size + bias_size
c = np.log(np.expm1(1.))
return tf.keras.Sequential([
tfp.layers.VariableLayer(2 * n, dtype=dtype),
tfp.layers.DistributionLambda(lambda t: tfd.Independent(
tfd.Normal(loc=t[..., :n],
scale=1e-5 + tf.nn.softplus(c + t[..., n:])),
reinterpreted_batch_ndims=1)),
])
# Specify the prior over `keras.layers.Dense` `kernel` and `bias`.
def prior_trainable(kernel_size, bias_size=0, dtype=None):
n = kernel_size + bias_size
return tf.keras.Sequential([
tfp.layers.VariableLayer(n, dtype=dtype),
tfp.layers.DistributionLambda(lambda t: tfd.Independent(
tfd.Normal(loc=t, scale=1),
reinterpreted_batch_ndims=1)),
])
# Build model.
model = tf.keras.Sequential([
tfp.layers.DenseVariational(1, posterior_mean_field, prior_trainable, kl_weight=1/x.shape[0]),
tfp.layers.DistributionLambda(lambda t: tfd.Normal(loc=t, scale=1)),
])
# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=negloglik)
model.fit(x, y, epochs=1000, verbose=False);
# Profit.
[print(np.squeeze(w.numpy())) for w in model.weights];
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
[ 0.1387333 5.125723 -4.112224 -2.2171402] [0.12476114 5.147452 ]
चित्र 3: महामारी संबंधी अनिश्चितता
plt.figure(figsize=[6, 1.5]) # inches
plt.clf();
plt.plot(x, y, 'b.', label='observed');
yhats = [model(x_tst) for _ in range(100)]
avgm = np.zeros_like(x_tst[..., 0])
for i, yhat in enumerate(yhats):
m = np.squeeze(yhat.mean())
s = np.squeeze(yhat.stddev())
if i < 25:
plt.plot(x_tst, m, 'r', label='ensemble means' if i == 0 else None, linewidth=0.5)
avgm += m
plt.plot(x_tst, avgm/len(yhats), 'r', label='overall mean', linewidth=4)
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig3.png', bbox_inches='tight', dpi=300)
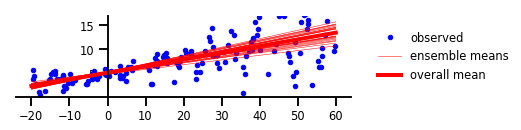
केस 4: एलिएटोरिक एंड एपिस्टेमिक अनिश्चितता
# Build model.
model = tf.keras.Sequential([
tfp.layers.DenseVariational(1 + 1, posterior_mean_field, prior_trainable, kl_weight=1/x.shape[0]),
tfp.layers.DistributionLambda(
lambda t: tfd.Normal(loc=t[..., :1],
scale=1e-3 + tf.math.softplus(0.01 * t[...,1:]))),
])
# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=negloglik)
model.fit(x, y, epochs=1000, verbose=False);
# Profit.
[print(np.squeeze(w.numpy())) for w in model.weights];
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
[ 0.12753433 2.7504077 5.160624 3.8251898 -3.4283297 -0.8961645 -2.2378397 0.1496858 ] [0.14511648 2.7104297 5.1248145 3.7724588 ]
चित्र 4: एलिएटोरिक और एपिस्टेमिक अनिश्चितता दोनों
plt.figure(figsize=[6, 1.5]) # inches
plt.plot(x, y, 'b.', label='observed');
yhats = [model(x_tst) for _ in range(100)]
avgm = np.zeros_like(x_tst[..., 0])
for i, yhat in enumerate(yhats):
m = np.squeeze(yhat.mean())
s = np.squeeze(yhat.stddev())
if i < 15:
plt.plot(x_tst, m, 'r', label='ensemble means' if i == 0 else None, linewidth=1.)
plt.plot(x_tst, m + 2 * s, 'g', linewidth=0.5, label='ensemble means + 2 ensemble stdev' if i == 0 else None);
plt.plot(x_tst, m - 2 * s, 'g', linewidth=0.5, label='ensemble means - 2 ensemble stdev' if i == 0 else None);
avgm += m
plt.plot(x_tst, avgm/len(yhats), 'r', label='overall mean', linewidth=4)
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig4.png', bbox_inches='tight', dpi=300)
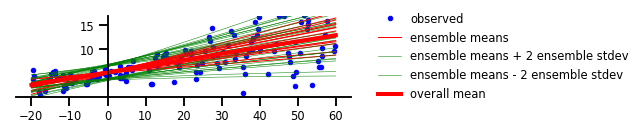
केस 5: कार्यात्मक अनिश्चितता
कस्टम PSD कर्नेल
class RBFKernelFn(tf.keras.layers.Layer):
def __init__(self, **kwargs):
super(RBFKernelFn, self).__init__(**kwargs)
dtype = kwargs.get('dtype', None)
self._amplitude = self.add_variable(
initializer=tf.constant_initializer(0),
dtype=dtype,
name='amplitude')
self._length_scale = self.add_variable(
initializer=tf.constant_initializer(0),
dtype=dtype,
name='length_scale')
def call(self, x):
# Never called -- this is just a layer so it can hold variables
# in a way Keras understands.
return x
@property
def kernel(self):
return tfp.math.psd_kernels.ExponentiatedQuadratic(
amplitude=tf.nn.softplus(0.1 * self._amplitude),
length_scale=tf.nn.softplus(5. * self._length_scale)
)
# For numeric stability, set the default floating-point dtype to float64
tf.keras.backend.set_floatx('float64')
# Build model.
num_inducing_points = 40
model = tf.keras.Sequential([
tf.keras.layers.InputLayer(input_shape=[1]),
tf.keras.layers.Dense(1, kernel_initializer='ones', use_bias=False),
tfp.layers.VariationalGaussianProcess(
num_inducing_points=num_inducing_points,
kernel_provider=RBFKernelFn(),
event_shape=[1],
inducing_index_points_initializer=tf.constant_initializer(
np.linspace(*x_range, num=num_inducing_points,
dtype=x.dtype)[..., np.newaxis]),
unconstrained_observation_noise_variance_initializer=(
tf.constant_initializer(np.array(0.54).astype(x.dtype))),
),
])
# Do inference.
batch_size = 32
loss = lambda y, rv_y: rv_y.variational_loss(
y, kl_weight=np.array(batch_size, x.dtype) / x.shape[0])
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=loss)
model.fit(x, y, batch_size=batch_size, epochs=1000, verbose=False)
# Profit.
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
चित्र 5: कार्यात्मक अनिश्चितता
y, x, _ = load_dataset()
plt.figure(figsize=[6, 1.5]) # inches
plt.plot(x, y, 'b.', label='observed');
num_samples = 7
for i in range(num_samples):
sample_ = yhat.sample().numpy()
plt.plot(x_tst,
sample_[..., 0].T,
'r',
linewidth=0.9,
label='ensemble means' if i == 0 else None);
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig5.png', bbox_inches='tight', dpi=300)

