 TensorFlow.orgで表示 |  GoogleColabで実行 |  GitHubでソースを表示 |  ノートブックをダウンロード |
このノートブックでは、TensorFlowディストリビューション（略してTFD）について説明します。このノートブックの目的は、TFDによるテンソル形状の処理を理解することを含め、学習曲線をゆっくりと上に上げることです。このノートブックは、抽象的な概念ではなく、前に例を提示しようとします。最初に物事を行うための標準的な簡単な方法を紹介し、最後まで最も一般的な抽象ビューを保存します。あなたはより抽象的かつ参照形式のチュートリアルを好むタイプなら、チェックアウトTensorFlow分布形状を理解します。あなたがここに材料についてのご質問がありましたら、連絡することを躊躇（または結合）していないTensorFlow確率メーリングリスト。喜んでお手伝いさせていただきます。
始める前に、適切なライブラリをインポートする必要があります。当社の全体的なライブラリがあるtensorflow_probability 。慣例により、我々は、一般的に分布ライブラリを参照してくださいtfd 。
TensorflowイーガーTensorFlowのための不可欠な実行環境です。 TensorFlow eagerでは、すべてのTF操作が即座に評価され、結果が生成されます。これは、TF操作が後で実行されるグラフにノードを追加するTensorFlowの標準の「グラフ」モードとは対照的です。このノートブック全体はTFEagerを使用して記述されていますが、ここで紹介する概念はいずれもそれに依存しておらず、TFPはグラフモードで使用できます。
import collections
import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions
try:
tf.compat.v1.enable_eager_execution()
except ValueError:
pass
import matplotlib.pyplot as plt
基本的な単変量分布
すぐに飛び込んで、正規分布を作成しましょう。
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
それからサンプルを引き出すことができます：
n.sample()
<tf.Tensor: shape=(), dtype=float32, numpy=0.25322816>
複数のサンプルを描画できます。
n.sample(3)
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.4658079, -0.5653636, 0.9314412], dtype=float32)>
対数確率を評価できます。
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
複数の対数確率を評価できます。
n.log_prob([0., 2., 4.])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-0.9189385, -2.9189386, -8.918939 ], dtype=float32)>
幅広いディストリビューションがあります。ベルヌーイを試してみましょう：
b = tfd.Bernoulli(probs=0.7)
b
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[] event_shape=[] dtype=int32>
b.sample()
<tf.Tensor: shape=(), dtype=int32, numpy=1>
b.sample(8)
<tf.Tensor: shape=(8,), dtype=int32, numpy=array([1, 0, 0, 0, 1, 0, 1, 0], dtype=int32)>
b.log_prob(1)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.35667497>
b.log_prob([1, 0, 1, 0])
<tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.35667497, -1.2039728 , -0.35667497, -1.2039728 ], dtype=float32)>
多変量分布
対角共分散を持つ多変量正規分布を作成します。
nd = tfd.MultivariateNormalDiag(loc=[0., 10.], scale_diag=[1., 4.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
これを以前に作成した単変量正規分布と比較すると、何が違うのでしょうか。
tfd.Normal(loc=0., scale=1.)
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
私たちは単変量通常は持っていることがわかりevent_shapeの() 、それはスカラー分布です示します。多変量正規が有するevent_shapeの2 、この分布の基本[イベントスペース（https://en.wikipedia.org/wiki/Event_（probability_theory））を示す、2次元です。
サンプリングは以前と同じように機能します。
nd.sample()
<tf.Tensor: shape=(2,), dtype=float32, numpy=array([-1.2489667, 15.025171 ], dtype=float32)>
nd.sample(5)
<tf.Tensor: shape=(5, 2), dtype=float32, numpy=
array([[-1.5439653 , 8.9968405 ],
[-0.38730723, 12.448896 ],
[-0.8697963 , 9.330035 ],
[-1.2541095 , 10.268944 ],
[ 2.3475595 , 13.184147 ]], dtype=float32)>
nd.log_prob([0., 10])
<tf.Tensor: shape=(), dtype=float32, numpy=-3.2241714>
多変量法線には、一般に対角共分散はありません。 TFDは、ここで使用する完全共分散仕様を含む、多変量法線を作成するための複数の方法を提供します。
nd = tfd.MultivariateNormalFullCovariance(
loc = [0., 5], covariance_matrix = [[1., .7], [.7, 1.]])
data = nd.sample(200)
plt.scatter(data[:, 0], data[:, 1], color='blue', alpha=0.4)
plt.axis([-5, 5, 0, 10])
plt.title("Data set")
plt.show()
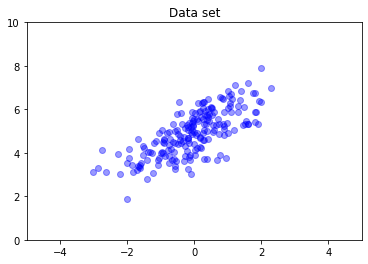
複数のディストリビューション
私たちの最初のベルヌーイ分布は、単一の公正なコインの裏返しを表しています。我々はまた、独立したベルヌーイ分布のバッチを作成することができ、自分のパラメータを持つそれぞれ、単一でDistribution対象：
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
これが何を意味するのかを明確にすることが重要です。上記の呼び出しは、同じPythonの中に含まれることが起こる三つの独立したベルヌーイ分布、定義Distributionオブジェクト。 3つの分布を個別に操作することはできません。どの音符batch_shapeある(3,) 、3つの分布のバッチを示し、そしてevent_shapeある()個々の分布は単変量イベントスペースを有する示します。
私たちが呼び出した場合sample 、我々はすべての3つのサンプルを取得します：
b3.sample()
<tf.Tensor: shape=(3,), dtype=int32, numpy=array([0, 1, 1], dtype=int32)>
b3.sample(6)
<tf.Tensor: shape=(6, 3), dtype=int32, numpy=
array([[1, 0, 1],
[0, 1, 1],
[0, 0, 1],
[0, 0, 1],
[0, 0, 1],
[0, 1, 0]], dtype=int32)>
我々が呼ぶ場合prob 、（これは同じ形状セマンティクス有するlog_prob 、我々が使用probが、明確にするためにこれらの小ベルヌーイ例とをlog_prob通常の用途において好ましい）、我々はベクトルを渡すことができ、その値を得た各硬貨の確率を評価します：
b3.prob([1, 1, 0])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.29999998], dtype=float32)>
APIにバッチ形状が含まれているのはなぜですか？意味的に、1は、ディストリビューションのリストを作成して、それらを反復処理することにより、同じ計算を行うことができfor （少なくともイーガーモードでは、TFグラフモードでは、あなたが必要があると思いループtf.whileループ）。ただし、同じようにパラメータ化された分布の（潜在的に大きな）セットを持つことは非常に一般的であり、可能な限りベクトル化された計算を使用することは、ハードウェアアクセラレータを使用して高速計算を実行できるようにするための重要な要素です。
独立を使用してバッチをイベントに集約する
前のセクションでは、我々が作成したb3 、単一のDistribution 3枚のコインが反転表現オブジェクト。私たちが呼び出された場合b3.prob 、ベクター上 \(v\)、 \(i\)番目のエントリは、確率だった \(i\)コイン番目の値がとる \(v[i]\)。
代わりに、同じ基礎となるファミリからの独立確率変数に対する「同時」分布を指定したいとします。このことは、この新たな分配のために、数学的に異なる目的であるprobベクターに \(v\) コインのセット全体は、ベクトルと一致する確率を表す単一の値が返されます \(v\)。
これをどのように達成しますか？私たちは、いわゆる「高次」ディストリビューションを使用Independentディストリビューションを取り、イベント形状に移動し、バッチ形状の新しい分布が得られ、：
b3_joint = tfd.Independent(b3, reinterpreted_batch_ndims=1)
b3_joint
<tfp.distributions.Independent 'IndependentBernoulli' batch_shape=[] event_shape=[3] dtype=int32>
オリジナルのものに形状を比較b3 ：
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
約束したように、我々はそのことを確認Independentイベント状に一括図形を移動した： b3_joint単一分布（あるbatch_shape = ()三次元のイベント空間上）（ event_shape = (3,)
セマンティクスを確認しましょう：
b3_joint.prob([1, 1, 0])
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999998>
同じ結果を得るための別の方法は、使用して計算確率になりb3と乗算する（または、対数確率が使用されるより一般的な場合には、加算）することにより、手動で還元を行います。
tf.reduce_prod(b3.prob([1, 1, 0]))
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999994>
Indpendent 、ユーザーがより明示的に必要な概念を表現することができます。厳密には必要ではありませんが、これは非常に便利であると考えています。
おもしろ情報：
-
b3.sampleとb3_joint.sample独立分布のバッチおよび使用バッチから作成された単一の分布の差：異なる概念の実装が、区別できない出力有するIndependentサンプリングする場合、コンピューティングprobabilitesアップショーをしません。 -
MultivariateNormalDiag自明スカラー使用して実装することができNormalとIndependent（それは実際にこのように実装されていませんが、それができる）分布を。
多変量分布のバッチ
3つの完全共分散2次元多変量法線のバッチを作成しましょう。
nd_batch = tfd.MultivariateNormalFullCovariance(
loc = [[0., 0.], [1., 1.], [2., 2.]],
covariance_matrix = [[[1., .1], [.1, 1.]],
[[1., .3], [.3, 1.]],
[[1., .5], [.5, 1.]]])
nd_batch
<tfp.distributions.MultivariateNormalFullCovariance 'MultivariateNormalFullCovariance' batch_shape=[3] event_shape=[2] dtype=float32>
我々は、参照batch_shape = (3,)ので、そこ三つの独立した多変量法線であり、そして、 event_shape = (2,)通常、各多変量は2次元であるので、。この例では、個々の分布に独立した要素はありません。
サンプリング作業：
nd_batch.sample(4)
<tf.Tensor: shape=(4, 3, 2), dtype=float32, numpy=
array([[[ 0.7367498 , 2.730996 ],
[-0.74080074, -0.36466932],
[ 0.6516018 , 0.9391426 ]],
[[ 1.038303 , 0.12231752],
[-0.94788766, -1.204232 ],
[ 4.059758 , 3.035752 ]],
[[ 0.56903946, -0.06875849],
[-0.35127294, 0.5311631 ],
[ 3.4635801 , 4.565582 ]],
[[-0.15989424, -0.25715637],
[ 0.87479895, 0.97391707],
[ 0.5211419 , 2.32108 ]]], dtype=float32)>
以降batch_shape = (3,)及びevent_shape = (2,)我々は、形状のテンソル通過(3, 2)をlog_prob 。
nd_batch.log_prob([[0., 0.], [1., 1.], [2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.8328519, -1.7907217, -1.694036 ], dtype=float32)>
放送、別名これはなぜそんなに混乱するのですか？
私たちがこれまで行ってきたのかを抽象化、すべてのディストリビューションは、バッチ形状ありBとイベント形状E 。してみましょうBEイベント形状の連結したもの：
- 一変量スカラー分布のために
n及びb、BE = ().。 - 二次元の多変量法線については
nd。BE = (2). - 両方のため
b3とb3_joint、BE = (3). - 多変量法線のバッチの
ndb、BE = (3, 2).
これまで使用してきた「評価ルール」は次のとおりです。
- 引数なしのサンプルは、形状とテンソルを返す
BE。スカラーnは戻って「nだけでサンプリングBE」テンソル。 -
probとlog_prob形状のテンソルが取るBEと形状の結果を返すB。
実際の「評価ルール」 probとlog_probより多くの方法で、複雑になる可能性の提供パワーとスピードだけでなく、複雑さと課題という。実際のルールは、引数こと（基本的に）であるlog_probなければなりませんbroadcastableに対するBE 。 「余分な」ディメンションはすべて出力に保持されます。
影響を調べてみましょう。一変量通常のためn 、 BE = ()ので、 log_probスカラーを期待。私たちが渡した場合log_prob空でない形状でテンソルを、それらが出力にバッチ寸法として表示します：
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
n.log_prob([0.])
<tf.Tensor: shape=(1,), dtype=float32, numpy=array([-0.9189385], dtype=float32)>
n.log_prob([[0., 1.], [-1., 2.]])
<tf.Tensor: shape=(2, 2), dtype=float32, numpy=
array([[-0.9189385, -1.4189385],
[-1.4189385, -2.9189386]], dtype=float32)>
二次元の多変量正規へレッツ・ターンnd （例示目的のために変更されたパラメータ）：
nd = tfd.MultivariateNormalDiag(loc=[0., 1.], scale_diag=[1., 1.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
log_prob 「を期待」形状の引数(2,)が、それは、この形状に対してそれが放送任意の引数を受け付けます。
nd.log_prob([0., 0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
しかし、私たちは「もっと」の例に渡し、そのすべてを評価することができますlog_prob一度にS」：
nd.log_prob([[0., 0.],
[1., 1.],
[2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
おそらくそれほど魅力的ではありませんが、イベントのディメンションでブロードキャストできます。
nd.log_prob([0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
nd.log_prob([[0.], [1.], [2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
この方法でのブロードキャストは、「可能な限りブロードキャストを有効にする」設計の結果です。この使用法はやや物議を醸すものであり、TFPの将来のバージョンで削除される可能性があります。
次に、3つのコインの例をもう一度見てみましょう。
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
ここでは、各コインは頭をアップする確率を表すために放送を使用することは、非常に直感的です。
b3.prob([1])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.7 ], dtype=float32)>
（この比較b3.prob([1., 1., 1.])我々が使用し、バックだろう、 b3導入されましたが。）
今、私たちが知っているしたいとし、各コインのために、確率は、コインが頭を起動し、確率はそれが尾をアップします。私たちは試してみることを想像することができます：
b3.log_prob([0, 1])
残念ながら、これにより、長くて読みにくいスタックトレースでエラーが発生します。 b3ありBE = (3)私たちが通過しなければならないので、 b3.probに対して何かbroadcastableを(3,) [0, 1]形状有し(2)ので、放送やエラーを生成しません。代わりに、次のように言う必要があります。
b3.prob([[0], [1]])
<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[0.7, 0.5, 0.3],
[0.3, 0.5, 0.7]], dtype=float32)>
どうして？ [[0], [1]]形状有し(2, 1)それが形状に対してブロードキャストするように、 (3)の放送形状にするために(2, 3)
ブロードキャストは非常に強力です。使用するメモリの量を桁違いに減らすことができ、ユーザーコードが短くなることがよくあります。ただし、でプログラミングするのは難しい場合があります。あなたが呼び出す場合log_probとエラーを取得し、放送への障害はほぼ常に問題となっています。
さらに進む
このチュートリアルでは、（うまくいけば）簡単な紹介を提供しました。さらに進むためのいくつかの指針：
-
event_shape、batch_shapeとsample_shape任意のランク（このチュートリアルでは、彼らは常にスカラまたはランク1のどちらかである）ことができます。これにより電力が増加しますが、特に放送が関係している場合は、プログラミングの問題が発生する可能性があります。形状操作に追加の深いダイビングについては、理解TensorFlow分布形状を。 - TFPは、として知られている強力な抽象含む
Bijectorsと併せて、TransformedDistribution、容易に既存の分布の可逆変換である新たな分布を作成するための柔軟な、組成方法をもたらすが。私たちは、このすぐ上のチュートリアルを書いてみるが、その間に、チェックアウトしますドキュメントを