Licensed under the MIT License
# Permission is hereby granted, free of charge, to any person obtaining a copy
# of this software and associated documentation files (the "Software"), to deal
# in the Software without restriction, including without limitation the rights
# to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
# copies of the Software, and to permit persons to whom the Software is
# furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in all
# copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
# AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
# OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
# SOFTWARE.
 TensorFlow.org で表示 TensorFlow.org で表示 |
 Google Colab で実行 Google Colab で実行 |
 GitHub でソースを表示 GitHub でソースを表示 |
 ノートブックをダウンロード ノートブックをダウンロード |
2020 年初期、COVID-19 の拡散速度を抑えるため、欧州諸国は、必要不可欠でない事業の営業休止、個々人の隔離、旅行禁止、ソーシャルディスタンスを促進するための対策といった医薬品に依存しない介入を適用しました。Imperial College COVID-19 Response Team が発表した「Estimating the number of infections and the impact of non-pharmaceutical interventions on COVID-19 in 11 European countries」という論文では、機構的な疫学モデルを合わせたベイズ階級モデルを使って、こういった対策の有効性が分析されています。
この Colab には、その分析の TensorFlow Probability(TFP)実装が含まれており、次のように構成されています。
- 「モデルのセットアップ」では、伝染とそれに起因する死亡数の疫学モデル、モデルパラメータに対するベイズ事前分布、およびパラメータ値を条件とする死亡数の分布を定義します。
- 「データの事前処理」では、各国の介入時期とその種類、経時的な死亡数、および感染者の推定致死率に関するデータを読み込みます。
- 「モデルの推論」では、パラメータに対する事後分布からサンプルを取得するために、ベイズ階級モデルを構築してハミルトニアンモンテカルロ(HMC)を実行します。
- 「結果」では、予想死亡数や介入がない場合の反事実的死亡数などの数量の事後予測分布を示します。
この論文では、感染者から感染した新たな感染者数(\(R_t\))を減少させることができたが、信頼区間には \(R_t=1\)(それを超えると感染が広がり続ける値)が含まれていたため、介入の有効性に関する確固たる結論を導き出すには時期尚早であることがわかりました。この論文の Stan コードは著者の Github リポジトリにあり、この Colab はバージョン 2を再現しています。
pip3 install -q git+git://github.com/arviz-devs/arviz.gitpip3 install -q tf-nightly tfp-nightly
Imports
import collections
from pprint import pprint
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability.python.internal import prefer_static as ps
tf.enable_v2_behavior()
# Globally Enable XLA.
# tf.config.optimizer.set_jit(True)
try:
physical_devices = tf.config.list_physical_devices('GPU')
tf.config.experimental.set_memory_growth(physical_devices[0], True)
except:
# Invalid device or cannot modify virtual devices once initialized.
pass
tfb = tfp.bijectors
tfd = tfp.distributions
DTYPE = np.float32
1. モデルのセットアップ
1.1 感染と死亡の機構的モデル
感染モデルは、各国の経時的な感染数をシミュレーションします。入力データは、介入、人口サイズ、初期事象のタイミングと種類です。パラメータは介入の有効性と伝播率を制御します。予測される死亡数のモデルは予測される感染に致死率を適用します。
この感染モデルは、発症間隔分布(感染から二次感染までの日数に対する分布)を使用して、以前の毎日の感染数の畳み込みを行います。時間ステップごとに、 \(t\), \(n_t\) 時点での新たな感染数が次のように計算されます。
\begin{equation} \sum_{i=0}^{t-1} n_i \mu_t \text{p} (\text{caught from someone infected at } i | \text{newly infected at } t) \end{equation} ここで、\(\mu_t=R_t\) であり、条件確率は、以下に定義されるように、conv_serial_interval に格納されます。
予想される死亡数のモデルは、毎日の感染数と感染から死亡までの日数の分布の畳み込みを実行します。つまり、\(t\) の日に予想される死亡は次のように計算されます。
\begin{equation} \sum_{i=0}^{t-1} n_i\text{p(death on day \(t\)|infection on day \(i\))} \end{equation} ここで、条件確率は、以下に定義されるように、conv_fatality_rate に格納されます。
from tensorflow_probability.python.internal import broadcast_util as bu
def predict_infections(
intervention_indicators, population, initial_cases, mu, alpha_hier,
conv_serial_interval, initial_days, total_days):
"""Predict the number of infections by forward-simulation.
Args:
intervention_indicators: Binary array of shape
`[num_countries, total_days, num_interventions]`, in which `1` indicates
the intervention is active in that country at that time and `0` indicates
otherwise.
population: Vector of length `num_countries`. Population of each country.
initial_cases: Array of shape `[batch_size, num_countries]`. Number of cases
in each country at the start of the simulation.
mu: Array of shape `[batch_size, num_countries]`. Initial reproduction rate
(R_0) by country.
alpha_hier: Array of shape `[batch_size, num_interventions]` representing
the effectiveness of interventions.
conv_serial_interval: Array of shape
`[total_days - initial_days, total_days]` output from
`make_conv_serial_interval`. Convolution kernel for serial interval
distribution.
initial_days: Integer, number of sequential days to seed infections after
the 10th death in a country. (N0 in the authors' Stan code.)
total_days: Integer, number of days of observed data plus days to forecast.
(N2 in the authors' Stan code.)
Returns:
predicted_infections: Array of shape
`[total_days, batch_size, num_countries]`. (Batched) predicted number of
infections over time and by country.
"""
alpha = alpha_hier - tf.cast(np.log(1.05) / 6.0, DTYPE)
# Multiply the effectiveness of each intervention in each country (alpha)
# by the indicator variable for whether the intervention was active and sum
# over interventions, yielding an array of shape
# [total_days, batch_size, num_countries] that represents the total effectiveness of
# all interventions in each country on each day (for a batch of data).
linear_prediction = tf.einsum(
'ijk,...k->j...i', intervention_indicators, alpha)
# Adjust the reproduction rate per country downward, according to the
# effectiveness of the interventions.
rt = mu * tf.exp(-linear_prediction, name='reproduction_rate')
# Initialize storage array for daily infections and seed it with initial
# cases.
daily_infections = tf.TensorArray(
dtype=DTYPE, size=total_days, element_shape=initial_cases.shape)
for i in range(initial_days):
daily_infections = daily_infections.write(i, initial_cases)
# Initialize cumulative cases.
init_cumulative_infections = initial_cases * initial_days
# Simulate forward for total_days days.
cond = lambda i, *_: i < total_days
def body(i, prev_daily_infections, prev_cumulative_infections):
# The probability distribution over days j that someone infected on day i
# caught the virus from someone infected on day j.
p_infected_on_day = tf.gather(
conv_serial_interval, i - initial_days, axis=0)
# Multiply p_infected_on_day by the number previous infections each day and
# by mu, and sum to obtain new infections on day i. Mu is adjusted by
# the fraction of the population already infected, so that the population
# size is the upper limit on the number of infections.
prev_daily_infections_array = prev_daily_infections.stack()
to_sum = prev_daily_infections_array * bu.left_justified_expand_dims_like(
p_infected_on_day, prev_daily_infections_array)
convolution = tf.reduce_sum(to_sum, axis=0)
rt_adj = (
(population - prev_cumulative_infections) / population
) * tf.gather(rt, i)
new_infections = rt_adj * convolution
# Update the prediction array and the cumulative number of infections.
daily_infections = prev_daily_infections.write(i, new_infections)
cumulative_infections = prev_cumulative_infections + new_infections
return i + 1, daily_infections, cumulative_infections
_, daily_infections_final, last_cumm_sum = tf.while_loop(
cond, body,
(initial_days, daily_infections, init_cumulative_infections),
maximum_iterations=(total_days - initial_days))
return daily_infections_final.stack()
def predict_deaths(predicted_infections, ifr_noise, conv_fatality_rate):
"""Expected number of reported deaths by country, by day.
Args:
predicted_infections: Array of shape
`[total_days, batch_size, num_countries]` output from
`predict_infections`.
ifr_noise: Array of shape `[batch_size, num_countries]`. Noise in Infection
Fatality Rate (IFR).
conv_fatality_rate: Array of shape
`[total_days - 1, total_days, num_countries]`. Convolutional kernel for
calculating fatalities, output from `make_conv_fatality_rate`.
Returns:
predicted_deaths: Array of shape `[total_days, batch_size, num_countries]`.
(Batched) predicted number of deaths over time and by country.
"""
# Multiply the number of infections on day j by the probability of death
# on day i given infection on day j, and sum over j. This yields the expected
result_remainder = tf.einsum(
'i...j,kij->k...j', predicted_infections, conv_fatality_rate) * ifr_noise
# Concatenate the result with a vector of zeros so that the first day is
# included.
result_temp = 1e-15 * predicted_infections[:1]
return tf.concat([result_temp, result_remainder], axis=0)
1.2 パラメータ値に対する事前確率
ここでは、モデルパラメータに対する同時事前分布を定義します。 パラメータ値の多くは独立していると想定されているため、事前値は次のように表すことができます。
\(\text p(\tau, y, \psi, \kappa, \mu, \alpha) = \text p(\tau)\text p(y|\tau)\text p(\psi)\text p(\kappa)\text p(\mu|\kappa)\text p(\alpha)\text p(\epsilon)\)
上記は、次を意味します。
- \(\tau\) は、国ごとの初期ケース数に対する指数分布の共有レートパラメータです(\(y = y_1, ... y_{\text{num_countries} }\))。
- \(\psi\) は、死亡数の負の二項分布のパラメータです。
- \(\kappa\) は、国ごとの初期再生産数に対する半正規分布の共有スケールパラメータで(\(\mu = \mu_1, ..., \mu_{\text{num_countries} }\))、各感染者が伝播した追加ケースの件数を示します。
- \(\alpha = \alpha_1, ..., \alpha_6\) は、各 6 個の介入の有効性です。
- \(\epsilon\)(作者の Stan コードにちなみ、コードでは
ifr_noiseと呼ばれる)は、感染致死率(IFR)内のノイズです。
このモデルを、確率的グラフィカルモデルの式を実現する TFP 分布の一種である TFP JointDistribution として表現します。
def make_jd_prior(num_countries, num_interventions):
return tfd.JointDistributionSequentialAutoBatched([
# Rate parameter for the distribution of initial cases (tau).
tfd.Exponential(rate=tf.cast(0.03, DTYPE)),
# Initial cases for each country.
lambda tau: tfd.Sample(
tfd.Exponential(rate=tf.cast(1, DTYPE) / tau),
sample_shape=num_countries),
# Parameter in Negative Binomial model for deaths (psi).
tfd.HalfNormal(scale=tf.cast(5, DTYPE)),
# Parameter in the distribution over the initial reproduction number, R_0
# (kappa).
tfd.HalfNormal(scale=tf.cast(0.5, DTYPE)),
# Initial reproduction number, R_0, for each country (mu).
lambda kappa: tfd.Sample(
tfd.TruncatedNormal(loc=3.28, scale=kappa, low=1e-5, high=1e5),
sample_shape=num_countries),
# Impact of interventions (alpha; shared for all countries).
tfd.Sample(
tfd.Gamma(tf.cast(0.1667, DTYPE), 1), sample_shape=num_interventions),
# Multiplicative noise in Infection Fatality Rate.
tfd.Sample(
tfd.TruncatedNormal(
loc=tf.cast(1., DTYPE), scale=0.1, low=1e-5, high=1e5),
sample_shape=num_countries)
])
1.3 パラメータ値を条件として観察された死亡数の尤度
この尤度モデルは、\(p(\text{deaths} | \tau, y, \psi, \kappa, \mu, \alpha, \epsilon)\) を表現します。これは、パラメータを条件として感染数と予想死亡数のモデルを適用し、実際の死亡は負の二項分布に従うと想定しています。
def make_likelihood_fn(
intervention_indicators, population, deaths,
infection_fatality_rate, initial_days, total_days):
# Create a mask for the initial days of simulated data, as they are not
# counted in the likelihood.
observed_deaths = tf.constant(deaths.T[np.newaxis, ...], dtype=DTYPE)
mask_temp = deaths != -1
mask_temp[:, :START_DAYS] = False
observed_deaths_mask = tf.constant(mask_temp.T[np.newaxis, ...])
conv_serial_interval = make_conv_serial_interval(initial_days, total_days)
conv_fatality_rate = make_conv_fatality_rate(
infection_fatality_rate, total_days)
def likelihood_fn(tau, initial_cases, psi, kappa, mu, alpha_hier, ifr_noise):
# Run models for infections and expected deaths
predicted_infections = predict_infections(
intervention_indicators, population, initial_cases, mu, alpha_hier,
conv_serial_interval, initial_days, total_days)
e_deaths_all_countries = predict_deaths(
predicted_infections, ifr_noise, conv_fatality_rate)
# Construct the Negative Binomial distribution for deaths by country.
mu_m = tf.transpose(e_deaths_all_countries, [1, 0, 2])
psi_m = psi[..., tf.newaxis, tf.newaxis]
probs = tf.clip_by_value(mu_m / (mu_m + psi_m), 1e-9, 1.)
likelihood_elementwise = tfd.NegativeBinomial(
total_count=psi_m, probs=probs).log_prob(observed_deaths)
return tf.reduce_sum(
tf.where(observed_deaths_mask,
likelihood_elementwise,
tf.zeros_like(likelihood_elementwise)),
axis=[-2, -1])
return likelihood_fn
1.4 感染した場合の死亡確率
このセクションは、感染後の日数における死亡数の分布を計算します。感染してから死亡するまでの時間は、感染から発症までの期間と発症から死亡までの期間を表す 2つのガンマ変量の量の合計であると想定しています。死亡までの期間の分布は、Verity et al. (2020) の感染致死率データと合わされて、感染後の日数における死亡確率の計算が行われます。
def daily_fatality_probability(infection_fatality_rate, total_days):
"""Computes the probability of death `d` days after infection."""
# Convert from alternative Gamma parametrization and construct distributions
# for number of days from infection to onset and onset to death.
concentration1 = tf.cast((1. / 0.86)**2, DTYPE)
rate1 = concentration1 / 5.1
concentration2 = tf.cast((1. / 0.45)**2, DTYPE)
rate2 = concentration2 / 18.8
infection_to_onset = tfd.Gamma(concentration=concentration1, rate=rate1)
onset_to_death = tfd.Gamma(concentration=concentration2, rate=rate2)
# Create empirical distribution for number of days from infection to death.
inf_to_death_dist = tfd.Empirical(
infection_to_onset.sample([5e6]) + onset_to_death.sample([5e6]))
# Subtract the CDF value at day i from the value at day i + 1 to compute the
# probability of death on day i given infection on day 0, and given that
# death (not recovery) is the outcome.
times = np.arange(total_days + 1., dtype=DTYPE) + 0.5
cdf = inf_to_death_dist.cdf(times).numpy()
f_before_ifr = cdf[1:] - cdf[:-1]
# Explicitly set the zeroth value to the empirical cdf at time 1.5, to include
# the mass between time 0 and time .5.
f_before_ifr[0] = cdf[1]
# Multiply the daily fatality rates conditional on infection and eventual
# death (f_before_ifr) by the infection fatality rates (probability of death
# given intection) to obtain the probability of death on day i conditional
# on infection on day 0.
return infection_fatality_rate[..., np.newaxis] * f_before_ifr
def make_conv_fatality_rate(infection_fatality_rate, total_days):
"""Computes the probability of death on day `i` given infection on day `j`."""
p_fatal_all_countries = daily_fatality_probability(
infection_fatality_rate, total_days)
# Use the probability of death d days after infection in each country
# to build an array of shape [total_days - 1, total_days, num_countries],
# where the element [i, j, c] is the probability of death on day i+1 given
# infection on day j in country c.
conv_fatality_rate = np.zeros(
[total_days - 1, total_days, p_fatal_all_countries.shape[0]])
for n in range(1, total_days):
conv_fatality_rate[n - 1, 0:n, :] = (
p_fatal_all_countries[:, n - 1::-1]).T
return tf.constant(conv_fatality_rate, dtype=DTYPE)
1.5 連続間隔
連続間隔は、一連の病気の伝染における連続した症例間の時間であり、ガンマ分布であると想定されます。連続間隔分布を使用して、\(i\) の日に感染した人が \(j\) の日にすでに感染していた人からウイルス感染した確率を計算します(predict_infections への conv_serial_interval 引数)。
def make_conv_serial_interval(initial_days, total_days):
"""Construct the convolutional kernel for infection timing."""
g = tfd.Gamma(tf.cast(1. / (0.62**2), DTYPE), 1./(6.5*0.62**2))
g_cdf = g.cdf(np.arange(total_days, dtype=DTYPE))
# Approximate the probability mass function for the number of days between
# successive infections.
serial_interval = g_cdf[1:] - g_cdf[:-1]
# `conv_serial_interval` is an array of shape
# [total_days - initial_days, total_days] in which entry [i, j] contains the
# probability that an individual infected on day i + initial_days caught the
# virus from someone infected on day j.
conv_serial_interval = np.zeros([total_days - initial_days, total_days])
for n in range(initial_days, total_days):
conv_serial_interval[n - initial_days, 0:n] = serial_interval[n - 1::-1]
return tf.constant(conv_serial_interval, dtype=DTYPE)
2 データの前処理
COUNTRIES = [
'Austria',
'Belgium',
'Denmark',
'France',
'Germany',
'Italy',
'Norway',
'Spain',
'Sweden',
'Switzerland',
'United_Kingdom'
]
2.1 Fetch and preprocess interventions data
raw_interventions = pd.read_csv(
'https://raw.githubusercontent.com/ImperialCollegeLondon/covid19model/master/data/interventions.csv')
raw_interventions['Date effective'] = pd.to_datetime(
raw_interventions['Date effective'], dayfirst=True)
interventions = raw_interventions.pivot(index='Country', columns='Type', values='Date effective')
# If any interventions happened after the lockdown, use the date of the lockdown.
for col in interventions.columns:
idx = interventions[col] > interventions['Lockdown']
interventions.loc[idx, col] = interventions[idx]['Lockdown']
num_countries = len(COUNTRIES)
2.2 Fetch case/death data and join to interventions
# Load the case data
data = pd.read_csv('https://raw.githubusercontent.com/ImperialCollegeLondon/covid19model/master/data/COVID-19-up-to-date.csv')
# You can also use the dataset directly from european cdc (where the ICL model fetch their data from)
# data = pd.read_csv('https://opendata.ecdc.europa.eu/covid19/casedistribution/csv')
data['country'] = data['countriesAndTerritories']
data = data[['dateRep', 'cases', 'deaths', 'country']]
data = data[data['country'].isin(COUNTRIES)]
data['dateRep'] = pd.to_datetime(data['dateRep'], format='%d/%m/%Y')
# Add 0/1 features for whether or not each intevention was in place.
data = data.join(interventions, on='country', how='outer')
for col in interventions.columns:
data[col] = (data['dateRep'] >= data[col]).astype(int)
# Add "any_intevention" 0/1 feature.
any_intervention_list = ['Schools + Universities',
'Self-isolating if ill',
'Public events',
'Lockdown',
'Social distancing encouraged']
data['any_intervention'] = (
data[any_intervention_list].apply(np.sum, 'columns') > 0).astype(int)
# Index by country and date.
data = data.sort_values(by=['country', 'dateRep'])
data = data.set_index(['country', 'dateRep'])
2.3 Fetch and process Infected Fatality Ratio and population data
infected_fatality_ratio = pd.read_csv(
'https://raw.githubusercontent.com/ImperialCollegeLondon/covid19model/master/data/popt_ifr.csv')
infected_fatality_ratio = infected_fatality_ratio.replace(to_replace='United Kingdom', value='United_Kingdom')
infected_fatality_ratio['Country'] = infected_fatality_ratio.iloc[:, 1]
infected_fatality_ratio = infected_fatality_ratio[infected_fatality_ratio['Country'].isin(COUNTRIES)]
infected_fatality_ratio = infected_fatality_ratio[
['Country', 'popt', 'ifr']].set_index('Country')
infected_fatality_ratio = infected_fatality_ratio.sort_index()
infection_fatality_rate = infected_fatality_ratio['ifr'].to_numpy()
population_value = infected_fatality_ratio['popt'].to_numpy()
2.4 国特有のデータを前処理する
# Model up to 75 days of data for each country, starting 30 days before the
# tenth cumulative death.
START_DAYS = 30
MAX_DAYS = 102
COVARIATE_COLUMNS = any_intervention_list + ['any_intervention']
# Initialize an array for number of deaths.
deaths = -np.ones((num_countries, MAX_DAYS), dtype=DTYPE)
# Assuming every intervention is still inplace in the unobserved future
num_interventions = len(COVARIATE_COLUMNS)
intervention_indicators = np.ones((num_countries, MAX_DAYS, num_interventions))
first_days = {}
for i, c in enumerate(COUNTRIES):
c_data = data.loc[c]
# Include data only after 10th death in a country.
mask = c_data['deaths'].cumsum() >= 10
# Get the date that the epidemic starts in a country.
first_day = c_data.index[mask][0] - pd.to_timedelta(START_DAYS, 'days')
c_data = c_data.truncate(before=first_day)
# Truncate the data after 28 March 2020 for comparison with Flaxman et al.
c_data = c_data.truncate(after='2020-03-28')
c_data = c_data.iloc[:MAX_DAYS]
days_of_data = c_data.shape[0]
deaths[i, :days_of_data] = c_data['deaths']
intervention_indicators[i, :days_of_data] = c_data[
COVARIATE_COLUMNS].to_numpy()
first_days[c] = first_day
# Number of sequential days to seed infections after the 10th death in a
# country. (N0 in authors' Stan code.)
INITIAL_DAYS = 6
# Number of days of observed data plus days to forecast. (N2 in authors' Stan
# code.)
TOTAL_DAYS = deaths.shape[1]
3 モデルの推論
Flaxman et al. (2020) は Stan を使用して、ハミルトニアンモンテカルロ(HMC)と No-U-Turn Sampler(NUTS)によるパラメータ事後分布からサンプルを取得しました。
ここでは、Dual-Averaging 法のステップサイズ適応で HMC を適用します。事前調整と初期化には、HMC のパイロットランを使用します。
推論は、GPU で数分間実行します。
3.1 モデルの事前分布と尤度を構築する
jd_prior = make_jd_prior(num_countries, num_interventions)
likelihood_fn = make_likelihood_fn(
intervention_indicators, population_value, deaths,
infection_fatality_rate, INITIAL_DAYS, TOTAL_DAYS)
3.2 ユーティリティ
def get_bijectors_from_samples(samples, unconstraining_bijectors, batch_axes):
"""Fit bijectors to the samples of a distribution.
This fits a diagonal covariance multivariate Gaussian transformed by the
`unconstraining_bijectors` to the provided samples. The resultant
transformation can be used to precondition MCMC and other inference methods.
"""
state_std = [
tf.math.reduce_std(bij.inverse(x), axis=batch_axes)
for x, bij in zip(samples, unconstraining_bijectors)
]
state_mu = [
tf.math.reduce_mean(bij.inverse(x), axis=batch_axes)
for x, bij in zip(samples, unconstraining_bijectors)
]
return [tfb.Chain([cb, tfb.Shift(sh), tfb.Scale(sc)])
for cb, sh, sc in zip(unconstraining_bijectors, state_mu, state_std)]
def generate_init_state_and_bijectors_from_prior(nchain, unconstraining_bijectors):
"""Creates an initial MCMC state, and bijectors from the prior."""
prior_samples = jd_prior.sample(4096)
bijectors = get_bijectors_from_samples(
prior_samples, unconstraining_bijectors, batch_axes=0)
init_state = [
bij(tf.zeros([nchain] + list(s), DTYPE))
for s, bij in zip(jd_prior.event_shape, bijectors)
]
return init_state, bijectors
@tf.function(autograph=False, experimental_compile=True)
def sample_hmc(
init_state,
step_size,
target_log_prob_fn,
unconstraining_bijectors,
num_steps=500,
burnin=50,
num_leapfrog_steps=10):
def trace_fn(_, pkr):
return {
'target_log_prob': pkr.inner_results.inner_results.accepted_results.target_log_prob,
'diverging': ~(pkr.inner_results.inner_results.log_accept_ratio > -1000.),
'is_accepted': pkr.inner_results.inner_results.is_accepted,
'step_size': [tf.exp(s) for s in pkr.log_averaging_step],
}
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn,
step_size=step_size,
num_leapfrog_steps=num_leapfrog_steps)
hmc = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc,
bijector=unconstraining_bijectors)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
hmc,
num_adaptation_steps=int(burnin * 0.8),
target_accept_prob=0.8,
decay_rate=0.5)
# Sampling from the chain.
return tfp.mcmc.sample_chain(
num_results=burnin + num_steps,
current_state=init_state,
kernel=hmc,
trace_fn=trace_fn)
3.3 事象空間バイジェクターを定義する
HMC は、等方的な多変量ガウス分布からサンプルを抽出する際に最も効率的である(Mangoubi & Smith (2017))ため、最初のステップは、ターゲット密度を調整してできる限りそのように見えるようにすることです。
まず初めに、制約付きの(非負など)変数を HMC が必要とする制約なしの空間に変換します。また、SinhArcsinh バイジェクターを使用して、変換されたターゲット密度のテールの重さを操作します。これらが、\(e^{-x^2}\) ほどに減少するよう目指します。
unconstraining_bijectors = [
tfb.Chain([tfb.Scale(tf.constant(1 / 0.03, DTYPE)), tfb.Softplus(),
tfb.SinhArcsinh(tailweight=tf.constant(1.85, DTYPE))]), # tau
tfb.Chain([tfb.Scale(tf.constant(1 / 0.03, DTYPE)), tfb.Softplus(),
tfb.SinhArcsinh(tailweight=tf.constant(1.85, DTYPE))]), # initial_cases
tfb.Softplus(), # psi
tfb.Softplus(), # kappa
tfb.Softplus(), # mu
tfb.Chain([tfb.Scale(tf.constant(0.4, DTYPE)), tfb.Softplus(),
tfb.SinhArcsinh(skewness=tf.constant(-0.2, DTYPE), tailweight=tf.constant(2., DTYPE))]), # alpha
tfb.Softplus(), # ifr_noise
]
3.4 HMC のパイロットラン
まず、事前分布で調整し、変換した空間で 0 から初期化される HMC を実行します。実際には事前分布のサンプルは、数値が不十分であるためにチェーンがスタックしてしまうことがよくあるため、チェーンの初期化に事前分布のサンプルは使用しません。
%%time
nchain = 32
target_log_prob_fn = lambda *x: jd_prior.log_prob(*x) + likelihood_fn(*x)
init_state, bijectors = generate_init_state_and_bijectors_from_prior(nchain, unconstraining_bijectors)
# Each chain gets its own step size.
step_size = [tf.fill([nchain] + [1] * (len(s.shape) - 1), tf.constant(0.01, DTYPE)) for s in init_state]
burnin = 200
num_steps = 100
pilot_samples, pilot_sampler_stat = sample_hmc(
init_state,
step_size,
target_log_prob_fn,
bijectors,
num_steps=num_steps,
burnin=burnin,
num_leapfrog_steps=10)
CPU times: user 56.8 s, sys: 2.34 s, total: 59.1 s Wall time: 1min 1s
3.5 パイロットサンプルを視覚化する
スタックしたチェーンを探し、収束に注目しています。ここでは正式な診断を行うことができますが、パイロットランであるため、絶対に必要と言うことではありません。
import arviz as az
az.style.use('arviz-darkgrid')
var_name = ['tau', 'initial_cases', 'psi', 'kappa', 'mu', 'alpha', 'ifr_noise']
pilot_with_warmup = {k: np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, pilot_samples)}
ウォームアップ中の発散を観察します。これは主に、Dual-Averaging のステップサイズ適応が非常に強引に最適なステップサイズを探すためです。適合がオフになると、発散もなくなります。
az_trace = az.from_dict(posterior=pilot_with_warmup,
sample_stats={'diverging': np.swapaxes(pilot_sampler_stat['diverging'].numpy(), 0, 1)})
az.plot_trace(az_trace, combined=True, compact=True, figsize=(12, 8));
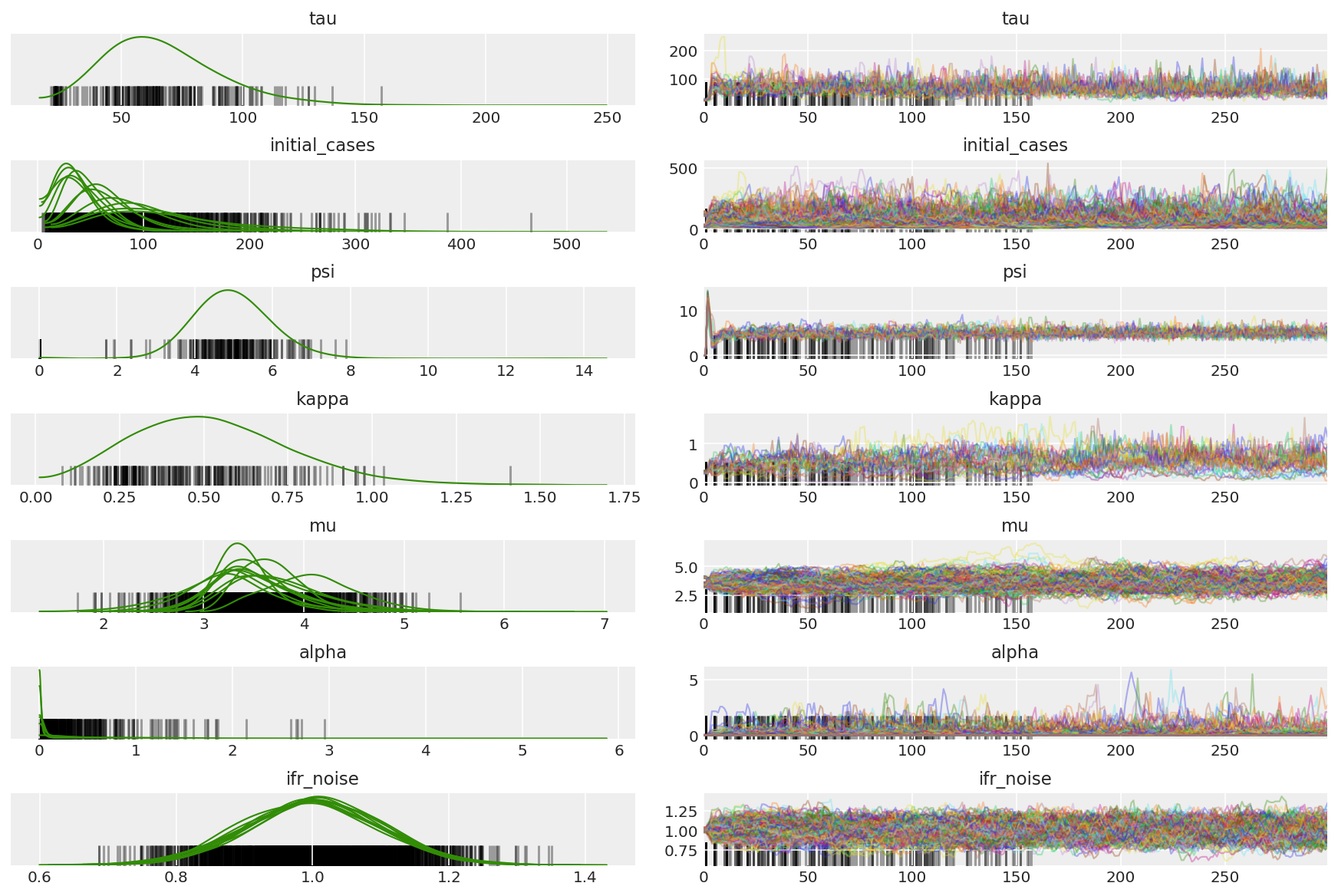
plt.plot(pilot_sampler_stat['step_size'][0]);
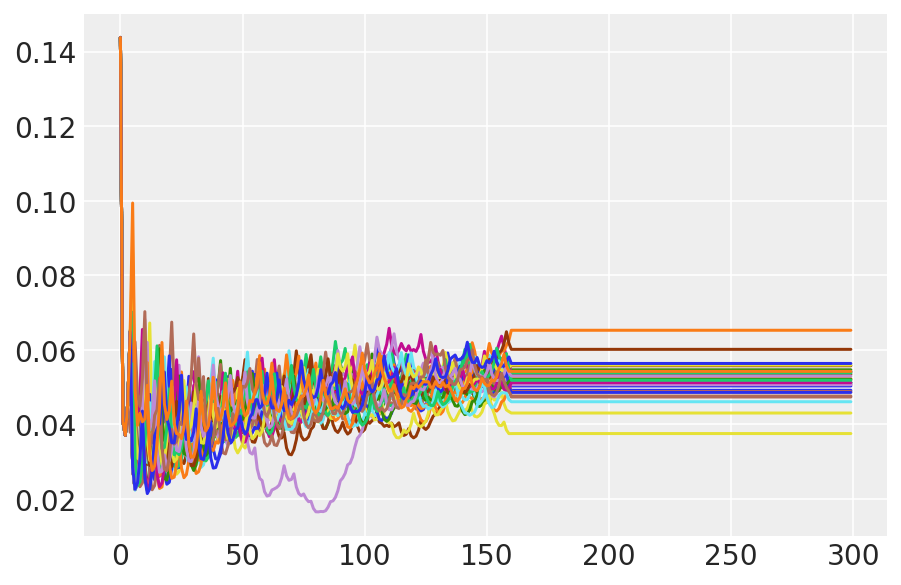
3.6 HMC を実行する
基本的に、最終的な分析にパイロットサンプルを使用することも可能です(収束を得るくらい長く実行した場合)が、別の HMC ランを開始する方が少しながらより効率的です。今回は、パイロットサンプルによって事前調整して初期化されたランを実行します。
%%time
burnin = 50
num_steps = 200
bijectors = get_bijectors_from_samples([s[burnin:] for s in pilot_samples],
unconstraining_bijectors=unconstraining_bijectors,
batch_axes=(0, 1))
samples, sampler_stat = sample_hmc(
[s[-1] for s in pilot_samples],
[s[-1] for s in pilot_sampler_stat['step_size']],
target_log_prob_fn,
bijectors,
num_steps=num_steps,
burnin=burnin,
num_leapfrog_steps=20)
CPU times: user 1min 26s, sys: 3.88 s, total: 1min 30s Wall time: 1min 32s
plt.plot(sampler_stat['step_size'][0]);
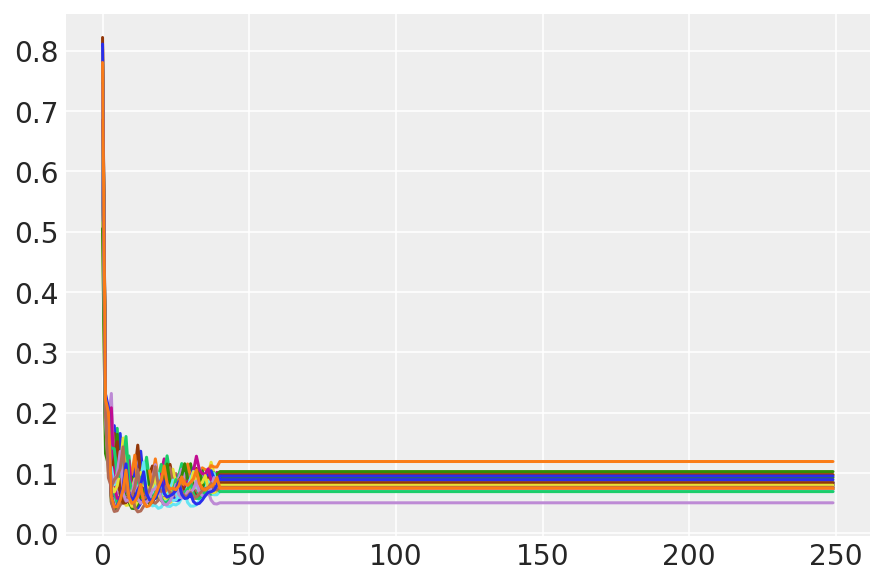
3.7 サンプルを視覚化する
import arviz as az
az.style.use('arviz-darkgrid')
var_name = ['tau', 'initial_cases', 'psi', 'kappa', 'mu', 'alpha', 'ifr_noise']
posterior = {k: np.swapaxes(v.numpy()[burnin:], 1, 0)
for k, v in zip(var_name, samples)}
posterior_with_warmup = {k: np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
チェーンの要約を計算します。高い ESS と 1 に近い r_hat を探しています。
az.summary(posterior)
az_trace = az.from_dict(posterior=posterior_with_warmup,
sample_stats={'diverging': np.swapaxes(sampler_stat['diverging'].numpy(), 0, 1)})
az.plot_trace(az_trace, combined=True, compact=True, figsize=(12, 8));
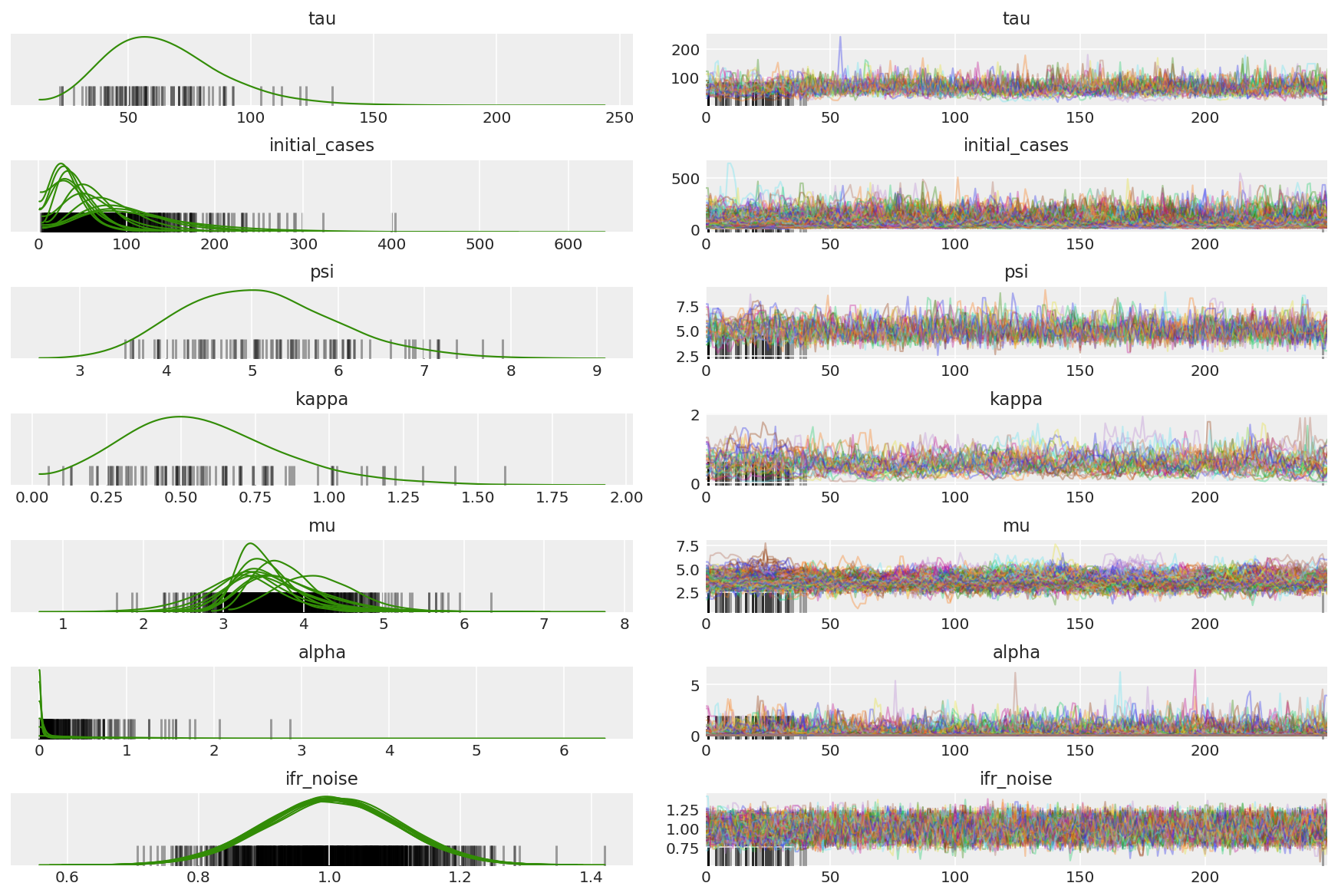
すべての次元にわたる自己相関関数を確認することは有益です。すぐに下降しても負になるほどではない関数(HMC が共振にぶつかることを示し、エルゴード性に悪影響を与えてバイアスを導入する可能性がある)を探しています。
with az.rc_context(rc={'plot.max_subplots': None}):
az.plot_autocorr(posterior, combined=True, figsize=(12, 16), textsize=12);

4 結果
次のプロットは、Flaxman et al. (2020) と同様に、\(R_t\)、死亡数、および感染数に対する事後予測分布を分析します。
total_num_samples = np.prod(posterior['mu'].shape[:2])
# Calculate R_t given parameter estimates.
def rt_samples_batched(mu, intervention_indicators, alpha):
linear_prediction = tf.reduce_sum(
intervention_indicators * alpha[..., np.newaxis, np.newaxis, :], axis=-1)
rt_hat = mu[..., tf.newaxis] * tf.exp(-linear_prediction, name='rt')
return rt_hat
alpha_hat = tf.convert_to_tensor(
posterior['alpha'].reshape(total_num_samples, posterior['alpha'].shape[-1]))
mu_hat = tf.convert_to_tensor(
posterior['mu'].reshape(total_num_samples, num_countries))
rt_hat = rt_samples_batched(mu_hat, intervention_indicators, alpha_hat)
sampled_initial_cases = posterior['initial_cases'].reshape(
total_num_samples, num_countries)
sampled_ifr_noise = posterior['ifr_noise'].reshape(
total_num_samples, num_countries)
psi_hat = posterior['psi'].reshape([total_num_samples])
conv_serial_interval = make_conv_serial_interval(INITIAL_DAYS, TOTAL_DAYS)
conv_fatality_rate = make_conv_fatality_rate(infection_fatality_rate, TOTAL_DAYS)
pred_hat = predict_infections(
intervention_indicators, population_value, sampled_initial_cases, mu_hat,
alpha_hat, conv_serial_interval, INITIAL_DAYS, TOTAL_DAYS)
expected_deaths = predict_deaths(pred_hat, sampled_ifr_noise, conv_fatality_rate)
psi_m = psi_hat[np.newaxis, ..., np.newaxis]
probs = tf.clip_by_value(expected_deaths / (expected_deaths + psi_m), 1e-9, 1.)
predicted_deaths = tfd.NegativeBinomial(
total_count=psi_m, probs=probs).sample()
# Predict counterfactual infections/deaths in the absence of interventions
no_intervention_infections = predict_infections(
intervention_indicators,
population_value,
sampled_initial_cases,
mu_hat,
tf.zeros_like(alpha_hat),
conv_serial_interval,
INITIAL_DAYS, TOTAL_DAYS)
no_intervention_expected_deaths = predict_deaths(
no_intervention_infections, sampled_ifr_noise, conv_fatality_rate)
probs = tf.clip_by_value(
no_intervention_expected_deaths / (no_intervention_expected_deaths + psi_m),
1e-9, 1.)
no_intervention_predicted_deaths = tfd.NegativeBinomial(
total_count=psi_m, probs=probs).sample()
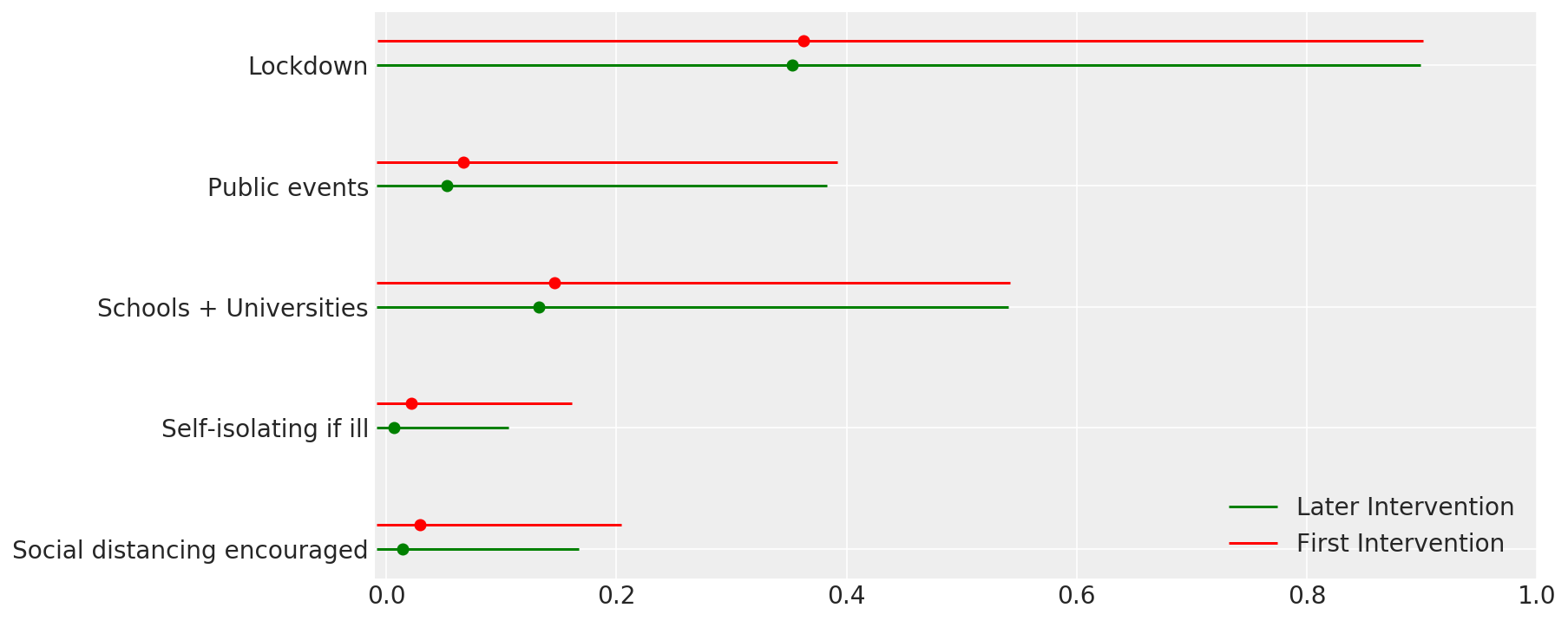
4.1 介入の有効性
Flaxman et al. (2020) の図 4 に似通っています。
def intervention_effectiveness(alpha):
alpha_adj = 1. - np.exp(-alpha + np.log(1.05) / 6.)
alpha_adj_first = (
1. - np.exp(-alpha - alpha[..., -1:] + np.log(1.05) / 6.))
fig, ax = plt.subplots(1, 1, figsize=[12, 6])
intervention_perm = [2, 1, 3, 4, 0]
percentile_vals = [2.5, 97.5]
jitter = .2
for ind in range(5):
first_low, first_high = tfp.stats.percentile(
alpha_adj_first[..., ind], percentile_vals)
low, high = tfp.stats.percentile(
alpha_adj[..., ind], percentile_vals)
p_ind = intervention_perm[ind]
ax.hlines(p_ind, low, high, label='Later Intervention', colors='g')
ax.scatter(alpha_adj[..., ind].mean(), p_ind, color='g')
ax.hlines(p_ind + jitter, first_low, first_high,
label='First Intervention', colors='r')
ax.scatter(alpha_adj_first[..., ind].mean(), p_ind + jitter, color='r')
if ind == 0:
plt.legend(loc='lower right')
ax.set_yticks(range(5))
ax.set_yticklabels(
[any_intervention_list[intervention_perm.index(p)] for p in range(5)])
ax.set_xlim([-0.01, 1.])
r = fig.patch
r.set_facecolor('white')
intervention_effectiveness(alpha_hat)
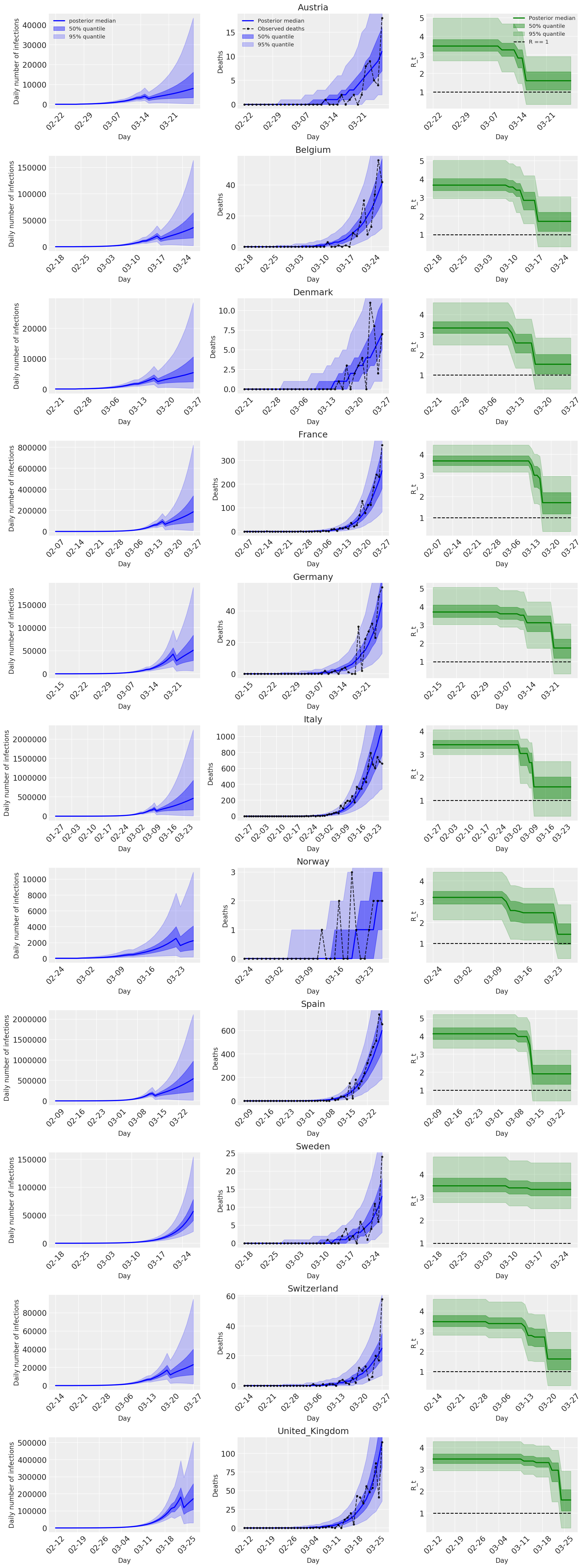
4.2 国別の感染数、死亡数、および R_t
Flaxman et al. (2020) の図 2 に似通っています。
import matplotlib.dates as mdates
plot_quantile = True
forecast_days = 0
fig, ax = plt.subplots(11, 3, figsize=(15, 40))
for ind, country in enumerate(COUNTRIES):
num_days = (pd.to_datetime('2020-03-28') - first_days[country]).days + forecast_days
dates = [(first_days[country] + i*pd.to_timedelta(1, 'days')).strftime('%m-%d') for i in range(num_days)]
plot_dates = [dates[i] for i in range(0, num_days, 7)]
# Plot daily number of infections
infections = pred_hat[:, :, ind]
posterior_quantile = np.percentile(infections, [2.5, 25, 50, 75, 97.5], axis=-1)
ax[ind, 0].plot(
dates, posterior_quantile[2, :num_days],
color='b', label='posterior median', lw=2)
if plot_quantile:
ax[ind, 0].fill_between(
dates, posterior_quantile[1, :num_days], posterior_quantile[3, :num_days],
color='b', label='50% quantile', alpha=.4)
ax[ind, 0].fill_between(
dates, posterior_quantile[0, :num_days], posterior_quantile[4, :num_days],
color='b', label='95% quantile', alpha=.2)
ax[ind, 0].set_xticks(plot_dates)
ax[ind, 0].xaxis.set_tick_params(rotation=45)
ax[ind, 0].set_ylabel('Daily number of infections', fontsize='large')
ax[ind, 0].set_xlabel('Day', fontsize='large')
# Plot deaths
ax[ind, 1].set_title(country)
samples = predicted_deaths[:, :, ind]
posterior_quantile = np.percentile(samples, [2.5, 25, 50, 75, 97.5], axis=-1)
ax[ind, 1].plot(
range(num_days), posterior_quantile[2, :num_days],
color='b', label='Posterior median', lw=2)
if plot_quantile:
ax[ind, 1].fill_between(
range(num_days), posterior_quantile[1, :num_days], posterior_quantile[3, :num_days],
color='b', label='50% quantile', alpha=.4)
ax[ind, 1].fill_between(
range(num_days), posterior_quantile[0, :num_days], posterior_quantile[4, :num_days],
color='b', label='95% quantile', alpha=.2)
observed = deaths[ind, :]
observed[observed == -1] = np.nan
ax[ind, 1].plot(
dates, observed[:num_days],
'--o', color='k', markersize=3,
label='Observed deaths', alpha=.8)
ax[ind, 1].set_xticks(plot_dates)
ax[ind, 1].xaxis.set_tick_params(rotation=45)
ax[ind, 1].set_title(country)
ax[ind, 1].set_xlabel('Day', fontsize='large')
ax[ind, 1].set_ylabel('Deaths', fontsize='large')
# Plot R_t
samples = np.transpose(rt_hat[:, ind, :])
posterior_quantile = np.percentile(samples, [2.5, 25, 50, 75, 97.5], axis=-1)
l1 = ax[ind, 2].plot(
dates, posterior_quantile[2, :num_days],
color='g', label='Posterior median', lw=2)
l2 = ax[ind, 2].fill_between(
dates, posterior_quantile[1, :num_days], posterior_quantile[3, :num_days],
color='g', label='50% quantile', alpha=.4)
if plot_quantile:
l3 = ax[ind, 2].fill_between(
dates, posterior_quantile[0, :num_days], posterior_quantile[4, :num_days],
color='g', label='95% quantile', alpha=.2)
l4 = ax[ind, 2].hlines(1., dates[0], dates[-1], linestyle='--', label='R == 1')
ax[ind, 2].set_xlabel('Day', fontsize='large')
ax[ind, 2].set_ylabel('R_t', fontsize='large')
ax[ind, 2].set_xticks(plot_dates)
ax[ind, 2].xaxis.set_tick_params(rotation=45)
fontsize = 'medium'
ax[0, 0].legend(loc='upper left', fontsize=fontsize)
ax[0, 1].legend(loc='upper left', fontsize=fontsize)
ax[0, 2].legend(
bbox_to_anchor=(1., 1.),
loc='upper right',
borderaxespad=0.,
fontsize=fontsize)
plt.tight_layout();
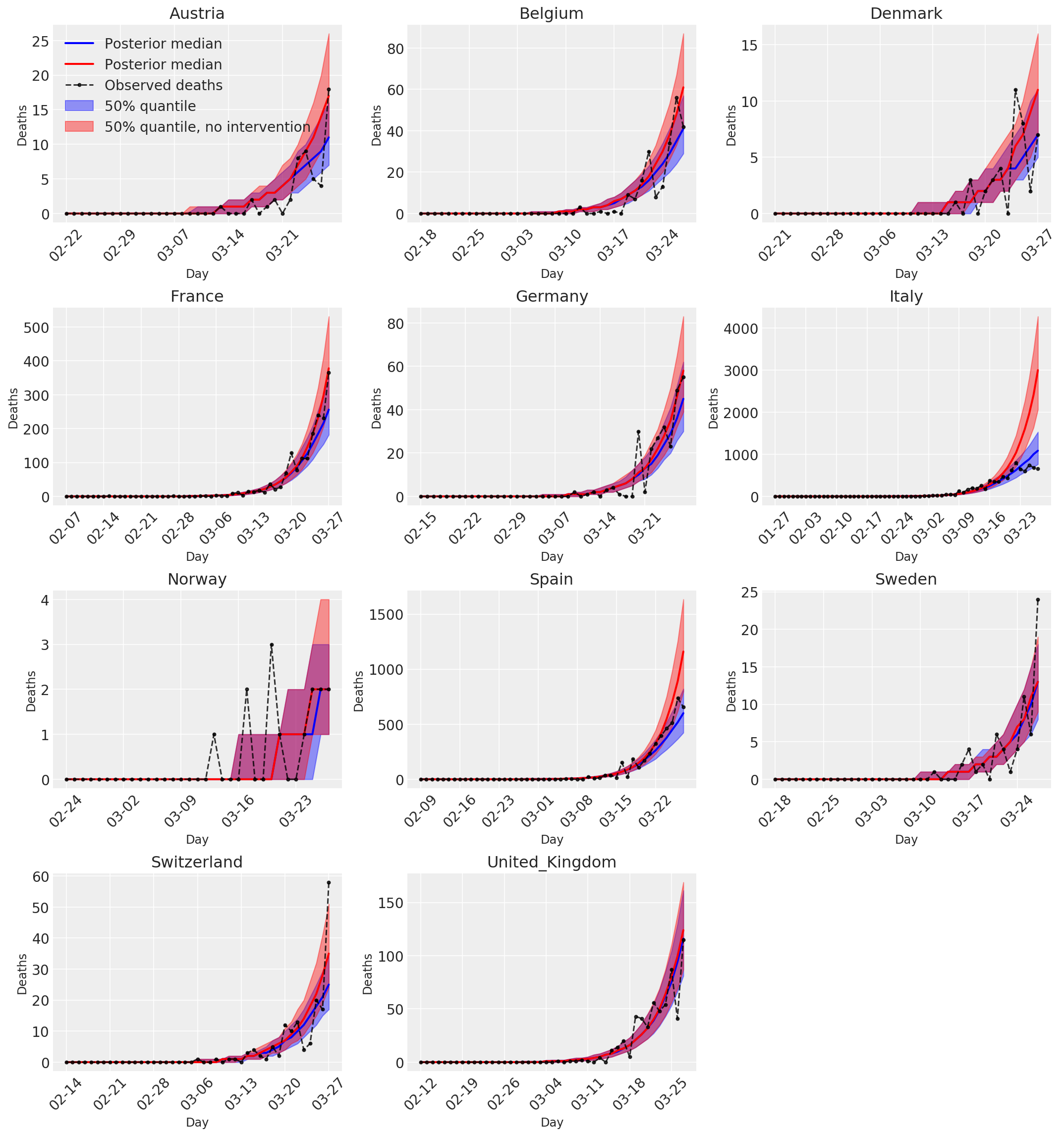
4.3 介入の有無に関わらない 1 日の予測/予想死亡数
plot_quantile = True
forecast_days = 0
fig, ax = plt.subplots(4, 3, figsize=(15, 16))
ax = ax.flatten()
fig.delaxes(ax[-1])
for country_index, country in enumerate(COUNTRIES):
num_days = (pd.to_datetime('2020-03-28') - first_days[country]).days + forecast_days
dates = [(first_days[country] + i*pd.to_timedelta(1, 'days')).strftime('%m-%d') for i in range(num_days)]
plot_dates = [dates[i] for i in range(0, num_days, 7)]
ax[country_index].set_title(country)
quantile_vals = [.025, .25, .5, .75, .975]
samples = predicted_deaths[:, :, country_index].numpy()
quantiles = []
psi_m = psi_hat[np.newaxis, ..., np.newaxis]
probs = tf.clip_by_value(expected_deaths / (expected_deaths + psi_m), 1e-9, 1.)
predicted_deaths_dist = tfd.NegativeBinomial(
total_count=psi_m, probs=probs)
posterior_quantile = np.percentile(samples, [2.5, 25, 50, 75, 97.5], axis=-1)
ax[country_index].plot(
dates, posterior_quantile[2, :num_days],
color='b', label='Posterior median', lw=2)
if plot_quantile:
ax[country_index].fill_between(
dates, posterior_quantile[1, :num_days], posterior_quantile[3, :num_days],
color='b', label='50% quantile', alpha=.4)
samples_counterfact = no_intervention_predicted_deaths[:, :, country_index]
posterior_quantile = np.percentile(samples_counterfact, [2.5, 25, 50, 75, 97.5], axis=-1)
ax[country_index].plot(
dates, posterior_quantile[2, :num_days],
color='r', label='Posterior median', lw=2)
if plot_quantile:
ax[country_index].fill_between(
dates, posterior_quantile[1, :num_days], posterior_quantile[3, :num_days],
color='r', label='50% quantile, no intervention', alpha=.4)
observed = deaths[country_index, :]
observed[observed == -1] = np.nan
ax[country_index].plot(
dates, observed[:num_days],
'--o', color='k', markersize=3,
label='Observed deaths', alpha=.8)
ax[country_index].set_xticks(plot_dates)
ax[country_index].xaxis.set_tick_params(rotation=45)
ax[country_index].set_title(country)
ax[country_index].set_xlabel('Day', fontsize='large')
ax[country_index].set_ylabel('Deaths', fontsize='large')
ax[0].legend(loc='upper left')
plt.tight_layout(pad=1.0);