 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Configurar
Primeiro instale os pacotes usados nesta demonstração.
pip install -q dm-sonnet
Importações (tf, tfp com truque adjunto, etc)
import numpy as np
import tqdm as tqdm
import sklearn.datasets as skd
# visualization
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import kde
# tf and friends
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
import sonnet as snt
tf.enable_v2_behavior()
tfb = tfp.bijectors
tfd = tfp.distributions
def make_grid(xmin, xmax, ymin, ymax, gridlines, pts):
xpts = np.linspace(xmin, xmax, pts)
ypts = np.linspace(ymin, ymax, pts)
xgrid = np.linspace(xmin, xmax, gridlines)
ygrid = np.linspace(ymin, ymax, gridlines)
xlines = np.stack([a.ravel() for a in np.meshgrid(xpts, ygrid)])
ylines = np.stack([a.ravel() for a in np.meshgrid(xgrid, ypts)])
return np.concatenate([xlines, ylines], 1).T
grid = make_grid(-3, 3, -3, 3, 4, 100)
/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead. import pandas.util.testing as tm
Funções auxiliares para visualização
def plot_density(data, axis):
x, y = np.squeeze(np.split(data, 2, axis=1))
levels = np.linspace(0.0, 0.75, 10)
kwargs = {'levels': levels}
return sns.kdeplot(x, y, cmap="viridis", shade=True,
shade_lowest=True, ax=axis, **kwargs)
def plot_points(data, axis, s=10, color='b', label=''):
x, y = np.squeeze(np.split(data, 2, axis=1))
axis.scatter(x, y, c=color, s=s, label=label)
def plot_panel(
grid, samples, transformed_grid, transformed_samples,
dataset, axarray, limits=True):
if len(axarray) != 4:
raise ValueError('Expected 4 axes for the panel')
ax1, ax2, ax3, ax4 = axarray
plot_points(data=grid, axis=ax1, s=20, color='black', label='grid')
plot_points(samples, ax1, s=30, color='blue', label='samples')
plot_points(transformed_grid, ax2, s=20, color='black', label='ode(grid)')
plot_points(transformed_samples, ax2, s=30, color='blue', label='ode(samples)')
ax3 = plot_density(transformed_samples, ax3)
ax4 = plot_density(dataset, ax4)
if limits:
set_limits([ax1], -3.0, 3.0, -3.0, 3.0)
set_limits([ax2], -2.0, 3.0, -2.0, 3.0)
set_limits([ax3, ax4], -1.5, 2.5, -0.75, 1.25)
def set_limits(axes, min_x, max_x, min_y, max_y):
if isinstance(axes, list):
for axis in axes:
set_limits(axis, min_x, max_x, min_y, max_y)
else:
axes.set_xlim(min_x, max_x)
axes.set_ylim(min_y, max_y)
Bijetor FFJORD
Neste colab demonstramos o bijetor FFJORD, originalmente proposto no artigo de Grathwohl, Will, et al. arXiv ligação .
No resumo da idéia por trás dessa abordagem é estabelecer uma correspondência entre a distribuição base conhecida e a distribuição dos dados.
Para estabelecer essa conexão, precisamos
- Definir um mapa bijective \(\mathcal{T}_{\theta}:\mathbf{x} \rightarrow \mathbf{y}\), \(\mathcal{T}_{\theta}^{1}:\mathbf{y} \rightarrow \mathbf{x}\) entre o espaço \(\mathcal{Y}\) no qual a distribuição de base é definida e espaço \(\mathcal{X}\) do domínio de dados.
- Eficientemente acompanhar as deformações que realizamos para transferir a noção de probabilidade para \(\mathcal{X}\).
A segunda condição é formalizada na seguinte expressão para a distribuição de probabilidade definida em \(\mathcal{X}\):
\[ \log p_{\mathbf{x} }(\mathbf{x})=\log p_{\mathbf{y} }(\mathbf{y})-\log \operatorname{det}\left|\frac{\partial \mathcal{T}_{\theta}(\mathbf{y})}{\partial \mathbf{y} }\right| \]
O bijetor FFJORD faz isso definindo uma transformação
\[ \mathcal{T_{\theta} }: \mathbf{x} = \mathbf{z}(t_{0}) \rightarrow \mathbf{y} = \mathbf{z}(t_{1}) \quad : \quad \frac{d \mathbf{z} }{dt} = \mathbf{f}(t, \mathbf{z}, \theta) \]
Esta transformação pode ser invertida, enquanto função \(\mathbf{f}\) descrever a evolução do estado \(\mathbf{z}\) é bom comportamento e o log_det_jacobian pode ser calculada integrando a seguinte expressão.
\[ \log \operatorname{det}\left|\frac{\partial \mathcal{T}_{\theta}(\mathbf{y})}{\partial \mathbf{y} }\right| = -\int_{t_{0} }^{t_{1} } \operatorname{Tr}\left(\frac{\partial \mathbf{f}(t, \mathbf{z}, \theta)}{\partial \mathbf{z}(t)}\right) d t \]
Nesta demo vamos treinar um bijector FFJORD para deformar a distribuição de Gauss para a distribuição definida por moons conjunto de dados. Isso será feito em 3 etapas:
- Definir distribuição base
- Definir bijetor FFJORD
- Minimize a probabilidade de registro exato do conjunto de dados
Primeiro, carregamos os dados
Conjunto de dados
DATASET_SIZE = 1024 * 8
BATCH_SIZE = 256
SAMPLE_SIZE = DATASET_SIZE
moons = skd.make_moons(n_samples=DATASET_SIZE, noise=.06)[0]
moons_ds = tf.data.Dataset.from_tensor_slices(moons.astype(np.float32))
moons_ds = moons_ds.prefetch(tf.data.experimental.AUTOTUNE)
moons_ds = moons_ds.cache()
moons_ds = moons_ds.shuffle(DATASET_SIZE)
moons_ds = moons_ds.batch(BATCH_SIZE)
plt.figure(figsize=[8, 8])
plt.scatter(moons[:, 0], moons[:, 1])
plt.show()

Em seguida, instanciamos uma distribuição de base
base_loc = np.array([0.0, 0.0]).astype(np.float32)
base_sigma = np.array([0.8, 0.8]).astype(np.float32)
base_distribution = tfd.MultivariateNormalDiag(base_loc, base_sigma)
Nós usamos um multi-layer perceptron de modelo state_derivative_fn .
Embora não seja necessário para este conjunto de dados, muitas vezes é benéfico para fazer state_derivative_fn dependente do tempo. Aqui nós conseguir isso concatenando t às entradas de nossa rede.
class MLP_ODE(snt.Module):
"""Multi-layer NN ode_fn."""
def __init__(self, num_hidden, num_layers, num_output, name='mlp_ode'):
super(MLP_ODE, self).__init__(name=name)
self._num_hidden = num_hidden
self._num_output = num_output
self._num_layers = num_layers
self._modules = []
for _ in range(self._num_layers - 1):
self._modules.append(snt.Linear(self._num_hidden))
self._modules.append(tf.math.tanh)
self._modules.append(snt.Linear(self._num_output))
self._model = snt.Sequential(self._modules)
def __call__(self, t, inputs):
inputs = tf.concat([tf.broadcast_to(t, inputs.shape), inputs], -1)
return self._model(inputs)
Parâmetros de modelo e treinamento
LR = 1e-2
NUM_EPOCHS = 80
STACKED_FFJORDS = 4
NUM_HIDDEN = 8
NUM_LAYERS = 3
NUM_OUTPUT = 2
Agora vamos construir uma pilha de bijetores FFJORD. Cada bijector é fornecido com ode_solve_fn e trace_augmentation_fn e é própria state_derivative_fn modelo, de modo que eles representam uma sequência de diferentes transformações.
Bijetor de construção
solver = tfp.math.ode.DormandPrince(atol=1e-5)
ode_solve_fn = solver.solve
trace_augmentation_fn = tfb.ffjord.trace_jacobian_exact
bijectors = []
for _ in range(STACKED_FFJORDS):
mlp_model = MLP_ODE(NUM_HIDDEN, NUM_LAYERS, NUM_OUTPUT)
next_ffjord = tfb.FFJORD(
state_time_derivative_fn=mlp_model,ode_solve_fn=ode_solve_fn,
trace_augmentation_fn=trace_augmentation_fn)
bijectors.append(next_ffjord)
stacked_ffjord = tfb.Chain(bijectors[::-1])
Agora podemos usar TransformedDistribution que é o resultado de entortar base_distribution com stacked_ffjord bijector.
transformed_distribution = tfd.TransformedDistribution(
distribution=base_distribution, bijector=stacked_ffjord)
Agora definimos nosso procedimento de treinamento. Nós simplesmente minimizamos a probabilidade de log negativo dos dados.
Treinamento
@tf.function
def train_step(optimizer, target_sample):
with tf.GradientTape() as tape:
loss = -tf.reduce_mean(transformed_distribution.log_prob(target_sample))
variables = tape.watched_variables()
gradients = tape.gradient(loss, variables)
optimizer.apply(gradients, variables)
return loss
Amostras
@tf.function
def get_samples():
base_distribution_samples = base_distribution.sample(SAMPLE_SIZE)
transformed_samples = transformed_distribution.sample(SAMPLE_SIZE)
return base_distribution_samples, transformed_samples
@tf.function
def get_transformed_grid():
transformed_grid = stacked_ffjord.forward(grid)
return transformed_grid
Plote as amostras das distribuições de base e transformada.
evaluation_samples = []
base_samples, transformed_samples = get_samples()
transformed_grid = get_transformed_grid()
evaluation_samples.append((base_samples, transformed_samples, transformed_grid))
WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/ops/resource_variable_ops.py:1817: calling BaseResourceVariable.__init__ (from tensorflow.python.ops.resource_variable_ops) with constraint is deprecated and will be removed in a future version. Instructions for updating: If using Keras pass *_constraint arguments to layers.
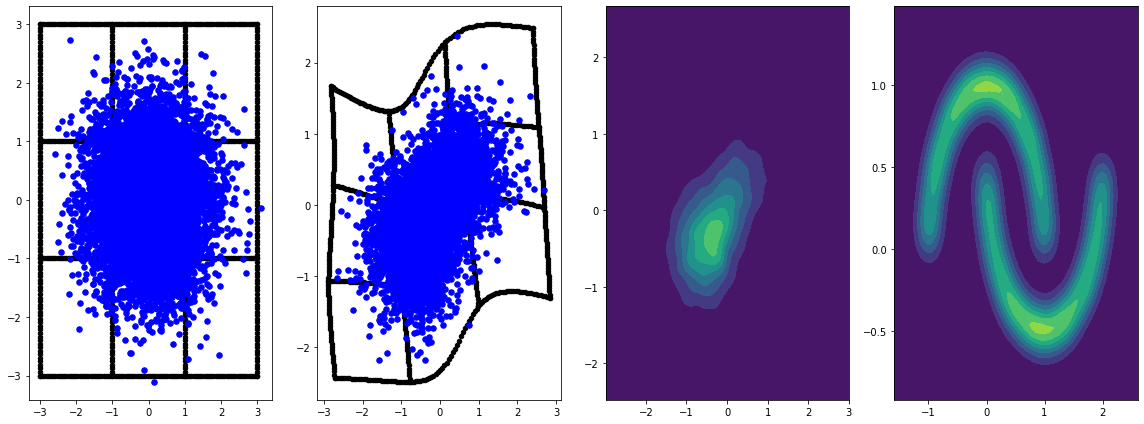
panel_id = 0
panel_data = evaluation_samples[panel_id]
fig, axarray = plt.subplots(
1, 4, figsize=(16, 6))
plot_panel(
grid, panel_data[0], panel_data[2], panel_data[1], moons, axarray, False)
plt.tight_layout()
learning_rate = tf.Variable(LR, trainable=False)
optimizer = snt.optimizers.Adam(learning_rate)
for epoch in tqdm.trange(NUM_EPOCHS // 2):
base_samples, transformed_samples = get_samples()
transformed_grid = get_transformed_grid()
evaluation_samples.append(
(base_samples, transformed_samples, transformed_grid))
for batch in moons_ds:
_ = train_step(optimizer, batch)
0%| | 0/40 [00:00<?, ?it/s] WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow_probability/python/math/ode/base.py:350: calling while_loop_v2 (from tensorflow.python.ops.control_flow_ops) with back_prop=False is deprecated and will be removed in a future version. Instructions for updating: back_prop=False is deprecated. Consider using tf.stop_gradient instead. Instead of: results = tf.while_loop(c, b, vars, back_prop=False) Use: results = tf.nest.map_structure(tf.stop_gradient, tf.while_loop(c, b, vars)) 100%|██████████| 40/40 [07:00<00:00, 10.52s/it]
panel_id = -1
panel_data = evaluation_samples[panel_id]
fig, axarray = plt.subplots(
1, 4, figsize=(16, 6))
plot_panel(grid, panel_data[0], panel_data[2], panel_data[1], moons, axarray)
plt.tight_layout()
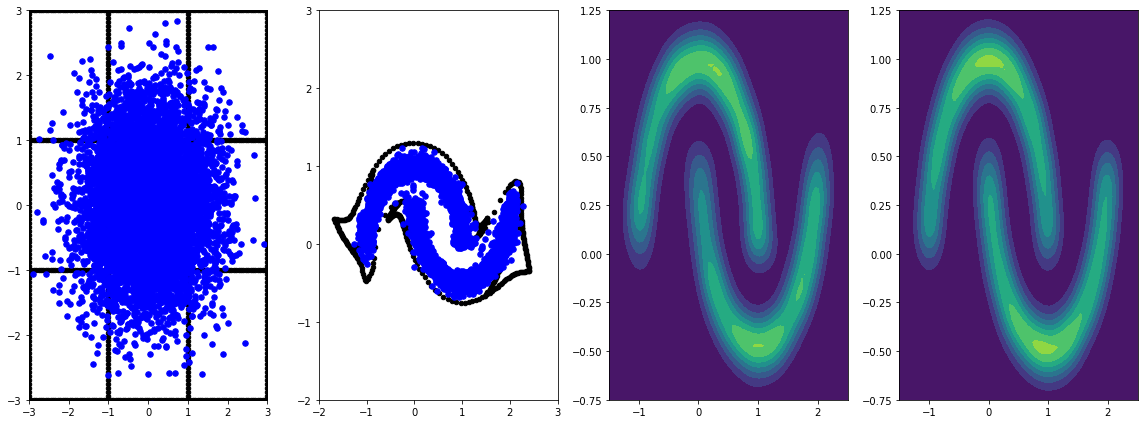
Treinar por mais tempo com a taxa de aprendizagem resulta em melhorias adicionais.
Não convertido neste exemplo, o bijetor FFJORD suporta a estimativa de traço estocástico de Hutchinson. O estimador particular pode ser fornecida através de trace_augmentation_fn . Da mesma forma integradores de alternativas pode ser usado definindo costume ode_solve_fn .

