 TensorFlow.org で表示 TensorFlow.org で表示 |
 Google Colab で実行 Google Colab で実行 |
 GitHub でソースを表示 GitHub でソースを表示 |
 ノートブックをダウンロード ノートブックをダウンロード |
このノートブックは、TensorFlow Probability を学習するためのケーススタディとして作成しました。選択した問題は、2次元平均 0 のガウス型確率変数のサンプルの共分散行列を推定することです。この問題には、いくつかの特徴があります。
- 共分散に逆ウィシャーと分布を使用する場合(一般的なアプローチ)、この問題には分析ソリューションがあるため、結果を確認できます。
- この問題では、制約されたパラメータをサンプリングするため、興味深い複雑さが追加されます。
- ソリューションは、最も単純であっても最速ではないため、最適化を行う必要があります。
私は自分の経験を書き留めることにしました。TFPの細かい部分について頭でまとめるのにしばらく時間がかかったので、このノートブックはかなり単純な説明に始まり、徐々により複雑なTFP機能に移行しています。途中で多くの問題に遭遇しました。それらを特定するのに役立ったプロセスと、最終的に見つけた回避策の両方をキャプチャすることに努めました。また、多くの詳細(各ステップが正しいことを確かめるための多数のテストなど)を含めることにも努めました。
TensorFlow Probability を学習する理由
TensorFlow Probability が自分のプロジェクトに適していると思ったのには、次の理由があります。
- TensorFlow Probability では、ノートブック内でインタラクティブに複雑なモデルをプロトタイプ開発できます。コードを小さなピースに分割してインタラクティブにテストでき、単体テストも実行できます。
- スケールアップの準備ができたら、複数のマシンの複数の最適化されたプロセッサで TensorFlow を実行するために用意されたすべてのインフラストラクチャを利用できます。
- 最後に、私は Stan を非常に気に入ってはいますが、デバッグが非常に困難です。すべてのモデリングコードを、コードを細かく調べたり、中間状態を検査したりできるツールがほとんどないスタンドアロン言語で記述しなくてはいけません。
欠点と言えば、TensorFlow Probability は Stan や PyMC3 よりもずっと新しいため、ドキュメントは制作中であり、構築が必要な機能がまだたくさんありことです。幸いにも、TFP の基盤は固まっており、モジュール式設計であるため、機能をかなり簡単に拡張することができます。このノートブックでは、事例を解決するだけでなく、TFP を拡張する方法についてもいくつか説明します。
対象読者
このノートブックの読者には、以下に示す重要な前提条件を満たしているものとします。
- ベイジアン推論の基礎を理解していること。(理解していない場合は、最初の書籍として『Statistical Rethinking』をお勧めします。)
- Stan / PyMC3 / BUGS など、MCMC サンプリングライブラリにいくらか精通していること。
- NumPy をしっかり把握していること。(導入として『Python for Data Analysis』をお勧めします。)
- 少なくとも TensorFlow をある程度理解している必要はありますが、必ずしも専門知識が必要と言うわけではありません。(『Learning TensorFlow』はお勧めですが、TensorFlow は急速に進化しているため、ほとんどの書籍の情報は少々古いでしょう。スタンフォード大学の CS20 コースもお勧めです。)
最初のトライ
以下は、問題への最初の取り組みです。ネタバレ: 私のソリューションは機能しません。うまく行くまで何度か挑戦しています!プロセスにはしばらくかかりますが、何度か挑戦するたびに、TFP の新たな部分を学習するのに役立ちました。
注意: TFP は現在逆ウィシャート分布を実装していません(最後に、独自の逆ウィシャートを実装する方法を記載しています)。そのため、代わりに、ウィシャート事前分布を使用して精度行列を推定する問題に変更します。
import collections
import math
import os
import time
import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
ステップ 1: 観測をまとめて取得する
私のデータはすべて合成であるため、実世界の例よりも多少整然に見えます。ただし、独自の合成データを生成できない理由はありません。
ヒント: モデルの形態を決定したら、パラメータ値を選択し、モデルを使って合成データを生成できます。次に、実装のサニティーチェックとして、推測に、選択したパラメータの実際値が含まれていることを確認します。デバッグやテストのサイクルを速めるには、簡易バージョンのモデル(次元数またはサンプル数を減らすなど)を検討することをお勧めします。
ヒント: 観測は NumPy 配列として操作するのが最も簡単です。NumPy はデフォルトで float64 を使用するのに対し、TensorFlow はデフォルトで float32 を使用することに注意しておくことが重要です。
一般的に TensorFlow 演算は、すべての引数に同じ型を使用することを求めているため、型を変更するには、明示的にデータをキャストする必要があります。float64 観測を使用する場合には、大量のキャスト演算を追加しなければなりません。一方 NumPy は、自動的にキャストを実施するため、NumPy データを float32 に変換する方が、TensorFlow で float64 の使用を強制するよりもはるかに簡単です。
パラメータ値を選択する
# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)
# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))
[[4. 1.8] [1.8 1. ]] eigenvalues: [4.843075 0.15692513]
合成観測を生成する
TensorFlow Probability は、データの初期次元がサンプルのインデックスを表現し、最後の次元がサンプルの次元性を表現する手法を取っていることに注意してください。
ここでは、それぞれが長さ 2 のベクトルである 100 個のサンプルが必要です。形状 (100, 2) の配列 my_data を生成します。my_data[i, :] は、\(i\) 番目のサンプルであり、長さ 2 のベクトルです。
(my_data の型を忘れずに float32 にしてください!)
# Set the seed so the results are reproducible.
np.random.seed(123)
# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
mean=true_mean, cov=true_cov, size=100,
check_valid='ignore').astype(np.float32)
my_data.shape
(100, 2)
観測をサニティーチェックする
バグの潜在的な原因の 1 つは、合成データの破損です!単純なチェックを行いましょう。
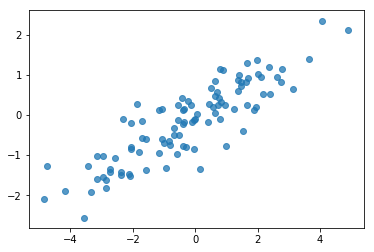
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()
print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)
mean of observations: [-0.24009615 -0.16638893] true mean: [0. 0.]
print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)
covariance of observations: [[3.95307734 1.68718486] [1.68718486 0.94910269]] true covariance: [[4. 1.8] [1.8 1. ]]
サンプルは合理的なようです。次のステップに進みましょう。
ステップ 2: NumPy で尤度関数を実装する
TF Probability で MCMC サンプリングを実行するために記述する必要のある主な内容は、対数尤度関数です。一般的に、NumPy よりも TF の方が記述する際にコツが必要となるため、NumPy に初期の実装を行うのが良いと思います。尤度関数を \(P(data | parameters)\) に対応するデータ尤度関数と、\(P(parameters)\) に対応する事前尤度関数の 2 つに分割することにします。
これらの NumPy 関数は非常に最適化/ベクトル化されている必要なないことに注意してください。単にテスト用に値を生成することが目標であるためです。正確であることが重要です!
まず、データ対数尤度の部分を実装します。これは単純です。注意しておくのは、精度行列を操作しようとしているため、適宜パラメータ化します。
def log_lik_data_numpy(precision, data):
# np.linalg.inv is a really inefficient way to get the covariance matrix, but
# remember we don't care about speed here
cov = np.linalg.inv(precision)
rv = scipy.stats.multivariate_normal(true_mean, cov)
return np.sum(rv.logpdf(data))
# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)
-280.81822950593767
事後分布の分析ソリューションがあるため、精度行列にウィシャート事前分布を使用することにします(Wikipedia の便利な共役事前分布の表をご覧ください)。
ウィシャート分布には、以下の 2 つのパラメータがあります。
- 自由度の数値(Wikipedia では \(\nu\) とラベル付けされています)
- スケール行列(Wikipedia では \(V\) とラベル付けされています)
パラメータ \(\nu のウィシャート分布の平均値 V\) は \(E[W] = \nu V\) で、分散は \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\) です。
有用な直感: ウィシャートサンプルは、平均値 0 と共分散 \(V\) で、多変量正規確率変数から \(\nu\) 個の独立した抽出 \(x_1 \ldots x_{\nu}\) を生成し、和 \(W = \sum_{i=1}^{\nu} x_i x_i^T\) を形成することで、生成することができます。
ウィシャートサンプルを \(\nu\) で除算してスケールし直すと、\(x_i\) のサンプル共分散行列が得られます。このサンプル共分散行列は \(\nu\) が増加するにつれ、\(V\) に向かう傾向になければなりません。\(\nu\) が小さい場合、サンプル共分散行列には多数の変量があるため、小さな値の \(\nu\) はより弱い事前分布に対応し、大きな値の \(\nu\) はより強い事前分布に対応します。\(\nu\) は少なくとも、サンプリングしている空間の次元と同じ大きさである必要があります。そうでない場合、特異行列が生成されます。
\(\nu = 3\) を使用して弱い事前分布とし、共分散推定を単位元の方に引っ張る \(V = \frac{1}{\nu} I\) を取得します(平均は \(\nu V\) です)。
PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF
def log_lik_prior_numpy(precision):
rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
return rv.logpdf(precision)
# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)
-9.103606346649766
ウィシャート分布が、既知の平均 \(\mu\) で多変量正規分布の精度行列を推測するための共役事前分布です。
事前ウィシャートパラメータが \(\nu, V\) であり、多変量正規の \(n\) 個の観測 \(x_1, \ldots, x_n\) があるとすると、事後パラメータは \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\) となります。
n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
(v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))
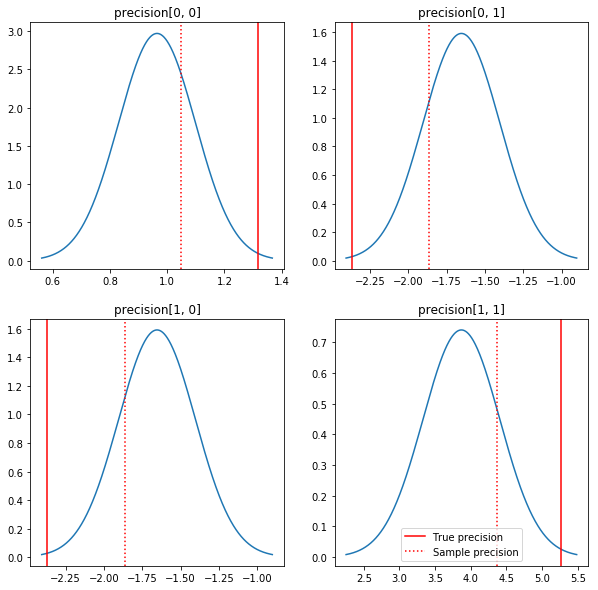
事後分布と実際値を簡単にプロットします。事後分布はサンプル事後分布に近いですが、単位元の方に少し縮約されていることに注意してください。また、実際値は、事後分布のモードから非常に離れていることにも注意してください。おそらくこれは、事前分布がデータにあまり適していないためでしょう。実際の問題では、共分散のスケーリングされた逆ウィシャート事前分布のようなものでうまくいく可能性があります(たとえば、Andrew Gelman のこれに関するコメントをご覧ください)が、そうすると、十分な分析的事後分布は得られません。
sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
for j in range(2):
ax = axes[i, j]
loc = posterior_mean[i, j]
scale = posterior_sd[i, j]
xmin = loc - 3.0 * scale
xmax = loc + 3.0 * scale
x = np.linspace(xmin, xmax, 1000)
y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
ax.plot(x, y)
ax.axvline(true_precision[i, j], color='red', label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()
ステップ 3: TensorFlow で尤度関数を実装する
ネタバレ: 最初のトライは機能しません。その理由については以下に説明します。
ヒント: 尤度関数を作成する際は、TensorFlow Eager モードを使用します。Eager モードを使用することで、TF は NumPy のように動作し、すべてを即時に実行します。そのため、Session.run() を使用しなくても、インタラクティブにデバッグすることができます。こちらの注意書きをご覧ください。
はじめに: 分布クラス
TFP には、対数確率の生成に使用する一連の分布クラスがあります。これらのクラスは単一のサンプルではなく、サンプルのテンソルと連携することに注意してください。このため、ベクトル化と関連する高速化が可能になります。
分布は、2 つの異なる方法で、サンプルのテンソルと連携します。これらの 2 つの方法は、単一のスカラーパラメータのある分布を伴う具体的な例で説明するのが最も簡単です。ポワソン分布を使用しますが、これには rate パラメータがあります。
rateパラメータに単一の値を使用してポワソンを作成する場合、そのsample()メソッドへの呼び出しは単一の値を返します。この値はeventと呼ばれており、この場合、イベントはすべてスカラーです。rateパラメータに値のテンソルを使用してポワソンを作成する場合、そのsample()メソッドへの呼び出しは、rate テンソルの各値に 1 つずつ、複数の値を返します。オブジェクトはそれぞれに独自の rate を持つ独立したポワソンの集合として動作し、sample()への呼び出しで返されるそれぞれの値は、これらのポワソンの 1 つに対応します。この独立しているが同様に分布していないイベントの集合は、batchと呼ばれます。sample()メソッドは、空のタプルをデフォルトとするsample_shapeパラメータを取ります。sample_shapeに渡される値が空でない場合、サンプルは複数の batch を返します。この batch の集合はsampleと呼ばれます。
分布の log_prob() メソッドは、sample() がそれを生成する方法と同様にデータを消費します。log_prob() は sample の確率、つまり複数の独立した event の batch の確率を返します。
- スカラー
rateで作成されたポワソンオブジェクトがある場合、各バッチはスカラーとなります。また、サンプルのテンソルを渡すと、同じサイズの対数確率のテンソルが得られます。 rate値の形状Tのテンソルで作成されたポワソンオブジェクトがある場合、各バッチは形状Tのテンソルとなります。形状 D, T のサンプルのテンソルを渡すと、形状 D, T の対数確率のテンソルが得られます。
以下は、これらのケースを説明する例です。イベント、バッチ、および形状に関するより詳細なチュートリアルについては、こちらのノートブックをご覧ください。
# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))
# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters. Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))
print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())
iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385] draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]
データ対数尤度
まず、データ対数尤度関数を実装します。
注意: 分布は入力を検証できますが、デフォルトでは行いません。デバッグ中は絶対に検証を有効にすることをお勧めします!速度が非常に重要である場合は、すべての動作を確認できたら、検証をオフにできます。
VALIDATE_ARGS = True
ALLOW_NAN_STATS = False
NumPy のケースとの重要な違いの 1 つは、TensorFlow 尤度関数は、単一の行列のみではなく、精度行列のベクトルを処理する必要があるということです。複数のチェーンからサンプリングする際は、パラメータのベクトルが使用されます。
精度行列のバッチ(チェーン当たり 1 つの行列)と連携する分布オブジェクトを作成します。
データの対数確率を計算する際は、バッチ変数ごとに 1 つのコピーが存在するように、パラメータと同じ方法でデータを複製する必要があります。複製されたデータぼ形状は、以下のとおりである必要があります。
[sample shape, batch shape, event shape]
このケースのイベント形状は 2 です(2 次元ガウス分布を使用しているため)。サンプル形状は 100 です(100 個のサンプルがあるため)。バッチ形状は、捜査している精度行列の数になります。尤度関数を呼び出すたびにデータを複製するのは無駄な作業なので、予めデータを複製し、複製されたバージョンを渡します。
これは不十分な実装であることに注意してください。MultivariateNormalFullCovariance は、最後の最適化のセクションで説明する他の方法に比べれば高価です。
def log_lik_data(precisions, replicated_data):
n = tf.shape(precisions)[0] # number of precision matrices
# We're estimating a precision matrix; we have to invert to get log
# probabilities. Cholesky inversion should be relatively efficient,
# but as we'll see later, it's even better if we can avoid doing the Cholesky
# decomposition altogether.
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data). We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)
(100, 2, 2)
ヒント: TensorFlow 関数のサニティーチェックをほとんど記述しないのが非常に良いことに気づきました。TF でのベクトル化はエラーになりやすいため、より単純な NumPy 関数が手元にあれば、TF 出力を検証することができます。ちょっとしたユニットテストと考えるとよいでしょう。
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
事前対数尤度
事前分布は、データの複製を気にしなくてよいため比較的簡単です。
@tf.function(autograph=False)
def log_lik_prior(precisions):
rv_precision = tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions)
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]))
print('tensorflow:', lik_tf[i])
0 numpy: -2.2351873809649625 tensorflow: -2.2351875 1 numpy: -9.103606346649766 tensorflow: -9.103608
同時対数尤度関数を構築する
上記のデータ対数尤度関数は観測に依存しますが、サンプルには観測がありません。依存関係は、グローバル変数を使用しなくても、[クロージャ](https://en.wikipedia.org/wiki/Closure_(computer_programming) を使用することで取り除くことができます。クロージャには、内側の関数が必要とする変数を含む環境を構築する外側の関数が伴います。
def get_log_lik(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik(precision):
return log_lik_data(precision, replicated_data) + log_lik_prior(precision)
return _log_lik
ステップ 4: サンプリング
それでは、サンプリングしましょう!単純に行えるよう、1 つのチェーンのみを使用し、単位元行列を出発点として使用します。後の方で、もう少し注意深く行うことにします。
またしても、これは機能しません。例外が発生します。
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.expand_dims(tf.eye(2), axis=0)
# Use expand_dims because we want to pass in a tensor of starting values
log_lik_fn = get_log_lik(my_data, n_chains=1)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
return states
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
Cholesky decomposition was not successful. The input might not be valid.
[[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]
Function call stack:
sample
...
Function call stack:
sample
問題を特定する
InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. このメッセージではよくわかりません。何が起こったのかを突き止められるか見てみましょう。
- エラーになる値を見れるように、各ステップのパラメータを出力します。
- 特定の問題から保護するためにアサーションを追加します。
アサーションは TensorFlow の演算であり、それが実行されるようにして、最適化によってグラフから除外されないようにする必要があるため、コツが必要です。TF アサーションにあまり詳しくない場合は、TensorFlow デバッグに関するこちらの概要に目を通しておく価値があります。tf.control_dependencies を使用して、明示的にアサーションを強制することができます(以下のコードのコメントをご覧ください)。
TensorFlow の Print というネイティブ関数には、アサーションと同じ動作があります。これは演算であるため、実行されるように操作する必要があります。ノートブックで作業する際、Print を使うと余計な問題が起きます。出力は stderr に送信されるにもかかわらず、stderr はセルに表示されないためです。そのため、tf.Print を使用する代わりに、tf.pyfunc を介して独自の TensorFlow print 演算を作成するというコツが必要です。アサーションと同様に、このメソッドが必ず実行されるようにする必要があります。
def get_log_lik_verbose(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
def _log_lik(precisions):
# An internal method we'll make into a TensorFlow operation via tf.py_func
def _print_precisions(precisions):
print('precisions:\n', precisions)
return False # operations must return something!
# Turn our method into a TensorFlow operation
print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)
# Assertions are also operations, and some care needs to be taken to ensure
# that they're executed
assert_op = tf.assert_equal(
precisions, tf.linalg.matrix_transpose(precisions),
message='not symmetrical', summarize=4, name='symmetry_check')
# The control_dependencies statement forces its arguments to be executed
# before subsequent operations
with tf.control_dependencies([print_op, assert_op]):
return (log_lik_data(precisions, replicated_data) +
log_lik_prior(precisions))
return _log_lik
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.eye(2)[tf.newaxis, ...]
log_lik_fn = get_log_lik_verbose(my_data)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[ 0.24315196 -0.2761638 ]
[-0.33882257 0.8622 ]]]
assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
[[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]
Function call stack:
sample
...
Function call stack:
sample
なぜ失敗するのか
サンプラーが試すまったく最初の新しいパラメータ値は非対称行列です。コレスキー分解がエラーになるのは、それが対照(および正定)行列のみに対して定義されているためです。
ここでの問題は、関心のあるパラメータが精度行列であり、精度行列は、実際の対称的な正定である必要があるためです。サンプラーはこの制約をまったく認識していないため(潜在的に勾配を介す場合を除く)、サンプラーが無効の値を提示してしまう可能性が完全にあり、特にステップサイズが大きい場合は例外につながってしまいます。
ハミルトニアンモンテカルロサンプラーを使えば、勾配がパラメータを無効な領域に近づかせないようにするため、非常に小さなステップサイズを使用して、この問題を回避できる可能性がありますが、ステップサイズが小さいということは、収束まで時間が掛かるということになります。メトロポリスヘイスティングスサンプラーであれば、勾配をまったく認識しないため、失敗してしまいます。
バージョン 2: 制約なしパラメータにパラメータ化し直す
上記の問題には単純なソリューションがあります。新しいパラメータにこのような制約がなくなるように、モデルをパラメータ化し直す方法です。TFP には、これを行うためのバイジェクターという便利なツールが用意されています。
バイジェクターを使ってパラメータ化し直す
ここで使用している精度行列は、実際であり対称的である必要があります。私たちが必要としているのは、これらの制約のない代替パラメータ化です。精度行列のコレスキー分解を出発点としましょう。コレスキー因子には、これらは下三角行列であり、対角要素は正であるという制約がそのまま残りますが、コレスキー因子の対角の対数を取得した場合、対数は正である必要があるという制約がなくなります。すると、下三角事前分布を 1 次元ベクトルに平坦化すると、下三角である必要があるという制約がなくなります。この場合の結果は、制約のない長さ 3 のベクトルになります。
(Stan のマニュアルには、変換によってパラメータのさまざまな制約を取り除く方法に関する素晴らしい章があります。)
この再パラメータ化によるデータ対数尤度関数への影響はほとんどありません(変換を反転するだけで、精度行列が返されます)が、事前分布への影響はより複雑です。精度行列の確率はウィシャート分布によって指定されるように指定しました。変換された行列の確率はどうなるでしょうか。
単調関数 \(g\) を 1 次元の確率変数 \(X\), \(Y = g(X)\) に適用すると、\(Y\) の密度は、以下によって得られることを思い出しましょう。
$$ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) $$
\(g^{-1}\) 項の導関数は、\(g\) が局所体積がどのように変化するかを説明しています。高次確率変数の場合、補正計数は、ヤコビアンの行列式 \(g^{-1}\) の絶対値です(こちらを参照)。
逆変換のヤコビアンを対数事前尤度関数に追加する必要があります。幸いにも、この操作は、TFP の Bijector クラスで解決できます。
Bijector クラスは、確率密度関数の変数を変更するために使用する反転可能で滑らかな関数を表現するために使用されます。すべての Bijector には、変換を実行する forward() メソッド、それを反転する inverse() メソッド、および pdf を再パラメータ化する際に必要となるヤコビアン補正を提供する forward_log_det_jacobian() メソッドと inverse_log_det_jacobian() メソッドがあります。
TFP には、Chain 演算子を通じた合成によって組み合わせ、非常に複雑な変換を形成できる一連の便利なバイジェクターが用意されています。ここでのケースでは、以下の 3 つのバイジェクターを合成します(チェーンの演算は右から左に実行されます)。
- 変換の最初のステップは、精度行列にコレスキー分解を実行することです。これを行うためのバイジェクターはありませんが、
CholeskyOuterProductバイジェクターは 2 つのコレスキー因子の積を取ります。そのため、Invert演算子によって、その逆演算を使用できます。 - 次のステップは、コレスキー因子の対角要素の対数を取得することです。これは、
TransformDiagonalバイジェクターと逆Expバイジェクターを通じて行えます。 - 最後に、逆
FillTriangularバイジェクターを使用して、行列の下三角形の部分をベクトルに平坦化します。
# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
# step 3: flatten the lower triangular portion of the matrix
tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
# step 2: take the log of the diagonals
tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
# step 1: decompose the precision matrix into its Cholesky factors
tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])
# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)
# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)
print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()
print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())
single input: m: [[1. 2.] [2. 8.]] precision_to_unconstrained(m): [0.6931472 2. 0. ] inverse(precision_to_unconstrained(m)): [[1. 2.] [2. 8.]] tensor of inputs: m2: [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]] precision_to_unconstrained(m2): [[0.6931472 2. 0. ] [0. 0. 0. ]] inverse(precision_to_unconstrained(m2)): [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]]
TransformedDistribution クラスは、バイジェクターを分布に適用し、log_prob() に必要なヤコビアン補正を行うプロセスを自動化します。新しい事前分布は、次のようになります。
def log_lik_prior_transformed(transformed_precisions):
rv_precision = tfd.TransformedDistribution(
tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS),
bijector=precision_to_unconstrained,
validate_args=VALIDATE_ARGS)
return rv_precision.log_prob(transformed_precisions)
# Check against the numpy implementation. Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow: -0.84889317 1 numpy: -7.305657151741624 tensorflow: -7.305659
データ対数尤度に逆変換を行うだけです。
precision = precision_to_unconstrained.inverse(transformed_precision)
実際には精度行列のコレスキー分解を行いたいので、ここでは、部分逆行列のみを行うのがより効率的と言えるでしょう。ただし、最適化は後で行うことにし、部分逆行列は読者の演習とします。
def log_lik_data_transformed(transformed_precisions, replicated_data):
# We recover the precision matrix by inverting our bijector. This is
# inefficient since we really want the Cholesky decomposition of the
# precision matrix, and the bijector has that in hand during the inversion,
# but we'll worry about efficiency later.
n = tf.shape(transformed_precisions)[0]
precisions = precision_to_unconstrained.inverse(transformed_precisions)
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
transformed_precisions, replicated_data).numpy()
for i in range(precisions.shape[0]):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
もう一度、新しい関数をクロージャで閉包します。
def get_log_lik_transformed(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_transformed(transformed_precisions):
return (log_lik_data_transformed(transformed_precisions, replicated_data) +
log_lik_prior_transformed(transformed_precisions))
return _log_lik_transformed
# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)
[-431.5611]
サンプリング
無効なパラメータ値のせいでサンプラーが破裂することを心配しなくてよくなったので、実際のサンプルを生成することにしましょう。
サンプラーは、制約なしバージョンのパラメータで動作するため、初期値を制約なしバージョンに変換する必要があります。生成するサンプルも制約なしになるため、それらを変換し直すことも必要です。バイジェクターはベクトル化されているので、変換するのは簡単です。
# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_value = initial_value_cholesky.dot(
initial_value_cholesky.T)[np.newaxis, ...]
# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
initial_value).numpy()
# Sample!
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)
num_results = 1000
num_burnin_steps = 1000
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
initial_value_transformed,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=lambda _, pkr: pkr.is_accepted,
seed=123)
# transform samples back to their constrained form
precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
サンプラーの出力の平均を分析事後平均に比較してみましょう!
print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Sample mean: [[ 1.4315274 -0.25587553] [-0.25587553 0.5740424 ]]
まったく外れています!なぜなのか調べましょう。まず、サンプルを確認します。
np.reshape(precision_samples, [-1, 2, 2])
array([[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
...,
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]]], dtype=float32)
おや?すべてが同じ値になっているようです。なぜそうなったのか調べてみましょう。
kernel_results_ 変数は、状態ごとにサンプラーの情報を提供する名前付きのタプルです。ここでは、is_accepted フィールドが重要です。
# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))
[False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False] Fraction of samples accepted: 0.0
すべてのサンプルが拒否されてしまいました!おそらく、ステップサイズが大きすぎたのでしょう。まったく任意に stepsize=0.1 を選択しました。
バージョン 3: 適応ステップサイズでサンプリングする
私が任意に選択したステップサイズでのサンプリングは失敗に終わったため、以下のような計画があります。
- 適応ステップサイズを実装する
- 収束チェックを実行する
適応ステップサイズを実装するために適切なサンプルコードが tensorflow_probability/python/mcmc/hmc.py にあります。以下では、それを適応させました。
ステップごとに個別の sess.run() ステートメントがあることに注意してください。これを使用すると、必要に応じてステップごとの診断を簡単に追加できるため、デバッグの際に非常に役立ちます。たとえば、段階的な進行や各ステップの時間などを示すことができます。
ヒント: サンプリングを台無しにしてしまう一般的な原因は、グラフをループで増大させてしまうことにあります。(セッションを実行する前にグラフを完成させるのは、そういった問題を防止するためです。)ただし、finalize() を使用していない場合、コードが低速するかどうかをチェックする便利なデバッグは、len(mygraph.get_operations()) を介してステップごとにグラフサイズを出力することです。長さが増加すれば、おそらく誤ったことをしています。
ここでは、3 つの独立したチェーンを実行することにします。チェーン間の比較を行うと、収束を確認しやすくなります。
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values = []
for i in range(N_CHAINS):
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)
initial_values_transformed = precision_to_unconstrained.forward(
initial_values).numpy()
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=hmc,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values_transformed,
kernel=adapted_kernel,
trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
parallel_iterations=1)
# transform samples back to their constrained form
precision_samples = precision_to_unconstrained.inverse(states)
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
簡易チェック: サンプリング中の受け入れ率は、目標の 0.651 に近づいています。
print(np.mean(is_accepted))
0.6190666666666667
さらに良いことに、サンプルの平均と標準偏差は、分析ソリューションから期待されるものに近くなっています。
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96426415 -1.6519215 ] [-1.6519215 3.8614824 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13622096 0.25235635] [0.25235635 0.5394968 ]]
収束を確認する
一般にチェックする分析ソリューションは得られないため、サンプラーが収束していることを確認する必要があります。標準的なチェックの 1 つは Gelman-Rubin \(\hat{R}\) 統計ですが、これには複数のサンプリングチェーンが必要です。\(\hat{R}\) は、チェーン間の(平均の)分散が同一分布である場合に予想されるものを超える度合いを測定します。おおよその収束を示すには、1 に近い \(\hat{R}\) の値が使用されます。詳細は源典をご覧ください。
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0038308 1.0005717] [1.0005717 1.0006068]]
モデルの批判
分析ソリューションがないのであれば、実際のモデル批判を行うとよいでしょう。
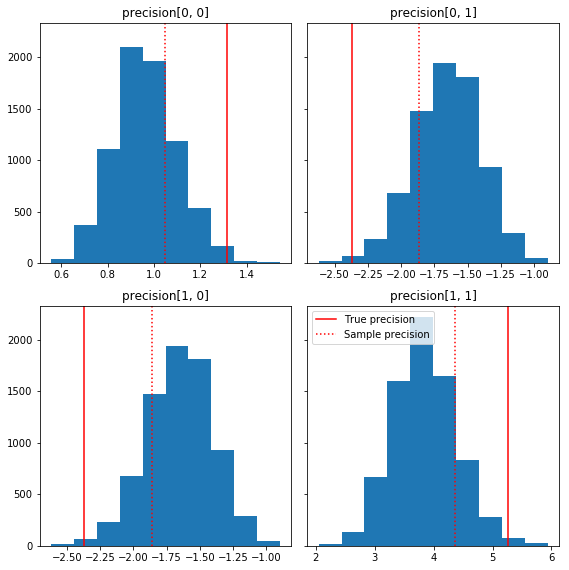
これは、グラウンドトゥルース(赤)に関連するサンプル成分の簡単なヒストグラムです。サンプルがサンプルの精度行列の値から単位元行列事前分布に向かって縮約していることに注意してください。
fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
for j in range(2):
ax = axes[i, j]
ax.hist(precision_samples_reshaped[:, i, j])
ax.axvline(true_precision[i, j], color='red',
label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':',
label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()
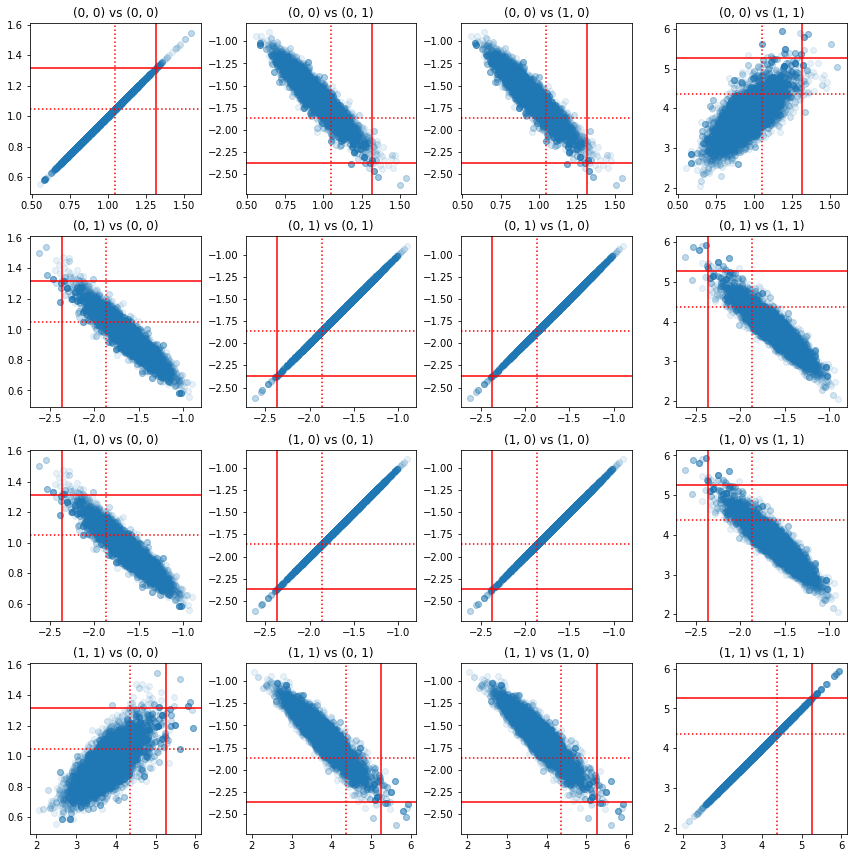
2 組の精度成分の一部の散布図は、事後分布の相関構造により、実際の事後分布の値は、上記の周辺分布からみえるほど、可能性がないわけではないことを示しています。
fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
for j1 in range(2):
index1 = 2 * i1 + j1
for i2 in range(2):
for j2 in range(2):
index2 = 2 * i2 + j2
ax = axes[index1, index2]
ax.scatter(precision_samples_reshaped[:, i1, j1],
precision_samples_reshaped[:, i2, j2], alpha=0.1)
ax.axvline(true_precision[i1, j1], color='red')
ax.axhline(true_precision[i2, j2], color='red')
ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()
バージョン 4: より単純な制約付きパラメータのサンプリング
バイジェクターにより、精度行列のサンプリングは単純になりましたが、制約なしの表現との変換作業が非常に多くありました。それよりももっと簡単な方法があります!
TransformedTransitionKernel
TransformedTransitionKernel は、このプロセスを単純化します。サンプラーを閉包し、すべての変換を行ってくれるのです。引数には、制約なしパラメータの値を制約付きパラメータにマッピングするバイジェクターのリストを取ります。そのため、ここでは上記で使用した precision_to_unconstrained の逆バイジェクターが必要です。tfb.Invert(precision_to_unconstrained) を使用することもできますが、それには逆の逆を行う作業が伴ってしまう(TensorFlow は tf.Invert(tf.Invert()) を tf.Identity()) に単純化するほどスマートではありません)ため、代わりに新しいバイジェクターを作成することにします。
制約付きバイジェクター
# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
# step 3: take the product of Cholesky factors
tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: map a vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()
print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)
m: [[1.0, 2.0], [2.0, 8.0]] unconstrained_to_precision.inverse(m): [0.6931472 2. 0. ] forward(unconstrained_to_precision.inverse(m)): [[1. 2.] [2. 8.]]
TransformedTransitionKernel でサンプリングする
TransformedTransitionKernel を使用すれば、パラメータを手動で変換する必要がなくなります。初期値とサンプルはすべて精度行列です。制約なしのバイジェクターをカーネルに渡せば、カーネルがすべての変換を処理してくれます。
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
return states
precision_samples = sample()
収束を確認する
\(\hat{R}\) 収束チェックは、良い結果を出したようです!
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013582 1.0019467] [1.0019467 1.0011805]]
分析事後分布との比較
もう一度、分析事後分布に対してチェックしてみましょう。
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96687526 -1.6552585 ] [-1.6552585 3.867676 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329624 0.24913791] [0.24913791 0.53983927]]
最適化
エンドツーエンドで動作させることができたので、最適化を行いましょう。この例では速度はそれほど重要ではありませんが、行列が大きくなれば、多少の最適化で大きな違いが現れます。
速度を大幅に改善させる方法の 1 つに、コレスキー分解の観点で再パラメータ化することが挙げられます。その理由は、データ尤度関数に、共分散と精度行列の両方が必要であるためです。逆行列は高価であり(\(n \times n\) 行列に対して \(O(n^3)\))、共分散か精度行列のいずれかに関してパラメータ化すると、もう片方を得るためにインバージョンを行う必要があります。
実際の正定の対称行列 \(M\) は \(M = L L^T\) の積に分解できることを思い出しましょう。ここで、行列 \(L\) は下三角行列であり、正の対角です。\(M\) のコレスキー分解とすると、\(M\)(上と下の三角行列の積)と \(M^{-1}\)(逆置換)の両方をより効率的に取得することができます。コレスキー分解自体は安価に計算できるものではありませんが、コレスキー因子に関してパラメータ化すれば、初期パラメータ値のコレスキー分解のみの計算で済みます。
共分散行列のコレスキー分解を使用する
TFP には多変量正規分布バージョンの MultivariateNormalTriL があり、共分散行列のコレスキー因子に関してパラメータ化されています。そのため、共分散行列のコレスキー因子に関してパラメータ化するのであれば、出た対数尤度を効率的に計算することが可能ということです。課題は、同じような効率で、事前対数尤度を計算することにあります。
サンプルのコレスキー因子で機能する逆ウィシャート分布があれば、完了となりますが、残念ながらありません。(ぜひコードをご提供ください!)代替として、サンプルのコレスキー因子とバイジェクトのチェーンで機能するウィシャート分布を使用することができます。
現時点では、作業を大幅に効率化できる既製のバイジェクターがありませんが、TFP のバイジェクターの力を示す演習と有用な説明として、プロセスをお見せします。
コレスキーインして演算するウィシャート分布
Wishart 分布には、入力と出力の行列がコレスキー因子であることを示す、便利な input_output_cholesky フラグがあります。全行列よりも、コレスキー因子を操作する方がより効率的であり数値的なメリットもあるため、このフラグは有用です。フラグの意味に関する需要なポイント: これは、分布に対して入力と出力の表現が変更することを示すにすぎず、分布の完全な再パラメータ化を示すものではありません。後者を行うには、log_prob() 関数にヤコビアン補正を行う必要があります。実際のところは、この完全な再パラメータ化を行いたいため、独自の分布を構築することにします。
# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices. Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).
class CholeskyWishart(tfd.TransformedDistribution):
"""Wishart distribution reparameterized to use Cholesky factors."""
def __init__(self,
df,
scale_tril,
validate_args=False,
allow_nan_stats=True,
name='CholeskyWishart'):
# Wishart has a bunch of methods that we want to support but not
# implement. We'll subclass TransformedDistribution here to take care of
# those. We'll override the few for which speed is critical and implement
# them with a separate Wishart for which input_output_cholesky=True
super(CholeskyWishart, self).__init__(
distribution=tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=False,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
validate_args=validate_args,
name=name
)
# Here's the Cholesky distribution we'll use for log_prob() and sample()
self.cholesky = tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=True,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats)
def _log_prob(self, x):
return (self.cholesky.log_prob(x) +
self.bijector.inverse_log_det_jacobian(x, event_ndims=2))
def _sample_n(self, n, seed=None):
return self.cholesky._sample_n(n, seed)
# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
@tf.function(autograph=False)
def compute_log_prob(m):
w_transformed = tfd.TransformedDistribution(
tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
w_optimized = CholeskyWishart(
df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
log_prob_transformed = w_transformed.log_prob(m)
log_prob_optimized = w_optimized.log_prob(m)
return log_prob_transformed, log_prob_optimized
for matrix in [np.eye(2, dtype=np.float32),
np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
log_prob_transformed, log_prob_optimized = [
t.numpy() for t in compute_log_prob(matrix)]
print('Transformed Wishart:', log_prob_transformed)
print('Optimized Wishart', log_prob_optimized)
Transformed Wishart: -0.84889317 Optimized Wishart -0.84889317 Transformed Wishart: -99.269455 Optimized Wishart -99.269455
逆ウィシャート分布を構築する
共分散行列 \(C\) を \(C = L L^T\) に分解しました。\(L\) は下三角行列で、正の対角を持ちます。知りたいのは、\(C \sim W^{-1}(\nu, V)\) である場合の \(L\) の確率です。\(W^{-1}\) は逆ウィシャート分布です。
逆ウィシャート分布には、\(C \sim W^{-1}(\nu, V)\) であれば精度行列 \(C^{-1} \sim W(\nu, V^{-1})\) であるプロパティがあります。そのため、ウィシャート分布をパラメータとして取る TransformedDistribution と精度行列のコレスキー因子をその逆行列のコレスキー因子にマッピングするバイジェクターを介して、\(L\) の確率を得ることができます。
\(C^{-1}\) のコレスキー因子から \(C^{-1}\) を取得する単純な(非常に効率的な)方法は、逆解決によってコレスキー因子を逆転し、逆転されたこれらの因子から共分散行列を作成し、その後でコレスキー分解を行うことです。
\(C^{-1} = M M^T\) のコレスキー分解を行いましょう。\(M\) は下三角行列であるため、MatrixInverseTriL バイジェクターを使って逆転させることができます。
\(M^{-1}\) から \(C\) を作成するには、少しコツが要ります。\(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\) です。\(M\) は下三角行列であるため \(M^{-1}\) も下三角行列になり、\(M^{-T}\) は上三角行列になります。CholeskyOuterProduct() バイジェクターは下三角行列でのみ機能するため、\(M^{-T}\) から \(C\) を作成するためには使用できません。回避策は、行列の行と列をパーミュートするバイジェクターのチェーンとなります。
幸いなことに、このロジックは、CholeskyToInvCholesky バイジェクターにカプセル化されています!
すべてのピースを組み合わせる
# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()
print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)
numpy = [[ 1.0307764 0. ] [-0.03031695 0.12126781]] bijector = [[ 1.0307764 0. ] [-0.03031695 0.12126781]]
最終的な分布
コレスキー因子で動作する逆ウィシャートは次のとおりです。
inverse_wishart_cholesky = tfd.TransformedDistribution(
distribution=CholeskyWishart(
df=PRIOR_DF,
scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
bijector=tfb.CholeskyToInvCholesky())
求めていた逆ウィシャートを得ることはできましたが、バイジェクターでコレスキー分解を行う必要があるため、なんとなく低速です。精度行列のパラメータ化に戻って、どのように最適化できるのかを見てみましょう。
最終バージョン!: 精度行列のコレスキー分解を使用する
代替アプローチは、精度行列のコレスキー因子を操作する方法です。ここでは、事前尤度関数が簡単に計算できますが、TFP には精度によってパラメータ化される多変量正規分布バージョンがないため、データ対数尤度関数にはもっと手がかかります。
最適化された事前対数尤度
上記で作成した CholeskyWishart 分布を使用して、事前分布を構築します。
# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
def log_lik_prior_cholesky(precisions_cholesky):
rv_precision = CholeskyWishart(
df=PRIOR_DF,
scale_tril=PRIOR_SCALE_CHOLESKY,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions_cholesky)
# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
distribution=tfd.WishartTriL(
df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow slow:', lik_tf_slow[i])
print('tensorflow fast:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow slow: -0.84889317 tensorflow fast: -0.84889317 1 numpy: -7.442875031036973 tensorflow slow: -7.442877 tensorflow fast: -7.442876
最適化されたデータ対数尤度
TFP のバイジェクターを使用して、独自の多変量正規分布を構築することができます。以下に主な構想を示します。
列ベクトル \(X\) があり、その要素は \(N(0, 1)\) の iid サンプルであるとすると、\(\text{mean}(X) = 0\) と \(\text{cov}(X) = I\) となります。
次に、\(Y = A X + b\) とすると、\(\text{mean}(Y) = b\) と \(\text{cov}(Y) = A A^T\) となります。
したがって、アフィン変換 \(Ax+b\) を使用して、平均 \(b\) と共分散 \(C\) のベクトルを \(A A^T = C\) でて供される iid 標準正規分布のベクトルにすることができます。\(C\) のコレスキー分解には希望するプロパティがありますが、他のソリューションがあります。
\(P = C^{-1}\) 、および \(P\) のコレスキー分解を \(B\) とします。つまり、\(B B^T = P\) です。すると、以下のようになります。
\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)
したがって、目的の平均と共分散を取得するもう一つの方法は、アフィン変換 \(Y=B^{-T}X + b\) を使用する方法です。
私たちのアプローチ(出典はこちらのノートブック):
tfd.Independent()を使用して、1 次元Normal確率変数のバッチを単一の多次元確率変数に組み合わせます。Independent()のreinterpreted_batch_ndimsパラメータは、イベント次元として解釈し直す必要のあるバッチ次元数です。この場合、長さ 2 の1 次元イベントに変換する長さ 2 の1 次元バッチを作成します。したがってreinterpreted_batch_ndims=1となります。- 目的の共分散を追加するバイジェクターを適用します:
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True))。上記では、iid 正規確率変数に、精度行列 \((B^{-T}X)\) のコレスキー因子の逆行列の転置を掛けていることに注意してください。tfb.Invertは \(B\) を逆転し、adjoint=Trueフラグは転置を実行します。 - 目的のオフセットを追加するバイジェクターを適用します:
tfb.Shift(shift=shift)。逆スケールがシフトに適用されるため(\(y=Ax+b\) の逆は \(x=A^{-1}y - A^{-1}b\) であるため)、最初の逆アフィン変換とは別のステップとしてシフトを実行する必要があることに注意してください。
class MVNPrecisionCholesky(tfd.TransformedDistribution):
"""Multivariate normal parameterized by loc and Cholesky precision matrix."""
def __init__(self, loc, precision_cholesky, name=None):
super(MVNPrecisionCholesky, self).__init__(
distribution=tfd.Independent(
tfd.Normal(loc=tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
adjoint=True)),
]),
name=name)
@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
n = tf.shape(precisions_cholesky)[0] # number of precision matrices
rv_data = MVNPrecisionCholesky(
loc=tf.zeros([n, 2]),
precision_cholesky=precisions_cholesky)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.81824
合成された対数尤度関数
次に、事前分布とデータ対数尤度関数をクロージャ内で組み合わせます。
def get_log_lik_cholesky(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_cholesky(precisions_cholesky):
return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
log_lik_prior_cholesky(precisions_cholesky))
return _log_lik_cholesky
制約付きバイジェクター
サンプルは、有効なコレスキー因子となるように制約されているため、正の対角を持つ下三角行列となります。TransformedTransitionKernel には、制約なしテンソルと目的の制約が付いたテンソルをマッピングするバイジェクターが必要です。バイジェクターの逆からコレスキー分解を除外したので、処理が速くなります。
unconstrained_to_precision_cholesky = tfb.Chain([
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: expand the vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)
precisions_cholesky: [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]] inv: [[ 0.0000000e+00 0.0000000e+00 0.0000000e+00] [ 3.5762781e-07 -2.0647411e+00 1.3721828e-01]] fwd(inv): [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]]
初期値
初期値のテンソルを生成します。コレスキー因子を操作しているため、コレスキー因子の初期値を生成します。
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values_cholesky = []
for i in range(N_CHAINS):
initial_values_cholesky.append(np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)
サンプリング
TransformedTransitionKernel を使用して N_CHAINS チェーンをサンプリングします。
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_cholesky(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
samples = tf.linalg.matmul(states, states, transpose_b=True)
return samples
precision_samples = sample()
収束チェック
簡単な収束チェックは、良い結果を出したようです。
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013583 1.0019467] [1.0019467 1.0011804]]
結果を分析事後分布に比較する
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])
またしても、サンプルの平均と標準偏差は、分析事後分布に一致しています。
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.9668749 -1.6552604] [-1.6552604 3.8676758]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329637 0.24913797] [0.24913797 0.53983945]]
これで完成です!最適化されたサンプラーを動作させることができました。
