 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Este tutorial demonstrará a prática recomendada para modelos de treinamento com privacidade diferencial no nível do usuário usando o Tensorflow federado. Nós vamos usar o algoritmo DP-SGD de Abadi et al., "Deep Aprender com privacidade Diferencial" modificado para nível de usuário DP em um contexto federado em McMahan et al., "Aprendizagem diferencialmente Privada Recurrent idioma Models" .
A privacidade diferencial (DP) é um método amplamente usado para delimitar e quantificar o vazamento de privacidade de dados confidenciais ao realizar tarefas de aprendizagem. Treinar um modelo com DP em nível de usuário garante que é improvável que o modelo aprenda algo significativo sobre os dados de qualquer indivíduo, mas ainda pode (espero!) Aprender os padrões que existem nos dados de muitos clientes.
Vamos treinar um modelo no conjunto de dados EMNIST federado. Existe uma compensação inerente entre utilidade e privacidade, e pode ser difícil treinar um modelo com alta privacidade que tenha um desempenho tão bom quanto um modelo não privado de última geração. Por conveniência neste tutorial, treinaremos por apenas 100 rodadas, sacrificando alguma qualidade para demonstrar como treinar com alta privacidade. Se usássemos mais rodadas de treinamento, certamente poderíamos ter um modelo privado um pouco mais preciso, mas não tão alto quanto um modelo treinado sem DP.
Antes de começarmos
Primeiro, vamos ter certeza de que o notebook está conectado a um back-end que possui os componentes relevantes compilados.
!pip install --quiet --upgrade tensorflow_federated_nightly
!pip install --quiet --upgrade nest-asyncio
import nest_asyncio
nest_asyncio.apply()
Algumas importações serão necessárias para o tutorial. Usaremos tensorflow_federated , a estrutura de código aberto para aprendizado de máquina e outros cálculos em dados descentralizadas, bem como tensorflow_privacy , a biblioteca de código aberto para a implementação e análise de algoritmos diferencialmente privadas em tensorflow.
import collections
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_federated as tff
import tensorflow_privacy as tfp
Execute o seguinte exemplo "Hello World" para certificar-se de que o ambiente TFF está configurado corretamente. Se isso não funcionar, consulte a instalação guia para obter instruções.
@tff.federated_computation
def hello_world():
return 'Hello, World!'
hello_world()
b'Hello, World!'
Baixe e pré-processe o conjunto de dados EMNIST federado.
def get_emnist_dataset():
emnist_train, emnist_test = tff.simulation.datasets.emnist.load_data(
only_digits=True)
def element_fn(element):
return collections.OrderedDict(
x=tf.expand_dims(element['pixels'], -1), y=element['label'])
def preprocess_train_dataset(dataset):
# Use buffer_size same as the maximum client dataset size,
# 418 for Federated EMNIST
return (dataset.map(element_fn)
.shuffle(buffer_size=418)
.repeat(1)
.batch(32, drop_remainder=False))
def preprocess_test_dataset(dataset):
return dataset.map(element_fn).batch(128, drop_remainder=False)
emnist_train = emnist_train.preprocess(preprocess_train_dataset)
emnist_test = preprocess_test_dataset(
emnist_test.create_tf_dataset_from_all_clients())
return emnist_train, emnist_test
train_data, test_data = get_emnist_dataset()
Defina nosso modelo.
def my_model_fn():
model = tf.keras.models.Sequential([
tf.keras.layers.Reshape(input_shape=(28, 28, 1), target_shape=(28 * 28,)),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(10)])
return tff.learning.from_keras_model(
keras_model=model,
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
input_spec=test_data.element_spec,
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
Determine a sensibilidade ao ruído do modelo.
Para obter garantias de DP no nível do usuário, devemos alterar o algoritmo básico da Média Federada de duas maneiras. Primeiro, as atualizações do modelo dos clientes devem ser cortadas antes da transmissão para o servidor, limitando a influência máxima de qualquer cliente. Em segundo lugar, o servidor deve adicionar ruído suficiente à soma das atualizações do usuário antes de calcular a média para obscurecer a influência do cliente no pior caso.
Por recorte, que utiliza o método de recorte adaptativo de Andrew et al. 2021, diferencialmente Privada Aprender com Adaptive Clipping , de forma nenhuma norma recorte precisa ser explicitamente definido.
Adicionar ruído geralmente degradará a utilidade do modelo, mas podemos controlar a quantidade de ruído na atualização média em cada rodada com dois botões: o desvio padrão do ruído gaussiano adicionado à soma e o número de clientes no média. Nossa estratégia será primeiro determinar quanto ruído o modelo pode tolerar com um número relativamente pequeno de clientes por rodada com perda aceitável para a utilidade do modelo. Então, para treinar o modelo final, podemos aumentar a quantidade de ruído na soma, enquanto aumentamos proporcionalmente o número de clientes por rodada (assumindo que o conjunto de dados seja grande o suficiente para suportar tantos clientes por rodada). É improvável que isso afete significativamente a qualidade do modelo, uma vez que o único efeito é diminuir a variância devido à amostragem do cliente (na verdade, verificaremos que isso não ocorre em nosso caso).
Para isso, treinamos primeiro uma série de modelos com 50 clientes por rodada, com níveis crescentes de ruído. Especificamente, aumentamos o "noise_multiplier" que é a proporção do desvio padrão do ruído para a norma de corte. Como estamos usando recorte adaptativo, isso significa que a magnitude real do ruído muda de redondo para redondo.
# Run five clients per thread. Increase this if your runtime is running out of
# memory. Decrease it if you have the resources and want to speed up execution.
tff.backends.native.set_local_python_execution_context(clients_per_thread=5)
total_clients = len(train_data.client_ids)
def train(rounds, noise_multiplier, clients_per_round, data_frame):
# Using the `dp_aggregator` here turns on differential privacy with adaptive
# clipping.
aggregation_factory = tff.learning.model_update_aggregator.dp_aggregator(
noise_multiplier, clients_per_round)
# We use Poisson subsampling which gives slightly tighter privacy guarantees
# compared to having a fixed number of clients per round. The actual number of
# clients per round is stochastic with mean clients_per_round.
sampling_prob = clients_per_round / total_clients
# Build a federated averaging process.
# Typically a non-adaptive server optimizer is used because the noise in the
# updates can cause the second moment accumulators to become very large
# prematurely.
learning_process = tff.learning.build_federated_averaging_process(
my_model_fn,
client_optimizer_fn=lambda: tf.keras.optimizers.SGD(0.01),
server_optimizer_fn=lambda: tf.keras.optimizers.SGD(1.0, momentum=0.9),
model_update_aggregation_factory=aggregation_factory)
eval_process = tff.learning.build_federated_evaluation(my_model_fn)
# Training loop.
state = learning_process.initialize()
for round in range(rounds):
if round % 5 == 0:
metrics = eval_process(state.model, [test_data])['eval']
if round < 25 or round % 25 == 0:
print(f'Round {round:3d}: {metrics}')
data_frame = data_frame.append({'Round': round,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
# Sample clients for a round. Note that if your dataset is large and
# sampling_prob is small, it would be faster to use gap sampling.
x = np.random.uniform(size=total_clients)
sampled_clients = [
train_data.client_ids[i] for i in range(total_clients)
if x[i] < sampling_prob]
sampled_train_data = [
train_data.create_tf_dataset_for_client(client)
for client in sampled_clients]
# Use selected clients for update.
state, metrics = learning_process.next(state, sampled_train_data)
metrics = eval_process(state.model, [test_data])['eval']
print(f'Round {rounds:3d}: {metrics}')
data_frame = data_frame.append({'Round': rounds,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
return data_frame
data_frame = pd.DataFrame()
rounds = 100
clients_per_round = 50
for noise_multiplier in [0.0, 0.5, 0.75, 1.0]:
print(f'Starting training with noise multiplier: {noise_multiplier}')
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
print()
Starting training with noise multiplier: 0.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.112289384), ('loss', 2.5190482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.19075724), ('loss', 2.2449977)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.18115693), ('loss', 2.163907)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49970612), ('loss', 2.01017)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5333317), ('loss', 1.8350543)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.5828517), ('loss', 1.6551636)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7352077), ('loss', 0.8700141)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7769152), ('loss', 0.6992781)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.8049814), ('loss', 0.62453026)])
Starting training with noise multiplier: 0.5
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.09526841), ('loss', 2.4332638)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.20128821), ('loss', 2.2664592)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.35472178), ('loss', 2.130336)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.5480995), ('loss', 1.9713942)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.42246276), ('loss', 1.8045483)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.624902), ('loss', 1.4785467)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7265625), ('loss', 0.85801566)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.77720904), ('loss', 0.70615387)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7702537), ('loss', 0.72331005)])
Starting training with noise multiplier: 0.75
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.098672606), ('loss', 2.422002)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.11794671), ('loss', 2.2227976)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.3208513), ('loss', 2.083766)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49752644), ('loss', 1.8728142)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5816761), ('loss', 1.6084186)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.62896746), ('loss', 1.378527)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.73153406), ('loss', 0.8705139)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7789724), ('loss', 0.7113147)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.70944357), ('loss', 0.89495045)])
Starting training with noise multiplier: 1.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.12002841), ('loss', 2.60482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.104574844), ('loss', 2.3388205)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.29966694), ('loss', 2.089262)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.4067398), ('loss', 1.9109797)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5123677), ('loss', 1.6472703)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.56416535), ('loss', 1.4362282)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.62323666), ('loss', 1.1682972)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.55968356), ('loss', 1.4779186)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.382837), ('loss', 1.9680436)])
Agora podemos visualizar a precisão do conjunto de avaliação e a perda dessas execuções.
import matplotlib.pyplot as plt
import seaborn as sns
def make_plot(data_frame):
plt.figure(figsize=(15, 5))
dff = data_frame.rename(
columns={'sparse_categorical_accuracy': 'Accuracy', 'loss': 'Loss'})
plt.subplot(121)
sns.lineplot(data=dff, x='Round', y='Accuracy', hue='NoiseMultiplier', palette='dark')
plt.subplot(122)
sns.lineplot(data=dff, x='Round', y='Loss', hue='NoiseMultiplier', palette='dark')
make_plot(data_frame)
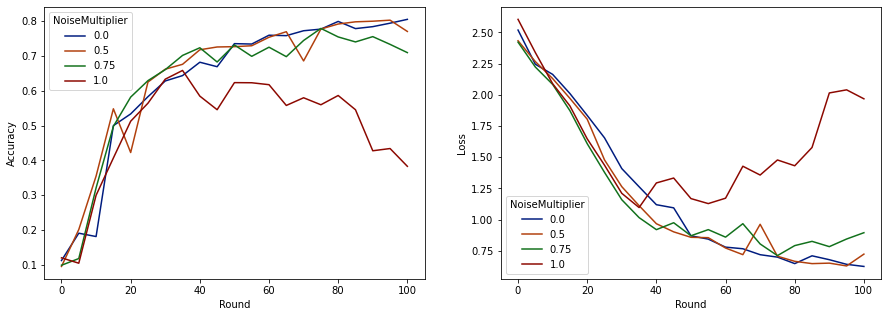
Parece que com 50 clientes esperados por rodada, este modelo pode tolerar um multiplicador de ruído de até 0,5 sem degradar a qualidade do modelo. Um multiplicador de ruído de 0,75 parece causar um pouco de degradação do modelo e 1,0 faz o modelo divergir.
Normalmente, há uma compensação entre qualidade do modelo e privacidade. Quanto mais ruído usarmos, mais privacidade poderemos obter com a mesma quantidade de tempo de treinamento e número de clientes. Por outro lado, com menos ruído, podemos ter um modelo mais preciso, mas teremos que treinar com mais clientes por rodada para atingir nosso nível de privacidade desejado.
Com o experimento acima, podemos decidir que a pequena quantidade de deterioração do modelo em 0,75 é aceitável para treinar o modelo final mais rápido, mas vamos supor que queremos igualar o desempenho do modelo multiplicador de ruído de 0,5.
Agora podemos usar as funções tensorflow_privacy para determinar quantos clientes esperados por rodada precisaríamos para obter privacidade aceitável. A prática padrão é escolher um delta um pouco menor que um em relação ao número de registros no conjunto de dados. Este conjunto de dados tem um total de 3383 usuários de treinamento, então vamos apontar para (2, 1e-5) -DP.
Usamos uma pesquisa binária simples sobre o número de clientes por rodada. A função tensorflow_privacy que usamos para estimar epsilon baseia-se em Wang et al. (2018) e Mironov et al. (2019) .
rdp_orders = ([1.25, 1.5, 1.75, 2., 2.25, 2.5, 3., 3.5, 4., 4.5] +
list(range(5, 64)) + [128, 256, 512])
total_clients = 3383
base_noise_multiplier = 0.5
base_clients_per_round = 50
target_delta = 1e-5
target_eps = 2
def get_epsilon(clients_per_round):
# If we use this number of clients per round and proportionally
# scale up the noise multiplier, what epsilon do we achieve?
q = clients_per_round / total_clients
noise_multiplier = base_noise_multiplier
noise_multiplier *= clients_per_round / base_clients_per_round
rdp = tfp.compute_rdp(
q, noise_multiplier=noise_multiplier, steps=rounds, orders=rdp_orders)
eps, _, _ = tfp.get_privacy_spent(rdp_orders, rdp, target_delta=target_delta)
return clients_per_round, eps, noise_multiplier
def find_needed_clients_per_round():
hi = get_epsilon(base_clients_per_round)
if hi[1] < target_eps:
return hi
# Grow interval exponentially until target_eps is exceeded.
while True:
lo = hi
hi = get_epsilon(2 * lo[0])
if hi[1] < target_eps:
break
# Binary search.
while hi[0] - lo[0] > 1:
mid = get_epsilon((lo[0] + hi[0]) // 2)
if mid[1] > target_eps:
lo = mid
else:
hi = mid
return hi
clients_per_round, _, noise_multiplier = find_needed_clients_per_round()
print(f'To get ({target_eps}, {target_delta})-DP, use {clients_per_round} '
f'clients with noise multiplier {noise_multiplier}.')
To get (2, 1e-05)-DP, use 120 clients with noise multiplier 1.2.
Agora podemos treinar nosso modelo privado final para lançamento.
rounds = 100
noise_multiplier = 1.2
clients_per_round = 120
data_frame = pd.DataFrame()
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
make_plot(data_frame)
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.08260678), ('loss', 2.6334999)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.1492212), ('loss', 2.259542)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.28847474), ('loss', 2.155699)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.3989518), ('loss', 2.0156953)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5086697), ('loss', 1.8261365)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.6204692), ('loss', 1.5602393)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.70008814), ('loss', 0.91155165)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.78421336), ('loss', 0.6820159)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7955525), ('loss', 0.6585961)])
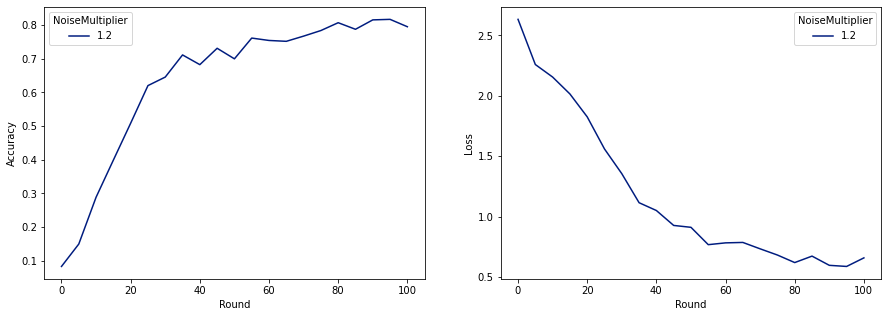
Como podemos ver, o modelo final tem perda e precisão semelhantes ao modelo treinado sem ruído, mas este satisfaz (2, 1e-5) -DP.

