Neural Structured Learning (NSL) koncentruje się na szkoleniu głębokich sieci neuronowych poprzez wykorzystanie sygnałów strukturalnych (jeśli są dostępne) wraz z danymi wejściowymi dotyczącymi funkcji. Jak wprowadzili Bui i in. (WSDM'18) te ustrukturyzowane sygnały służą do regularyzacji uczenia sieci neuronowej, zmuszając model do uczenia się dokładnych przewidywań (poprzez minimalizację nadzorowanych strat), przy jednoczesnym zachowaniu podobieństwa strukturalnego wejścia (poprzez minimalizację utraty sąsiada , patrz rysunek poniżej). Technika ta ma charakter ogólny i można ją zastosować w dowolnych architekturach neuronowych (takich jak sieci NN ze sprzężeniem zwrotnym, sieci konwolucyjne i sieci rekurencyjne).
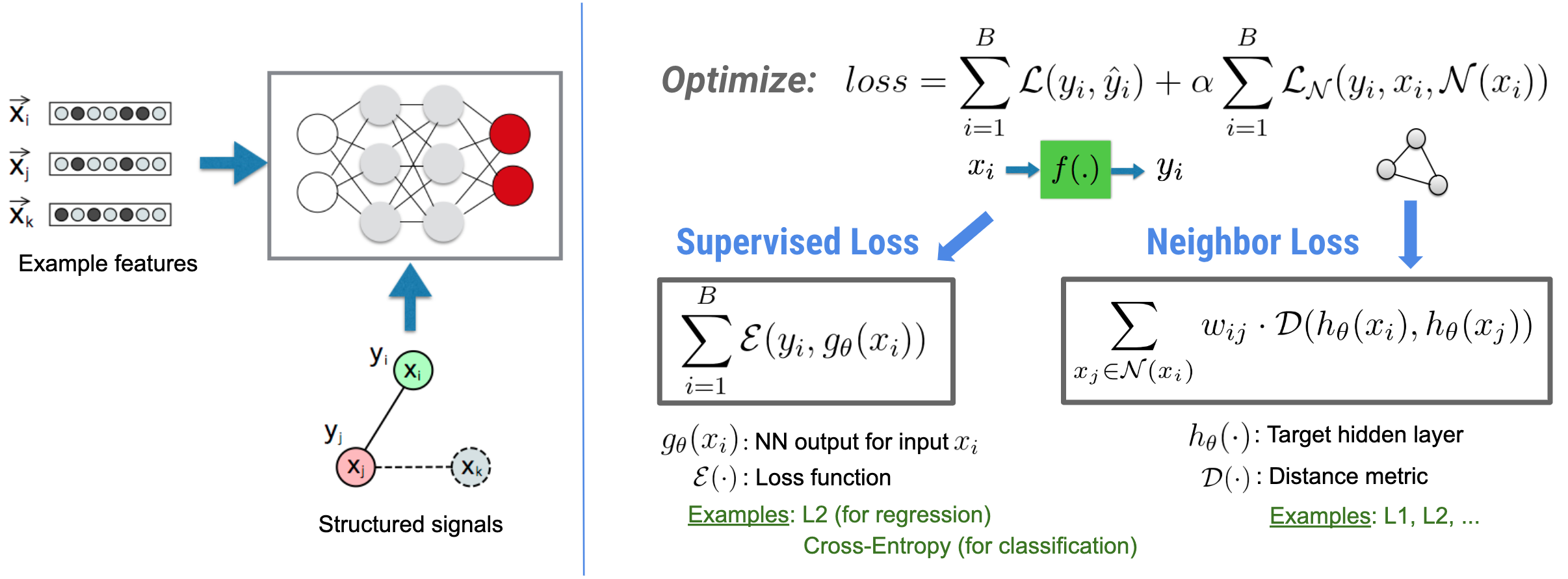
Należy zauważyć, że uogólnione równanie straty sąsiada jest elastyczne i może mieć inne formy oprócz tej zilustrowanej powyżej. Na przykład możemy również wybrać\(\sum_{x_j \in \mathcal{N}(x_i)}\mathcal{E}(y_i,g_\theta(x_j))\) być stratą sąsiada, która oblicza odległość między prawdą podstawową \(y_i\)i przepowiednia sąsiada \(g_\theta(x_j)\). Jest to powszechnie stosowane w uczeniu się kontradyktoryjnym (Goodfellow i in., ICLR'15) . Dlatego NSL uogólnia uczenie się za pomocą grafów neuronowych, jeśli sąsiedzi są wyraźnie reprezentowani przez wykres, oraz uczenie się kontradyktoryjne , jeśli sąsiedzi są pośrednio indukowani przez perturbacje kontradyktoryjne.
Poniżej zilustrowano ogólny przebieg procesu uczenia się o strukturze neuronowej. Czarne strzałki przedstawiają konwencjonalny przebieg szkolenia, a czerwone strzałki przedstawiają nowy przebieg pracy wprowadzony przez NSL w celu wykorzystania sygnałów strukturalnych. Po pierwsze, próbki szkoleniowe są uzupełniane w celu uwzględnienia sygnałów strukturalnych. Jeżeli sygnały strukturalne nie są wyraźnie dostarczone, można je skonstruować lub indukować (to drugie dotyczy uczenia się kontradyktoryjnego). Następnie rozszerzone próbki szkoleniowe (w tym zarówno próbki oryginalne, jak i odpowiadające im sąsiadki) są podawane do sieci neuronowej w celu obliczenia ich osadzania. Obliczana jest odległość pomiędzy osadzeniem próbki a osadzeniem jej sąsiada i wykorzystana jako strata sąsiada, która jest traktowana jako składnik regularyzacyjny i dodawana do straty końcowej. W przypadku jawnej regularyzacji opartej na sąsiadach zazwyczaj obliczamy stratę sąsiada jako odległość między osadzeniem próbki a osadzeniem sąsiada. Jednakże do obliczenia straty sąsiada można zastosować dowolną warstwę sieci neuronowej. Z drugiej strony, w przypadku indukowanej regularyzacji opartej na sąsiadach (kontradykcyjnej) obliczamy stratę sąsiada jako odległość między prognozą wyjściową indukowanego kontradyktoryjnego sąsiada a etykietą prawdy podstawowej.
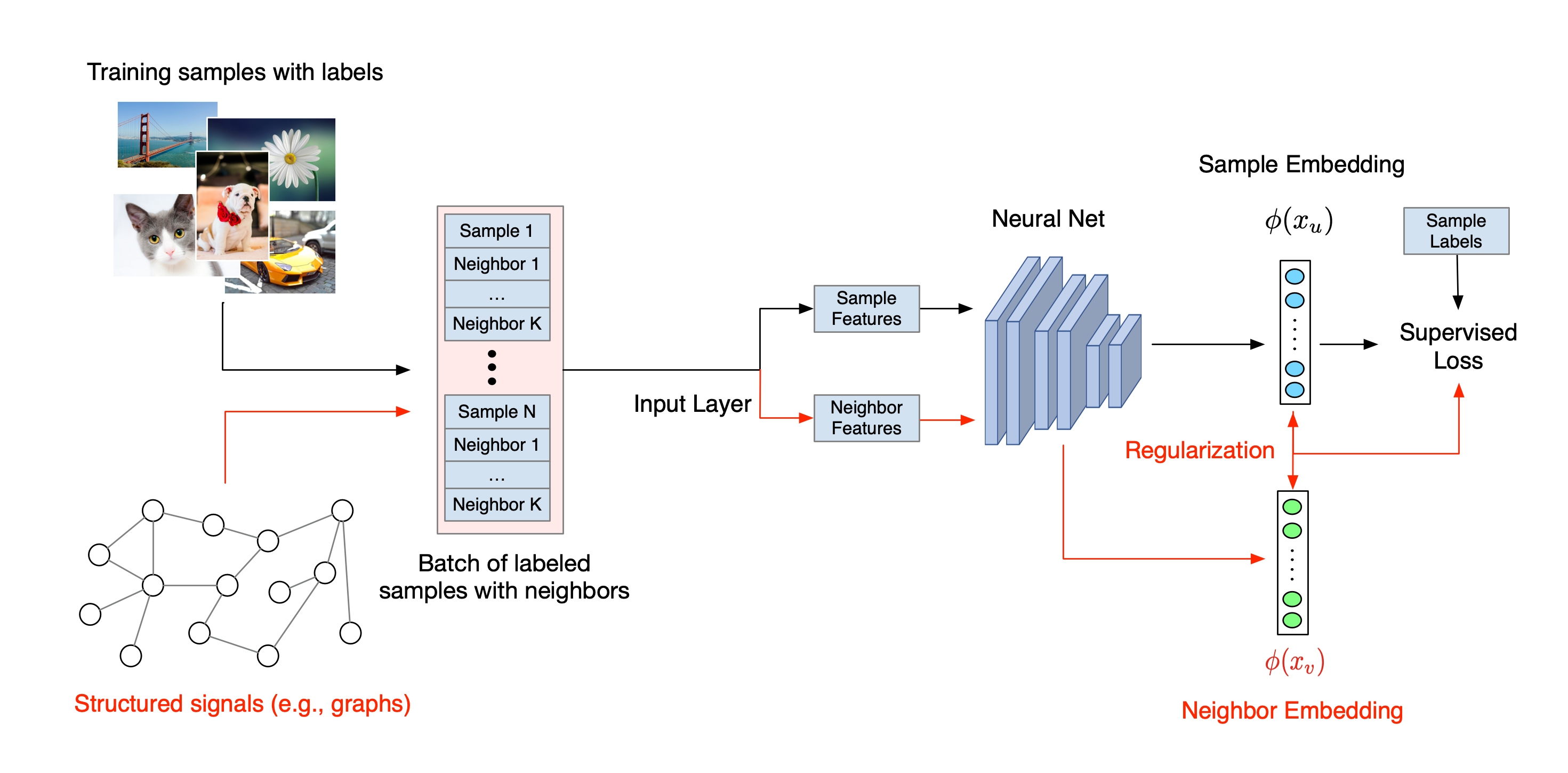
Dlaczego warto używać NSL?
NSL przynosi następujące korzyści:
- Wyższa dokładność : ustrukturyzowane sygnały wśród próbek mogą dostarczyć informacji, które nie zawsze są dostępne na wejściach funkcji; dlatego wykazano, że wspólne podejście do szkolenia (zarówno z sygnałami strukturalnymi, jak i funkcjami) przewyższa wiele istniejących metod (które opierają się wyłącznie na uczeniu z funkcjami) w szerokim zakresie zadań, takich jak klasyfikacja dokumentów i klasyfikacja intencji semantycznych ( Bui i in. ., WSDM'18 i Kipf i in., ICLR'17 ).
- Odporność : wykazano, że modele wyszkolone na kontradyktoryjnych przykładach są odporne na kontradyktoryjne perturbacje mające na celu wprowadzenie w błąd w przewidywaniach lub klasyfikacji modelu ( Goodfellow i in., ICLR'15 & Miyato i in., ICLR'16 ). Gdy liczba próbek uczących jest niewielka, uczenie z przykładami kontradyktoryjnymi pomaga również poprawić dokładność modelu ( Tsipras i in., ICLR'19 ).
- Wymagana mniej oznakowanych danych : NSL umożliwia sieciom neuronowym wykorzystanie zarówno danych oznakowanych, jak i nieoznaczonych, co rozszerza paradygmat uczenia się na uczenie się częściowo nadzorowane . W szczególności NSL pozwala sieci uczyć się przy użyciu oznakowanych danych, tak jak w przypadku ustawień nadzorowanych, a jednocześnie zmusza sieć do uczenia się podobnych ukrytych reprezentacji „sąsiadujących próbek”, które mogą mieć etykiety lub nie. Technika ta okazała się bardzo obiecująca w zakresie poprawy dokładności modelu, gdy ilość oznakowanych danych jest stosunkowo niewielka ( Bui i in., WSDM'18 i Miyato i in., ICLR'16 ).
Samouczki krok po kroku
Aby zdobyć praktyczne doświadczenie w nauczaniu strukturalnym neuronowym, przygotowaliśmy samouczki obejmujące różne scenariusze, w których sygnały strukturalne mogą być jawnie podawane, konstruowane lub indukowane. Oto kilka:
Regularyzacja grafów do klasyfikacji dokumentów przy użyciu grafów naturalnych . W tym samouczku omówimy zastosowanie regularyzacji grafów do klasyfikowania dokumentów tworzących naturalny (organiczny) wykres.
Regularyzacja grafów w celu klasyfikacji nastrojów przy użyciu syntezowanych wykresów . W tym samouczku zademonstrujemy użycie regularyzacji grafów do klasyfikowania nastrojów w recenzjach filmów poprzez konstruowanie (syntetyzowanie) ustrukturyzowanych sygnałów.
Uczenie kontradyktoryjne w klasyfikacji obrazów . W tym samouczku omówimy zastosowanie uczenia kontradyktoryjnego (w którym indukowane są sygnały strukturalne) do klasyfikowania obrazów zawierających cyfry.
Więcej przykładów i tutoriali znajdziesz w katalogu przykładów w naszym repozytorium GitHub.
,Neural Structured Learning (NSL) koncentruje się na szkoleniu głębokich sieci neuronowych poprzez wykorzystanie sygnałów strukturalnych (jeśli są dostępne) wraz z danymi wejściowymi dotyczącymi funkcji. Jak wprowadzili Bui i in. (WSDM'18) te ustrukturyzowane sygnały służą do regularyzacji uczenia sieci neuronowej, zmuszając model do uczenia się dokładnych przewidywań (poprzez minimalizację nadzorowanych strat), przy jednoczesnym zachowaniu podobieństwa strukturalnego wejścia (poprzez minimalizację utraty sąsiada , patrz rysunek poniżej). Technika ta ma charakter ogólny i można ją zastosować w dowolnych architekturach neuronowych (takich jak sieci NN ze sprzężeniem zwrotnym, sieci konwolucyjne i sieci rekurencyjne).

Należy zauważyć, że uogólnione równanie straty sąsiada jest elastyczne i może mieć inne formy oprócz tej zilustrowanej powyżej. Na przykład możemy również wybrać\(\sum_{x_j \in \mathcal{N}(x_i)}\mathcal{E}(y_i,g_\theta(x_j))\) być stratą sąsiada, która oblicza odległość między prawdą podstawową \(y_i\)i przepowiednia sąsiada \(g_\theta(x_j)\). Jest to powszechnie stosowane w uczeniu się kontradyktoryjnym (Goodfellow i in., ICLR'15) . Dlatego NSL uogólnia uczenie się za pomocą grafów neuronowych, jeśli sąsiedzi są wyraźnie reprezentowani przez wykres, oraz uczenie się kontradyktoryjne , jeśli sąsiedzi są pośrednio indukowani przez perturbacje kontradyktoryjne.
Poniżej zilustrowano ogólny przebieg procesu uczenia się o strukturze neuronowej. Czarne strzałki przedstawiają konwencjonalny przebieg szkolenia, a czerwone strzałki przedstawiają nowy przebieg pracy wprowadzony przez NSL w celu wykorzystania sygnałów strukturalnych. Po pierwsze, próbki szkoleniowe są uzupełniane w celu uwzględnienia sygnałów strukturalnych. Jeżeli sygnały strukturalne nie są wyraźnie dostarczone, można je skonstruować lub indukować (to drugie dotyczy uczenia się kontradyktoryjnego). Następnie rozszerzone próbki szkoleniowe (w tym zarówno próbki oryginalne, jak i odpowiadające im sąsiadki) są podawane do sieci neuronowej w celu obliczenia ich osadzania. Obliczana jest odległość pomiędzy osadzeniem próbki a osadzeniem jej sąsiada i wykorzystana jako strata sąsiada, która jest traktowana jako składnik regularyzacyjny i dodawana do straty końcowej. W przypadku jawnej regularyzacji opartej na sąsiadach zazwyczaj obliczamy stratę sąsiada jako odległość między osadzeniem próbki a osadzeniem sąsiada. Jednakże do obliczenia straty sąsiada można zastosować dowolną warstwę sieci neuronowej. Z drugiej strony, w przypadku indukowanej regularyzacji opartej na sąsiadach (kontradykcyjnej) obliczamy stratę sąsiada jako odległość między prognozą wyjściową indukowanego kontradyktoryjnego sąsiada a etykietą prawdy podstawowej.

Dlaczego warto używać NSL?
NSL przynosi następujące korzyści:
- Wyższa dokładność : ustrukturyzowane sygnały wśród próbek mogą dostarczyć informacji, które nie zawsze są dostępne na wejściach funkcji; dlatego wykazano, że wspólne podejście do szkolenia (zarówno z sygnałami strukturalnymi, jak i funkcjami) przewyższa wiele istniejących metod (które opierają się wyłącznie na uczeniu z funkcjami) w szerokim zakresie zadań, takich jak klasyfikacja dokumentów i klasyfikacja intencji semantycznych ( Bui i in. ., WSDM'18 i Kipf i in., ICLR'17 ).
- Odporność : wykazano, że modele wyszkolone na kontradyktoryjnych przykładach są odporne na kontradyktoryjne perturbacje mające na celu wprowadzenie w błąd w przewidywaniach lub klasyfikacji modelu ( Goodfellow i in., ICLR'15 & Miyato i in., ICLR'16 ). Gdy liczba próbek uczących jest niewielka, uczenie z przykładami kontradyktoryjnymi pomaga również poprawić dokładność modelu ( Tsipras i in., ICLR'19 ).
- Wymagana mniej oznakowanych danych : NSL umożliwia sieciom neuronowym wykorzystanie zarówno danych oznakowanych, jak i nieoznaczonych, co rozszerza paradygmat uczenia się na uczenie się częściowo nadzorowane . W szczególności NSL pozwala sieci uczyć się przy użyciu oznakowanych danych, tak jak w przypadku ustawień nadzorowanych, a jednocześnie zmusza sieć do uczenia się podobnych ukrytych reprezentacji „sąsiadujących próbek”, które mogą mieć etykiety lub nie. Technika ta okazała się bardzo obiecująca w zakresie poprawy dokładności modelu, gdy ilość oznakowanych danych jest stosunkowo niewielka ( Bui i in., WSDM'18 i Miyato i in., ICLR'16 ).
Samouczki krok po kroku
Aby zdobyć praktyczne doświadczenie w nauczaniu strukturalnym neuronowym, przygotowaliśmy samouczki obejmujące różne scenariusze, w których sygnały strukturalne mogą być jawnie podawane, konstruowane lub indukowane. Oto kilka:
Regularyzacja grafów do klasyfikacji dokumentów z wykorzystaniem grafów naturalnych . W tym samouczku omówimy zastosowanie regularyzacji grafów do klasyfikowania dokumentów tworzących naturalny (organiczny) wykres.
Regularyzacja grafów w celu klasyfikacji nastrojów przy użyciu syntezowanych wykresów . W tym samouczku zademonstrujemy użycie regularyzacji grafów do klasyfikowania nastrojów w recenzjach filmów poprzez konstruowanie (syntetyzowanie) ustrukturyzowanych sygnałów.
Uczenie kontradyktoryjne w klasyfikacji obrazów . W tym samouczku omówimy zastosowanie uczenia kontradyktoryjnego (w którym indukowane są sygnały strukturalne) do klasyfikowania obrazów zawierających cyfry.
Więcej przykładów i tutoriali znajdziesz w katalogu przykładów w naszym repozytorium GitHub.
,Neural Structured Learning (NSL) koncentruje się na szkoleniu głębokich sieci neuronowych poprzez wykorzystanie sygnałów strukturalnych (jeśli są dostępne) wraz z danymi wejściowymi dotyczącymi funkcji. Jak wprowadzili Bui i in. (WSDM'18) te ustrukturyzowane sygnały służą do regularyzacji uczenia sieci neuronowej, zmuszając model do uczenia się dokładnych przewidywań (poprzez minimalizację nadzorowanych strat), przy jednoczesnym zachowaniu podobieństwa strukturalnego wejścia (poprzez minimalizację utraty sąsiada , patrz rysunek poniżej). Technika ta ma charakter ogólny i można ją zastosować w dowolnych architekturach neuronowych (takich jak sieci NN ze sprzężeniem zwrotnym, sieci konwolucyjne i sieci rekurencyjne).

Należy zauważyć, że uogólnione równanie straty sąsiada jest elastyczne i może mieć inne formy oprócz tej zilustrowanej powyżej. Na przykład możemy również wybrać\(\sum_{x_j \in \mathcal{N}(x_i)}\mathcal{E}(y_i,g_\theta(x_j))\) być stratą sąsiada, która oblicza odległość między prawdą podstawową \(y_i\)i przepowiednia sąsiada \(g_\theta(x_j)\). Jest to powszechnie stosowane w uczeniu się kontradyktoryjnym (Goodfellow i in., ICLR'15) . Dlatego NSL uogólnia uczenie się za pomocą grafów neuronowych, jeśli sąsiedzi są wyraźnie reprezentowani przez wykres, oraz uczenie się kontradyktoryjne , jeśli sąsiedzi są pośrednio indukowani przez perturbacje kontradyktoryjne.
Poniżej zilustrowano ogólny przebieg procesu uczenia się o strukturze neuronowej. Czarne strzałki przedstawiają konwencjonalny przebieg szkolenia, a czerwone strzałki przedstawiają nowy przebieg pracy wprowadzony przez NSL w celu wykorzystania sygnałów strukturalnych. Po pierwsze, próbki szkoleniowe są uzupełniane w celu uwzględnienia sygnałów strukturalnych. Jeżeli sygnały strukturalne nie są wyraźnie dostarczone, można je skonstruować lub indukować (to drugie dotyczy uczenia się kontradyktoryjnego). Następnie rozszerzone próbki szkoleniowe (w tym zarówno próbki oryginalne, jak i odpowiadające im sąsiadki) są podawane do sieci neuronowej w celu obliczenia ich osadzania. Obliczana jest odległość pomiędzy osadzeniem próbki a osadzeniem jej sąsiada i wykorzystana jako strata sąsiada, która jest traktowana jako składnik regularyzacyjny i dodawana do straty końcowej. W przypadku jawnej regularyzacji opartej na sąsiadach zazwyczaj obliczamy stratę sąsiada jako odległość między osadzeniem próbki a osadzeniem sąsiada. Jednakże do obliczenia straty sąsiada można zastosować dowolną warstwę sieci neuronowej. Z drugiej strony, w przypadku indukowanej regularyzacji opartej na sąsiadach (kontradykcyjnej) obliczamy stratę sąsiada jako odległość między prognozą wyjściową indukowanego kontradyktoryjnego sąsiada a etykietą prawdy podstawowej.

Dlaczego warto używać NSL?
NSL przynosi następujące korzyści:
- Wyższa dokładność : ustrukturyzowane sygnały wśród próbek mogą dostarczyć informacji, które nie zawsze są dostępne na wejściach funkcji; dlatego wykazano, że wspólne podejście do szkolenia (zarówno z sygnałami strukturalnymi, jak i funkcjami) przewyższa wiele istniejących metod (które opierają się wyłącznie na uczeniu z funkcjami) w szerokim zakresie zadań, takich jak klasyfikacja dokumentów i klasyfikacja intencji semantycznych ( Bui i in. ., WSDM'18 i Kipf i in., ICLR'17 ).
- Odporność : wykazano, że modele wyszkolone na kontradyktoryjnych przykładach są odporne na kontradyktoryjne perturbacje mające na celu wprowadzenie w błąd w przewidywaniach lub klasyfikacji modelu ( Goodfellow i in., ICLR'15 & Miyato i in., ICLR'16 ). Gdy liczba próbek uczących jest niewielka, uczenie z przykładami kontradyktoryjnymi pomaga również poprawić dokładność modelu ( Tsipras i in., ICLR'19 ).
- Wymagana mniej oznakowanych danych : NSL umożliwia sieciom neuronowym wykorzystanie zarówno danych oznakowanych, jak i nieoznaczonych, co rozszerza paradygmat uczenia się na uczenie się częściowo nadzorowane . W szczególności NSL pozwala sieci uczyć się przy użyciu oznakowanych danych, tak jak w przypadku ustawień nadzorowanych, a jednocześnie zmusza sieć do uczenia się podobnych ukrytych reprezentacji „sąsiadujących próbek”, które mogą mieć etykiety lub nie. Technika ta okazała się bardzo obiecująca w zakresie poprawy dokładności modelu, gdy ilość oznakowanych danych jest stosunkowo niewielka ( Bui i in., WSDM'18 i Miyato i in., ICLR'16 ).
Samouczki krok po kroku
Aby zdobyć praktyczne doświadczenie w nauczaniu strukturalnym neuronowym, przygotowaliśmy samouczki obejmujące różne scenariusze, w których sygnały strukturalne mogą być jawnie podawane, konstruowane lub indukowane. Oto kilka:
Regularyzacja grafów do klasyfikacji dokumentów przy użyciu grafów naturalnych . W tym samouczku omówimy zastosowanie regularyzacji grafów do klasyfikowania dokumentów tworzących naturalny (organiczny) wykres.
Regularyzacja grafów w celu klasyfikacji nastrojów przy użyciu syntezowanych wykresów . W tym samouczku zademonstrujemy użycie regularyzacji grafów do klasyfikowania nastrojów w recenzjach filmów poprzez konstruowanie (syntetyzowanie) ustrukturyzowanych sygnałów.
Uczenie kontradyktoryjne w klasyfikacji obrazów . W tym samouczku omówimy zastosowanie uczenia kontradyktoryjnego (w którym indukowane są sygnały strukturalne) do klasyfikowania obrazów zawierających cyfry.
Więcej przykładów i tutoriali znajdziesz w katalogu przykładów w naszym repozytorium GitHub.

