 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
En este colab, exploraremos el muestreo de la parte posterior de un modelo de mezcla gaussiana bayesiana (BGMM) utilizando solo primitivas de probabilidad de TensorFlow.
Modelo
Para \(k\in\{1,\ldots, K\}\) componentes de la mezcla de cada uno de dimensión \(D\), nos gustaría modelo \(i\in\{1,\ldots,N\}\) muestras usando la siguiente mezcla de modelo Bayesiano Gaussian IId:
\[\begin{align*} \theta &\sim \text{Dirichlet}(\text{concentration}=\alpha_0)\\ \mu_k &\sim \text{Normal}(\text{loc}=\mu_{0k}, \text{scale}=I_D)\\ T_k &\sim \text{Wishart}(\text{df}=5, \text{scale}=I_D)\\ Z_i &\sim \text{Categorical}(\text{probs}=\theta)\\ Y_i &\sim \text{Normal}(\text{loc}=\mu_{z_i}, \text{scale}=T_{z_i}^{-1/2})\\ \end{align*}\]
Nota, las scale argumentos, todos tienen cholesky semántica. Usamos esta convención porque es la de las distribuciones TF (que usa esta convención en parte porque es computacionalmente ventajosa).
Nuestro objetivo es generar muestras a partir del posterior:
\[p\left(\theta, \{\mu_k, T_k\}_{k=1}^K \Big| \{y_i\}_{i=1}^N, \alpha_0, \{\mu_{ok}\}_{k=1}^K\right)\]
Tenga en cuenta que \(\{Z_i\}_{i=1}^N\) no está presente - ESTAMOS interesado sólo en aquellas variables aleatorias que no escalan con \(N\). (Y por suerte hay una distribución de TF que se ocupa de marginar a cabo \(Z_i\)).
No es posible muestrear directamente de esta distribución debido a un término de normalización computacionalmente intratable.
Algoritmos Metropolis-Hastings son técnica para para el muestreo a partir de distribuciones-intratables a normalizar.
TensorFlow Probability ofrece una serie de opciones de MCMC, incluidas varias basadas en Metropolis-Hastings. En este cuaderno, usaremos hamiltoniano Monte Carlo ( tfp.mcmc.HamiltonianMonteCarlo ). HMC es a menudo una buena opción porque puede converger rápidamente, muestrea el espacio de estados de forma conjunta (en lugar de coordinarse) y aprovecha una de las virtudes de TF: la diferenciación automática. Dicho esto, a partir de un muestreo posterior BGMM en realidad podría ser mejor hecho por otros enfoques, por ejemplo, el muestreo de Gibbs .
%matplotlib inline
import functools
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import seaborn as sns; sns.set_context('notebook')
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
physical_devices = tf.config.experimental.list_physical_devices('GPU')
if len(physical_devices) > 0:
tf.config.experimental.set_memory_growth(physical_devices[0], True)
Antes de construir realmente el modelo, necesitaremos definir un nuevo tipo de distribución. De la especificación del modelo anterior, está claro que estamos parametrizando el MVN con una matriz de covarianza inversa, es decir, [matriz de precisión] (https://en.wikipedia.org/wiki/Precision_ (estadísticas% 29). Para lograr esto en TF, tendremos que rodar nuestra Bijector Este. Bijector utilizará la transformación hacia adelante:
-
Y = tf.linalg.triangular_solve((tf.linalg.matrix_transpose(chol_precision_tril), X, adjoint=True) + loc.
Y el log_prob cálculo es simplemente la inversa, es decir:
-
X = tf.linalg.matmul(chol_precision_tril, X - loc, adjoint_a=True).
Puesto que todo lo que necesitamos para HMC es log_prob , esto significa que evitan llamar nunca a tf.linalg.triangular_solve (como sería el caso para tfd.MultivariateNormalTriL ). Esto es ventajoso puesto tf.linalg.matmul es generalmente más rápido debido a una mejor localidad caché.
class MVNCholPrecisionTriL(tfd.TransformedDistribution):
"""MVN from loc and (Cholesky) precision matrix."""
def __init__(self, loc, chol_precision_tril, name=None):
super(MVNCholPrecisionTriL, self).__init__(
distribution=tfd.Independent(tfd.Normal(tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=chol_precision_tril,
adjoint=True)),
]),
name=name)
El tfd.Independent distribución vueltas independiente extrae de una distribución, en una distribución multivariante con coordenadas estadísticamente independientes. En términos de cálculo de log_prob , esto manifiesta "meta-distribución" como una suma simple a través de la dimensión evento (s).
También notamos que tomamos el adjoint ( "transposición") de la matriz de escala. Esto es porque si la precisión es de covarianza inversa, es decir, \(P=C^{-1}\) y si \(C=AA^\top\), entonces \(P=BB^{\top}\) donde \(B=A^{-\top}\).
Dado que esta distribución es un poco complicado, vamos a verificar rápidamente que nuestra MVNCholPrecisionTriL funciona como creemos que debería.
def compute_sample_stats(d, seed=42, n=int(1e6)):
x = d.sample(n, seed=seed)
sample_mean = tf.reduce_mean(x, axis=0, keepdims=True)
s = x - sample_mean
sample_cov = tf.linalg.matmul(s, s, adjoint_a=True) / tf.cast(n, s.dtype)
sample_scale = tf.linalg.cholesky(sample_cov)
sample_mean = sample_mean[0]
return [
sample_mean,
sample_cov,
sample_scale,
]
dtype = np.float32
true_loc = np.array([1., -1.], dtype=dtype)
true_chol_precision = np.array([[1., 0.],
[2., 8.]],
dtype=dtype)
true_precision = np.matmul(true_chol_precision, true_chol_precision.T)
true_cov = np.linalg.inv(true_precision)
d = MVNCholPrecisionTriL(
loc=true_loc,
chol_precision_tril=true_chol_precision)
[sample_mean, sample_cov, sample_scale] = [
t.numpy() for t in compute_sample_stats(d)]
print('true mean:', true_loc)
print('sample mean:', sample_mean)
print('true cov:\n', true_cov)
print('sample cov:\n', sample_cov)
true mean: [ 1. -1.] sample mean: [ 1.0002806 -1.000105 ] true cov: [[ 1.0625 -0.03125 ] [-0.03125 0.015625]] sample cov: [[ 1.0641273 -0.03126175] [-0.03126175 0.01559312]]
Dado que la media y la covarianza de la muestra están cerca de la media y la covarianza verdaderas, parece que la distribución se ha implementado correctamente. Ahora, vamos a utilizar MVNCholPrecisionTriL tfp.distributions.JointDistributionNamed para especificar el modelo BGMM. Para el modelo de observación, usaremos tfd.MixtureSameFamily para integrar automáticamente el \(\{Z_i\}_{i=1}^N\) dibuja.
dtype = np.float64
dims = 2
components = 3
num_samples = 1000
bgmm = tfd.JointDistributionNamed(dict(
mix_probs=tfd.Dirichlet(
concentration=np.ones(components, dtype) / 10.),
loc=tfd.Independent(
tfd.Normal(
loc=np.stack([
-np.ones(dims, dtype),
np.zeros(dims, dtype),
np.ones(dims, dtype),
]),
scale=tf.ones([components, dims], dtype)),
reinterpreted_batch_ndims=2),
precision=tfd.Independent(
tfd.WishartTriL(
df=5,
scale_tril=np.stack([np.eye(dims, dtype=dtype)]*components),
input_output_cholesky=True),
reinterpreted_batch_ndims=1),
s=lambda mix_probs, loc, precision: tfd.Sample(tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(probs=mix_probs),
components_distribution=MVNCholPrecisionTriL(
loc=loc,
chol_precision_tril=precision)),
sample_shape=num_samples)
))
def joint_log_prob(observations, mix_probs, loc, chol_precision):
"""BGMM with priors: loc=Normal, precision=Inverse-Wishart, mix=Dirichlet.
Args:
observations: `[n, d]`-shaped `Tensor` representing Bayesian Gaussian
Mixture model draws. Each sample is a length-`d` vector.
mix_probs: `[K]`-shaped `Tensor` representing random draw from
`Dirichlet` prior.
loc: `[K, d]`-shaped `Tensor` representing the location parameter of the
`K` components.
chol_precision: `[K, d, d]`-shaped `Tensor` representing `K` lower
triangular `cholesky(Precision)` matrices, each being sampled from
a Wishart distribution.
Returns:
log_prob: `Tensor` representing joint log-density over all inputs.
"""
return bgmm.log_prob(
mix_probs=mix_probs, loc=loc, precision=chol_precision, s=observations)
Generar datos de "entrenamiento"
Para esta demostración, probaremos algunos datos aleatorios.
true_loc = np.array([[-2., -2],
[0, 0],
[2, 2]], dtype)
random = np.random.RandomState(seed=43)
true_hidden_component = random.randint(0, components, num_samples)
observations = (true_loc[true_hidden_component] +
random.randn(num_samples, dims).astype(dtype))
Inferencia bayesiana mediante HMC
Ahora que usamos TFD para especificar nuestro modelo y obtuvimos algunos datos observados, tenemos todas las piezas necesarias para ejecutar HMC.
Para ello, vamos a utilizar una aplicación parcial de "Inmovilizar" las cosas que no queremos a la muestra. En este caso, eso significa que sólo necesitan precisar observations . (Los hiper-parámetros ya se cuecen en a las distribuciones previas y no forma parte del joint_log_prob firma de función.)
unnormalized_posterior_log_prob = functools.partial(joint_log_prob, observations)
initial_state = [
tf.fill([components],
value=np.array(1. / components, dtype),
name='mix_probs'),
tf.constant(np.array([[-2., -2],
[0, 0],
[2, 2]], dtype),
name='loc'),
tf.linalg.eye(dims, batch_shape=[components], dtype=dtype, name='chol_precision'),
]
Representación sin restricciones
Hamiltonian Monte Carlo (HMC) requiere que la función logarítmica de probabilidad objetivo sea diferenciable con respecto a sus argumentos. Además, HMC puede exhibir una eficiencia estadística dramáticamente mayor si el espacio de estado no está restringido.
Esto significa que tendremos que resolver dos problemas principales al tomar muestras del BGMM posterior:
- \(\theta\) representa un vector de probabilidad discreta, es decir, debe ser tal que \(\sum_{k=1}^K \theta_k = 1\) y \(\theta_k>0\).
- \(T_k\) representa un inverso de covarianza matriz, es decir, debe ser tal que \(T_k \succ 0\), es decir, es definida positiva .
Para abordar este requisito, necesitaremos:
- transformar las variables restringidas en un espacio no restringido
- ejecutar la MCMC en un espacio sin restricciones
- transformar las variables no restringidas de nuevo al espacio restringido.
Al igual que con MVNCholPrecisionTriL , usaremos Bijector s para transformar variables aleatorias al espacio sin restricciones.
El
Dirichletse transforma en el espacio sin restricciones a través de la función de softmax .Nuestra variable aleatoria de precisión es una distribución sobre matrices semidefinidas positivas. Para el forzado estos usaremos los
FillTriangularyTransformDiagonalbijectors. Estos convierten vectores en matrices triangulares inferiores y aseguran que la diagonal sea positiva. El primero es útil porque permite el muestreo solamente \(d(d+1)/2\) flota en lugar de \(d^2\).
unconstraining_bijectors = [
tfb.SoftmaxCentered(),
tfb.Identity(),
tfb.Chain([
tfb.TransformDiagonal(tfb.Softplus()),
tfb.FillTriangular(),
])]
@tf.function(autograph=False)
def sample():
return tfp.mcmc.sample_chain(
num_results=2000,
num_burnin_steps=500,
current_state=initial_state,
kernel=tfp.mcmc.SimpleStepSizeAdaptation(
tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unnormalized_posterior_log_prob,
step_size=0.065,
num_leapfrog_steps=5),
bijector=unconstraining_bijectors),
num_adaptation_steps=400),
trace_fn=lambda _, pkr: pkr.inner_results.inner_results.is_accepted)
[mix_probs, loc, chol_precision], is_accepted = sample()
Ahora ejecutaremos la cadena e imprimiremos las medias posteriores.
acceptance_rate = tf.reduce_mean(tf.cast(is_accepted, dtype=tf.float32)).numpy()
mean_mix_probs = tf.reduce_mean(mix_probs, axis=0).numpy()
mean_loc = tf.reduce_mean(loc, axis=0).numpy()
mean_chol_precision = tf.reduce_mean(chol_precision, axis=0).numpy()
precision = tf.linalg.matmul(chol_precision, chol_precision, transpose_b=True)
print('acceptance_rate:', acceptance_rate)
print('avg mix probs:', mean_mix_probs)
print('avg loc:\n', mean_loc)
print('avg chol(precision):\n', mean_chol_precision)
acceptance_rate: 0.5305 avg mix probs: [0.25248723 0.60729516 0.1402176 ] avg loc: [[-1.96466753 -2.12047249] [ 0.27628865 0.22944732] [ 2.06461244 2.54216122]] avg chol(precision): [[[ 1.05105032 0. ] [ 0.12699955 1.06553113]] [[ 0.76058015 0. ] [-0.50332767 0.77947431]] [[ 1.22770457 0. ] [ 0.70670027 1.50914164]]]
loc_ = loc.numpy()
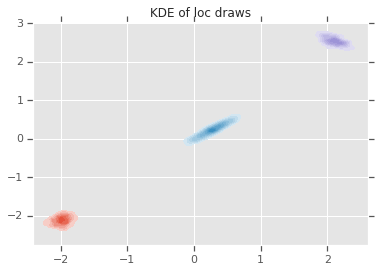
ax = sns.kdeplot(loc_[:,0,0], loc_[:,0,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,1,0], loc_[:,1,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,2,0], loc_[:,2,1], shade=True, shade_lowest=False)
plt.title('KDE of loc draws');
Conclusión
Esta sencilla colaboración demostró cómo se pueden usar las primitivas de probabilidad de TensorFlow para crear modelos de mezcla bayesianos jerárquicos.
