 TensorFlow.org で表示 TensorFlow.org で表示 |
 Google Colab で実行 Google Colab で実行 |
 GitHub でソースを表示 GitHub でソースを表示 |
 ノートブックをダウンロード ノートブックをダウンロード |
確率的主成分分析(PCA)は、低次元の潜在空間を介してデータを分析する次元削減手法です(Tipping and Bishop 1999)。データの値が欠落している場合や多次元スケーリングに多く使用されます。
インポート
import functools
import warnings
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
モデル
\(N\) データポイントのデータセット \(\mathbf{X} = {\mathbf{x}_n}\) を検討します。各データポイントは \(D\)-dimensional, \(\mathbf{x}_n \in \mathbb{R}^D\) です。低次元 \(K < D\) で、潜在変数 \(\mathbf{z}_n \in \mathbb{R}^K\) で各 \(\mathbf{x}_n\) を表現したいと思います。主軸 \(\mathbf{W}\) のセットは、潜在変数をデータに関連付けます。
具体的には、各潜在変数は正規に分布されていると仮定します。
\[ \begin{equation*} \mathbf{z}_n \sim N(\mathbf{0}, \mathbf{I}). \end{equation*} \]
対応するデータポイントは、プロジェクションを介して生成されます。
\[ \begin{equation*} \mathbf{x}_n \mid \mathbf{z}_n \sim N(\mathbf{W}\mathbf{z}_n, \sigma^2\mathbf{I}), \end{equation*} \]
上記の行列 \(\mathbf{W}\in\mathbb{R}^{D\times K}\) は主軸として知られています。確率的 PCA では通常、主軸 \(\mathbf{W}\) とノイズ項 \(\sigma^2\) の推定に関心があります。
確率的 PCA は、古典的な PCA を一般化したものです。潜在変数を除外した場合、各データポイントの分布は、次のようになります。
\[ \begin{equation*} \mathbf{x}_n \sim N(\mathbf{0}, \mathbf{W}\mathbf{W}^\top + \sigma^2\mathbf{I}). \end{equation*} \]
古典的な PCA は、ノイズの共分散が \(\sigma^2 \to 0\) のように非常に小さくなる確率的 PCA 特有のケースです。
モデルを以下のようにセットアップしました。この分析では、\(\sigma\) が既知であると想定しており、\(\mathbf{W}\) をモデルパラメータとして想定しているポイントの代わりに、主軸に対する分布を推論するために事前分布をかぶせています。このモデルを TFP JointDistribution として表現し、具体的に、JointDistributionCoroutineAutoBatched を使用します。
def probabilistic_pca(data_dim, latent_dim, num_datapoints, stddv_datapoints):
w = yield tfd.Normal(loc=tf.zeros([data_dim, latent_dim]),
scale=2.0 * tf.ones([data_dim, latent_dim]),
name="w")
z = yield tfd.Normal(loc=tf.zeros([latent_dim, num_datapoints]),
scale=tf.ones([latent_dim, num_datapoints]),
name="z")
x = yield tfd.Normal(loc=tf.matmul(w, z),
scale=stddv_datapoints,
name="x")
num_datapoints = 5000
data_dim = 2
latent_dim = 1
stddv_datapoints = 0.5
concrete_ppca_model = functools.partial(probabilistic_pca,
data_dim=data_dim,
latent_dim=latent_dim,
num_datapoints=num_datapoints,
stddv_datapoints=stddv_datapoints)
model = tfd.JointDistributionCoroutineAutoBatched(concrete_ppca_model)
データ
このモデルを使用し、同時事前分布からサンプリングしてデータを生成することができます。
actual_w, actual_z, x_train = model.sample()
print("Principal axes:")
print(actual_w)
Principal axes: tf.Tensor( [[ 2.2801023] [-1.1619819]], shape=(2, 1), dtype=float32)
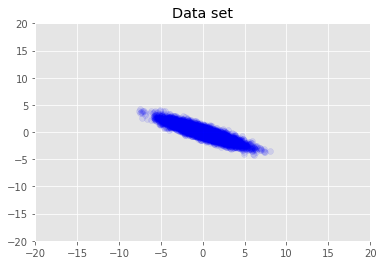
データセットを視覚化します。
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1)
plt.axis([-20, 20, -20, 20])
plt.title("Data set")
plt.show()
最大事後確率推定
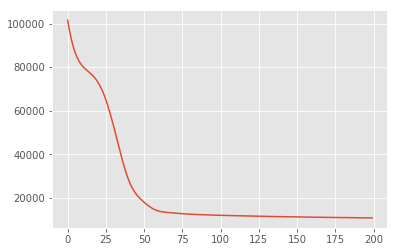
まず、事後確率密度を最大化する潜在変数の点推定を探します。これは、最大事後確率(MAP)推定法として知られており、事後確率密度 \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}) \propto p(\mathbf{W}, \mathbf{Z}, \mathbf{X})\) を最大化する \(\mathbf{W}\) と \(\mathbf{Z}\) の値を計算することで行われます。
w = tf.Variable(tf.random.normal([data_dim, latent_dim]))
z = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
target_log_prob_fn = lambda w, z: model.log_prob((w, z, x_train))
losses = tfp.math.minimize(
lambda: -target_log_prob_fn(w, z),
optimizer=tf.optimizers.Adam(learning_rate=0.05),
num_steps=200)
plt.plot(losses)
[<matplotlib.lines.Line2D at 0x7f19897a42e8>]
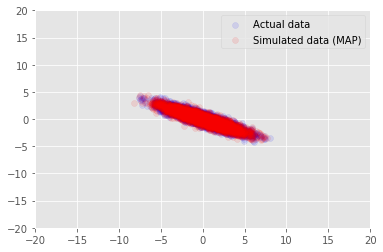
モデルを使用して、\(\mathbf{W}\) と \(\mathbf{Z}\) の推定値を得るデータをサンプリングし、条件を設定した実際のデータセットと比較します。
print("MAP-estimated axes:")
print(w)
_, _, x_generated = model.sample(value=(w, z, None))
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (MAP)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()
MAP-estimated axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.9135954],
[-1.4826864]], dtype=float32)>
変分推論
MAP は、事後分布のモード(またはモードの 1 つ)を見つけるために使用できますが、それに関するインサイトは何も提供しません。次に、変分推論を使用してみましょう。事後分布 \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X})\) は \(\boldsymbol{\lambda}\) でパラメーター化された変分分布 \(q(\mathbf{W}, \mathbf{Z})\) を使用して概算されます。q と事後分布の KL 発散を最小化する変分パラメーター \(\boldsymbol{\lambda}\) を見つけること(\(\mathrm{KL}(q(\mathbf{W}, \mathbf{Z}) \mid\mid p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}))\))または同様に、根拠の下限を最大化する変分パラメーター \(\boldsymbol{\lambda}\) を見つけること(\(\mathbb{E}_{q(\mathbf{W},\mathbf{Z};\boldsymbol{\lambda})}\left[ \log p(\mathbf{W},\mathbf{Z},\mathbf{X}) - \log q(\mathbf{W},\mathbf{Z}; \boldsymbol{\lambda}) \right]\))を目標とします。
qw_mean = tf.Variable(tf.random.normal([data_dim, latent_dim]))
qz_mean = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
qw_stddv = tfp.util.TransformedVariable(1e-4 * tf.ones([data_dim, latent_dim]),
bijector=tfb.Softplus())
qz_stddv = tfp.util.TransformedVariable(
1e-4 * tf.ones([latent_dim, num_datapoints]),
bijector=tfb.Softplus())
def factored_normal_variational_model():
qw = yield tfd.Normal(loc=qw_mean, scale=qw_stddv, name="qw")
qz = yield tfd.Normal(loc=qz_mean, scale=qz_stddv, name="qz")
surrogate_posterior = tfd.JointDistributionCoroutineAutoBatched(
factored_normal_variational_model)
losses = tfp.vi.fit_surrogate_posterior(
target_log_prob_fn,
surrogate_posterior=surrogate_posterior,
optimizer=tf.optimizers.Adam(learning_rate=0.05),
num_steps=200)
print("Inferred axes:")
print(qw_mean)
print("Standard Deviation:")
print(qw_stddv)
plt.plot(losses)
plt.show()
Inferred axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.4168603],
[-1.2236133]], dtype=float32)>
Standard Deviation:
<TransformedVariable: dtype=float32, shape=[2, 1], fn="softplus", numpy=
array([[0.0042499 ],
[0.00598824]], dtype=float32)>
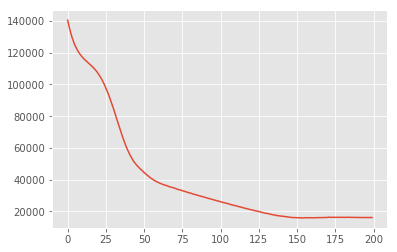
posterior_samples = surrogate_posterior.sample(50)
_, _, x_generated = model.sample(value=(posterior_samples))
# It's a pain to plot all 5000 points for each of our 50 posterior samples, so
# let's subsample to get the gist of the distribution.
x_generated = tf.reshape(tf.transpose(x_generated, [1, 0, 2]), (2, -1))[:, ::47]
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (VI)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()
謝辞
このチュートリアルは Edward 1.0 (出典) に掲載されたものです。そのバージョンの作成と改訂に貢献されたすべての人に感謝します。
参照文献
[1]: Michael E. Tipping and Christopher M. Bishop. Probabilistic principal component analysis. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 61(3): 611-622, 1999.
