 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Ce didacticiel explore les algorithmes de calcul de gradient pour les valeurs d'attente des circuits quantiques.
Le calcul du gradient de la valeur d'attente d'un certain observable dans un circuit quantique est un processus complexe. Les valeurs d'attente des observables n'ont pas le luxe d'avoir des formules de gradient analytique qui sont toujours faciles à écrire, contrairement aux transformations d'apprentissage automatique traditionnelles telles que la multiplication matricielle ou l'addition de vecteurs qui ont des formules de gradient analytique faciles à écrire. En conséquence, il existe différentes méthodes de calcul du gradient quantique qui sont utiles pour différents scénarios. Ce didacticiel compare et oppose deux schémas de différenciation différents.
Installer
pip install tensorflow==2.7.0
Installez TensorFlow Quantum :
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Importez maintenant TensorFlow et les dépendances du module :
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:25:24.733670: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Préliminaire
Rendons un peu plus concrète la notion de calcul de gradient pour les circuits quantiques. Supposons que vous ayez un circuit paramétré comme celui-ci :
qubit = cirq.GridQubit(0, 0)
my_circuit = cirq.Circuit(cirq.Y(qubit)**sympy.Symbol('alpha'))
SVGCircuit(my_circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Accompagné d'un observable :
pauli_x = cirq.X(qubit)
pauli_x
cirq.X(cirq.GridQubit(0, 0))
En regardant cet opérateur, vous savez que \(⟨Y(\alpha)| X | Y(\alpha)⟩ = \sin(\pi \alpha)\)
def my_expectation(op, alpha):
"""Compute ⟨Y(alpha)| `op` | Y(alpha)⟩"""
params = {'alpha': alpha}
sim = cirq.Simulator()
final_state_vector = sim.simulate(my_circuit, params).final_state_vector
return op.expectation_from_state_vector(final_state_vector, {qubit: 0}).real
my_alpha = 0.3
print("Expectation=", my_expectation(pauli_x, my_alpha))
print("Sin Formula=", np.sin(np.pi * my_alpha))
Expectation= 0.80901700258255 Sin Formula= 0.8090169943749475
et si vous définissez \(f_{1}(\alpha) = ⟨Y(\alpha)| X | Y(\alpha)⟩\) puis \(f_{1}^{'}(\alpha) = \pi \cos(\pi \alpha)\). Vérifions ceci :
def my_grad(obs, alpha, eps=0.01):
grad = 0
f_x = my_expectation(obs, alpha)
f_x_prime = my_expectation(obs, alpha + eps)
return ((f_x_prime - f_x) / eps).real
print('Finite difference:', my_grad(pauli_x, my_alpha))
print('Cosine formula: ', np.pi * np.cos(np.pi * my_alpha))
Finite difference: 1.8063604831695557 Cosine formula: 1.8465818304904567
2. La nécessité d'un différenciateur
Avec des circuits plus grands, vous n'aurez pas toujours la chance d'avoir une formule qui calcule précisément les gradients d'un circuit quantique donné. Dans le cas où une simple formule ne suffirait pas à calculer le gradient, la classe tfq.differentiators.Differentiator permet de définir des algorithmes de calcul des gradients de vos circuits. Par exemple, vous pouvez recréer l'exemple ci-dessus dans TensorFlow Quantum (TFQ) avec :
expectation_calculation = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.80901706]], dtype=float32)>
Cependant, si vous passez à l'estimation de l'attente basée sur l'échantillonnage (ce qui se passerait sur un véritable appareil), les valeurs peuvent changer un peu. Cela signifie que vous avez maintenant une estimation imparfaite :
sampled_expectation_calculation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=[[my_alpha]])
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.836]], dtype=float32)>
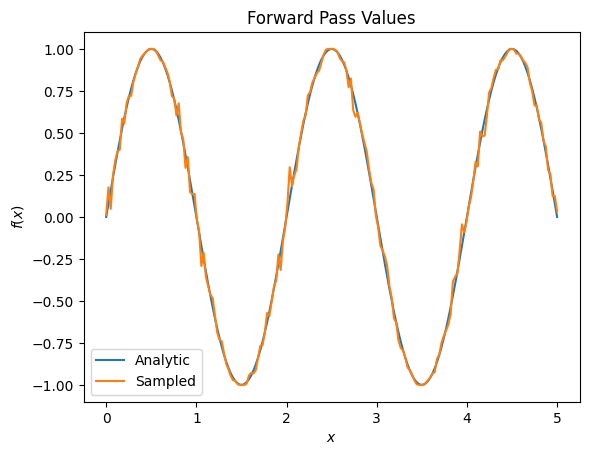
Cela peut rapidement aggraver un sérieux problème de précision en ce qui concerne les gradients :
# Make input_points = [batch_size, 1] array.
input_points = np.linspace(0, 5, 200)[:, np.newaxis].astype(np.float32)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=input_points)
imperfect_outputs = sampled_expectation_calculation(my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=input_points)
plt.title('Forward Pass Values')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.plot(input_points, exact_outputs, label='Analytic')
plt.plot(input_points, imperfect_outputs, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07d556190>
# Gradients are a much different story.
values_tensor = tf.convert_to_tensor(input_points)
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=pauli_x,
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = sampled_expectation_calculation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_finite_diff_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_finite_diff_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07adb8dd0>
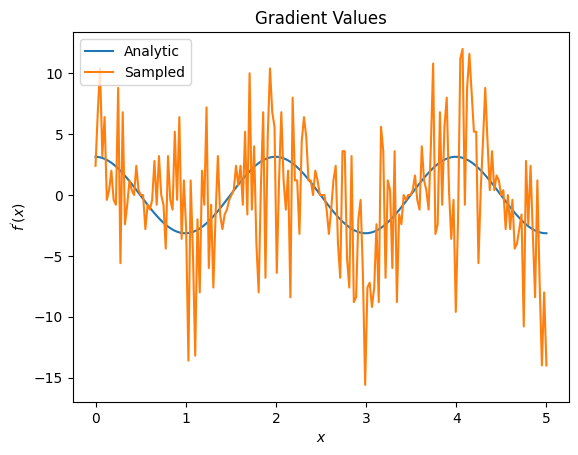
Ici, vous pouvez voir que bien que la formule de différence finie soit rapide pour calculer les gradients eux-mêmes dans le cas analytique, en ce qui concerne les méthodes basées sur l'échantillonnage, elle était beaucoup trop bruyante. Des techniques plus prudentes doivent être utilisées pour s'assurer qu'un bon gradient peut être calculé. Ensuite, vous examinerez une technique beaucoup plus lente qui ne serait pas aussi bien adaptée aux calculs de gradient d'attente analytique, mais qui fonctionne bien mieux dans le cas réel basé sur un échantillon :
# A smarter differentiation scheme.
gradient_safe_sampled_expectation = tfq.layers.SampledExpectation(
differentiator=tfq.differentiators.ParameterShift())
with tf.GradientTape() as g:
g.watch(values_tensor)
imperfect_outputs = gradient_safe_sampled_expectation(
my_circuit,
operators=pauli_x,
repetitions=500,
symbol_names=['alpha'],
symbol_values=values_tensor)
sampled_param_shift_gradients = g.gradient(imperfect_outputs, values_tensor)
plt.title('Gradient Values')
plt.xlabel('$x$')
plt.ylabel('$f^{\'}(x)$')
plt.plot(input_points, analytic_finite_diff_gradients, label='Analytic')
plt.plot(input_points, sampled_param_shift_gradients, label='Sampled')
plt.legend()
<matplotlib.legend.Legend at 0x7ff07ad9ff90>
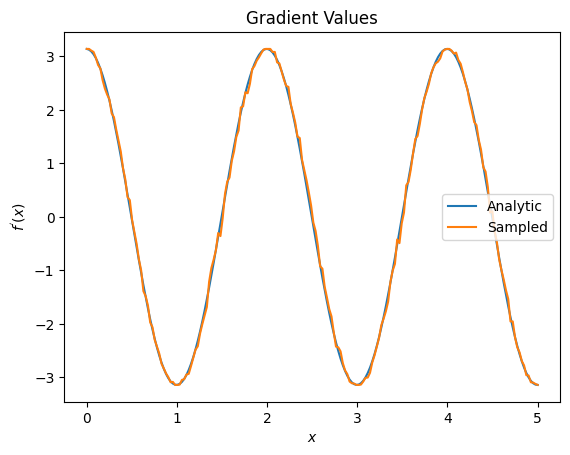
D'après ce qui précède, vous pouvez voir que certains différenciateurs sont mieux utilisés pour des scénarios de recherche particuliers. En général, les méthodes basées sur des échantillons plus lentes qui sont robustes au bruit de l'appareil, etc., sont d'excellents différenciateurs lors du test ou de la mise en œuvre d'algorithmes dans un cadre plus "réel". Les méthodes plus rapides comme la différence finie sont idéales pour les calculs analytiques et vous souhaitez un débit plus élevé, mais vous n'êtes pas encore concerné par la viabilité de l'appareil de votre algorithme.
3. Plusieurs observables
Introduisons un deuxième observable et voyons comment TensorFlow Quantum prend en charge plusieurs observables pour un seul circuit.
pauli_z = cirq.Z(qubit)
pauli_z
cirq.Z(cirq.GridQubit(0, 0))
Si cet observable est utilisé avec le même circuit qu'avant, alors vous avez \(f_{2}(\alpha) = ⟨Y(\alpha)| Z | Y(\alpha)⟩ = \cos(\pi \alpha)\) et \(f_{2}^{'}(\alpha) = -\pi \sin(\pi \alpha)\). Effectuez une vérification rapide :
test_value = 0.
print('Finite difference:', my_grad(pauli_z, test_value))
print('Sin formula: ', -np.pi * np.sin(np.pi * test_value))
Finite difference: -0.04934072494506836 Sin formula: -0.0
C'est un match (assez proche).
Maintenant, si vous définissez \(g(\alpha) = f_{1}(\alpha) + f_{2}(\alpha)\) puis \(g'(\alpha) = f_{1}^{'}(\alpha) + f^{'}_{2}(\alpha)\). Définir plusieurs observables dans TensorFlow Quantum à utiliser avec un circuit équivaut à ajouter plusieurs termes à \(g\).
Cela signifie que le gradient d'un symbole particulier dans un circuit est égal à la somme des gradients par rapport à chaque observable pour ce symbole appliqué à ce circuit. Ceci est compatible avec la prise de gradient et la rétropropagation de TensorFlow (où vous donnez la somme des gradients sur tous les observables comme gradient pour un symbole particulier).
sum_of_outputs = tfq.layers.Expectation(
differentiator=tfq.differentiators.ForwardDifference(grid_spacing=0.01))
sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=[[test_value]])
<tf.Tensor: shape=(1, 2), dtype=float32, numpy=array([[1.9106855e-15, 1.0000000e+00]], dtype=float32)>
Ici, vous voyez que la première entrée est l'espérance par rapport à Pauli X, et la seconde est l'espérance par rapport à Pauli Z. Maintenant, quand vous prenez le gradient :
test_value_tensor = tf.convert_to_tensor([[test_value]])
with tf.GradientTape() as g:
g.watch(test_value_tensor)
outputs = sum_of_outputs(my_circuit,
operators=[pauli_x, pauli_z],
symbol_names=['alpha'],
symbol_values=test_value_tensor)
sum_of_gradients = g.gradient(outputs, test_value_tensor)
print(my_grad(pauli_x, test_value) + my_grad(pauli_z, test_value))
print(sum_of_gradients.numpy())
3.0917350202798843 [[3.0917213]]
Ici vous avez vérifié que la somme des gradients pour chaque observable est bien le gradient de \(\alpha\). Ce comportement est pris en charge par tous les différenciateurs TensorFlow Quantum et joue un rôle crucial dans la compatibilité avec le reste de TensorFlow.
4. Utilisation avancée
Tous les différenciateurs qui existent à l'intérieur de la sous-classe TensorFlow Quantum tfq.differentiators.Differentiator . Pour implémenter un différenciateur, un utilisateur doit implémenter l'une des deux interfaces. La norme consiste à implémenter get_gradient_circuits , qui indique à la classe de base quels circuits mesurer pour obtenir une estimation du gradient. Alternativement, vous pouvez surcharger differentiate_analytic et differentiate_sampled ; la classe tfq.differentiators.Adjoint emprunte cette route.
Ce qui suit utilise TensorFlow Quantum pour implémenter le gradient d'un circuit. Vous utiliserez un petit exemple de décalage de paramètre.
Rappelez-vous le circuit que vous avez défini ci-dessus, \(|\alpha⟩ = Y^{\alpha}|0⟩\). Comme précédemment, vous pouvez définir une fonction comme valeur d'attente de ce circuit par rapport à l'observable \(X\) , \(f(\alpha) = ⟨\alpha|X|\alpha⟩\). En utilisant les règles de décalage des paramètres , pour ce circuit, vous pouvez trouver que la dérivée est
\[\frac{\partial}{\partial \alpha} f(\alpha) = \frac{\pi}{2} f\left(\alpha + \frac{1}{2}\right) - \frac{ \pi}{2} f\left(\alpha - \frac{1}{2}\right)\]
La fonction get_gradient_circuits renvoie les composantes de cette dérivée.
class MyDifferentiator(tfq.differentiators.Differentiator):
"""A Toy differentiator for <Y^alpha | X |Y^alpha>."""
def __init__(self):
pass
def get_gradient_circuits(self, programs, symbol_names, symbol_values):
"""Return circuits to compute gradients for given forward pass circuits.
Every gradient on a quantum computer can be computed via measurements
of transformed quantum circuits. Here, you implement a custom gradient
for a specific circuit. For a real differentiator, you will need to
implement this function in a more general way. See the differentiator
implementations in the TFQ library for examples.
"""
# The two terms in the derivative are the same circuit...
batch_programs = tf.stack([programs, programs], axis=1)
# ... with shifted parameter values.
shift = tf.constant(1/2)
forward = symbol_values + shift
backward = symbol_values - shift
batch_symbol_values = tf.stack([forward, backward], axis=1)
# Weights are the coefficients of the terms in the derivative.
num_program_copies = tf.shape(batch_programs)[0]
batch_weights = tf.tile(tf.constant([[[np.pi/2, -np.pi/2]]]),
[num_program_copies, 1, 1])
# The index map simply says which weights go with which circuits.
batch_mapper = tf.tile(
tf.constant([[[0, 1]]]), [num_program_copies, 1, 1])
return (batch_programs, symbol_names, batch_symbol_values,
batch_weights, batch_mapper)
La classe de base Differentiator utilise les composants renvoyés par get_gradient_circuits pour calculer la dérivée, comme dans la formule de décalage de paramètre que vous avez vue ci-dessus. Ce nouveau différenciateur peut désormais être utilisé avec les objets tfq.layer existants :
custom_dif = MyDifferentiator()
custom_grad_expectation = tfq.layers.Expectation(differentiator=custom_dif)
# Now let's get the gradients with finite diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
exact_outputs = expectation_calculation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
analytic_finite_diff_gradients = g.gradient(exact_outputs, values_tensor)
# Now let's get the gradients with custom diff.
with tf.GradientTape() as g:
g.watch(values_tensor)
my_outputs = custom_grad_expectation(my_circuit,
operators=[pauli_x],
symbol_names=['alpha'],
symbol_values=values_tensor)
my_gradients = g.gradient(my_outputs, values_tensor)
plt.subplot(1, 2, 1)
plt.title('Exact Gradient')
plt.plot(input_points, analytic_finite_diff_gradients.numpy())
plt.xlabel('x')
plt.ylabel('f(x)')
plt.subplot(1, 2, 2)
plt.title('My Gradient')
plt.plot(input_points, my_gradients.numpy())
plt.xlabel('x')
Text(0.5, 0, 'x')
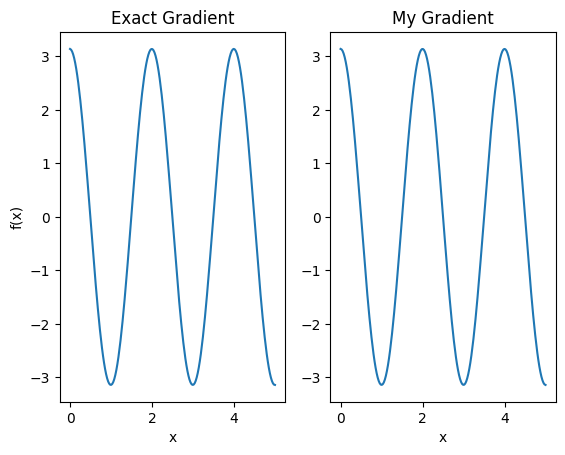
Ce nouveau différenciateur peut maintenant être utilisé pour générer des opérations différenciables.
# Create a noisy sample based expectation op.
expectation_sampled = tfq.get_sampled_expectation_op(
cirq.DensityMatrixSimulator(noise=cirq.depolarize(0.01)))
# Make it differentiable with your differentiator:
# Remember to refresh the differentiator before attaching the new op
custom_dif.refresh()
differentiable_op = custom_dif.generate_differentiable_op(
sampled_op=expectation_sampled)
# Prep op inputs.
circuit_tensor = tfq.convert_to_tensor([my_circuit])
op_tensor = tfq.convert_to_tensor([[pauli_x]])
single_value = tf.convert_to_tensor([[my_alpha]])
num_samples_tensor = tf.convert_to_tensor([[5000]])
with tf.GradientTape() as g:
g.watch(single_value)
forward_output = differentiable_op(circuit_tensor, ['alpha'], single_value,
op_tensor, num_samples_tensor)
my_gradients = g.gradient(forward_output, single_value)
print('---TFQ---')
print('Foward: ', forward_output.numpy())
print('Gradient:', my_gradients.numpy())
print('---Original---')
print('Forward: ', my_expectation(pauli_x, my_alpha))
print('Gradient:', my_grad(pauli_x, my_alpha))
---TFQ--- Foward: [[0.8016]] Gradient: [[1.7932211]] ---Original--- Forward: 0.80901700258255 Gradient: 1.8063604831695557
