 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
Construido a partir de las comparaciones realizadas en el MNIST tutorial, este tutorial explora el reciente trabajo de Huang et al. que muestra cómo los diferentes conjuntos de datos afectan las comparaciones de rendimiento. En el trabajo, los autores buscan comprender cómo y cuándo los modelos clásicos de aprendizaje automático pueden aprender tan bien como (o mejor que) los modelos cuánticos. El trabajo también muestra una separación de rendimiento empírico entre el modelo de aprendizaje automático clásico y cuántico a través de un conjunto de datos cuidadosamente elaborado. Vas a:
- Prepare un conjunto de datos Fashion-MNIST de dimensión reducida.
- Utilice circuitos cuánticos para volver a etiquetar el conjunto de datos y calcular las características del núcleo cuántico proyectado (PQK).
- Entrene una red neuronal clásica en el conjunto de datos reetiquetado y compare el rendimiento con un modelo que tenga acceso a las funciones de PQK.
Configuración
pip install tensorflow==2.4.1 tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
import cirq
import sympy
import numpy as np
import tensorflow as tf
import tensorflow_quantum as tfq
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
np.random.seed(1234)
1. Preparación de datos
Comenzará por preparar el conjunto de datos fashion-MNIST para ejecutarlo en una computadora cuántica.
1.1 Descargar fashion-MNIST
El primer paso es obtener el conjunto de datos de moda tradicional. Esto se puede hacer mediante el tf.keras.datasets módulo.
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
# Rescale the images from [0,255] to the [0.0,1.0] range.
x_train, x_test = x_train/255.0, x_test/255.0
print("Number of original training examples:", len(x_train))
print("Number of original test examples:", len(x_test))
Number of original training examples: 60000 Number of original test examples: 10000
Filtre el conjunto de datos para mantener solo las camisetas / tops y vestidos, elimine las otras clases. Al mismo tiempo convertir la etiqueta, y , a booleano: true para 0 y False para 3.
def filter_03(x, y):
keep = (y == 0) | (y == 3)
x, y = x[keep], y[keep]
y = y == 0
return x,y
x_train, y_train = filter_03(x_train, y_train)
x_test, y_test = filter_03(x_test, y_test)
print("Number of filtered training examples:", len(x_train))
print("Number of filtered test examples:", len(x_test))
Number of filtered training examples: 12000 Number of filtered test examples: 2000
print(y_train[0])
plt.imshow(x_train[0, :, :])
plt.colorbar()
True <matplotlib.colorbar.Colorbar at 0x7f6db42c3460>

1.2 Reducir la escala de las imágenes
Al igual que en el ejemplo de MNIST, deberá reducir la escala de estas imágenes para estar dentro de los límites de las computadoras cuánticas actuales. Esta vez, sin embargo se utilizará una transformación PCA para reducir las dimensiones en lugar de un tf.image.resize operación.
def truncate_x(x_train, x_test, n_components=10):
"""Perform PCA on image dataset keeping the top `n_components` components."""
n_points_train = tf.gather(tf.shape(x_train), 0)
n_points_test = tf.gather(tf.shape(x_test), 0)
# Flatten to 1D
x_train = tf.reshape(x_train, [n_points_train, -1])
x_test = tf.reshape(x_test, [n_points_test, -1])
# Normalize.
feature_mean = tf.reduce_mean(x_train, axis=0)
x_train_normalized = x_train - feature_mean
x_test_normalized = x_test - feature_mean
# Truncate.
e_values, e_vectors = tf.linalg.eigh(
tf.einsum('ji,jk->ik', x_train_normalized, x_train_normalized))
return tf.einsum('ij,jk->ik', x_train_normalized, e_vectors[:,-n_components:]), \
tf.einsum('ij,jk->ik', x_test_normalized, e_vectors[:, -n_components:])
DATASET_DIM = 10
x_train, x_test = truncate_x(x_train, x_test, n_components=DATASET_DIM)
print(f'New datapoint dimension:', len(x_train[0]))
New datapoint dimension: 10
El último paso es reducir el tamaño del conjunto de datos a solo 1000 puntos de datos de entrenamiento y 200 puntos de datos de prueba.
N_TRAIN = 1000
N_TEST = 200
x_train, x_test = x_train[:N_TRAIN], x_test[:N_TEST]
y_train, y_test = y_train[:N_TRAIN], y_test[:N_TEST]
print("New number of training examples:", len(x_train))
print("New number of test examples:", len(x_test))
New number of training examples: 1000 New number of test examples: 200
2. Reetiquetado y cálculo de funciones de PQK
Ahora preparará un conjunto de datos cuánticos "estructurado" incorporando componentes cuánticos y volviendo a etiquetar el conjunto de datos de moda-MNIST truncado que ha creado anteriormente. Para obtener la mayor separación entre los métodos cuántico y clásico, primero preparará las características de PQK y luego volverá a etiquetar las salidas en función de sus valores.
2.1 Codificación cuántica y funciones PQK
Va a crear un nuevo conjunto de características, basado en x_train , y_train , x_test y y_test que se define como el 1-RDM en todos los qubits de:
\(V(x_{\text{train} } / n_{\text{trotter} }) ^ {n_{\text{trotter} } } U_{\text{1qb} } | 0 \rangle\)
Donde \(U_\text{1qb}\) es una pared de rotaciones qubits individuales y \(V(\hat{\theta}) = e^{-i\sum_i \hat{\theta_i} (X_i X_{i+1} + Y_i Y_{i+1} + Z_i Z_{i+1})}\)
Primero, puede generar la pared de rotaciones de un solo qubit:
def single_qubit_wall(qubits, rotations):
"""Prepare a single qubit X,Y,Z rotation wall on `qubits`."""
wall_circuit = cirq.Circuit()
for i, qubit in enumerate(qubits):
for j, gate in enumerate([cirq.X, cirq.Y, cirq.Z]):
wall_circuit.append(gate(qubit) ** rotations[i][j])
return wall_circuit
Puede verificar rápidamente que esto funciona mirando el circuito:
SVGCircuit(single_qubit_wall(
cirq.GridQubit.rect(1,4), np.random.uniform(size=(4, 3))))
A continuación se puede preparar \(V(\hat{\theta})\) con la ayuda de tfq.util.exponential que puede exponenciar cualquier trayecto cirq.PauliSum objetos:
def v_theta(qubits):
"""Prepares a circuit that generates V(\theta)."""
ref_paulis = [
cirq.X(q0) * cirq.X(q1) + \
cirq.Y(q0) * cirq.Y(q1) + \
cirq.Z(q0) * cirq.Z(q1) for q0, q1 in zip(qubits, qubits[1:])
]
exp_symbols = list(sympy.symbols('ref_0:'+str(len(ref_paulis))))
return tfq.util.exponential(ref_paulis, exp_symbols), exp_symbols
Este circuito puede ser un poco más difícil de verificar al mirar, pero aún puede examinar un caso de dos qubit para ver qué está sucediendo:
test_circuit, test_symbols = v_theta(cirq.GridQubit.rect(1, 2))
print(f'Symbols found in circuit:{test_symbols}')
SVGCircuit(test_circuit)
Symbols found in circuit:[ref_0]
Ahora tiene todos los componentes básicos que necesita para unir todos sus circuitos de codificación:
def prepare_pqk_circuits(qubits, classical_source, n_trotter=10):
"""Prepare the pqk feature circuits around a dataset."""
n_qubits = len(qubits)
n_points = len(classical_source)
# Prepare random single qubit rotation wall.
random_rots = np.random.uniform(-2, 2, size=(n_qubits, 3))
initial_U = single_qubit_wall(qubits, random_rots)
# Prepare parametrized V
V_circuit, symbols = v_theta(qubits)
exp_circuit = cirq.Circuit(V_circuit for t in range(n_trotter))
# Convert to `tf.Tensor`
initial_U_tensor = tfq.convert_to_tensor([initial_U])
initial_U_splat = tf.tile(initial_U_tensor, [n_points])
full_circuits = tfq.layers.AddCircuit()(
initial_U_splat, append=exp_circuit)
# Replace placeholders in circuits with values from `classical_source`.
return tfq.resolve_parameters(
full_circuits, tf.convert_to_tensor([str(x) for x in symbols]),
tf.convert_to_tensor(classical_source*(n_qubits/3)/n_trotter))
Elija algunos qubits y prepare los circuitos de codificación de datos:
qubits = cirq.GridQubit.rect(1, DATASET_DIM + 1)
q_x_train_circuits = prepare_pqk_circuits(qubits, x_train)
q_x_test_circuits = prepare_pqk_circuits(qubits, x_test)
A continuación, calcular el PQK características basadas en el 1-RDM de los circuitos del conjunto de datos anteriores y almacenar los resultados en rdm , un tf.Tensor con forma [n_points, n_qubits, 3] . Las entradas en rdm[i][j][k] = \(\langle \psi_i | OP^k_j | \psi_i \rangle\) donde i índices más puntos de datos, j índices más de qubits y k índices más \(\lbrace \hat{X}, \hat{Y}, \hat{Z} \rbrace\) .
def get_pqk_features(qubits, data_batch):
"""Get PQK features based on above construction."""
ops = [[cirq.X(q), cirq.Y(q), cirq.Z(q)] for q in qubits]
ops_tensor = tf.expand_dims(tf.reshape(tfq.convert_to_tensor(ops), -1), 0)
batch_dim = tf.gather(tf.shape(data_batch), 0)
ops_splat = tf.tile(ops_tensor, [batch_dim, 1])
exp_vals = tfq.layers.Expectation()(data_batch, operators=ops_splat)
rdm = tf.reshape(exp_vals, [batch_dim, len(qubits), -1])
return rdm
x_train_pqk = get_pqk_features(qubits, q_x_train_circuits)
x_test_pqk = get_pqk_features(qubits, q_x_test_circuits)
print('New PQK training dataset has shape:', x_train_pqk.shape)
print('New PQK testing dataset has shape:', x_test_pqk.shape)
New PQK training dataset has shape: (1000, 11, 3) New PQK testing dataset has shape: (200, 11, 3)
2.2 Reetiquetado basado en características PQK
Ahora que tiene estas características cuánticas generado en x_train_pqk y x_test_pqk , es el momento de volver a etiquetar el conjunto de datos. Para conseguir la máxima separación entre cuántica y el rendimiento clásica puede volver a etiquetar el conjunto de datos basado en la información que se encuentra en el espectro x_train_pqk y x_test_pqk .
def compute_kernel_matrix(vecs, gamma):
"""Computes d[i][j] = e^ -gamma * (vecs[i] - vecs[j]) ** 2 """
scaled_gamma = gamma / (
tf.cast(tf.gather(tf.shape(vecs), 1), tf.float32) * tf.math.reduce_std(vecs))
return scaled_gamma * tf.einsum('ijk->ij',(vecs[:,None,:] - vecs) ** 2)
def get_spectrum(datapoints, gamma=1.0):
"""Compute the eigenvalues and eigenvectors of the kernel of datapoints."""
KC_qs = compute_kernel_matrix(datapoints, gamma)
S, V = tf.linalg.eigh(KC_qs)
S = tf.math.abs(S)
return S, V
S_pqk, V_pqk = get_spectrum(
tf.reshape(tf.concat([x_train_pqk, x_test_pqk], 0), [-1, len(qubits) * 3]))
S_original, V_original = get_spectrum(
tf.cast(tf.concat([x_train, x_test], 0), tf.float32), gamma=0.005)
print('Eigenvectors of pqk kernel matrix:', V_pqk)
print('Eigenvectors of original kernel matrix:', V_original)
Eigenvectors of pqk kernel matrix: tf.Tensor( [[-2.09569391e-02 1.05973557e-02 2.16634180e-02 ... 2.80352887e-02 1.55521873e-02 2.82677952e-02] [-2.29303762e-02 4.66355234e-02 7.91163836e-03 ... -6.14174758e-04 -7.07804322e-01 2.85902526e-02] [-1.77853629e-02 -3.00758495e-03 -2.55225878e-02 ... -2.40783971e-02 2.11018627e-03 2.69009806e-02] ... [ 6.05797209e-02 1.32483775e-02 2.69536003e-02 ... -1.38843581e-02 3.05043962e-02 3.85345481e-02] [ 6.33309558e-02 -3.04112374e-03 9.77444276e-03 ... 7.48321265e-02 3.42793856e-03 3.67484428e-02] [ 5.86028099e-02 5.84433973e-03 2.64811981e-03 ... 2.82612257e-02 -3.80136147e-02 3.29943895e-02]], shape=(1200, 1200), dtype=float32) Eigenvectors of original kernel matrix: tf.Tensor( [[ 0.03835681 0.0283473 -0.01169789 ... 0.02343717 0.0211248 0.03206972] [-0.04018159 0.00888097 -0.01388255 ... 0.00582427 0.717551 0.02881948] [-0.0166719 0.01350376 -0.03663862 ... 0.02467175 -0.00415936 0.02195409] ... [-0.03015648 -0.01671632 -0.01603392 ... 0.00100583 -0.00261221 0.02365689] [ 0.0039777 -0.04998879 -0.00528336 ... 0.01560401 -0.04330755 0.02782002] [-0.01665728 -0.00818616 -0.0432341 ... 0.00088256 0.00927396 0.01875088]], shape=(1200, 1200), dtype=float32)
¡Ahora tiene todo lo que necesita para volver a etiquetar el conjunto de datos! Ahora puede consultar el diagrama de flujo para comprender mejor cómo maximizar la separación del rendimiento al volver a etiquetar el conjunto de datos:
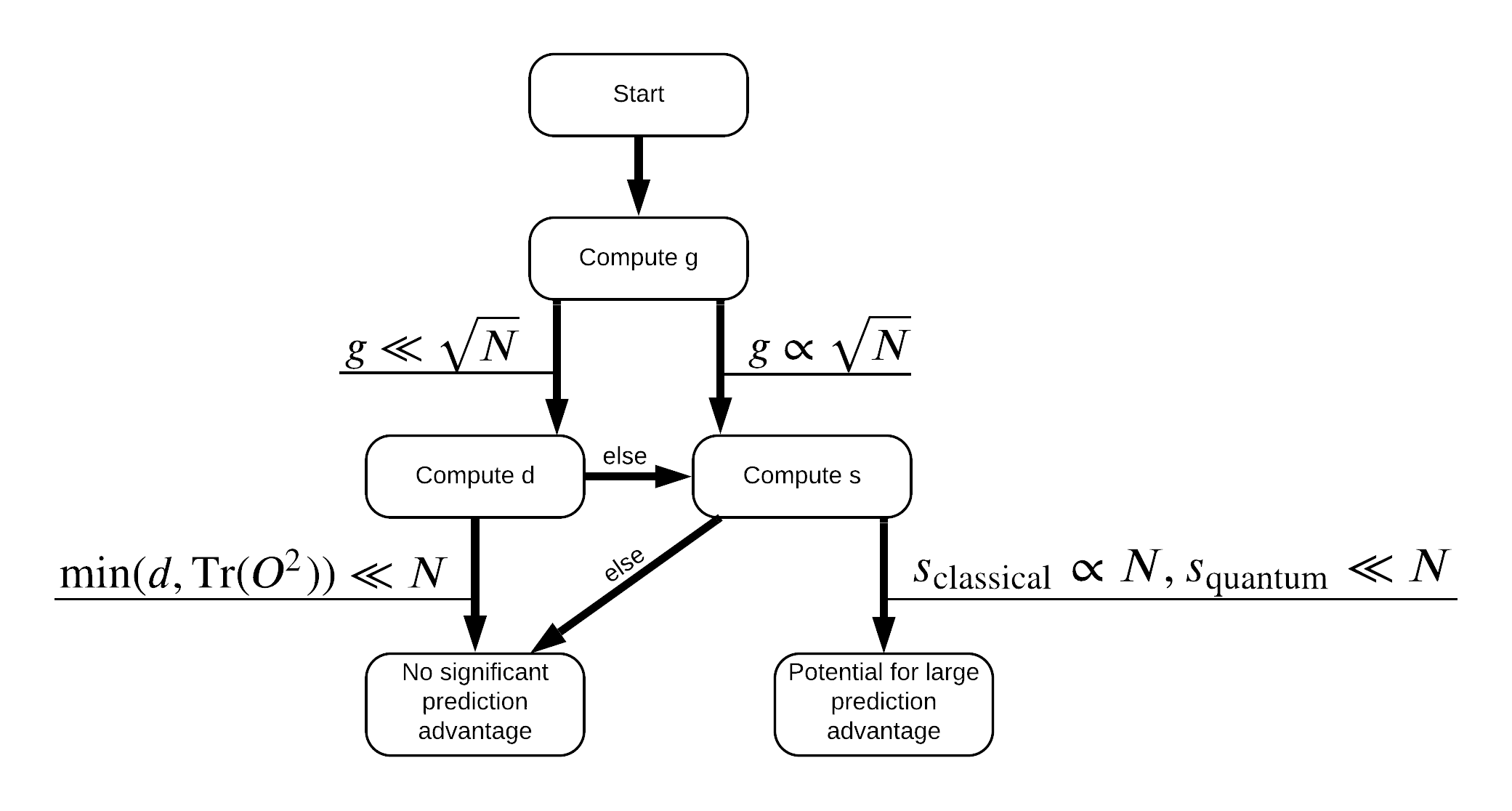
Con el fin de maximizar la separación entre cuántica y los modelos clásicos, se tratará de maximizar la diferencia geométrica entre el conjunto de datos original y el PQK características del núcleo matrices \(g(K_1 || K_2) = \sqrt{ || \sqrt{K_2} K_1^{-1} \sqrt{K_2} || _\infty}\) usando S_pqk, V_pqk y S_original, V_original . Un valor grande de \(g\) asegura que se mueve inicialmente hacia la derecha en el diagrama de flujo hacia abajo una ventaja de predicción en el caso cuántico.
def get_stilted_dataset(S, V, S_2, V_2, lambdav=1.1):
"""Prepare new labels that maximize geometric distance between kernels."""
S_diag = tf.linalg.diag(S ** 0.5)
S_2_diag = tf.linalg.diag(S_2 / (S_2 + lambdav) ** 2)
scaling = S_diag @ tf.transpose(V) @ \
V_2 @ S_2_diag @ tf.transpose(V_2) @ \
V @ S_diag
# Generate new lables using the largest eigenvector.
_, vecs = tf.linalg.eig(scaling)
new_labels = tf.math.real(
tf.einsum('ij,j->i', tf.cast(V @ S_diag, tf.complex64), vecs[-1])).numpy()
# Create new labels and add some small amount of noise.
final_y = new_labels > np.median(new_labels)
noisy_y = (final_y ^ (np.random.uniform(size=final_y.shape) > 0.95))
return noisy_y
y_relabel = get_stilted_dataset(S_pqk, V_pqk, S_original, V_original)
y_train_new, y_test_new = y_relabel[:N_TRAIN], y_relabel[N_TRAIN:]
3. Comparación de modelos
Ahora que ha preparado su conjunto de datos, es hora de comparar el rendimiento del modelo. Va a crear dos redes neuronales feedforward pequeña y comparar el rendimiento cuando se les da acceso a la PQK características que se encuentran en x_train_pqk .
3.1 Crear modelo mejorado de PQK
El uso estándar tf.keras operaciones de biblioteca Ahora puede crear un tren y un modelo en el x_train_pqk y y_train_new puntos de datos:
#docs_infra: no_execute
def create_pqk_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[len(qubits) * 3,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
pqk_model = create_pqk_model()
pqk_model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.003),
metrics=['accuracy'])
pqk_model.summary()
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense (Dense) (None, 32) 1088 _________________________________________________________________ dense_1 (Dense) (None, 16) 528 _________________________________________________________________ dense_2 (Dense) (None, 1) 17 ================================================================= Total params: 1,633 Trainable params: 1,633 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
pqk_history = pqk_model.fit(tf.reshape(x_train_pqk, [N_TRAIN, -1]),
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(tf.reshape(x_test_pqk, [N_TEST, -1]), y_test_new))
3.2 Crea un modelo clásico
De manera similar al código anterior, ahora también puede crear un modelo clásico que no tiene acceso a las funciones de PQK en su conjunto de datos sobre pilotes. Este modelo puede ser entrenado usando x_train y y_label_new .
#docs_infra: no_execute
def create_fair_classical_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[DATASET_DIM,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
model = create_fair_classical_model()
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.03),
metrics=['accuracy'])
model.summary()
Model: "sequential_1" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_3 (Dense) (None, 32) 352 _________________________________________________________________ dense_4 (Dense) (None, 16) 528 _________________________________________________________________ dense_5 (Dense) (None, 1) 17 ================================================================= Total params: 897 Trainable params: 897 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
classical_history = model.fit(x_train,
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(x_test, y_test_new))
3.3 Comparar el rendimiento
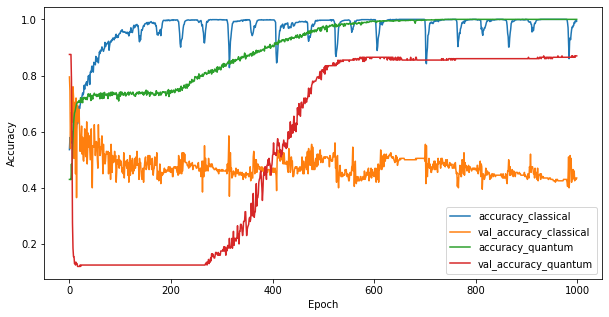
Ahora que ha entrenado los dos modelos, puede trazar rápidamente las brechas de rendimiento en los datos de validación entre los dos. Normalmente, ambos modelos lograrán una precisión> 0,9 en los datos de entrenamiento. Sin embargo, en los datos de validación, queda claro que solo la información que se encuentra en las características de PQK es suficiente para que el modelo se generalice bien a instancias invisibles.
#docs_infra: no_execute
plt.figure(figsize=(10,5))
plt.plot(classical_history.history['accuracy'], label='accuracy_classical')
plt.plot(classical_history.history['val_accuracy'], label='val_accuracy_classical')
plt.plot(pqk_history.history['accuracy'], label='accuracy_quantum')
plt.plot(pqk_history.history['val_accuracy'], label='val_accuracy_quantum')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
<matplotlib.legend.Legend at 0x7f6d846ecee0>
4. Conclusiones importantes
Hay varias conclusiones importantes que se pueden extraer de esto y los MNIST experimentos:
Es muy poco probable que los modelos cuánticos de hoy superen el rendimiento del modelo clásico en datos clásicos. Especialmente en los conjuntos de datos clásicos de hoy que pueden tener más de un millón de puntos de datos.
El hecho de que los datos puedan provenir de un circuito cuántico difícil de simular clásicamente, no necesariamente hace que los datos sean difíciles de aprender para un modelo clásico.
Existen conjuntos de datos (en última instancia de naturaleza cuántica) que son fáciles de aprender para los modelos cuánticos y difíciles de aprender para los modelos clásicos, independientemente de la arquitectura del modelo o los algoritmos de entrenamiento utilizados.
