 TensorFlow.org で実行 |
 Google Colabで実行 |
 GitHub で表示 |
 ノートブックをダウンロード |
 TF Hub モデルを参照 |
TF-Hub (https://tfhub.dev/tensorflow/cord-19/swivel-128d/3) の CORD-19 Swivel テキスト埋め込みモジュールは、COVID-19 に関連する自然言語テキストを分析する研究者をサポートするために構築されました。これらの埋め込みは、CORD-19 データセットの論文のタイトル、著者、抄録、本文、および参照タイトルをトレーニングしています。
この Colab では、以下について取り上げます。
- 埋め込み空間内の意味的に類似した単語の分析
- CORD-19 埋め込みを使用した SciCite データセットによる分類器のトレーニング
セットアップ
import functools
import itertools
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_hub as hub
from tqdm import trange
2022-08-08 18:54:14.303070: E tensorflow/stream_executor/cuda/cuda_blas.cc:2981] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered 2022-08-08 18:54:14.990911: W tensorflow/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer.so.7'; dlerror: libnvrtc.so.11.1: cannot open shared object file: No such file or directory 2022-08-08 18:54:14.991239: W tensorflow/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer_plugin.so.7'; dlerror: libnvrtc.so.11.1: cannot open shared object file: No such file or directory 2022-08-08 18:54:14.991254: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Cannot dlopen some TensorRT libraries. If you would like to use Nvidia GPU with TensorRT, please make sure the missing libraries mentioned above are installed properly.
埋め込みを分析する
まず、異なる単語間の相関行列を計算してプロットし、埋め込みを分析してみましょう。異なる単語の意味をうまく捉えられるように埋め込みが学習できていれば、意味的に似た単語の埋め込みベクトルは近くにあるはずです。COVID-19 関連の用語をいくつか見てみましょう。
# Use the inner product between two embedding vectors as the similarity measure
def plot_correlation(labels, features):
corr = np.inner(features, features)
corr /= np.max(corr)
sns.heatmap(corr, xticklabels=labels, yticklabels=labels)
# Generate embeddings for some terms
queries = [
# Related viruses
'coronavirus', 'SARS', 'MERS',
# Regions
'Italy', 'Spain', 'Europe',
# Symptoms
'cough', 'fever', 'throat'
]
module = hub.load('https://tfhub.dev/tensorflow/cord-19/swivel-128d/3')
embeddings = module(queries)
plot_correlation(queries, embeddings)
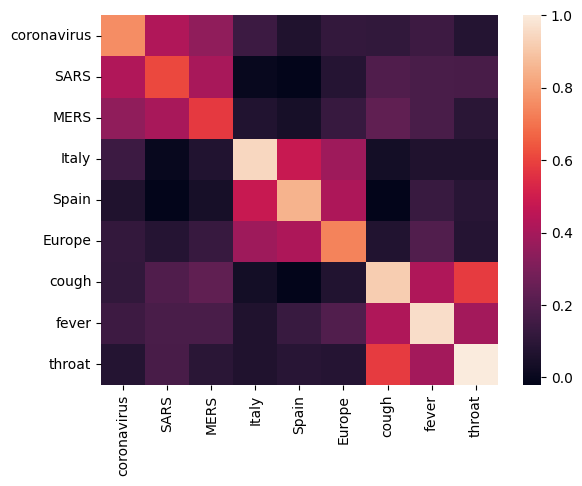
埋め込みが異なる用語の意味をうまく捉えていることが分かります。それぞれの単語は所属するクラスタの他の単語に類似していますが（「コロナウイルス」は「SARS」や「MERS」と高い関連性がある）、ほかのクラスタの単語とは異なります（「SARS」と「スペイン」の類似度はゼロに近い）。
では、これらの埋め込みを使用して特定のタスクを解決する方法を見てみましょう。
SciCite: 引用の意図の分類
このセクションでは、テキスト分類など下流のタスクに埋め込みを使う方法を示します。学術論文の引用の意図の分類には、TensorFlow Dataset の SciCite データセットを使用します。学術論文からの引用がある文章がある場合に、その引用の主な意図が背景情報、方法の使用、または結果の比較のうち、どれであるかを分類します。
builder = tfds.builder(name='scicite')
builder.download_and_prepare()
train_data, validation_data, test_data = builder.as_dataset(
split=('train', 'validation', 'test'),
as_supervised=True)
Let's take a look at a few labeled examples from the training set
NUM_EXAMPLES = 10
TEXT_FEATURE_NAME = builder.info.supervised_keys[0]
LABEL_NAME = builder.info.supervised_keys[1]
def label2str(numeric_label):
m = builder.info.features[LABEL_NAME].names
return m[numeric_label]
data = next(iter(train_data.batch(NUM_EXAMPLES)))
pd.DataFrame({
TEXT_FEATURE_NAME: [ex.numpy().decode('utf8') for ex in data[0]],
LABEL_NAME: [label2str(x) for x in data[1]]
})
引用の意図分類器をトレーニングする
分類器のトレーニングには、SciCite データセットに対して Keras を使用します。上に分類レイヤーを持ち、CORD-19 埋め込みを使用するモデルを構築してみましょう。
Hyperparameters
EMBEDDING = 'https://tfhub.dev/tensorflow/cord-19/swivel-128d/3'
TRAINABLE_MODULE = False
hub_layer = hub.KerasLayer(EMBEDDING, input_shape=[],
dtype=tf.string, trainable=TRAINABLE_MODULE)
model = tf.keras.Sequential()
model.add(hub_layer)
model.add(tf.keras.layers.Dense(3))
model.summary()
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
WARNING:tensorflow:Please fix your imports. Module tensorflow.python.training.tracking.data_structures has been moved to tensorflow.python.trackable.data_structures. The old module will be deleted in version 2.11.
WARNING:tensorflow:Please fix your imports. Module tensorflow.python.training.tracking.data_structures has been moved to tensorflow.python.trackable.data_structures. The old module will be deleted in version 2.11.
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
keras_layer (KerasLayer) (None, 128) 17301632
dense (Dense) (None, 3) 387
=================================================================
Total params: 17,302,019
Trainable params: 387
Non-trainable params: 17,301,632
_________________________________________________________________
モデルをトレーニングして評価する
モデルをトレーニングして評価を行い、SciCite タスクでのパフォーマンスを見てみましょう。
EPOCHS = 35
BATCH_SIZE = 32
history = model.fit(train_data.shuffle(10000).batch(BATCH_SIZE),
epochs=EPOCHS,
validation_data=validation_data.batch(BATCH_SIZE),
verbose=1)
Epoch 1/35 257/257 [==============================] - 2s 5ms/step - loss: 0.8885 - accuracy: 0.5997 - val_loss: 0.7476 - val_accuracy: 0.6998 Epoch 2/35 257/257 [==============================] - 1s 4ms/step - loss: 0.6824 - accuracy: 0.7255 - val_loss: 0.6596 - val_accuracy: 0.7489 Epoch 3/35 257/257 [==============================] - 1s 4ms/step - loss: 0.6190 - accuracy: 0.7556 - val_loss: 0.6184 - val_accuracy: 0.7533 Epoch 4/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5867 - accuracy: 0.7696 - val_loss: 0.5964 - val_accuracy: 0.7609 Epoch 5/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5682 - accuracy: 0.7787 - val_loss: 0.5846 - val_accuracy: 0.7686 Epoch 6/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5553 - accuracy: 0.7855 - val_loss: 0.5751 - val_accuracy: 0.7686 Epoch 7/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5462 - accuracy: 0.7883 - val_loss: 0.5720 - val_accuracy: 0.7697 Epoch 8/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5397 - accuracy: 0.7886 - val_loss: 0.5661 - val_accuracy: 0.7751 Epoch 9/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5350 - accuracy: 0.7896 - val_loss: 0.5610 - val_accuracy: 0.7729 Epoch 10/35 257/257 [==============================] - 1s 5ms/step - loss: 0.5302 - accuracy: 0.7931 - val_loss: 0.5597 - val_accuracy: 0.7773 Epoch 11/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5271 - accuracy: 0.7928 - val_loss: 0.5560 - val_accuracy: 0.7762 Epoch 12/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5235 - accuracy: 0.7946 - val_loss: 0.5543 - val_accuracy: 0.7784 Epoch 13/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5207 - accuracy: 0.7947 - val_loss: 0.5592 - val_accuracy: 0.7795 Epoch 14/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5193 - accuracy: 0.7925 - val_loss: 0.5508 - val_accuracy: 0.7773 Epoch 15/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5166 - accuracy: 0.7951 - val_loss: 0.5507 - val_accuracy: 0.7806 Epoch 16/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5147 - accuracy: 0.7953 - val_loss: 0.5518 - val_accuracy: 0.7784 Epoch 17/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5131 - accuracy: 0.7969 - val_loss: 0.5486 - val_accuracy: 0.7762 Epoch 18/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5118 - accuracy: 0.7964 - val_loss: 0.5519 - val_accuracy: 0.7806 Epoch 19/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5105 - accuracy: 0.7972 - val_loss: 0.5473 - val_accuracy: 0.7806 Epoch 20/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5093 - accuracy: 0.7994 - val_loss: 0.5469 - val_accuracy: 0.7828 Epoch 21/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5082 - accuracy: 0.7985 - val_loss: 0.5482 - val_accuracy: 0.7806 Epoch 22/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5071 - accuracy: 0.7986 - val_loss: 0.5493 - val_accuracy: 0.7849 Epoch 23/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5066 - accuracy: 0.7984 - val_loss: 0.5475 - val_accuracy: 0.7849 Epoch 24/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5056 - accuracy: 0.7970 - val_loss: 0.5439 - val_accuracy: 0.7828 Epoch 25/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5052 - accuracy: 0.7988 - val_loss: 0.5452 - val_accuracy: 0.7838 Epoch 26/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5041 - accuracy: 0.8005 - val_loss: 0.5463 - val_accuracy: 0.7806 Epoch 27/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5035 - accuracy: 0.8000 - val_loss: 0.5473 - val_accuracy: 0.7806 Epoch 28/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5024 - accuracy: 0.8021 - val_loss: 0.5444 - val_accuracy: 0.7817 Epoch 29/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5019 - accuracy: 0.7999 - val_loss: 0.5441 - val_accuracy: 0.7838 Epoch 30/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5012 - accuracy: 0.8002 - val_loss: 0.5484 - val_accuracy: 0.7817 Epoch 31/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5014 - accuracy: 0.8007 - val_loss: 0.5435 - val_accuracy: 0.7860 Epoch 32/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5004 - accuracy: 0.8011 - val_loss: 0.5456 - val_accuracy: 0.7849 Epoch 33/35 257/257 [==============================] - 1s 4ms/step - loss: 0.5007 - accuracy: 0.7991 - val_loss: 0.5465 - val_accuracy: 0.7871 Epoch 34/35 257/257 [==============================] - 1s 4ms/step - loss: 0.4987 - accuracy: 0.7994 - val_loss: 0.5463 - val_accuracy: 0.7838 Epoch 35/35 257/257 [==============================] - 1s 4ms/step - loss: 0.4990 - accuracy: 0.8013 - val_loss: 0.5491 - val_accuracy: 0.7806
from matplotlib import pyplot as plt
def display_training_curves(training, validation, title, subplot):
if subplot%10==1: # set up the subplots on the first call
plt.subplots(figsize=(10,10), facecolor='#F0F0F0')
plt.tight_layout()
ax = plt.subplot(subplot)
ax.set_facecolor('#F8F8F8')
ax.plot(training)
ax.plot(validation)
ax.set_title('model '+ title)
ax.set_ylabel(title)
ax.set_xlabel('epoch')
ax.legend(['train', 'valid.'])
display_training_curves(history.history['accuracy'], history.history['val_accuracy'], 'accuracy', 211)
display_training_curves(history.history['loss'], history.history['val_loss'], 'loss', 212)
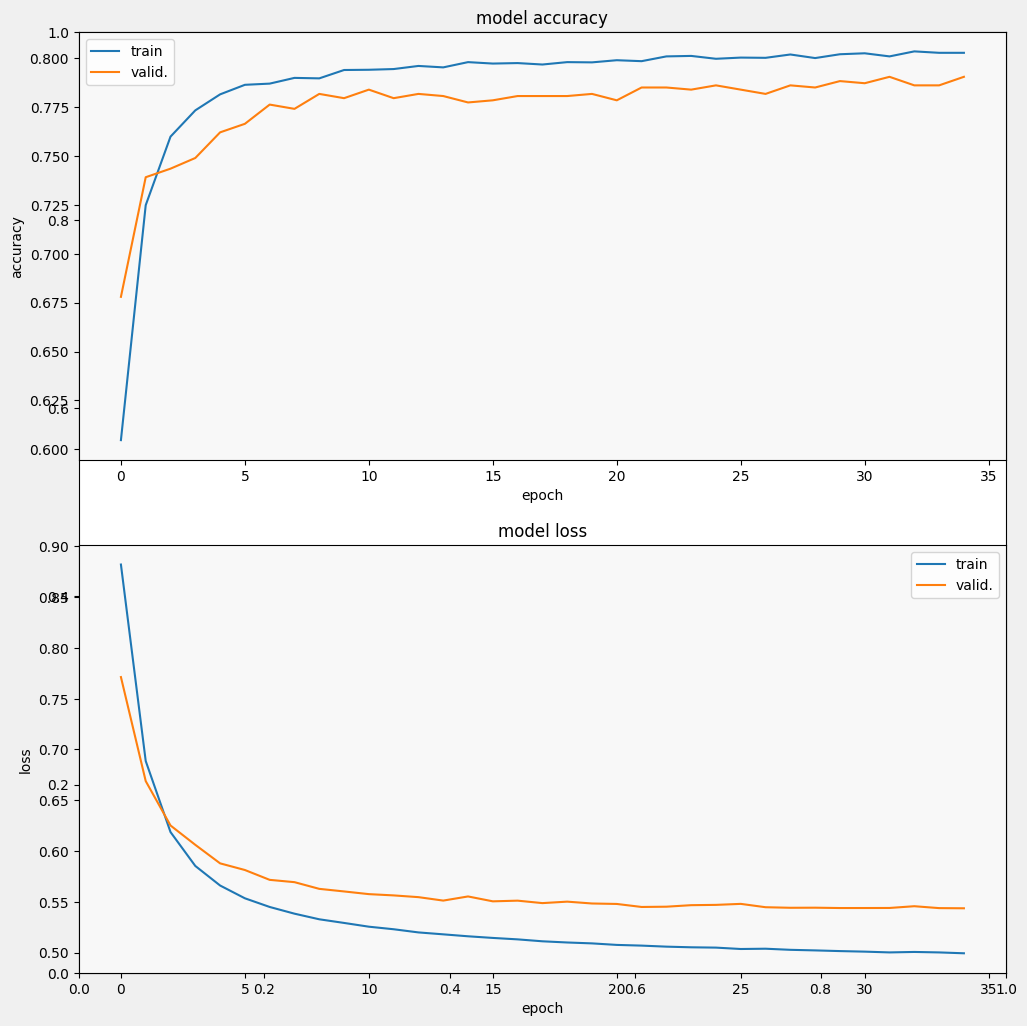
モデルを評価する
モデルがどのように実行するか見てみましょう。2 つの値が返されます。損失（誤差、値が低いほど良）と精度です。
results = model.evaluate(test_data.batch(512), verbose=2)
for name, value in zip(model.metrics_names, results):
print('%s: %.3f' % (name, value))
4/4 - 0s - loss: 0.5350 - accuracy: 0.7913 - 292ms/epoch - 73ms/step loss: 0.535 accuracy: 0.791
損失はすぐに減少しますが、特に精度は急速に上がることが分かります。予測と真のラベルがどのように関係しているかを確認するために、いくつかの例をプロットしてみましょう。
prediction_dataset = next(iter(test_data.batch(20)))
prediction_texts = [ex.numpy().decode('utf8') for ex in prediction_dataset[0]]
prediction_labels = [label2str(x) for x in prediction_dataset[1]]
predictions = [
label2str(x) for x in np.argmax(model.predict(prediction_texts), axis=-1)]
pd.DataFrame({
TEXT_FEATURE_NAME: prediction_texts,
LABEL_NAME: prediction_labels,
'prediction': predictions
})
1/1 [==============================] - 0s 154ms/step
このランダムサンプルでは、ほとんどの場合、モデルが正しいラベルを予測しており、科学的な文章をうまく埋め込むことができていることが分かります。
次のステップ
TF-Hub の CORD-19 Swivel 埋め込みについて少し説明しました。COVID-19 関連の学術的なテキストから科学的洞察の取得に貢献できる、CORD-19 Kaggle コンペへの参加をお勧めします。
- CORD-19 Kaggle Challenge に参加しましょう。
- 詳細については COVID-19 Open Research Dataset (CORD-19) をご覧ください。
- TF-Hub 埋め込みに関する詳細のドキュメントは https://tfhub.dev/tensorflow/cord-19/swivel-128d/1 をご覧ください。
- TensorFlow Embedding Projector を利用して CORD-19 埋め込み空間を見てみましょう。