 View on TensorFlow.org View on TensorFlow.org
|
 Run in Google Colab Run in Google Colab
|
 View on GitHub View on GitHub
|
 Download notebook Download notebook
|
 See TF Hub model See TF Hub model
|
This Colab demonstrates use of a TF Hub module based on a generative adversarial network (GAN). The module maps from N-dimensional vectors, called latent space, to RGB images.
Two examples are provided:
- Mapping from latent space to images, and
- Given a target image, using gradient descent to find a latent vector that generates an image similar to the target image.
Optional prerequisites
- Familiarity with low level Tensorflow concepts.
- Generative Adversarial Network on Wikipedia.
- Paper on Progressive GANs: Progressive Growing of GANs for Improved Quality, Stability, and Variation.
More models
Here you can find all models currently hosted on tfhub.dev that can generate images.
Setup
# Install imageio for creating animations.pip -q install imageiopip -q install scikit-imagepip install git+https://github.com/tensorflow/docs
Imports and function definitions
from absl import logging
import imageio
import PIL.Image
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
tf.random.set_seed(0)
import tensorflow_hub as hub
from tensorflow_docs.vis import embed
import time
try:
from google.colab import files
except ImportError:
pass
from IPython import display
from skimage import transform
# We could retrieve this value from module.get_input_shapes() if we didn't know
# beforehand which module we will be using.
latent_dim = 512
# Interpolates between two vectors that are non-zero and don't both lie on a
# line going through origin. First normalizes v2 to have the same norm as v1.
# Then interpolates between the two vectors on the hypersphere.
def interpolate_hypersphere(v1, v2, num_steps):
v1_norm = tf.norm(v1)
v2_norm = tf.norm(v2)
v2_normalized = v2 * (v1_norm / v2_norm)
vectors = []
for step in range(num_steps):
interpolated = v1 + (v2_normalized - v1) * step / (num_steps - 1)
interpolated_norm = tf.norm(interpolated)
interpolated_normalized = interpolated * (v1_norm / interpolated_norm)
vectors.append(interpolated_normalized)
return tf.stack(vectors)
# Simple way to display an image.
def display_image(image):
image = tf.constant(image)
image = tf.image.convert_image_dtype(image, tf.uint8)
return PIL.Image.fromarray(image.numpy())
# Given a set of images, show an animation.
def animate(images):
images = np.array(images)
converted_images = np.clip(images * 255, 0, 255).astype(np.uint8)
imageio.mimsave('./animation.gif', converted_images)
return embed.embed_file('./animation.gif')
logging.set_verbosity(logging.ERROR)
Latent space interpolation
Random vectors
Latent space interpolation between two randomly initialized vectors. We will use a TF Hub module progan-128 that contains a pre-trained Progressive GAN.
progan = hub.load("https://tfhub.dev/google/progan-128/1").signatures['default']
2024-03-09 13:17:20.450855: E external/local_xla/xla/stream_executor/cuda/cuda_driver.cc:282] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
def interpolate_between_vectors():
v1 = tf.random.normal([latent_dim])
v2 = tf.random.normal([latent_dim])
# Creates a tensor with 25 steps of interpolation between v1 and v2.
vectors = interpolate_hypersphere(v1, v2, 50)
# Uses module to generate images from the latent space.
interpolated_images = progan(vectors)['default']
return interpolated_images
interpolated_images = interpolate_between_vectors()
animate(interpolated_images)

Finding closest vector in latent space
Fix a target image. As an example use an image generated from the module or upload your own.
image_from_module_space = True # @param { isTemplate:true, type:"boolean" }
def get_module_space_image():
vector = tf.random.normal([1, latent_dim])
images = progan(vector)['default'][0]
return images
def upload_image():
uploaded = files.upload()
image = imageio.imread(uploaded[list(uploaded.keys())[0]])
return transform.resize(image, [128, 128])
if image_from_module_space:
target_image = get_module_space_image()
else:
target_image = upload_image()
display_image(target_image)

After defining a loss function between the target image and the image generated by a latent space variable, we can use gradient descent to find variable values that minimize the loss.
tf.random.set_seed(42)
initial_vector = tf.random.normal([1, latent_dim])
display_image(progan(initial_vector)['default'][0])

def find_closest_latent_vector(initial_vector, num_optimization_steps,
steps_per_image):
images = []
losses = []
vector = tf.Variable(initial_vector)
optimizer = tf.optimizers.Adam(learning_rate=0.01)
loss_fn = tf.losses.MeanAbsoluteError(reduction="sum")
for step in range(num_optimization_steps):
if (step % 100)==0:
print()
print('.', end='')
with tf.GradientTape() as tape:
image = progan(vector.read_value())['default'][0]
if (step % steps_per_image) == 0:
images.append(image.numpy())
target_image_difference = loss_fn(image, target_image[:,:,:3])
# The latent vectors were sampled from a normal distribution. We can get
# more realistic images if we regularize the length of the latent vector to
# the average length of vector from this distribution.
regularizer = tf.abs(tf.norm(vector) - np.sqrt(latent_dim))
loss = target_image_difference + regularizer
losses.append(loss.numpy())
grads = tape.gradient(loss, [vector])
optimizer.apply_gradients(zip(grads, [vector]))
return images, losses
num_optimization_steps=200
steps_per_image=5
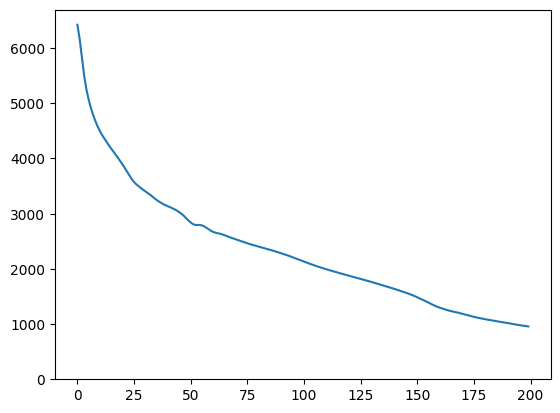
images, loss = find_closest_latent_vector(initial_vector, num_optimization_steps, steps_per_image)
.................................................................................................... ....................................................................................................
plt.plot(loss)
plt.ylim([0,max(plt.ylim())])
(0.0, 6696.3041717529295)
animate(np.stack(images))

Compare the result to the target:
display_image(np.concatenate([images[-1], target_image], axis=1))

Playing with the above example
If image is from the module space, the descent is quick and converges to a reasonable sample. Try out descending to an image that is not from the module space. The descent will only converge if the image is reasonably close to the space of training images.
How to make it descend faster and to a more realistic image? One can try:
- using different loss on the image difference, e.g., quadratic,
- using different regularizer on the latent vector,
- initializing from a random vector in multiple runs,
- etc.
