TensorFlow Lattice est une bibliothèque qui implémente des modèles basés sur un réseau flexibles, contrôlés et interprétables. La bibliothèque vous permet d'injecter des connaissances du domaine dans le processus d'apprentissage grâce à des contraintes de forme fondées sur le bon sens ou fondées sur des politiques. Cela se fait en utilisant une collection de couches Keras qui peuvent satisfaire des contraintes telles que la monotonie, la convexité et la confiance par paires. La bibliothèque fournit également des modèles prédéfinis faciles à configurer.
Concepts
Cette section est une version simplifiée de la description dans Tableaux de recherche interpolés calibrés monotoniques , JMLR 2016.
Treillis
Un treillis est une table de recherche interpolée qui peut approximer des relations entrée-sortie arbitraires dans vos données. Il superpose une grille régulière sur votre espace d'entrée et apprend les valeurs de sortie dans les sommets de la grille. Pour un point de test \(x\), \(f(x)\) est interpolé linéairement à partir des valeurs de réseau entourant \(x\).
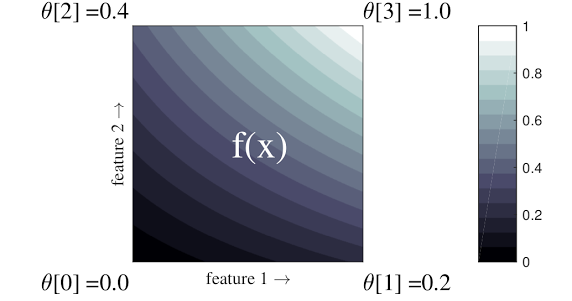
L'exemple simple ci-dessus est une fonction avec 2 fonctionnalités d'entrée et 4 paramètres :\(\theta=[0, 0.2, 0.4, 1]\), qui sont les valeurs de la fonction aux coins de l'espace d'entrée ; le reste de la fonction est interpolé à partir de ces paramètres.
La fonction \(f(x)\) peut capturer des interactions non linéaires entre les fonctionnalités. Vous pouvez considérer les paramètres du réseau comme la hauteur des poteaux fixés dans le sol sur une grille régulière, et la fonction résultante est comme un tissu serré contre les quatre poteaux.
Avec \(D\) entités et 2 sommets le long de chaque dimension, un treillis régulier aura \(2^D\) paramètres. Pour adapter une fonction plus flexible, vous pouvez spécifier un réseau à granularité plus fine sur l'espace des fonctionnalités avec plus de sommets le long de chaque dimension. Les fonctions de régression sur réseau sont continues et infiniment différentiables par morceaux.
Étalonnage
Supposons que l'exemple de réseau précédent représente le bonheur d'un utilisateur averti avec une suggestion de café local calculée à l'aide de fonctionnalités :
- prix du café, compris entre 0 et 20 dollars
- distance à l'utilisateur, dans une plage de 0 à 30 kilomètres
Nous voulons que notre modèle apprenne le bonheur des utilisateurs avec une suggestion de café local. Les modèles de treillis TensorFlow peuvent utiliser des fonctions linéaires par morceaux (avec tfl.layers.PWLCalibration ) pour calibrer et normaliser les caractéristiques d'entrée selon la plage acceptée par le réseau : 0,0 à 1,0 dans l'exemple de réseau ci-dessus. Les exemples suivants montrent des exemples de telles fonctions d'étalonnage avec 10 points clés :
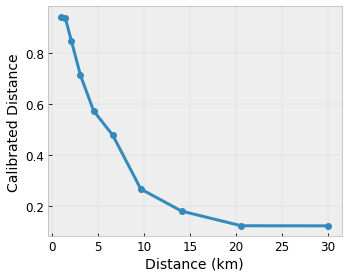
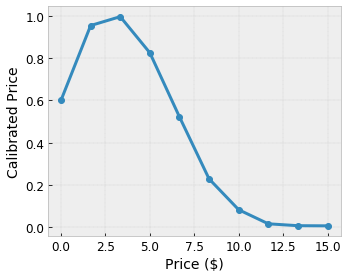
C'est souvent une bonne idée d'utiliser les quantiles des caractéristiques comme points clés d'entrée. Les modèles prédéfinis TensorFlow Lattice peuvent définir automatiquement les points clés d'entrée sur les quantiles de caractéristiques.
Pour les fonctionnalités catégorielles, TensorFlow Lattice fournit un étalonnage catégoriel (avec tfl.layers.CategoricalCalibration ) avec une limite de sortie similaire à alimenter dans un réseau.
Ensembles
Le nombre de paramètres d'une couche de réseau augmente de façon exponentielle avec le nombre d'entités en entrée, ce qui ne s'adapte donc pas bien aux dimensions très élevées. Pour surmonter cette limitation, TensorFlow Lattice propose des ensembles de réseaux qui combinent (en moyenne) plusieurs petits réseaux, ce qui permet au modèle de croître linéairement en nombre de fonctionnalités.
La bibliothèque propose deux variantes de ces ensembles :
Random Tiny Lattices (RTL) : chaque sous-modèle utilise un sous-ensemble aléatoire de fonctionnalités (avec remplacement).
Crystals : l'algorithme Crystals entraîne d'abord un modèle de préajustement qui estime les interactions de fonctionnalités par paires. Il organise ensuite l'ensemble final de telle sorte que les entités présentant davantage d'interactions non linéaires se trouvent dans les mêmes réseaux.
Pourquoi le treillis TensorFlow ?
Vous pouvez trouver une brève introduction à TensorFlow Lattice dans cet article du blog TF .
Interprétabilité
Étant donné que les paramètres de chaque couche sont la sortie de cette couche, il est facile d'analyser, de comprendre et de déboguer chaque partie du modèle.
Modèles précis et flexibles
En utilisant des réseaux à grain fin, vous pouvez obtenir des fonctions arbitrairement complexes avec une seule couche de réseau. L'utilisation de plusieurs couches de calibrateurs et de réseaux fonctionne souvent bien dans la pratique et peut correspondre ou surpasser les modèles DNN de tailles similaires.
Contraintes de forme de bon sens
Les données d'entraînement réelles peuvent ne pas représenter suffisamment les données d'exécution. Les solutions de ML flexibles telles que les DNN ou les forêts agissent souvent de manière inattendue, voire sauvage, dans des parties de l'espace d'entrée non couvertes par les données d'entraînement. Ce comportement est particulièrement problématique lorsque les contraintes politiques ou d’équité peuvent être violées.
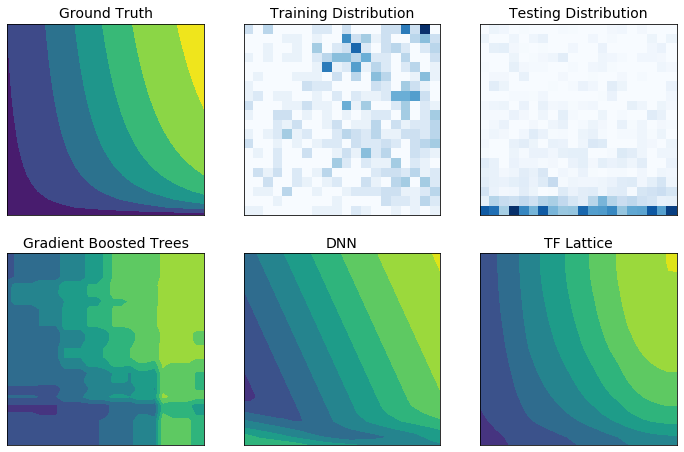
Même si les formes courantes de régularisation peuvent aboutir à une extrapolation plus judicieuse, les régularisateurs standards ne peuvent pas garantir un comportement raisonnable du modèle dans l'ensemble de l'espace d'entrée, en particulier avec des entrées de grande dimension. Le passage à des modèles plus simples avec un comportement plus contrôlé et prévisible peut avoir un coût important en termes de précision du modèle.
TF Lattice permet de continuer à utiliser des modèles flexibles, mais offre plusieurs options pour injecter des connaissances du domaine dans le processus d'apprentissage à travers des contraintes de forme sémantiquement significatives ou motivées par des politiques :
- Monotonie : Vous pouvez spécifier que la sortie ne doit augmenter/diminuer que par rapport à une entrée. Dans notre exemple, vous souhaiterez peut-être spécifier que l'augmentation de la distance jusqu'à un café ne devrait que diminuer la préférence prévue de l'utilisateur.
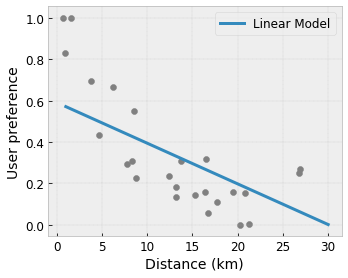
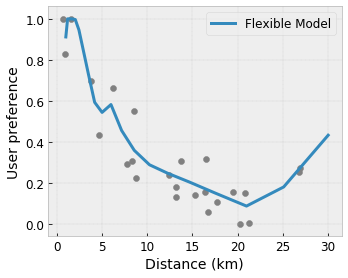
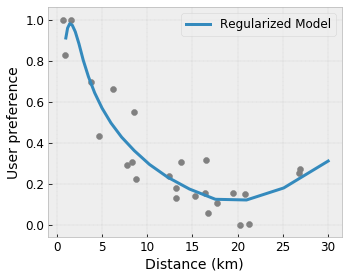
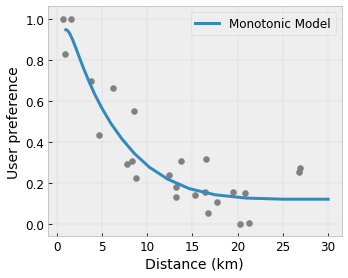
Convexité/Concavité : Vous pouvez spécifier que la forme de la fonction peut être convexe ou concave. Mélangé à la monotonie, cela peut forcer la fonction à représenter des rendements décroissants par rapport à une caractéristique donnée.
Unimodalité : Vous pouvez spécifier que la fonction doit avoir un pic ou une vallée unique. Cela vous permet de représenter des fonctions qui ont un point idéal par rapport à une fonctionnalité.
Confiance par paire : cette contrainte fonctionne sur une paire de fonctionnalités et suggère qu'une fonctionnalité d'entrée reflète sémantiquement la confiance dans une autre fonctionnalité. Par exemple, un nombre plus élevé d’avis vous rend plus confiant dans la note moyenne d’un restaurant. Le modèle sera plus sensible par rapport à la note (c'est-à-dire aura une pente plus grande par rapport à la note) lorsque le nombre d'avis est plus élevé.
Flexibilité contrôlée avec les régularisateurs
En plus des contraintes de forme, le treillis TensorFlow fournit un certain nombre de régularisateurs pour contrôler la flexibilité et la fluidité de la fonction pour chaque couche.
Régulateur laplacien : les sorties du réseau/sommets de calibrage/points clés sont régularisées vers les valeurs de leurs voisins respectifs. Il en résulte une fonction plus plate .
Hessian Regularizer : Cela pénalise la dérivée première de la couche d'étalonnage PWL pour rendre la fonction plus linéaire .
Wrinkle Regularizer : Ceci pénalise la dérivée seconde de la couche de calibrage PWL pour éviter des changements brusques de courbure. Cela rend la fonction plus fluide.
Régulateur de torsion : les sorties du réseau seront régularisées pour empêcher la torsion entre les entités. En d’autres termes, le modèle sera régularisé vers l’indépendance entre les contributions des fonctionnalités.
Mélangez et assortissez avec d'autres couches Keras
Vous pouvez utiliser les couches TF Lattice en combinaison avec d'autres couches Keras pour construire des modèles partiellement contraints ou régularisés. Par exemple, des couches d'étalonnage de réseau ou PWL peuvent être utilisées au niveau de la dernière couche de réseaux plus profonds qui incluent des intégrations ou d'autres couches Keras.
Papiers
- Éthique déontologique par contraintes de forme monotonique , Serena Wang, Maya Gupta, Conférence internationale sur l'intelligence artificielle et les statistiques (AISSTATS), 2020
- Contraintes de forme pour les fonctions d'ensemble , Andrew Cotter, Maya Gupta, H. Jiang, Erez Louidor, Jim Muller, Taman Narayan, Serena Wang, Tao Zhu. Conférence internationale sur l'apprentissage automatique (ICML), 2019
- Les rendements décroissants façonnent les contraintes d'interprétabilité et de régularisation , Maya Gupta, Dara Bahri, Andrew Cotter, Kevin Canini, Advances in Neural Information Processing Systems (NeurIPS), 2018
- Réseaux à treillis profonds et fonctions monotoniques partielles , Seungil You, Kevin Canini, David Ding, Jan Pfeifer, Maya R. Gupta, Advances in Neural Information Processing Systems (NeurIPS), 2017
- Fonctions monotones rapides et flexibles avec des ensembles de réseaux , Mahdi Milani Fard, Kevin Canini, Andrew Cotter, Jan Pfeifer, Maya Gupta, Advances in Neural Information Processing Systems (NeurIPS), 2016
- Tables de recherche interpolées calibrées monotones , Maya Gupta, Andrew Cotter, Jan Pfeifer, Konstantin Voevodski, Kevin Canini, Alexander Mangylov, Wojciech Moczydlowski, Alexander van Esbroeck, Journal of Machine Learning Research (JMLR), 2016
- Régression optimisée pour une évaluation efficace des fonctions , Eric Garcia, Raman Arora, Maya R. Gupta, IEEE Transactions on Image Processing, 2012
- Régression sur réseau , Eric Garcia, Maya Gupta, Advances in Neural Information Processing Systems (NeurIPS), 2009
Tutoriels et documents API
Pour les architectures de modèles courantes, vous pouvez utiliser des modèles prédéfinis Keras . Vous pouvez également créer des modèles personnalisés à l’aide des calques TF Lattice Keras ou les mélanger avec d’autres calques Keras. Consultez la documentation complète de l'API pour plus de détails.
,TensorFlow Lattice est une bibliothèque qui implémente des modèles basés sur un réseau flexibles, contrôlés et interprétables. La bibliothèque vous permet d'injecter des connaissances du domaine dans le processus d'apprentissage grâce à des contraintes de forme fondées sur le bon sens ou fondées sur des politiques. Cela se fait à l'aide d'un ensemble de couches Keras qui peuvent satisfaire des contraintes telles que la monotonie, la convexité et la confiance par paires. La bibliothèque fournit également des modèles prédéfinis faciles à configurer.
Concepts
Cette section est une version simplifiée de la description dans Tableaux de recherche interpolés calibrés monotoniques , JMLR 2016.
Treillis
Un treillis est une table de recherche interpolée qui peut approximer des relations entrée-sortie arbitraires dans vos données. Il superpose une grille régulière sur votre espace d'entrée et apprend les valeurs de sortie dans les sommets de la grille. Pour un point de test \(x\), \(f(x)\) est interpolé linéairement à partir des valeurs de réseau entourant \(x\).

L'exemple simple ci-dessus est une fonction avec 2 fonctionnalités d'entrée et 4 paramètres :\(\theta=[0, 0.2, 0.4, 1]\), qui sont les valeurs de la fonction aux coins de l'espace d'entrée ; le reste de la fonction est interpolé à partir de ces paramètres.
La fonction \(f(x)\) peut capturer des interactions non linéaires entre les fonctionnalités. Vous pouvez considérer les paramètres du réseau comme la hauteur des poteaux fixés dans le sol sur une grille régulière, et la fonction résultante est comme un tissu serré contre les quatre poteaux.
Avec \(D\) entités et 2 sommets le long de chaque dimension, un treillis régulier aura \(2^D\) paramètres. Pour adapter une fonction plus flexible, vous pouvez spécifier un réseau à granularité plus fine sur l'espace des fonctionnalités avec plus de sommets le long de chaque dimension. Les fonctions de régression sur réseau sont continues et infiniment différentiables par morceaux.
Étalonnage
Supposons que l'exemple de réseau précédent représente le bonheur d'un utilisateur averti avec une suggestion de café local calculée à l'aide de fonctionnalités :
- prix du café, compris entre 0 et 20 dollars
- distance à l'utilisateur, dans une plage de 0 à 30 kilomètres
Nous voulons que notre modèle apprenne le bonheur des utilisateurs avec une suggestion de café local. Les modèles de treillis TensorFlow peuvent utiliser des fonctions linéaires par morceaux (avec tfl.layers.PWLCalibration ) pour calibrer et normaliser les caractéristiques d'entrée selon la plage acceptée par le réseau : 0,0 à 1,0 dans l'exemple de réseau ci-dessus. Les exemples suivants montrent des exemples de telles fonctions d'étalonnage avec 10 points clés :


C'est souvent une bonne idée d'utiliser les quantiles des caractéristiques comme points clés d'entrée. Les modèles prédéfinis TensorFlow Lattice peuvent définir automatiquement les points clés d'entrée sur les quantiles de caractéristiques.
Pour les fonctionnalités catégorielles, TensorFlow Lattice fournit un étalonnage catégoriel (avec tfl.layers.CategoricalCalibration ) avec une limite de sortie similaire à alimenter dans un réseau.
Ensembles
Le nombre de paramètres d'une couche de réseau augmente de façon exponentielle avec le nombre d'entités en entrée, ce qui ne s'adapte donc pas bien aux dimensions très élevées. Pour surmonter cette limitation, TensorFlow Lattice propose des ensembles de réseaux qui combinent (en moyenne) plusieurs petits réseaux, ce qui permet au modèle de croître linéairement en nombre de fonctionnalités.
La bibliothèque propose deux variantes de ces ensembles :
Random Tiny Lattices (RTL) : chaque sous-modèle utilise un sous-ensemble aléatoire de fonctionnalités (avec remplacement).
Crystals : l'algorithme Crystals entraîne d'abord un modèle de préajustement qui estime les interactions de fonctionnalités par paires. Il organise ensuite l'ensemble final de telle sorte que les entités ayant davantage d'interactions non linéaires se trouvent dans les mêmes réseaux.
Pourquoi le treillis TensorFlow ?
Vous pouvez trouver une brève introduction à TensorFlow Lattice dans cet article du blog TF .
Interprétabilité
Étant donné que les paramètres de chaque couche sont la sortie de cette couche, il est facile d'analyser, de comprendre et de déboguer chaque partie du modèle.
Modèles précis et flexibles
En utilisant des réseaux à grain fin, vous pouvez obtenir des fonctions arbitrairement complexes avec une seule couche de réseau. L'utilisation de plusieurs couches de calibrateurs et de réseaux fonctionne souvent bien dans la pratique et peut correspondre ou surpasser les modèles DNN de tailles similaires.
Contraintes de forme de bon sens
Les données d'entraînement réelles peuvent ne pas représenter suffisamment les données d'exécution. Les solutions de ML flexibles telles que les DNN ou les forêts agissent souvent de manière inattendue, voire sauvage, dans des parties de l'espace d'entrée non couvertes par les données d'entraînement. Ce comportement est particulièrement problématique lorsque les contraintes politiques ou d’équité peuvent être violées.

Même si les formes courantes de régularisation peuvent aboutir à une extrapolation plus judicieuse, les régularisateurs standards ne peuvent pas garantir un comportement raisonnable du modèle dans l'ensemble de l'espace d'entrée, en particulier avec des entrées de grande dimension. Le passage à des modèles plus simples avec un comportement plus contrôlé et prévisible peut avoir un coût important en termes de précision du modèle.
TF Lattice permet de continuer à utiliser des modèles flexibles, mais offre plusieurs options pour injecter des connaissances du domaine dans le processus d'apprentissage à travers des contraintes de forme sémantiquement significatives ou motivées par des politiques :
- Monotonie : Vous pouvez spécifier que la sortie ne doit augmenter/diminuer que par rapport à une entrée. Dans notre exemple, vous souhaiterez peut-être spécifier que l'augmentation de la distance jusqu'à un café ne devrait que diminuer la préférence prévue de l'utilisateur.




Convexité/Concavité : Vous pouvez spécifier que la forme de la fonction peut être convexe ou concave. Mélangé à la monotonie, cela peut forcer la fonction à représenter des rendements décroissants par rapport à une caractéristique donnée.
Unimodalité : Vous pouvez spécifier que la fonction doit avoir un pic ou une vallée unique. Cela vous permet de représenter des fonctions qui ont un point idéal par rapport à une fonctionnalité.
Confiance par paire : cette contrainte fonctionne sur une paire de fonctionnalités et suggère qu'une fonctionnalité d'entrée reflète sémantiquement la confiance dans une autre fonctionnalité. Par exemple, un nombre plus élevé d’avis vous rend plus confiant dans la note moyenne d’un restaurant. Le modèle sera plus sensible par rapport à la note par étoiles (c'est-à-dire aura une pente plus grande par rapport à la note) lorsque le nombre d'avis est plus élevé.
Flexibilité contrôlée avec les régularisateurs
En plus des contraintes de forme, le treillis TensorFlow fournit un certain nombre de régularisateurs pour contrôler la flexibilité et la fluidité de la fonction pour chaque couche.
Régulateur laplacien : les sorties du réseau/sommets de calibrage/points clés sont régularisées vers les valeurs de leurs voisins respectifs. Il en résulte une fonction plus plate .
Hessian Regularizer : Cela pénalise la dérivée première de la couche d'étalonnage PWL pour rendre la fonction plus linéaire .
Wrinkle Regularizer : Ceci pénalise la dérivée seconde de la couche de calibrage PWL pour éviter des changements brusques de courbure. Cela rend la fonction plus fluide.
Régulateur de torsion : les sorties du réseau seront régularisées pour empêcher la torsion entre les entités. En d’autres termes, le modèle sera régularisé vers l’indépendance entre les contributions des fonctionnalités.
Mélangez et assortissez avec d'autres couches Keras
Vous pouvez utiliser les couches TF Lattice en combinaison avec d'autres couches Keras pour construire des modèles partiellement contraints ou régularisés. Par exemple, des couches d'étalonnage de réseau ou PWL peuvent être utilisées au niveau de la dernière couche de réseaux plus profonds qui incluent des intégrations ou d'autres couches Keras.
Papiers
- Éthique déontologique par contraintes de forme monotonique , Serena Wang, Maya Gupta, Conférence internationale sur l'intelligence artificielle et les statistiques (AISSTATS), 2020
- Contraintes de forme pour les fonctions d'ensemble , Andrew Cotter, Maya Gupta, H. Jiang, Erez Louidor, Jim Muller, Taman Narayan, Serena Wang, Tao Zhu. Conférence internationale sur l'apprentissage automatique (ICML), 2019
- Les rendements décroissants façonnent les contraintes d'interprétabilité et de régularisation , Maya Gupta, Dara Bahri, Andrew Cotter, Kevin Canini, Advances in Neural Information Processing Systems (NeurIPS), 2018
- Réseaux à treillis profonds et fonctions monotoniques partielles , Seungil You, Kevin Canini, David Ding, Jan Pfeifer, Maya R. Gupta, Advances in Neural Information Processing Systems (NeurIPS), 2017
- Fonctions monotones rapides et flexibles avec des ensembles de réseaux , Mahdi Milani Fard, Kevin Canini, Andrew Cotter, Jan Pfeifer, Maya Gupta, Advances in Neural Information Processing Systems (NeurIPS), 2016
- Tables de recherche interpolées calibrées monotones , Maya Gupta, Andrew Cotter, Jan Pfeifer, Konstantin Voevodski, Kevin Canini, Alexander Mangylov, Wojciech Moczydlowski, Alexander van Esbroeck, Journal of Machine Learning Research (JMLR), 2016
- Régression optimisée pour une évaluation efficace des fonctions , Eric Garcia, Raman Arora, Maya R. Gupta, IEEE Transactions on Image Processing, 2012
- Régression sur réseau , Eric Garcia, Maya Gupta, Advances in Neural Information Processing Systems (NeurIPS), 2009
Tutoriels et documents API
Pour les architectures de modèles courantes, vous pouvez utiliser des modèles prédéfinis Keras . Vous pouvez également créer des modèles personnalisés à l’aide des calques TF Lattice Keras ou les mélanger avec d’autres calques Keras. Consultez la documentation complète de l'API pour plus de détails.

