 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Neste colab, vamos explorar a amostragem da parte posterior de um modelo de mistura gaussiana bayesiana (BGMM) usando apenas primitivas de probabilidade TensorFlow.
Modelo
Para \(k\in\{1,\ldots, K\}\) componentes da mistura de cada um de dimensão \(D\), gostaríamos de modelo \(i\in\{1,\ldots,N\}\) amostras usando o seguinte modelo de mistura Gaussiana de Bayesian iid:
\[\begin{align*} \theta &\sim \text{Dirichlet}(\text{concentration}=\alpha_0)\\ \mu_k &\sim \text{Normal}(\text{loc}=\mu_{0k}, \text{scale}=I_D)\\ T_k &\sim \text{Wishart}(\text{df}=5, \text{scale}=I_D)\\ Z_i &\sim \text{Categorical}(\text{probs}=\theta)\\ Y_i &\sim \text{Normal}(\text{loc}=\mu_{z_i}, \text{scale}=T_{z_i}^{-1/2})\\ \end{align*}\]
Note, os scale argumentos todos têm cholesky semântica. Usamos essa convenção porque é a das Distribuições TF (que por sua vez usa essa convenção em parte porque é computacionalmente vantajosa).
Nosso objetivo é gerar amostras a partir da parte posterior:
\[p\left(\theta, \{\mu_k, T_k\}_{k=1}^K \Big| \{y_i\}_{i=1}^N, \alpha_0, \{\mu_{ok}\}_{k=1}^K\right)\]
Observe que \(\{Z_i\}_{i=1}^N\) não está presente - estamos interessados em apenas as variáveis aleatórias que não escalam com \(N\). (E felizmente há uma distribuição TF que lida com marginalizando a \(Z_i\).)
Não é possível obter amostras diretamente dessa distribuição devido a um termo de normalização intratável computacionalmente.
Algoritmos de Metropolis-Hastings são técnica para a amostragem a partir de distribuições intratáveis-se normalizar.
O TensorFlow Probability oferece várias opções de MCMC, incluindo várias baseadas em Metropolis-Hastings. Neste caderno, usaremos Hamiltonian Monte Carlo ( tfp.mcmc.HamiltonianMonteCarlo ). O HMC costuma ser uma boa escolha porque pode convergir rapidamente, amostrar o espaço de estado em conjunto (em vez de coordenar) e alavancar uma das virtudes do TF: diferenciação automática. Dito isto, a amostragem de um posterior BGMM pode realmente ser melhor feito por outras abordagens, por exemplo, de amostragem de Gibb .
%matplotlib inline
import functools
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import seaborn as sns; sns.set_context('notebook')
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
physical_devices = tf.config.experimental.list_physical_devices('GPU')
if len(physical_devices) > 0:
tf.config.experimental.set_memory_growth(physical_devices[0], True)
Antes de realmente construir o modelo, precisaremos definir um novo tipo de distribuição. A partir da especificação do modelo acima, fica claro que estamos parametrizando o MVN com uma matriz de covariância inversa, ou seja, [matriz de precisão] (https://en.wikipedia.org/wiki/Precision_ (estatísticas% 29). Para fazer isso em TF, vamos precisar rolar a nossa Bijector Este. Bijector usará a transformação para a frente:
-
Y = tf.linalg.triangular_solve((tf.linalg.matrix_transpose(chol_precision_tril), X, adjoint=True) + loc.
E o log_prob cálculo é apenas o inverso, ou seja:
-
X = tf.linalg.matmul(chol_precision_tril, X - loc, adjoint_a=True).
Uma vez que todos necessidade que para HMC é log_prob , isso significa que evitar sempre chamando tf.linalg.triangular_solve (como seria o caso para tfd.MultivariateNormalTriL ). Isto é vantajoso uma vez tf.linalg.matmul geralmente é mais rápido devido à melhor localidade cache.
class MVNCholPrecisionTriL(tfd.TransformedDistribution):
"""MVN from loc and (Cholesky) precision matrix."""
def __init__(self, loc, chol_precision_tril, name=None):
super(MVNCholPrecisionTriL, self).__init__(
distribution=tfd.Independent(tfd.Normal(tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=chol_precision_tril,
adjoint=True)),
]),
name=name)
O tfd.Independent curvas de distribuição independente chama de uma distribuição, num distribuição multivariada com coordenadas estatisticamente independentes. Em termos de computação log_prob , este manifesta "meta-distribuição", como uma soma simples sobre a dimensão (s) evento.
Note também que tomamos a adjoint ( "transposição") da matriz escala. Isto é porque se a precisão é covariância inversa, ou seja, \(P=C^{-1}\) e se \(C=AA^\top\), então \(P=BB^{\top}\) onde \(B=A^{-\top}\).
Desde essa distribuição é uma espécie de complicado, vamos verificar rapidamente se o nosso MVNCholPrecisionTriL funciona como pensamos que deveria.
def compute_sample_stats(d, seed=42, n=int(1e6)):
x = d.sample(n, seed=seed)
sample_mean = tf.reduce_mean(x, axis=0, keepdims=True)
s = x - sample_mean
sample_cov = tf.linalg.matmul(s, s, adjoint_a=True) / tf.cast(n, s.dtype)
sample_scale = tf.linalg.cholesky(sample_cov)
sample_mean = sample_mean[0]
return [
sample_mean,
sample_cov,
sample_scale,
]
dtype = np.float32
true_loc = np.array([1., -1.], dtype=dtype)
true_chol_precision = np.array([[1., 0.],
[2., 8.]],
dtype=dtype)
true_precision = np.matmul(true_chol_precision, true_chol_precision.T)
true_cov = np.linalg.inv(true_precision)
d = MVNCholPrecisionTriL(
loc=true_loc,
chol_precision_tril=true_chol_precision)
[sample_mean, sample_cov, sample_scale] = [
t.numpy() for t in compute_sample_stats(d)]
print('true mean:', true_loc)
print('sample mean:', sample_mean)
print('true cov:\n', true_cov)
print('sample cov:\n', sample_cov)
true mean: [ 1. -1.] sample mean: [ 1.0002806 -1.000105 ] true cov: [[ 1.0625 -0.03125 ] [-0.03125 0.015625]] sample cov: [[ 1.0641273 -0.03126175] [-0.03126175 0.01559312]]
Como a média e a covariância da amostra estão próximas da média e da covariância verdadeiras, parece que a distribuição está implementada corretamente. Agora, vamos usar MVNCholPrecisionTriL tfp.distributions.JointDistributionNamed para especificar o modelo BGMM. Para o modelo de observação, usaremos tfd.MixtureSameFamily para integrar automaticamente o \(\{Z_i\}_{i=1}^N\) empates.
dtype = np.float64
dims = 2
components = 3
num_samples = 1000
bgmm = tfd.JointDistributionNamed(dict(
mix_probs=tfd.Dirichlet(
concentration=np.ones(components, dtype) / 10.),
loc=tfd.Independent(
tfd.Normal(
loc=np.stack([
-np.ones(dims, dtype),
np.zeros(dims, dtype),
np.ones(dims, dtype),
]),
scale=tf.ones([components, dims], dtype)),
reinterpreted_batch_ndims=2),
precision=tfd.Independent(
tfd.WishartTriL(
df=5,
scale_tril=np.stack([np.eye(dims, dtype=dtype)]*components),
input_output_cholesky=True),
reinterpreted_batch_ndims=1),
s=lambda mix_probs, loc, precision: tfd.Sample(tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(probs=mix_probs),
components_distribution=MVNCholPrecisionTriL(
loc=loc,
chol_precision_tril=precision)),
sample_shape=num_samples)
))
def joint_log_prob(observations, mix_probs, loc, chol_precision):
"""BGMM with priors: loc=Normal, precision=Inverse-Wishart, mix=Dirichlet.
Args:
observations: `[n, d]`-shaped `Tensor` representing Bayesian Gaussian
Mixture model draws. Each sample is a length-`d` vector.
mix_probs: `[K]`-shaped `Tensor` representing random draw from
`Dirichlet` prior.
loc: `[K, d]`-shaped `Tensor` representing the location parameter of the
`K` components.
chol_precision: `[K, d, d]`-shaped `Tensor` representing `K` lower
triangular `cholesky(Precision)` matrices, each being sampled from
a Wishart distribution.
Returns:
log_prob: `Tensor` representing joint log-density over all inputs.
"""
return bgmm.log_prob(
mix_probs=mix_probs, loc=loc, precision=chol_precision, s=observations)
Gerar dados de "treinamento"
Para esta demonstração, vamos amostrar alguns dados aleatórios.
true_loc = np.array([[-2., -2],
[0, 0],
[2, 2]], dtype)
random = np.random.RandomState(seed=43)
true_hidden_component = random.randint(0, components, num_samples)
observations = (true_loc[true_hidden_component] +
random.randn(num_samples, dims).astype(dtype))
Inferência Bayesiana usando HMC
Agora que usamos TFD para especificar nosso modelo e obtivemos alguns dados observados, temos todas as peças necessárias para executar o HMC.
Para fazer isso, vamos utilizar uma aplicação parcial com "pin down" as coisas que não querem amostra. Neste caso, isso significa que só precisa de definir observations . (Os hiper-parâmetros já são cozidos em distribuições para os anteriores e que não faz parte do joint_log_prob assinatura função).
unnormalized_posterior_log_prob = functools.partial(joint_log_prob, observations)
initial_state = [
tf.fill([components],
value=np.array(1. / components, dtype),
name='mix_probs'),
tf.constant(np.array([[-2., -2],
[0, 0],
[2, 2]], dtype),
name='loc'),
tf.linalg.eye(dims, batch_shape=[components], dtype=dtype, name='chol_precision'),
]
Representação Irrestrita
O Hamiltoniano Monte Carlo (HMC) requer que a função de log-probabilidade de destino seja diferenciável com relação a seus argumentos. Além disso, o HMC pode exibir eficiência estatística dramaticamente maior se o espaço de estado não for restringido.
Isso significa que teremos que resolver dois problemas principais ao amostrar a partir da parte posterior do BGMM:
- \(\theta\) representa um vector de probabilidade discreta, isto é, deve ser tal que \(\sum_{k=1}^K \theta_k = 1\) e \(\theta_k>0\).
- \(T_k\) representa uma matriz de covariância inversa, ou seja, deve ser tal que \(T_k \succ 0\), isto é, é definida positiva .
Para atender a esse requisito, precisaremos:
- transformar as variáveis restritas em um espaço irrestrito
- execute o MCMC em espaço irrestrito
- transforme as variáveis irrestritas de volta ao espaço restrito.
Tal como acontece com MVNCholPrecisionTriL , usaremos Bijector s para transformar variáveis aleatórias para o espaço sem restrições.
O
Dirichleté transformado para o espaço sem restrições através da função Softmax .Nossa variável aleatória de precisão é uma distribuição sobre matrizes semidefinidas positivas. Para Libertar estes usaremos os
FillTriangulareTransformDiagonalbijectors. Esses vetores convertem em matrizes triangulares inferiores e garantem que a diagonal seja positiva. O primeiro é útil porque permite a amostragem única \(d(d+1)/2\) flutua em vez de \(d^2\).
unconstraining_bijectors = [
tfb.SoftmaxCentered(),
tfb.Identity(),
tfb.Chain([
tfb.TransformDiagonal(tfb.Softplus()),
tfb.FillTriangular(),
])]
@tf.function(autograph=False)
def sample():
return tfp.mcmc.sample_chain(
num_results=2000,
num_burnin_steps=500,
current_state=initial_state,
kernel=tfp.mcmc.SimpleStepSizeAdaptation(
tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unnormalized_posterior_log_prob,
step_size=0.065,
num_leapfrog_steps=5),
bijector=unconstraining_bijectors),
num_adaptation_steps=400),
trace_fn=lambda _, pkr: pkr.inner_results.inner_results.is_accepted)
[mix_probs, loc, chol_precision], is_accepted = sample()
Agora vamos executar a cadeia e imprimir os meios posteriores.
acceptance_rate = tf.reduce_mean(tf.cast(is_accepted, dtype=tf.float32)).numpy()
mean_mix_probs = tf.reduce_mean(mix_probs, axis=0).numpy()
mean_loc = tf.reduce_mean(loc, axis=0).numpy()
mean_chol_precision = tf.reduce_mean(chol_precision, axis=0).numpy()
precision = tf.linalg.matmul(chol_precision, chol_precision, transpose_b=True)
print('acceptance_rate:', acceptance_rate)
print('avg mix probs:', mean_mix_probs)
print('avg loc:\n', mean_loc)
print('avg chol(precision):\n', mean_chol_precision)
acceptance_rate: 0.5305 avg mix probs: [0.25248723 0.60729516 0.1402176 ] avg loc: [[-1.96466753 -2.12047249] [ 0.27628865 0.22944732] [ 2.06461244 2.54216122]] avg chol(precision): [[[ 1.05105032 0. ] [ 0.12699955 1.06553113]] [[ 0.76058015 0. ] [-0.50332767 0.77947431]] [[ 1.22770457 0. ] [ 0.70670027 1.50914164]]]
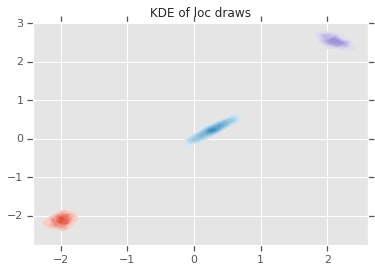
loc_ = loc.numpy()
ax = sns.kdeplot(loc_[:,0,0], loc_[:,0,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,1,0], loc_[:,1,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,2,0], loc_[:,2,1], shade=True, shade_lowest=False)
plt.title('KDE of loc draws');
Conclusão
Este colab simples demonstrou como as primitivas de probabilidade do TensorFlow podem ser usadas para construir modelos hierárquicos de mistura bayesiana.
