Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Ce réimplémente bloc - notes et étend la « analyse des points changement » bayésienne exemple de la documentation pymc3 .
Conditions préalables
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (15,8)
%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
Base de données
L'ensemble de données est d' ici . Remarque, il existe une autre version de cet exemple flottant autour , mais il a « disparu » des données - dans ce cas , vous aurez besoin d'imputer les valeurs manquantes. (Sinon, votre modèle ne quittera jamais ses paramètres initiaux car la fonction de vraisemblance ne sera pas définie.)
disaster_data = np.array([ 4, 5, 4, 0, 1, 4, 3, 4, 0, 6, 3, 3, 4, 0, 2, 6,
3, 3, 5, 4, 5, 3, 1, 4, 4, 1, 5, 5, 3, 4, 2, 5,
2, 2, 3, 4, 2, 1, 3, 2, 2, 1, 1, 1, 1, 3, 0, 0,
1, 0, 1, 1, 0, 0, 3, 1, 0, 3, 2, 2, 0, 1, 1, 1,
0, 1, 0, 1, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0, 2,
3, 3, 1, 1, 2, 1, 1, 1, 1, 2, 4, 2, 0, 0, 1, 4,
0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1])
years = np.arange(1851, 1962)
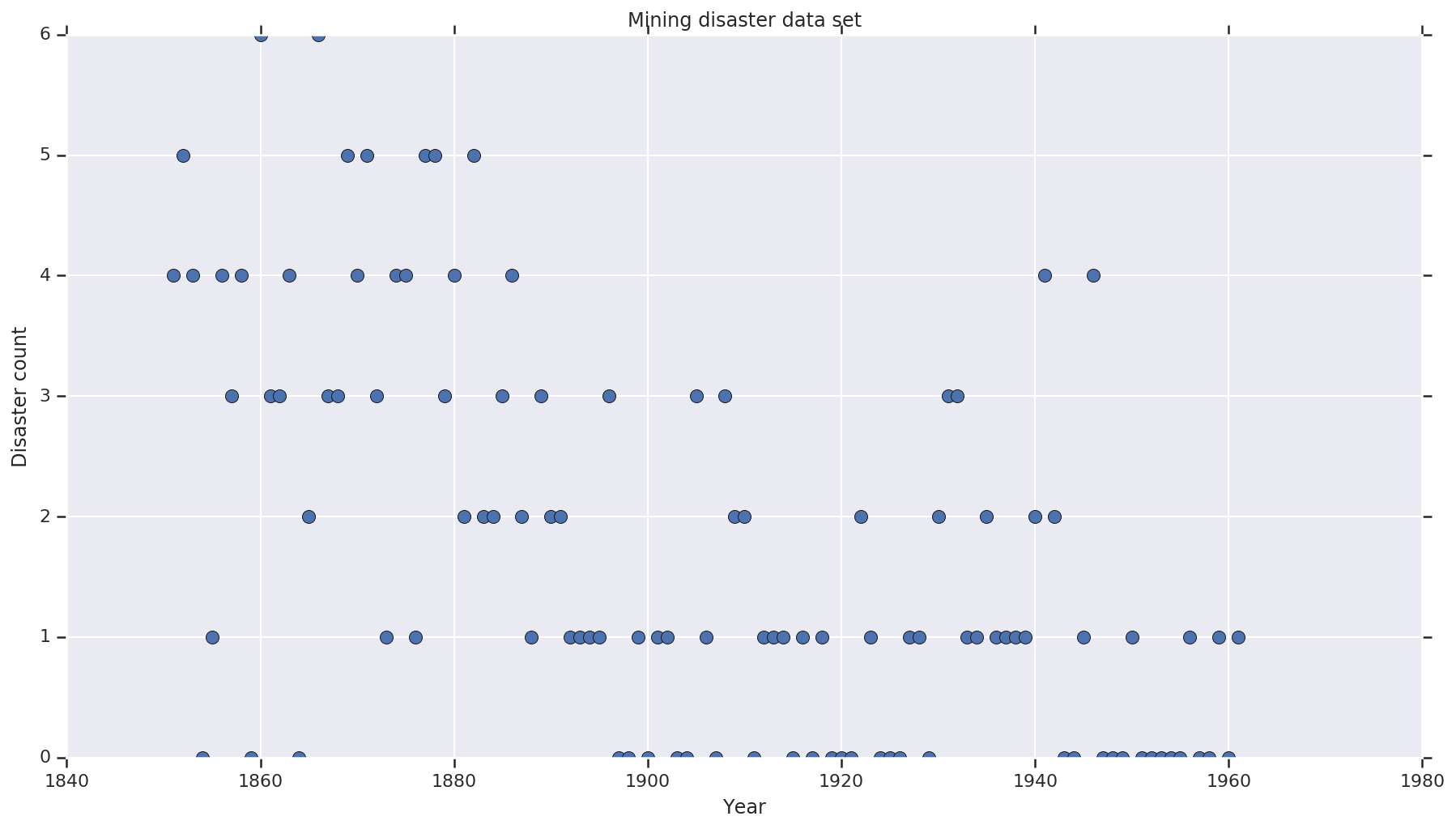
plt.plot(years, disaster_data, 'o', markersize=8);
plt.ylabel('Disaster count')
plt.xlabel('Year')
plt.title('Mining disaster data set')
plt.show()
Modèle probabiliste
Le modèle suppose un « point de commutation » (par exemple, une année au cours de laquelle les règles de sécurité ont changé) et un taux de catastrophe selon la loi de Poisson avec des taux constants (mais potentiellement différents) avant et après ce point de commutation.
Le nombre réel de catastrophes est fixe (observé) ; tout échantillon de ce modèle devra spécifier à la fois le point de commutation et le taux « précoce » et « tardif » de catastrophes.
Modèle original d' exemple de documentation pymc3 :
\[ \begin{align*} (D_t|s,e,l)&\sim \text{Poisson}(r_t), \\ & \,\quad\text{with}\; r_t = \begin{cases}e & \text{if}\; t < s\\l &\text{if}\; t \ge s\end{cases} \\ s&\sim\text{Discrete Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
Cependant, le taux de catastrophe moyen \(r_t\) a une discontinuité au point de coupure \(s\), ce qui le rend pas différentiables. Ainsi , il ne fournit aucun signal de gradient à l'algorithme Monte Carlo hamiltonien (HMC) - mais parce que le \(s\) est antérieure continue, le repli à une marche aléatoire de HMC est assez bon pour trouver les zones de masse à haute probabilité dans cet exemple.
Dans un deuxième modèle, on modifie le modèle d' origine en utilisant une sigmoïde « switch » entre E et L pour faire la transition dérivable, et en utilisant une distribution uniforme continue pour le point de commutation \(s\). (On pourrait soutenir que ce modèle est plus fidèle à la réalité, car un « changement » du taux moyen serait probablement étalé sur plusieurs années.) Le nouveau modèle est donc :
\[ \begin{align*} (D_t|s,e,l)&\sim\text{Poisson}(r_t), \\ & \,\quad \text{with}\; r_t = e + \frac{1}{1+\exp(s-t)}(l-e) \\ s&\sim\text{Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
En l'absence de plus d' informations que nous supposons \(r_e = r_l = 1\) en tant que paramètres pour les prieurs. Nous exécuterons les deux modèles et comparerons leurs résultats d'inférence.
def disaster_count_model(disaster_rate_fn):
disaster_count = tfd.JointDistributionNamed(dict(
e=tfd.Exponential(rate=1.),
l=tfd.Exponential(rate=1.),
s=tfd.Uniform(0., high=len(years)),
d_t=lambda s, l, e: tfd.Independent(
tfd.Poisson(rate=disaster_rate_fn(np.arange(len(years)), s, l, e)),
reinterpreted_batch_ndims=1)
))
return disaster_count
def disaster_rate_switch(ys, s, l, e):
return tf.where(ys < s, e, l)
def disaster_rate_sigmoid(ys, s, l, e):
return e + tf.sigmoid(ys - s) * (l - e)
model_switch = disaster_count_model(disaster_rate_switch)
model_sigmoid = disaster_count_model(disaster_rate_sigmoid)
Le code ci-dessus définit le modèle via des distributions JointDistributionSequential. Les disaster_rate fonctions sont appelées avec un tableau de [0, ..., len(years)-1] pour produire un vecteur de len(years) variables aléatoires - les années précédant le point de switchpoint sont early_disaster_rate , les uns après late_disaster_rate (modulo la transition sigmoïde).
Voici une vérification de l'intégrité que la fonction de prob de journal cible est saine :
def target_log_prob_fn(model, s, e, l):
return model.log_prob(s=s, e=e, l=l, d_t=disaster_data)
models = [model_switch, model_sigmoid]
print([target_log_prob_fn(m, 40., 3., .9).numpy() for m in models]) # Somewhat likely result
print([target_log_prob_fn(m, 60., 1., 5.).numpy() for m in models]) # Rather unlikely result
print([target_log_prob_fn(m, -10., 1., 1.).numpy() for m in models]) # Impossible result
[-176.94559, -176.28717] [-371.3125, -366.8816] [-inf, -inf]
HMC pour faire l'inférence bayésienne
Nous définissons le nombre de résultats et d'étapes de rodage nécessaires ; le code est modélisé principalement après la documentation de tfp.mcmc.HamiltonianMonteCarlo . Il utilise une taille de pas adaptative (sinon le résultat est très sensible à la valeur de taille de pas choisie). Nous utilisons des valeurs de un comme état initial de la chaîne.
Ce n'est pas toute l'histoire cependant. Si vous revenez à la définition du modèle ci-dessus, vous remarquerez que certaines des distributions de probabilité ne sont pas bien définies sur toute la droite des nombres réels. Par conséquent , nous limitons l'espace HMC examine en enveloppant le noyau de la console HMC avec un TransformedTransitionKernel qui spécifie les bijectors avant de transformer les nombres réels sur le domaine que la distribution de probabilité est définie sur (voir les commentaires dans le code ci - dessous).
num_results = 10000
num_burnin_steps = 3000
@tf.function(autograph=False, jit_compile=True)
def make_chain(target_log_prob_fn):
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.05,
num_leapfrog_steps=3),
bijector=[
# The switchpoint is constrained between zero and len(years).
# Hence we supply a bijector that maps the real numbers (in a
# differentiable way) to the interval (0;len(yers))
tfb.Sigmoid(low=0., high=tf.cast(len(years), dtype=tf.float32)),
# Early and late disaster rate: The exponential distribution is
# defined on the positive real numbers
tfb.Softplus(),
tfb.Softplus(),
])
kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=int(0.8*num_burnin_steps))
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
# The three latent variables
tf.ones([], name='init_switchpoint'),
tf.ones([], name='init_early_disaster_rate'),
tf.ones([], name='init_late_disaster_rate'),
],
trace_fn=None,
kernel=kernel)
return states
switch_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_switch, *args))]
sigmoid_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_sigmoid, *args))]
switchpoint, early_disaster_rate, late_disaster_rate = zip(
switch_samples, sigmoid_samples)
Exécutez les deux modèles en parallèle :
Visualisez le résultat
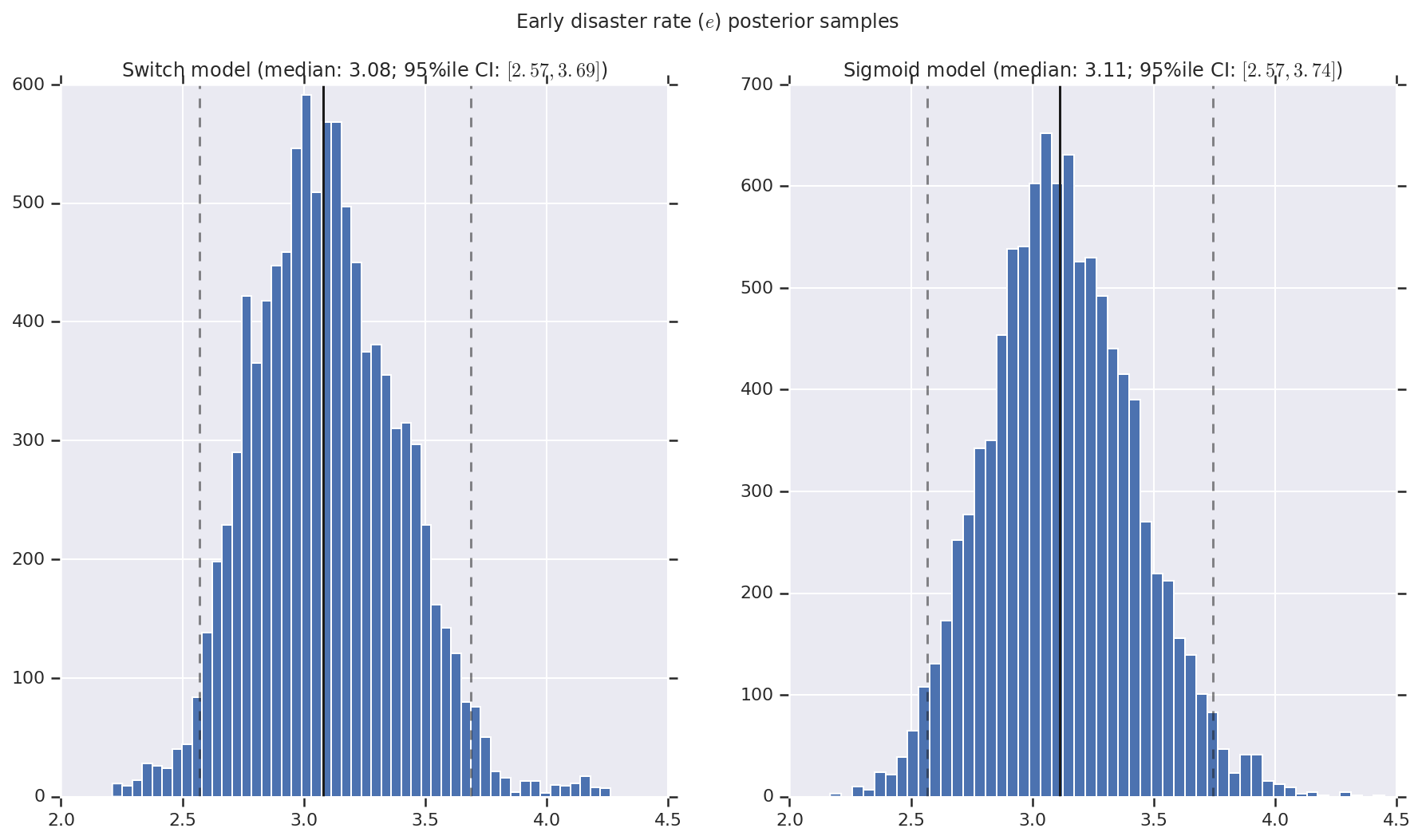
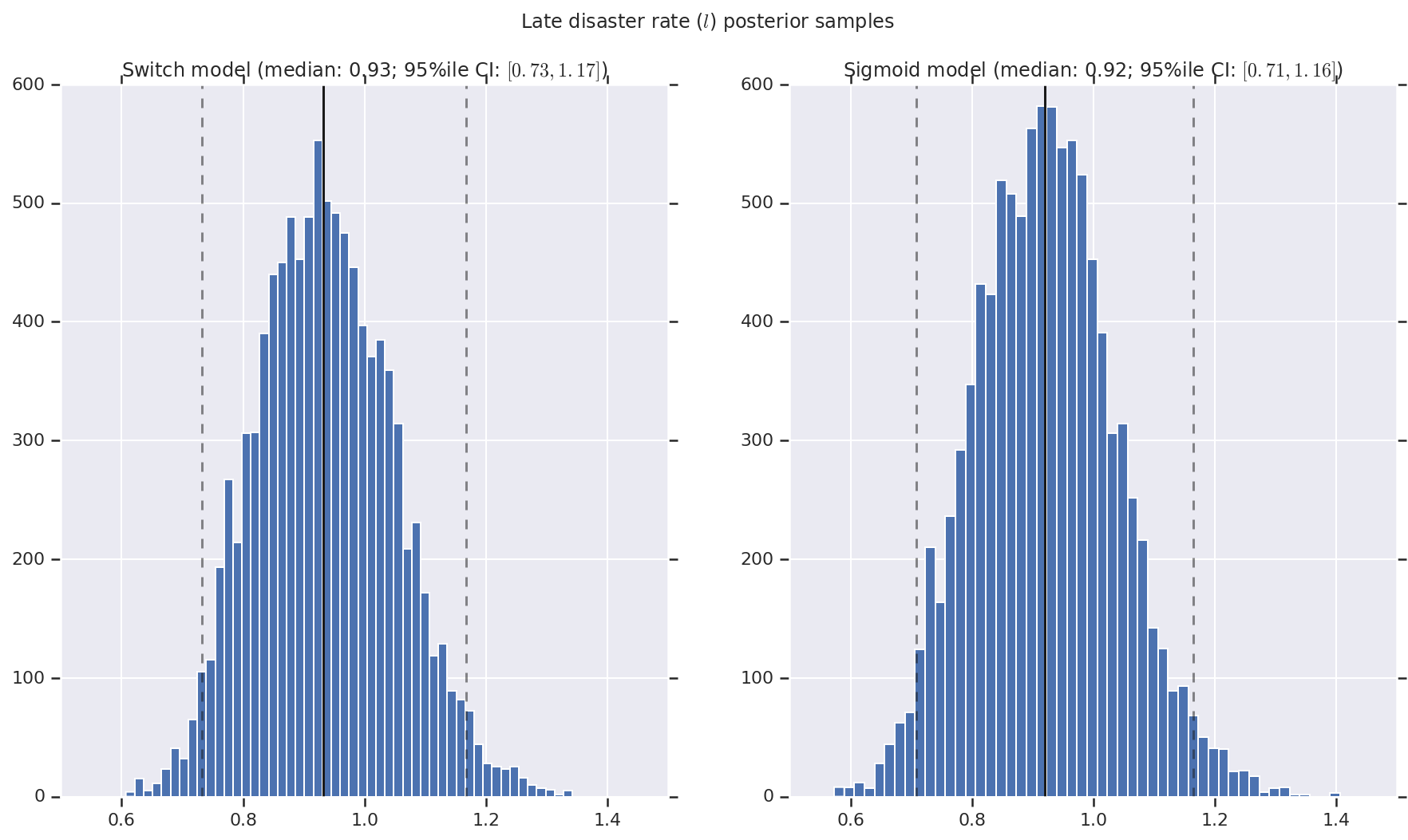
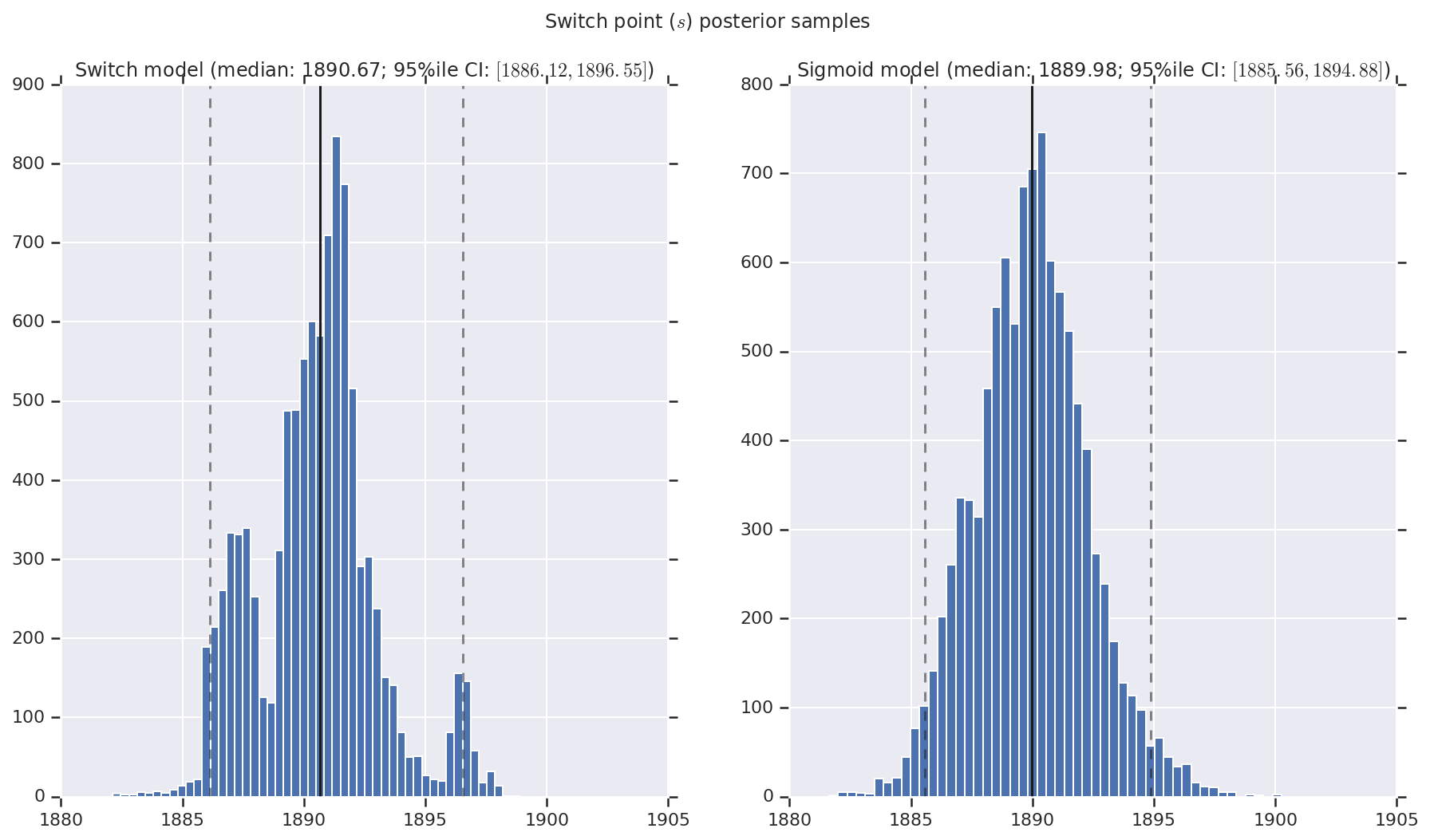
Nous visualisons le résultat sous forme d'histogrammes d'échantillons de la distribution postérieure pour le taux de catastrophe précoce et tardif, ainsi que le point de commutation. Les histogrammes sont recouverts d'une ligne continue représentant la médiane de l'échantillon, ainsi que les limites de l'intervalle de crédibilité à 95 % des iles sous forme de lignes en pointillés.
def _desc(v):
return '(median: {}; 95%ile CI: $[{}, {}]$)'.format(
*np.round(np.percentile(v, [50, 2.5, 97.5]), 2))
for t, v in [
('Early disaster rate ($e$) posterior samples', early_disaster_rate),
('Late disaster rate ($l$) posterior samples', late_disaster_rate),
('Switch point ($s$) posterior samples', years[0] + switchpoint),
]:
fig, ax = plt.subplots(nrows=1, ncols=2, sharex=True)
for (m, i) in (('Switch', 0), ('Sigmoid', 1)):
a = ax[i]
a.hist(v[i], bins=50)
a.axvline(x=np.percentile(v[i], 50), color='k')
a.axvline(x=np.percentile(v[i], 2.5), color='k', ls='dashed', alpha=.5)
a.axvline(x=np.percentile(v[i], 97.5), color='k', ls='dashed', alpha=.5)
a.set_title(m + ' model ' + _desc(v[i]))
fig.suptitle(t)
plt.show()