Modelowanie rozprzestrzeniania się COVID-19 w Europie i efekt interwencji

Licencjonowane na podstawie licencji MIT

Zobacz na TensorFlow.org Uruchom w Google Colab Wyświetl źródło na GitHub Pobierz notatnik

Aby spowolnić rozprzestrzenianie się COVID-19 na początku 2020 r., kraje europejskie przyjęły interwencje pozafarmaceutyczne, takie jak zamykanie nieistotnych firm, izolacja indywidualnych przypadków, zakaz podróżowania i inne środki zachęcające do zdystansowania społecznego. Zespół Imperial College COVID-19 odpowiedzi analizowano skuteczność tych środków w swoim artykule „Oszacowanie liczby zakażeń i wpływu interwencji niefarmaceutycznymi na COVID-19 w 11 krajach europejskich” , używając Bayesa hierarchiczny model w połączeniu z mechanistyczny model epidemiologiczny.

Ten Colab zawiera implementację tej analizy TensorFlow Probability (TFP), zorganizowaną w następujący sposób:

  • „Konfiguracja modelu” definiuje model epidemiologiczny przenoszenia choroby i wynikających z niej zgonów, rozkład bayesowski w stosunku do parametrów modelu oraz rozkład liczby zgonów w zależności od wartości parametrów.
  • „Wstępne przetwarzanie danych” ładuje dane dotyczące czasu i rodzaju interwencji w każdym kraju, liczby zgonów w czasie oraz szacunkowych wskaźników śmiertelności wśród osób zakażonych.
  • „Wnioskowanie o modelu” buduje hierarchiczny model bayesowski i uruchamia hamiltonian Monte Carlo (HMC) w celu pobrania próbki z rozkładu a posteriori parametrów.
  • „Wyniki” pokazują rozkłady predykcyjne a posteriori dla ilości będących przedmiotem zainteresowania, takich jak przewidywane zgony i zgony kontrfaktyczne w przypadku braku interwencji.

Papier znaleźli dowody, że kraje udało się zmniejszyć liczbę nowych zakażeń przenoszonych przez poszczególne osoby zakażonej (\(R_t\)), ale to wiarygodne przedziały zawarte \(R_t=1\) (wartość powyżej której epidemia nadal się rozprzestrzenia) i że była przedwczesna wyciąganie mocnych wniosków na temat skuteczności interwencji. Kod Stan na papierze jest w autorów GitHub repozytorium, a to Colab odtwarza Version 2 .

pip3 install -q git+git://github.com/arviz-devs/arviz.git
pip3 install -q tf-nightly tfp-nightly

Import

1 Konfiguracja modelu

1.1 Mechaniczny model infekcji i zgonów

Model infekcji symuluje liczbę infekcji w każdym kraju w czasie. Dane wejściowe to czas i rodzaj interwencji, wielkość populacji i początkowe przypadki. Parametry kontrolują skuteczność interwencji i szybkość przenoszenia chorób. Model oczekiwanej liczby zgonów stosuje wskaźnik śmiertelności do przewidywanych infekcji.

Model infekcji wykonuje splot poprzednich codziennych infekcji z szeregowym rozkładem interwałów (rozkład w ciągu liczby dni między zarażeniem a zarażeniem kogoś innego). Na każdym kroku czasowym ilość nowe zakażenia w czasie \(t\), \(n_t\), obliczonego

\begin{equation} \sum_{i=0}^{t-1} n_i \mu_t \text{p} (\text{złapany od kogoś zarażonego w } i | \text{nowo zarażony w } t) \end{ równanie} gdzie \(\mu_t=R_t\) i prawdopodobieństwa warunkowego jest przechowywany w conv_serial_interval określone poniżej.

Model oczekiwanych zgonów przedstawia splot codziennych infekcji i rozkład dni między infekcją a zgonem. Oznacza to, że oczekiwane zgonów na dzień \(t\) jest obliczana jako

\ rozpocząć {równanie} \ sum_ {i = 0} ^ {t-1} n_i \ tekstu {p (śmierci na dzień \(t\)| zakażenia na dzień \(i\))} \ koniec {równanie} gdzie zapisany jest prawdopodobieństwa warunkowego w conv_fatality_rate określone poniżej.

from tensorflow_probability.python.internal import broadcast_util as bu

def predict_infections(
    intervention_indicators, population, initial_cases, mu, alpha_hier,
    conv_serial_interval, initial_days, total_days):
  """Predict the number of infections by forward-simulation.

  Args:
    intervention_indicators: Binary array of shape
      `[num_countries, total_days, num_interventions]`, in which `1` indicates
      the intervention is active in that country at that time and `0` indicates
      otherwise.
    population: Vector of length `num_countries`. Population of each country.
    initial_cases: Array of shape `[batch_size, num_countries]`. Number of cases
      in each country at the start of the simulation.
    mu: Array of shape `[batch_size, num_countries]`. Initial reproduction rate
      (R_0) by country.
    alpha_hier: Array of shape `[batch_size, num_interventions]` representing
      the effectiveness of interventions.
    conv_serial_interval: Array of shape
      `[total_days - initial_days, total_days]` output from
      `make_conv_serial_interval`. Convolution kernel for serial interval
      distribution.
    initial_days: Integer, number of sequential days to seed infections after
      the 10th death in a country. (N0 in the authors' Stan code.)
    total_days: Integer, number of days of observed data plus days to forecast.
      (N2 in the authors' Stan code.)
  Returns:
    predicted_infections: Array of shape
      `[total_days, batch_size, num_countries]`. (Batched) predicted number of
      infections over time and by country.
  """
  alpha = alpha_hier - tf.cast(np.log(1.05) / 6.0, DTYPE)

  # Multiply the effectiveness of each intervention in each country (alpha)
  # by the indicator variable for whether the intervention was active and sum
  # over interventions, yielding an array of shape
  # [total_days, batch_size, num_countries] that represents the total effectiveness of
  # all interventions in each country on each day (for a batch of data).
  linear_prediction = tf.einsum(
      'ijk,...k->j...i', intervention_indicators, alpha)

  # Adjust the reproduction rate per country downward, according to the
  # effectiveness of the interventions.
  rt = mu * tf.exp(-linear_prediction, name='reproduction_rate')

  # Initialize storage array for daily infections and seed it with initial
  # cases.
  daily_infections = tf.TensorArray(
      dtype=DTYPE, size=total_days, element_shape=initial_cases.shape)
  for i in range(initial_days):
    daily_infections = daily_infections.write(i, initial_cases)

  # Initialize cumulative cases.
  init_cumulative_infections = initial_cases * initial_days

  # Simulate forward for total_days days.
  cond = lambda i, *_: i < total_days
  def body(i, prev_daily_infections, prev_cumulative_infections):
    # The probability distribution over days j that someone infected on day i
    # caught the virus from someone infected on day j.
    p_infected_on_day = tf.gather(
        conv_serial_interval, i - initial_days, axis=0)

    # Multiply p_infected_on_day by the number previous infections each day and
    # by mu, and sum to obtain new infections on day i. Mu is adjusted by
    # the fraction of the population already infected, so that the population
    # size is the upper limit on the number of infections.
    prev_daily_infections_array = prev_daily_infections.stack()
    to_sum = prev_daily_infections_array * bu.left_justified_expand_dims_like(
        p_infected_on_day, prev_daily_infections_array)
    convolution = tf.reduce_sum(to_sum, axis=0)
    rt_adj = (
        (population - prev_cumulative_infections) / population
        ) * tf.gather(rt, i)
    new_infections = rt_adj * convolution

    # Update the prediction array and the cumulative number of infections.
    daily_infections = prev_daily_infections.write(i, new_infections)
    cumulative_infections = prev_cumulative_infections + new_infections
    return i + 1, daily_infections, cumulative_infections

  _, daily_infections_final, last_cumm_sum = tf.while_loop(
      cond, body,
      (initial_days, daily_infections, init_cumulative_infections),
      maximum_iterations=(total_days - initial_days))
  return daily_infections_final.stack()

def predict_deaths(predicted_infections, ifr_noise, conv_fatality_rate):
  """Expected number of reported deaths by country, by day.

  Args:
    predicted_infections: Array of shape
      `[total_days, batch_size, num_countries]` output from
      `predict_infections`.
    ifr_noise: Array of shape `[batch_size, num_countries]`. Noise in Infection
      Fatality Rate (IFR).
    conv_fatality_rate: Array of shape
      `[total_days - 1, total_days, num_countries]`. Convolutional kernel for
      calculating fatalities, output from `make_conv_fatality_rate`.
  Returns:
    predicted_deaths: Array of shape `[total_days, batch_size, num_countries]`.
      (Batched) predicted number of deaths over time and by country.
  """
  # Multiply the number of infections on day j by the probability of death
  # on day i given infection on day j, and sum over j. This yields the expected
  result_remainder = tf.einsum(
      'i...j,kij->k...j', predicted_infections, conv_fatality_rate) * ifr_noise

  # Concatenate the result with a vector of zeros so that the first day is
  # included.
  result_temp = 1e-15 * predicted_infections[:1]
  return tf.concat([result_temp, result_remainder], axis=0)

1.2 Przed wartościami parametrów

Tutaj definiujemy łączny uprzedni rozkład parametrów modelu. Zakłada się, że wiele wartości parametrów jest niezależnych, tak że a priori można wyrazić jako:

\(\text p(\tau, y, \psi, \kappa, \mu, \alpha) = \text p(\tau)\text p(y|\tau)\text p(\psi)\text p(\kappa)\text p(\mu|\kappa)\text p(\alpha)\text p(\epsilon)\)

w którym:

  • \(\tau\) jest parametrem wspólna stawka rozkład wykładniczy nad liczby początkowych przypadków na kraj, \(y = y_1, ... y_{\text{num_countries} }\).
  • \(\psi\) jest parametrem w Rozkład Pascala dla liczby zgonów.
  • \(\kappa\) jest parametrem skali wspólne rozkładu HalfNormal nad początkowej liczby reprodukcji w każdym kraju \(\mu = \mu_1, ..., \mu_{\text{num_countries} }\) (wskazując liczbę dodatkowych przypadków transmitowanych przez każdego zakażoną osobą).
  • \(\alpha = \alpha_1, ..., \alpha_6\) jest skuteczność każdego z sześciu interwencji.
  • \(\epsilon\) (tzw ifr_noise w kodzie, po kodzie Stan autorów) jest hałas w Infection Fatality Rate (IFR).

Wyrażamy ten model jako TFP JointDistribution, rodzaj dystrybucji TFP, który umożliwia wyrażenie probabilistycznych modeli graficznych.

def make_jd_prior(num_countries, num_interventions):
  return tfd.JointDistributionSequentialAutoBatched([
      # Rate parameter for the distribution of initial cases (tau).
      tfd.Exponential(rate=tf.cast(0.03, DTYPE)),

      # Initial cases for each country.
      lambda tau: tfd.Sample(
          tfd.Exponential(rate=tf.cast(1, DTYPE) / tau),
          sample_shape=num_countries),

      # Parameter in Negative Binomial model for deaths (psi).
      tfd.HalfNormal(scale=tf.cast(5, DTYPE)),

      # Parameter in the distribution over the initial reproduction number, R_0
      # (kappa).
      tfd.HalfNormal(scale=tf.cast(0.5, DTYPE)),

      # Initial reproduction number, R_0, for each country (mu).
      lambda kappa: tfd.Sample(
          tfd.TruncatedNormal(loc=3.28, scale=kappa, low=1e-5, high=1e5),
          sample_shape=num_countries),

      # Impact of interventions (alpha; shared for all countries).
      tfd.Sample(
          tfd.Gamma(tf.cast(0.1667, DTYPE), 1), sample_shape=num_interventions),

      # Multiplicative noise in Infection Fatality Rate.
      tfd.Sample(
          tfd.TruncatedNormal(
              loc=tf.cast(1., DTYPE), scale=0.1, low=1e-5, high=1e5),
              sample_shape=num_countries)
  ])

1.3 Prawdopodobieństwo zaobserwowanych zgonów w zależności od wartości parametrów

Modelowe prawdopodobieństwo wyraża \(p(\text{deaths} | \tau, y, \psi, \kappa, \mu, \alpha, \epsilon)\). Stosuje modele dla liczby zakażeń i oczekiwanych zgonów uzależnionych od parametrów i zakłada, że ​​rzeczywiste zgony są zgodne z ujemnym rozkładem dwumianowym.

def make_likelihood_fn(
    intervention_indicators, population, deaths,
    infection_fatality_rate, initial_days, total_days):

  # Create a mask for the initial days of simulated data, as they are not
  # counted in the likelihood.
  observed_deaths = tf.constant(deaths.T[np.newaxis, ...], dtype=DTYPE)
  mask_temp = deaths != -1
  mask_temp[:, :START_DAYS] = False
  observed_deaths_mask = tf.constant(mask_temp.T[np.newaxis, ...])

  conv_serial_interval = make_conv_serial_interval(initial_days, total_days)
  conv_fatality_rate = make_conv_fatality_rate(
      infection_fatality_rate, total_days)

  def likelihood_fn(tau, initial_cases, psi, kappa, mu, alpha_hier, ifr_noise):
    # Run models for infections and expected deaths
    predicted_infections = predict_infections(
        intervention_indicators, population, initial_cases, mu, alpha_hier,
        conv_serial_interval, initial_days, total_days)
    e_deaths_all_countries = predict_deaths(
        predicted_infections, ifr_noise, conv_fatality_rate)

    # Construct the Negative Binomial distribution for deaths by country.
    mu_m = tf.transpose(e_deaths_all_countries, [1, 0, 2])
    psi_m = psi[..., tf.newaxis, tf.newaxis]
    probs = tf.clip_by_value(mu_m / (mu_m + psi_m), 1e-9, 1.)
    likelihood_elementwise = tfd.NegativeBinomial(
        total_count=psi_m, probs=probs).log_prob(observed_deaths)
    return tf.reduce_sum(
        tf.where(observed_deaths_mask,
                likelihood_elementwise,
                tf.zeros_like(likelihood_elementwise)),
        axis=[-2, -1])

  return likelihood_fn

1.4 Prawdopodobieństwo zgonu z powodu infekcji

Ta sekcja oblicza rozkład zgonów w dniach następujących po zakażeniu. Zakłada się, że czas od zakażenia do zgonu jest sumą dwóch zmiennych Gamma, reprezentujących czas od zakażenia do wystąpienia choroby oraz czas od zachorowania do zgonu. Podział czasu do śmierci w połączeniu z zakażeniem Śmiertelność szybkość transmisji danych z Verity et al. (2020) , aby obliczyć prawdopodobieństwo śmierci w dniach po zakażeniu.

def daily_fatality_probability(infection_fatality_rate, total_days):
  """Computes the probability of death `d` days after infection."""

  # Convert from alternative Gamma parametrization and construct distributions
  # for number of days from infection to onset and onset to death.
  concentration1 = tf.cast((1. / 0.86)**2, DTYPE)
  rate1 = concentration1 / 5.1
  concentration2 = tf.cast((1. / 0.45)**2, DTYPE)
  rate2 = concentration2 / 18.8
  infection_to_onset = tfd.Gamma(concentration=concentration1, rate=rate1)
  onset_to_death = tfd.Gamma(concentration=concentration2, rate=rate2)

  # Create empirical distribution for number of days from infection to death.
  inf_to_death_dist = tfd.Empirical(
      infection_to_onset.sample([5e6]) + onset_to_death.sample([5e6]))

  # Subtract the CDF value at day i from the value at day i + 1 to compute the
  # probability of death on day i given infection on day 0, and given that
  # death (not recovery) is the outcome.
  times = np.arange(total_days + 1., dtype=DTYPE) + 0.5
  cdf = inf_to_death_dist.cdf(times).numpy()
  f_before_ifr = cdf[1:] - cdf[:-1]
  # Explicitly set the zeroth value to the empirical cdf at time 1.5, to include
  # the mass between time 0 and time .5.
  f_before_ifr[0] = cdf[1]

  # Multiply the daily fatality rates conditional on infection and eventual
  # death (f_before_ifr) by the infection fatality rates (probability of death
  # given intection) to obtain the probability of death on day i conditional
  # on infection on day 0.
  return infection_fatality_rate[..., np.newaxis] * f_before_ifr

def make_conv_fatality_rate(infection_fatality_rate, total_days):
  """Computes the probability of death on day `i` given infection on day `j`."""
  p_fatal_all_countries = daily_fatality_probability(
      infection_fatality_rate, total_days)

  # Use the probability of death d days after infection in each country
  # to build an array of shape [total_days - 1, total_days, num_countries],
  # where the element [i, j, c] is the probability of death on day i+1 given
  # infection on day j in country c.
  conv_fatality_rate = np.zeros(
      [total_days - 1, total_days, p_fatal_all_countries.shape[0]])
  for n in range(1, total_days):
    conv_fatality_rate[n - 1, 0:n, :] = (
        p_fatal_all_countries[:, n - 1::-1]).T
  return tf.constant(conv_fatality_rate, dtype=DTYPE)

1.5 Interwał szeregowy

Odstęp seryjny to czas między kolejnymi przypadkami w łańcuchu przenoszenia choroby i zakłada się, że ma rozkład gamma. Używamy seryjny rozkład odstępu obliczyć prawdopodobieństwo, że dana osoba zainfekowana na dzień \(i\) złowionych wirusa z zakażonej osoby uprzednio na dzień \(j\) (The conv_serial_interval argumentów do predict_infections ).

def make_conv_serial_interval(initial_days, total_days):
  """Construct the convolutional kernel for infection timing."""

  g = tfd.Gamma(tf.cast(1. / (0.62**2), DTYPE), 1./(6.5*0.62**2))
  g_cdf = g.cdf(np.arange(total_days, dtype=DTYPE))

  # Approximate the probability mass function for the number of days between
  # successive infections.
  serial_interval = g_cdf[1:] - g_cdf[:-1]

  # `conv_serial_interval` is an array of shape
  # [total_days - initial_days, total_days] in which entry [i, j] contains the
  # probability that an individual infected on day i + initial_days caught the
  # virus from someone infected on day j.
  conv_serial_interval = np.zeros([total_days - initial_days, total_days])
  for n in range(initial_days, total_days):
    conv_serial_interval[n - initial_days, 0:n] = serial_interval[n - 1::-1]
  return tf.constant(conv_serial_interval, dtype=DTYPE)

2 Wstępne przetwarzanie danych

COUNTRIES = [
    'Austria',
    'Belgium',
    'Denmark',
    'France',
    'Germany',
    'Italy',
    'Norway',
    'Spain',
    'Sweden',
    'Switzerland',
    'United_Kingdom'
]

2.1 Pobieranie i przetwarzanie danych dotyczących interwencji

2.2 Pobierz dane dotyczące przypadku/śmierci i dołącz do interwencji

2.3 Pobierz i przetwórz wskaźnik śmiertelności zarażonych i dane dotyczące populacji

2.4 Wstępne przetwarzanie danych specyficznych dla kraju

# Model up to 75 days of data for each country, starting 30 days before the
# tenth cumulative death.
START_DAYS = 30
MAX_DAYS = 102
COVARIATE_COLUMNS = any_intervention_list + ['any_intervention']

# Initialize an array for number of deaths.
deaths = -np.ones((num_countries, MAX_DAYS), dtype=DTYPE)

# Assuming every intervention is still inplace in the unobserved future
num_interventions = len(COVARIATE_COLUMNS)
intervention_indicators = np.ones((num_countries, MAX_DAYS, num_interventions))

first_days = {}
for i, c in enumerate(COUNTRIES):
  c_data = data.loc[c]

  # Include data only after 10th death in a country.
  mask = c_data['deaths'].cumsum() >= 10

  # Get the date that the epidemic starts in a country.
  first_day = c_data.index[mask][0] - pd.to_timedelta(START_DAYS, 'days')
  c_data = c_data.truncate(before=first_day)

  # Truncate the data after 28 March 2020 for comparison with Flaxman et al.
  c_data = c_data.truncate(after='2020-03-28')

  c_data = c_data.iloc[:MAX_DAYS]
  days_of_data = c_data.shape[0]
  deaths[i, :days_of_data] = c_data['deaths']
  intervention_indicators[i, :days_of_data] = c_data[
    COVARIATE_COLUMNS].to_numpy()
  first_days[c] = first_day

# Number of sequential days to seed infections after the 10th death in a
# country. (N0 in authors' Stan code.)
INITIAL_DAYS = 6

# Number of days of observed data plus days to forecast. (N2 in authors' Stan
# code.)
TOTAL_DAYS = deaths.shape[1]

3 Wnioskowanie o modelu

Flaxman i in. (2020) używane Stan na próbki z tylnej parametru z Hamiltona Monte Carlo (HMC) i No-U-Turn Sampler (NUTS).

Tutaj stosujemy HMC z podwójnym uśrednianiem adaptacji wielkości kroku. Używamy pilotażowego uruchomienia konsoli HMC do wstępnego uwarunkowania i inicjalizacji.

Wnioskowanie działa w ciągu kilku minut na GPU.

3.1 Zbuduj wcześniejsze i prawdopodobieństwo dla modelu

jd_prior = make_jd_prior(num_countries, num_interventions)
likelihood_fn = make_likelihood_fn(
    intervention_indicators, population_value, deaths,
    infection_fatality_rate, INITIAL_DAYS, TOTAL_DAYS)

3.2 Narzędzia

def get_bijectors_from_samples(samples, unconstraining_bijectors, batch_axes):
  """Fit bijectors to the samples of a distribution.

  This fits a diagonal covariance multivariate Gaussian transformed by the
  `unconstraining_bijectors` to the provided samples. The resultant
  transformation can be used to precondition MCMC and other inference methods.
  """
  state_std = [    
      tf.math.reduce_std(bij.inverse(x), axis=batch_axes)
      for x, bij in zip(samples, unconstraining_bijectors)
  ]
  state_mu = [
      tf.math.reduce_mean(bij.inverse(x), axis=batch_axes)
      for x, bij in zip(samples, unconstraining_bijectors)
  ]
  return [tfb.Chain([cb, tfb.Shift(sh), tfb.Scale(sc)])
          for cb, sh, sc in zip(unconstraining_bijectors, state_mu, state_std)]

def generate_init_state_and_bijectors_from_prior(nchain, unconstraining_bijectors):
  """Creates an initial MCMC state, and bijectors from the prior."""
  prior_samples = jd_prior.sample(4096)

  bijectors = get_bijectors_from_samples(
      prior_samples, unconstraining_bijectors, batch_axes=0)

  init_state = [
    bij(tf.zeros([nchain] + list(s), DTYPE))
    for s, bij in zip(jd_prior.event_shape, bijectors)
  ]

  return init_state, bijectors

@tf.function(autograph=False, experimental_compile=True)
def sample_hmc(
    init_state,
    step_size,
    target_log_prob_fn,
    unconstraining_bijectors,
    num_steps=500,
    burnin=50,
    num_leapfrog_steps=10):

    def trace_fn(_, pkr):
        return {
            'target_log_prob': pkr.inner_results.inner_results.accepted_results.target_log_prob,
            'diverging': ~(pkr.inner_results.inner_results.log_accept_ratio > -1000.),
            'is_accepted': pkr.inner_results.inner_results.is_accepted,
            'step_size': [tf.exp(s) for s in pkr.log_averaging_step],
        }

    hmc = tfp.mcmc.HamiltonianMonteCarlo(
        target_log_prob_fn,
        step_size=step_size,
        num_leapfrog_steps=num_leapfrog_steps)

    hmc = tfp.mcmc.TransformedTransitionKernel(
        inner_kernel=hmc,
        bijector=unconstraining_bijectors)

    hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
        hmc,
        num_adaptation_steps=int(burnin * 0.8),
        target_accept_prob=0.8,
        decay_rate=0.5)

    # Sampling from the chain.
    return tfp.mcmc.sample_chain(
        num_results=burnin + num_steps,
        current_state=init_state,
        kernel=hmc,
        trace_fn=trace_fn)

3.3 Definiowanie bijektorów przestrzeni zdarzeń

HMC jest najbardziej wydajny podczas pobierania próbek z izotropowym wieloczynnikowej rozkładu Gaussa ( Mangoubi & Smith (2017) ), więc pierwszym krokiem jest warunkować gęstość docelową wyglądać tak samo jak to, jak to możliwe.

Przede wszystkim przekształcamy ograniczone (np. nieujemne) zmienne w nieograniczoną przestrzeń, której wymaga HMC. Dodatkowo używamy bijectora SinhArcsinh do manipulowania ciężkością ogonów przekształconej gęstości docelowej; Chcemy, aby te odpaść z grubsza jako \(e^{-x^2}\).

unconstraining_bijectors = [
    tfb.Chain([tfb.Scale(tf.constant(1 / 0.03, DTYPE)), tfb.Softplus(),
                tfb.SinhArcsinh(tailweight=tf.constant(1.85, DTYPE))]), # tau
    tfb.Chain([tfb.Scale(tf.constant(1 / 0.03, DTYPE)), tfb.Softplus(),
                tfb.SinhArcsinh(tailweight=tf.constant(1.85, DTYPE))]), # initial_cases
    tfb.Softplus(), # psi
    tfb.Softplus(), # kappa
    tfb.Softplus(), # mu
    tfb.Chain([tfb.Scale(tf.constant(0.4, DTYPE)), tfb.Softplus(),
                tfb.SinhArcsinh(skewness=tf.constant(-0.2, DTYPE), tailweight=tf.constant(2., DTYPE))]), # alpha
    tfb.Softplus(), # ifr_noise
]

3.4 Pilotaż konsoli HMC

Najpierw uruchamiamy HMC wstępnie uwarunkowane przez poprzednie, zainicjowane od zer w przekształconej przestrzeni. Nie używamy poprzednich próbek do inicjalizacji łańcucha, ponieważ w praktyce często powodują one zacinanie się łańcuchów z powodu słabej wartości liczbowej.

%%time

nchain = 32

target_log_prob_fn = lambda *x: jd_prior.log_prob(*x) + likelihood_fn(*x)
init_state, bijectors = generate_init_state_and_bijectors_from_prior(nchain, unconstraining_bijectors)

# Each chain gets its own step size.
step_size = [tf.fill([nchain] + [1] * (len(s.shape) - 1), tf.constant(0.01, DTYPE)) for s in init_state]

burnin = 200
num_steps = 100

pilot_samples, pilot_sampler_stat = sample_hmc(
    init_state,
    step_size,
    target_log_prob_fn,
    bijectors,
    num_steps=num_steps,
    burnin=burnin,
    num_leapfrog_steps=10)

CPU times: user 56.8 s, sys: 2.34 s, total: 59.1 s
Wall time: 1min 1s

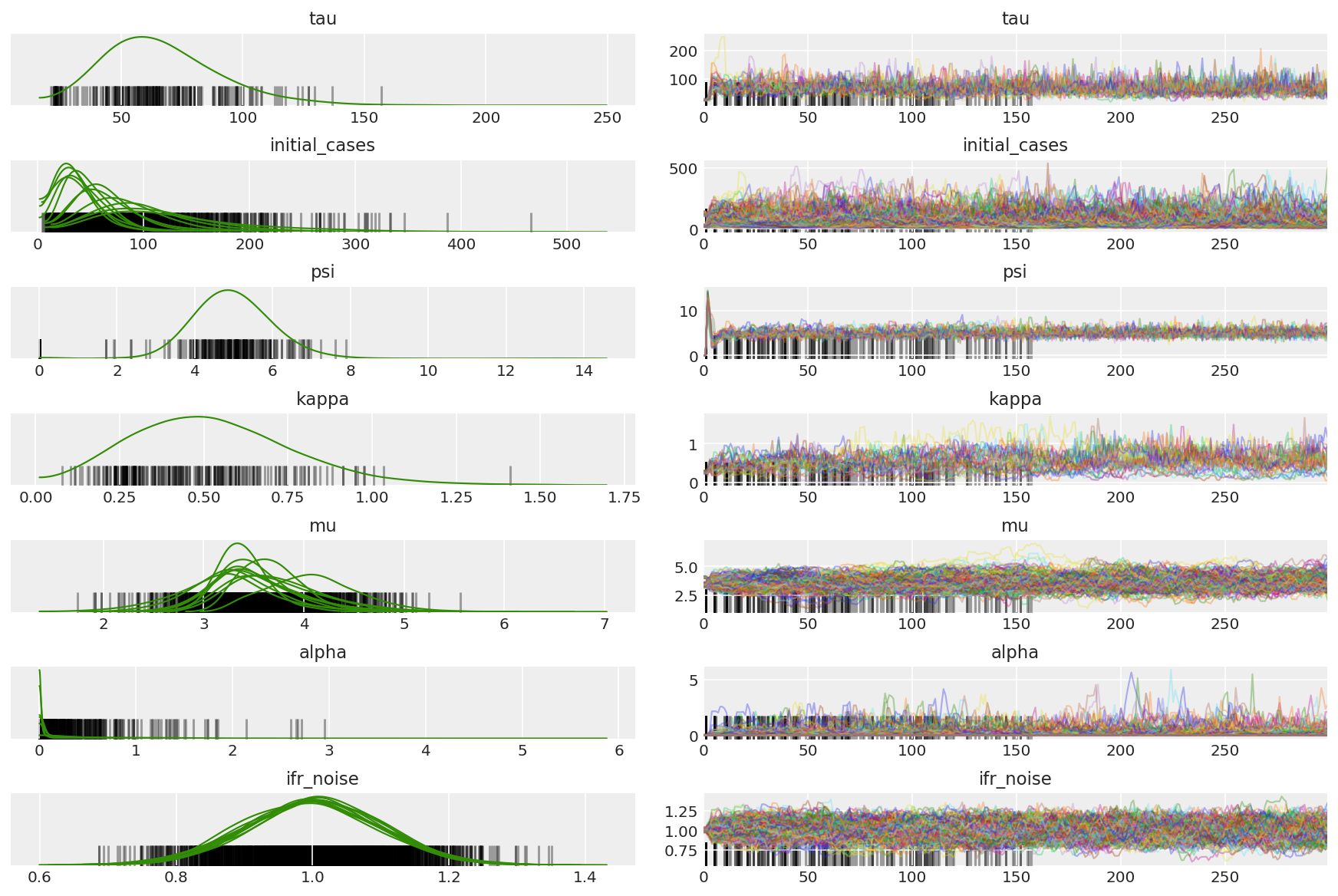
3.5 Wizualizuj próbki pilotażowe

Szukamy zablokowanych łańcuchów i przykuwającej wzrok konwergencji. Możemy tutaj przeprowadzić formalną diagnostykę, ale nie jest to konieczne, biorąc pod uwagę, że to tylko uruchomienie pilotażowe.

import arviz as az
az.style.use('arviz-darkgrid')

var_name = ['tau', 'initial_cases', 'psi', 'kappa', 'mu', 'alpha', 'ifr_noise']

pilot_with_warmup = {k: np.swapaxes(v.numpy(), 1, 0)
                     for k, v in zip(var_name, pilot_samples)}

Obserwujemy rozbieżności podczas rozgrzewki, głównie dlatego, że adaptacja podwójnego uśredniania rozmiaru kroku wykorzystuje bardzo agresywne wyszukiwanie optymalnego rozmiaru kroku. Gdy adaptacja się wyłączy, znikają również rozbieżności.

az_trace = az.from_dict(posterior=pilot_with_warmup,
                        sample_stats={'diverging': np.swapaxes(pilot_sampler_stat['diverging'].numpy(), 0, 1)})
az.plot_trace(az_trace, combined=True, compact=True, figsize=(12, 8));

png

plt.plot(pilot_sampler_stat['step_size'][0]);

png

3.6 Uruchom konsolę HMC

W zasadzie moglibyśmy użyć próbek pilotażowych do analizy końcowej (jeśli uruchomimy ją dłużej, aby uzyskać zbieżność), ale nieco bardziej wydajne jest rozpoczęcie kolejnego uruchomienia HMC, tym razem wstępnie przygotowanego i zainicjowanego przez próbki pilotażowe.

%%time

burnin = 50
num_steps = 200

bijectors = get_bijectors_from_samples([s[burnin:] for s in pilot_samples],
                                       unconstraining_bijectors=unconstraining_bijectors,
                                       batch_axes=(0, 1))

samples, sampler_stat = sample_hmc(
    [s[-1] for s in pilot_samples],
    [s[-1] for s in pilot_sampler_stat['step_size']],
    target_log_prob_fn,
    bijectors,
    num_steps=num_steps,
    burnin=burnin,
    num_leapfrog_steps=20)

CPU times: user 1min 26s, sys: 3.88 s, total: 1min 30s
Wall time: 1min 32s

plt.plot(sampler_stat['step_size'][0]);

png

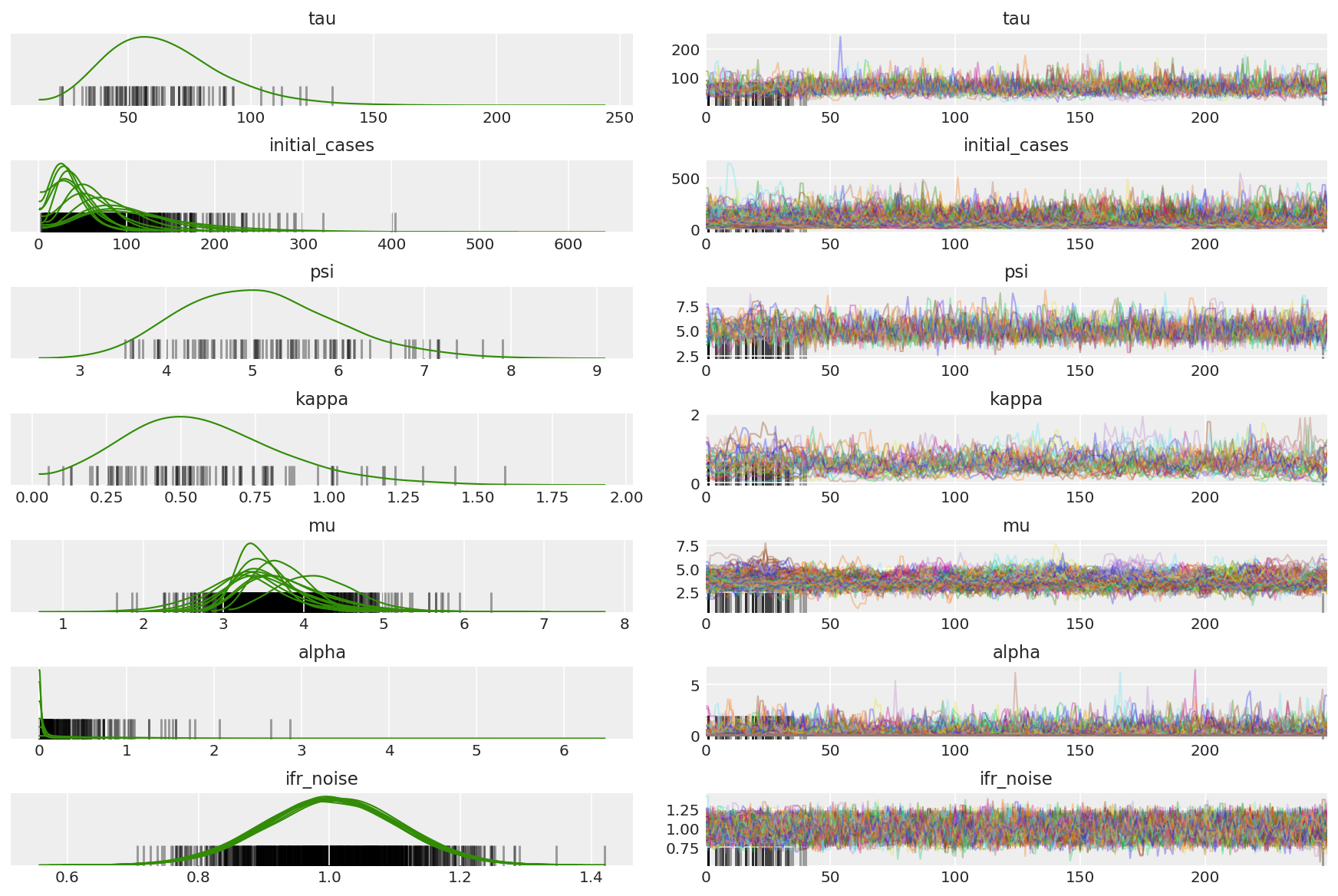
3.7 Wizualizuj próbki

import arviz as az
az.style.use('arviz-darkgrid')

var_name = ['tau', 'initial_cases', 'psi', 'kappa', 'mu', 'alpha', 'ifr_noise']

posterior = {k: np.swapaxes(v.numpy()[burnin:], 1, 0)
             for k, v in zip(var_name, samples)}
posterior_with_warmup = {k: np.swapaxes(v.numpy(), 1, 0)
             for k, v in zip(var_name, samples)}

Oblicz podsumowanie łańcuchów. Szukamy wysokiego ESS i r_hat bliskiego 1.

az.summary(posterior)

az_trace = az.from_dict(posterior=posterior_with_warmup,
                        sample_stats={'diverging': np.swapaxes(sampler_stat['diverging'].numpy(), 0, 1)})
az.plot_trace(az_trace, combined=True, compact=True, figsize=(12, 8));

png

Pouczające jest przyjrzenie się funkcjom autokorelacji we wszystkich wymiarach. Szukamy funkcji, które szybko się obniżają, ale nie tak bardzo, aby przeszły w ujemną wartość (co wskazuje, że HMC uderza w rezonans, co jest niekorzystne dla ergodyczności i może wprowadzać błąd).

with az.rc_context(rc={'plot.max_subplots': None}):
  az.plot_autocorr(posterior, combined=True, figsize=(12, 16), textsize=12);

png

4 Wyniki

Poniższe wykresy analizy predykcyjne rozkład tylnej ponad \(R_t\), liczba zgonów i liczby infekcji, podobnie do analizy w Flaxman et al. (2020).

total_num_samples = np.prod(posterior['mu'].shape[:2])

# Calculate R_t given parameter estimates.
def rt_samples_batched(mu, intervention_indicators, alpha):
  linear_prediction = tf.reduce_sum(
      intervention_indicators * alpha[..., np.newaxis, np.newaxis, :], axis=-1)
  rt_hat = mu[..., tf.newaxis] * tf.exp(-linear_prediction, name='rt')
  return rt_hat

alpha_hat = tf.convert_to_tensor(
    posterior['alpha'].reshape(total_num_samples, posterior['alpha'].shape[-1]))
mu_hat = tf.convert_to_tensor(
    posterior['mu'].reshape(total_num_samples, num_countries))
rt_hat = rt_samples_batched(mu_hat, intervention_indicators, alpha_hat)
sampled_initial_cases = posterior['initial_cases'].reshape(
    total_num_samples, num_countries)
sampled_ifr_noise = posterior['ifr_noise'].reshape(
    total_num_samples, num_countries)
psi_hat = posterior['psi'].reshape([total_num_samples])

conv_serial_interval = make_conv_serial_interval(INITIAL_DAYS, TOTAL_DAYS)
conv_fatality_rate = make_conv_fatality_rate(infection_fatality_rate, TOTAL_DAYS)
pred_hat = predict_infections(
    intervention_indicators, population_value, sampled_initial_cases, mu_hat,
    alpha_hat, conv_serial_interval, INITIAL_DAYS, TOTAL_DAYS)
expected_deaths = predict_deaths(pred_hat, sampled_ifr_noise, conv_fatality_rate)

psi_m = psi_hat[np.newaxis, ..., np.newaxis]
probs = tf.clip_by_value(expected_deaths / (expected_deaths + psi_m), 1e-9, 1.)
predicted_deaths = tfd.NegativeBinomial(
    total_count=psi_m, probs=probs).sample()

# Predict counterfactual infections/deaths in the absence of interventions
no_intervention_infections = predict_infections(
    intervention_indicators,
    population_value,
    sampled_initial_cases,
    mu_hat,
    tf.zeros_like(alpha_hat),
    conv_serial_interval,
    INITIAL_DAYS, TOTAL_DAYS)

no_intervention_expected_deaths = predict_deaths(
    no_intervention_infections, sampled_ifr_noise, conv_fatality_rate)
probs = tf.clip_by_value(
    no_intervention_expected_deaths / (no_intervention_expected_deaths + psi_m),
    1e-9, 1.)
no_intervention_predicted_deaths = tfd.NegativeBinomial(
    total_count=psi_m, probs=probs).sample()

4.1 Skuteczność interwencji

Podobnie jak na rycinie 4 Flaxman et al. (2020).

def intervention_effectiveness(alpha):

  alpha_adj = 1. - np.exp(-alpha + np.log(1.05) / 6.)
  alpha_adj_first = (
      1. - np.exp(-alpha - alpha[..., -1:] + np.log(1.05) / 6.))

  fig, ax = plt.subplots(1, 1, figsize=[12, 6])
  intervention_perm = [2, 1, 3, 4, 0]
  percentile_vals = [2.5, 97.5]
  jitter = .2

  for ind in range(5):
    first_low, first_high = tfp.stats.percentile(
        alpha_adj_first[..., ind], percentile_vals)
    low, high = tfp.stats.percentile(
        alpha_adj[..., ind], percentile_vals)

    p_ind = intervention_perm[ind]
    ax.hlines(p_ind, low, high, label='Later Intervention', colors='g')
    ax.scatter(alpha_adj[..., ind].mean(), p_ind, color='g')
    ax.hlines(p_ind + jitter, first_low, first_high,
              label='First Intervention', colors='r')
    ax.scatter(alpha_adj_first[..., ind].mean(), p_ind + jitter, color='r')

    if ind == 0:
      plt.legend(loc='lower right')
  ax.set_yticks(range(5))
  ax.set_yticklabels(
      [any_intervention_list[intervention_perm.index(p)] for p in range(5)])
  ax.set_xlim([-0.01, 1.])
  r = fig.patch
  r.set_facecolor('white') 

intervention_effectiveness(alpha_hat)

png

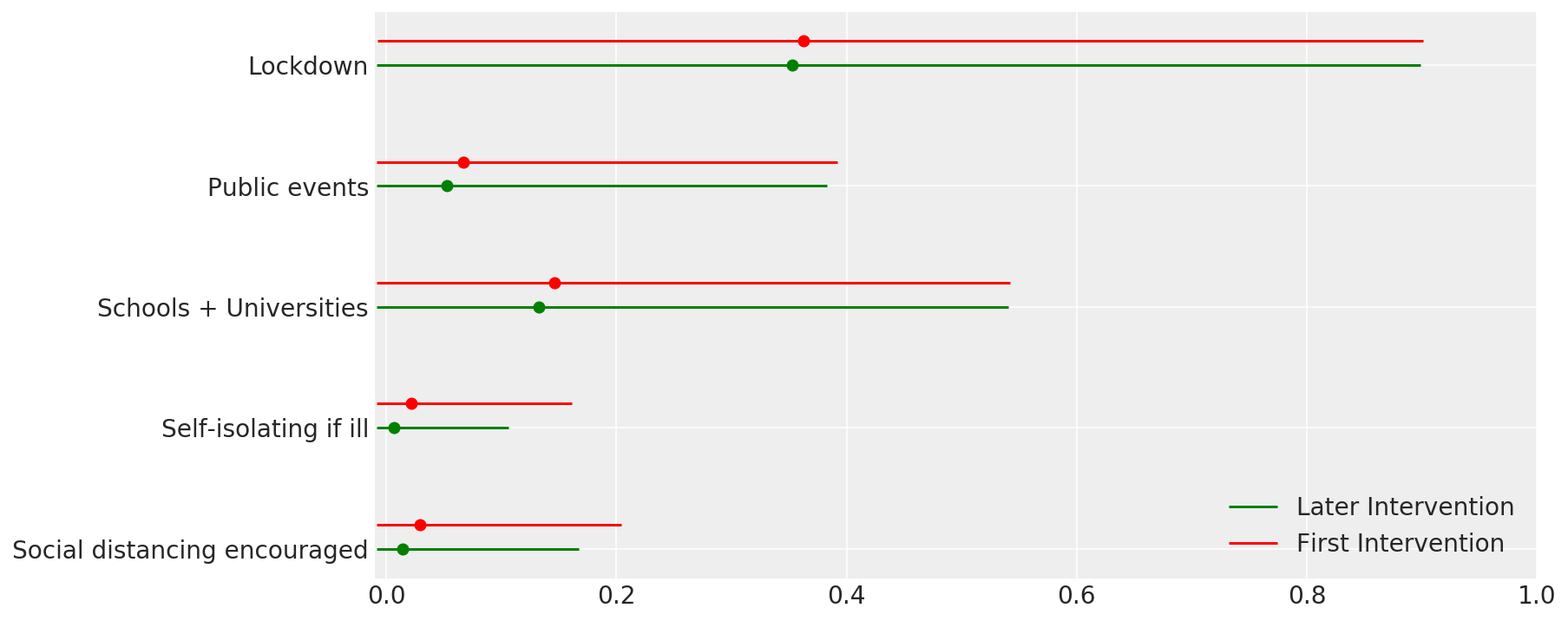
4.2 Zakażenia, zgony i R_t według kraju

Podobnie jak na rycinie 2 Flaxman et al. (2020).

png

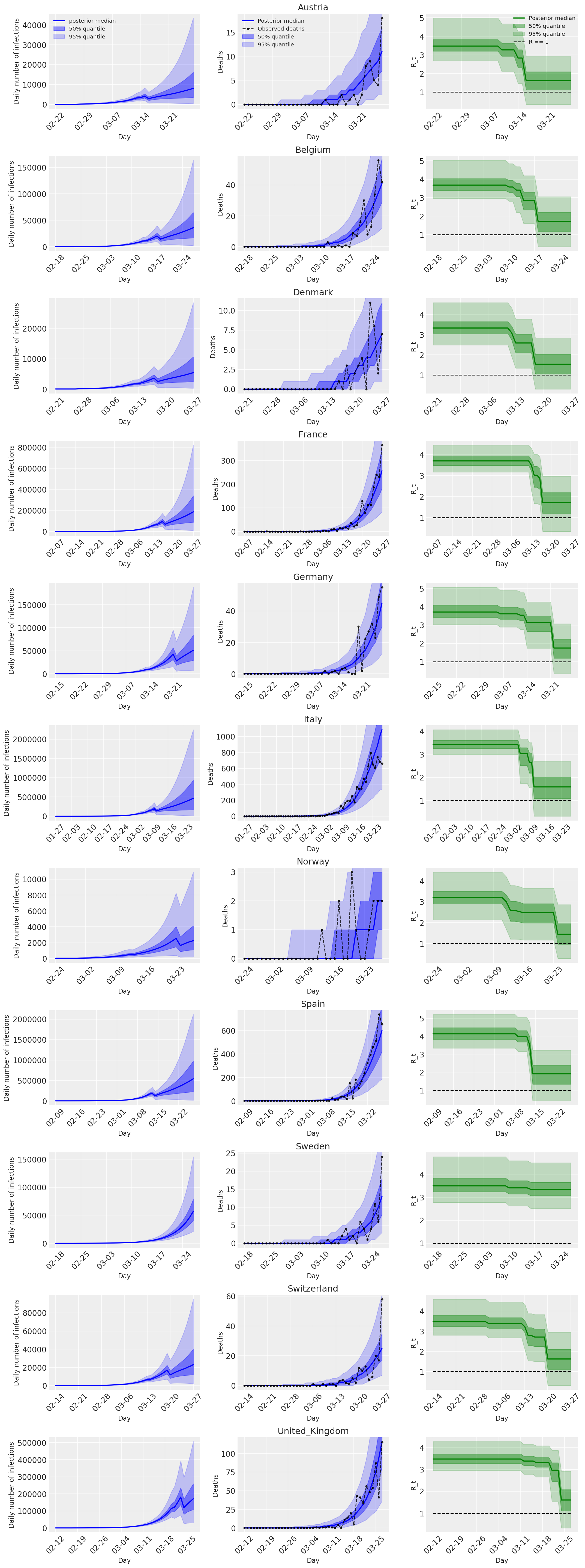
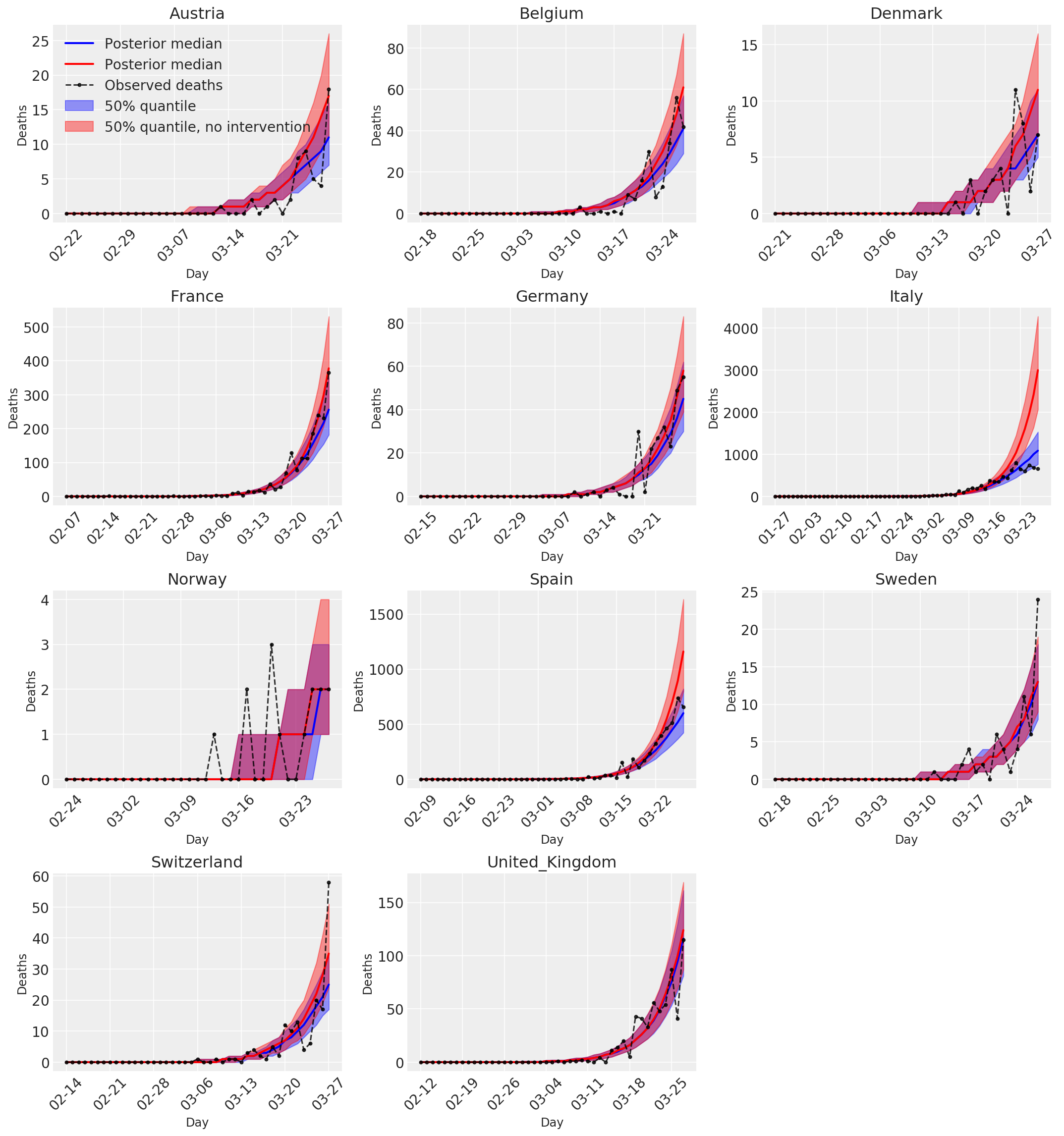
4.3 Dzienna liczba przewidywanych/prognozowanych zgonów z interwencjami i bez interwencji

png