 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
A [copule] (https://en.wikipedia.org/wiki/Copula_ (probability_theory% 29) est une approche classique pour capturer la dépendance entre les variables aléatoires. Plus formellement, une copule est une distribution à plusieurs variables \(C(U_1, U_2, ...., U_n)\) telle que marginalisant donne \(U_i \sim \text{Uniform}(0, 1)\).
Les copules sont intéressantes car nous pouvons les utiliser pour créer des distributions multivariées avec des marginales arbitraires. Voici la recette :
- Utilisation de la probabilité transformée intégrale à tour de rôle un VR continu arbitraire \(X\) en uniforme une \(F_X(X)\), où \(F_X\) est le CDF de \(X\).
- Étant donné copule ( par exemple bivarié) \(C(U, V)\), nous avons que \(U\) et \(V\) ont uniformes distributions marginales.
- Maintenant , étant donné notre RV est d'intérêt \(X, Y\), créer une nouvelle distribution \(C'(X, Y) = C(F_X(X), F_Y(Y))\). Les pour marginaux \(X\) et \(Y\) sont ceux que nous désirions.
Les marginaux sont univariés et peuvent donc être plus faciles à mesurer et/ou modéliser. Une copule permet de partir des marginaux tout en réalisant une corrélation arbitraire entre les dimensions.
Copule Gaussienne
Pour illustrer comment les copules sont construites, considérons le cas de la capture de la dépendance selon des corrélations gaussiennes multivariées. A gaussienne copule est donnée par une \(C(u_1, u_2, ...u_n) = \Phi_\Sigma(\Phi^{-1}(u_1), \Phi^{-1}(u_2), ... \Phi^{-1}(u_n))\) où \(\Phi_\Sigma\) représente la CDF d'un MultivariateNormal, avec covariance \(\Sigma\) et une moyenne de 0 et \(\Phi^{-1}\) est le CDF inverse pour le standard normal.
L'application du CDF inverse de la normale déforme les dimensions uniformes pour qu'elles soient normalement distribuées. L'application du CDF de la normale multivariée écrase ensuite la distribution pour qu'elle soit marginalement uniforme et avec des corrélations gaussiennes.
Ainsi, ce que nous obtenons est que la copule gaussienne est une distribution sur l'unité hypercube \([0, 1]^n\) avec uniformes marginaux.
Défini en tant que tel, la copule gaussienne peut être mis en œuvre avec tfd.TransformedDistribution et approprié Bijector . Autrement dit, nous transformons un MultivariateNormal, via l'utilisation de la distribution normale de CDF inverse, mis en œuvre par le tfb.NormalCDF bijector.
Ci - dessous, nous mettons en œuvre une copule gaussienne avec une hypothèse simplificatrice: que la covariance est paramétré par un facteur de Cholesky (donc une covariance pour MultivariateNormalTriL ). (On pourrait utiliser d' autres tf.linalg.LinearOperators pour coder différentes hypothèses sans matrice.).
class GaussianCopulaTriL(tfd.TransformedDistribution):
"""Takes a location, and lower triangular matrix for the Cholesky factor."""
def __init__(self, loc, scale_tril):
super(GaussianCopulaTriL, self).__init__(
distribution=tfd.MultivariateNormalTriL(
loc=loc,
scale_tril=scale_tril),
bijector=tfb.NormalCDF(),
validate_args=False,
name="GaussianCopulaTriLUniform")
# Plot an example of this.
unit_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(unit_interval, unit_interval)
coordinates = np.concatenate(
[x_grid[..., np.newaxis],
y_grid[..., np.newaxis]], axis=-1)
pdf = GaussianCopulaTriL(
loc=[0., 0.],
scale_tril=[[1., 0.8], [0., 0.6]],
).prob(coordinates)
# Plot its density.
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
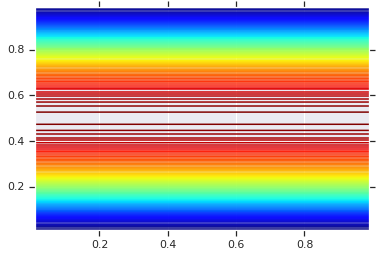
Cependant, la puissance d'un tel modèle utilise la transformation intégrale de probabilité, pour utiliser la copule sur des VR arbitraires. De cette manière, nous pouvons spécifier des marginales arbitraires et utiliser la copule pour les assembler.
On part d'un modèle :
\[\begin{align*} X &\sim \text{Kumaraswamy}(a, b) \\ Y &\sim \text{Gumbel}(\mu, \beta) \end{align*}\]
et utiliser la copule pour obtenir un RV bivarié \(Z\), qui a marginaux Kumaraswamy et Gumbel .
Nous allons commencer par tracer la distribution des produits générés par ces deux véhicules récréatifs. C'est juste pour servir de point de comparaison au moment où nous appliquons la copule.
a = 2.0
b = 2.0
gloc = 0.
gscale = 1.
x = tfd.Kumaraswamy(a, b)
y = tfd.Gumbel(loc=gloc, scale=gscale)
# Plot the distributions, assuming independence
x_axis_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
y_axis_interval = np.linspace(-2., 3., num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(x_axis_interval, y_axis_interval)
pdf = x.prob(x_grid) * y.prob(y_grid)
# Plot its density
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
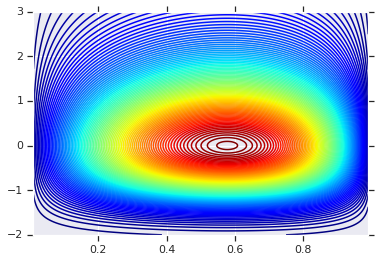
Répartition conjointe avec différents marginaux
Maintenant, nous utilisons une copule gaussienne pour coupler les distributions ensemble et tracer cela. Encore une fois notre outil de choix est TransformedDistribution applique la appropriée Bijector pour obtenir les choisis marginaux.
Plus précisément, nous utilisons un par Blockwise bijector qui applique différents bijectors à différentes parties du vecteur (qui est encore une transformation bijective).
Maintenant, nous pouvons définir la copule que nous voulons. Étant donné une liste de marginales cibles (codées en tant que bijecteurs), nous pouvons facilement construire une nouvelle distribution qui utilise la copule et a les marginales spécifiées.
class WarpedGaussianCopula(tfd.TransformedDistribution):
"""Application of a Gaussian Copula on a list of target marginals.
This implements an application of a Gaussian Copula. Given [x_0, ... x_n]
which are distributed marginally (with CDF) [F_0, ... F_n],
`GaussianCopula` represents an application of the Copula, such that the
resulting multivariate distribution has the above specified marginals.
The marginals are specified by `marginal_bijectors`: These are
bijectors whose `inverse` encodes the CDF and `forward` the inverse CDF.
block_sizes is a 1-D Tensor to determine splits for `marginal_bijectors`
length should be same as length of `marginal_bijectors`.
See tfb.Blockwise for details
"""
def __init__(self, loc, scale_tril, marginal_bijectors, block_sizes=None):
super(WarpedGaussianCopula, self).__init__(
distribution=GaussianCopulaTriL(loc=loc, scale_tril=scale_tril),
bijector=tfb.Blockwise(bijectors=marginal_bijectors,
block_sizes=block_sizes),
validate_args=False,
name="GaussianCopula")
Enfin, utilisons réellement cette copule gaussienne. Nous allons utiliser un Cholesky de \(\begin{bmatrix}1 & 0\\\rho & \sqrt{(1-\rho^2)}\end{bmatrix}\), qui correspondent aux écarts 1, et la corrélation \(\rho\) pour la normale à plusieurs variables.
Nous allons examiner quelques cas :
# Create our coordinates:
coordinates = np.concatenate(
[x_grid[..., np.newaxis], y_grid[..., np.newaxis]], -1)
def create_gaussian_copula(correlation):
# Use Gaussian Copula to add dependence.
return WarpedGaussianCopula(
loc=[0., 0.],
scale_tril=[[1., 0.], [correlation, tf.sqrt(1. - correlation ** 2)]],
# These encode the marginals we want. In this case we want X_0 has
# Kumaraswamy marginal, and X_1 has Gumbel marginal.
marginal_bijectors=[
tfb.Invert(tfb.KumaraswamyCDF(a, b)),
tfb.Invert(tfb.GumbelCDF(loc=0., scale=1.))])
# Note that the zero case will correspond to independent marginals!
correlations = [0., -0.8, 0.8]
copulas = []
probs = []
for correlation in correlations:
copula = create_gaussian_copula(correlation)
copulas.append(copula)
probs.append(copula.prob(coordinates))
# Plot it's density
for correlation, copula_prob in zip(correlations, probs):
plt.figure()
plt.contour(x_grid, y_grid, copula_prob, 100, cmap=plt.cm.jet)
plt.title('Correlation {}'.format(correlation))
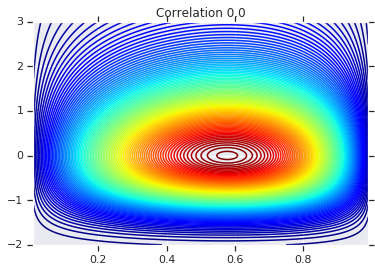
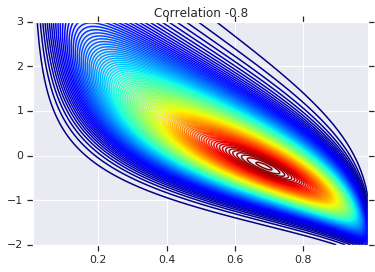
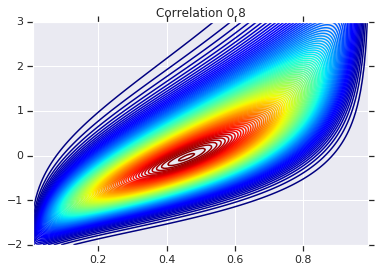
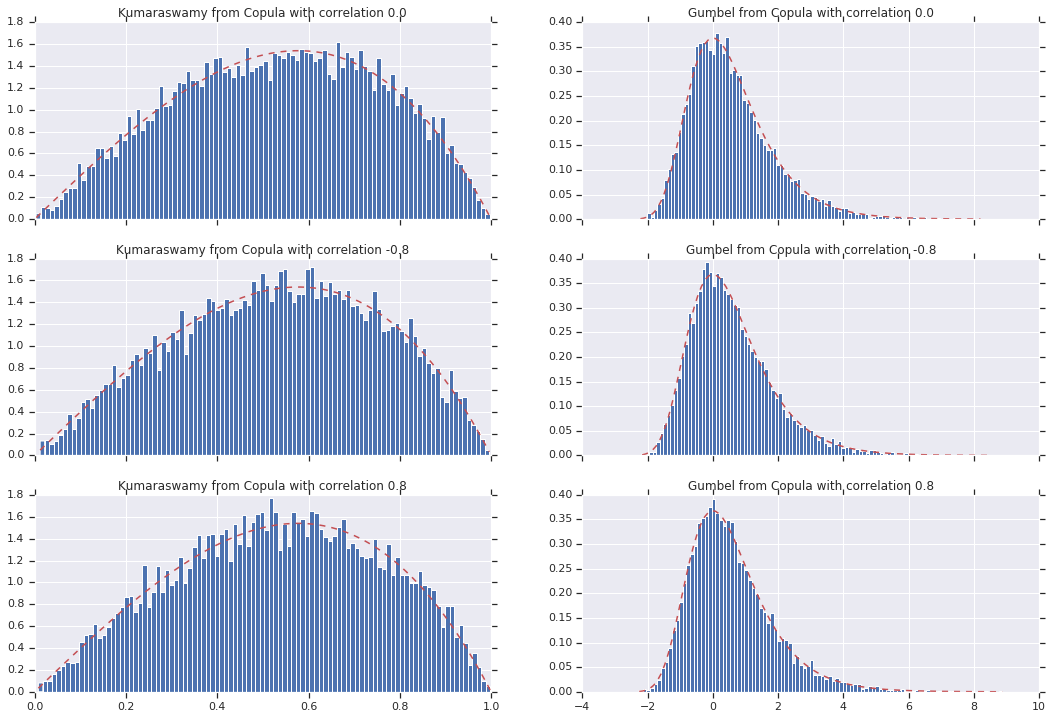
Enfin, vérifions que nous obtenons bien les marginaux que nous voulons.
def kumaraswamy_pdf(x):
return tfd.Kumaraswamy(a, b).prob(np.float32(x))
def gumbel_pdf(x):
return tfd.Gumbel(gloc, gscale).prob(np.float32(x))
copula_samples = []
for copula in copulas:
copula_samples.append(copula.sample(10000))
plot_rows = len(correlations)
plot_cols = 2 # for 2 densities [kumarswamy, gumbel]
fig, axes = plt.subplots(plot_rows, plot_cols, sharex='col', figsize=(18,12))
# Let's marginalize out on each, and plot the samples.
for i, (correlation, copula_sample) in enumerate(zip(correlations, copula_samples)):
k = copula_sample[..., 0].numpy()
g = copula_sample[..., 1].numpy()
_, bins, _ = axes[i, 0].hist(k, bins=100, density=True)
axes[i, 0].plot(bins, kumaraswamy_pdf(bins), 'r--')
axes[i, 0].set_title('Kumaraswamy from Copula with correlation {}'.format(correlation))
_, bins, _ = axes[i, 1].hist(g, bins=100, density=True)
axes[i, 1].plot(bins, gumbel_pdf(bins), 'r--')
axes[i, 1].set_title('Gumbel from Copula with correlation {}'.format(correlation))
Conclusion
Et c'est parti ! Nous avons démontré que nous pouvons construire Copules gaussienne en utilisant l' Bijector API.
De manière plus générale, l' écriture bijectors en utilisant l' Bijector API et qui les composent avec une distribution, peuvent créer des familles riches de distributions pour la modélisation flexible.
