 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Les modèles à variables latentes tentent de capturer la structure cachée dans les données de grande dimension. Les exemples incluent l'analyse en composantes principales (ACP) et l'analyse factorielle. Les processus gaussiens sont des modèles « non paramétriques » qui peuvent capturer de manière flexible la structure de corrélation locale et l'incertitude. Le processus gaussien modèle variable latente ( Lawrence, 2004 ) combine ces concepts.
Contexte : processus gaussiens
Un processus gaussien est toute collection de variables aléatoires telles que la distribution marginale sur tout sous-ensemble fini est une distribution normale multivariée. Pour un aperçu détaillé des médecins généralistes dans le contexte de régression, consultez processus de régression gaussienne dans tensorflow Probabilité .
Nous utilisons un ensemble d'indices que l' on appelle à étiqueter chacune des variables aléatoires dans la collection comprend les GP. Dans le cas d'un ensemble d'indices finis, nous obtenons juste une normale multivariée. GP de sont les plus intéressants, bien que, lorsque l' on considère les collections infinies. Dans le cas des ensembles d'indices comme \(\mathbb{R}^D\), où nous avons une variable aléatoire pour chaque point dans \(D\)espace de dimension, le médecin généraliste peut être considéré comme une distribution sur des fonctions aléatoires. Un seul tirage d'un tel GP, si elle pouvait être réalisée, assignerait un (conjointement normalement distribué) valeur à chaque point \(\mathbb{R}^D\). Dans ce colab, nous allons nous concentrer sur ce GP sur certains\(\mathbb{R}^D\).
Les distributions normales sont complètement déterminées par leurs statistiques de premier et de second ordre -- en effet, une façon de définir la distribution normale est celle dont les cumulants d'ordre supérieur sont tous nuls. Tel est le cas pour les médecins généralistes, aussi: nous précisons complètement un GP en décrivant la * moyenne et covariance. Rappelons que pour les normales multivariées de dimension finie, la moyenne est un vecteur et la covariance est une matrice carrée symétrique définie positive. Dans le GP de dimension infinie, ces structures généralisent à une fonction moyenne \(m : \mathbb{R}^D \to \mathbb{R}\), défini à chaque point de l'ensemble d'indices, et une covariance fonction « noyau »,\(k : \mathbb{R}^D \times \mathbb{R}^D \to \mathbb{R}\). La fonction du noyau doit être définie positive , qui dit en substance que, limitée à un ensemble fini de points, il donne une matrice postiive-définie.
La plupart de la structure d'un GP dérive de sa fonction de noyau de covariance -- cette fonction décrit comment les valeurs des fonctions d'échantillonnage varient à travers des points proches (ou pas si proches). Différentes fonctions de covariance encouragent différents degrés de régularité. Une fonction couramment utilisée du noyau est le « quadratique exponentiation » (alias « gaussienne », « carré exponentielle » ou « fonction de base radiale »), \(k(x, x') = \sigma^2 e^{(x - x^2) / \lambda^2}\). D' autres exemples sont décrits sur David Duvenaud page de livre de cuisine du noyau , ainsi que dans le texte canonique Processus Gauss pour l' apprentissage machine .
* Avec un jeu d'index infini, nous avons également besoin d'une condition de cohérence. Puisque la définition du GP est en termes de marginaux finis, nous devons exiger que ces marginaux soient cohérents quel que soit l'ordre dans lequel les marginaux sont pris. Il s'agit d'un sujet quelque peu avancé dans la théorie des processus stochastiques, hors de portée de ce tutoriel ; il suffit de dire que les choses se passent bien à la fin !
Application des GP : modèles de régression et de variables latentes
Une façon nous pouvons utiliser les médecins généralistes est de la régression: étant donné un tas de données observées sous la forme d'entrées \(\{x_i\}_{i=1}^N\) (éléments de l'ensemble d'indices) et observations\(\{y_i\}_{i=1}^N\), nous pouvons les utiliser pour former une distribution prédictive a posteriori à une nouvelle ensemble de points \(\{x_j^*\}_{j=1}^M\). Étant donné que les distributions sont gaussiennes, cela se résume à une algèbre linéaire simple (mais note: les calculs nécessaires ont l' exécution cube du nombre de points de données et nécessitent quadratique de l' espace dans le nombre de points de données - c'est un facteur limitant majeur l'utilisation de généralistes et de nombreuses recherches actuelles se concentrent sur des alternatives informatiquement viables à l'inférence postérieure exacte). Nous couvrons la régression GP plus en détail dans la régression GP dans TFP colab .
Une autre façon d'utiliser les GP est en tant que modèle de variable latente : étant donné une collection d'observations de grande dimension (par exemple, des images), nous pouvons postuler une structure latente de basse dimension. Nous supposons que, conditionnellement à la structure latente, le grand nombre de sorties (pixels dans l'image) sont indépendants les uns des autres. La formation à ce modèle consiste à
- optimiser les paramètres du modèle (paramètres de la fonction noyau ainsi que, par exemple, la variance du bruit d'observation), et
- trouver, pour chaque observation d'apprentissage (image), un emplacement de point correspondant dans l'ensemble d'index. Toute l'optimisation peut être effectuée en maximisant la probabilité de log marginale des données.
Importations
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
%pylab inline
Populating the interactive namespace from numpy and matplotlib
Charger les données MNIST
# Load the MNIST data set and isolate a subset of it.
(x_train, y_train), (_, _) = tf.keras.datasets.mnist.load_data()
N = 1000
small_x_train = x_train[:N, ...].astype(np.float64) / 256.
small_y_train = y_train[:N]
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step 11501568/11490434 [==============================] - 0s 0us/step
Préparer des variables pouvant être entraînées
Nous entraînerons conjointement 3 paramètres du modèle ainsi que les entrées latentes.
# Create some trainable model parameters. We will constrain them to be strictly
# positive when constructing the kernel and the GP.
unconstrained_amplitude = tf.Variable(np.float64(1.), name='amplitude')
unconstrained_length_scale = tf.Variable(np.float64(1.), name='length_scale')
unconstrained_observation_noise = tf.Variable(np.float64(1.), name='observation_noise')
# We need to flatten the images and, somewhat unintuitively, transpose from
# shape [100, 784] to [784, 100]. This is because the 784 pixels will be
# treated as *independent* conditioned on the latent inputs, meaning we really
# have a batch of 784 GP's with 100 index_points.
observations_ = small_x_train.reshape(N, -1).transpose()
# Create a collection of N 2-dimensional index points that will represent our
# latent embeddings of the data. (Lawrence, 2004) prescribes initializing these
# with PCA, but a random initialization actually gives not-too-bad results, so
# we use this for simplicity. For a fun exercise, try doing the
# PCA-initialization yourself!
init_ = np.random.normal(size=(N, 2))
latent_index_points = tf.Variable(init_, name='latent_index_points')
Construire un modèle et des opérations d'entraînement
# Create our kernel and GP distribution
EPS = np.finfo(np.float64).eps
def create_kernel():
amplitude = tf.math.softplus(EPS + unconstrained_amplitude)
length_scale = tf.math.softplus(EPS + unconstrained_length_scale)
kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
return kernel
def loss_fn():
observation_noise_variance = tf.math.softplus(
EPS + unconstrained_observation_noise)
gp = tfd.GaussianProcess(
kernel=create_kernel(),
index_points=latent_index_points,
observation_noise_variance=observation_noise_variance)
log_probs = gp.log_prob(observations_, name='log_prob')
return -tf.reduce_mean(log_probs)
trainable_variables = [unconstrained_amplitude,
unconstrained_length_scale,
unconstrained_observation_noise,
latent_index_points]
optimizer = tf.optimizers.Adam(learning_rate=1.0)
@tf.function(autograph=False, jit_compile=True)
def train_model():
with tf.GradientTape() as tape:
loss_value = loss_fn()
grads = tape.gradient(loss_value, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss_value
Former et tracer les plongements latents résultants
# Initialize variables and train!
num_iters = 100
log_interval = 20
lips = np.zeros((num_iters, N, 2), np.float64)
for i in range(num_iters):
loss = train_model()
lips[i] = latent_index_points.numpy()
if i % log_interval == 0 or i + 1 == num_iters:
print("Loss at step %d: %f" % (i, loss))
Loss at step 0: 1108.121688 Loss at step 20: -159.633761 Loss at step 40: -263.014394 Loss at step 60: -283.713056 Loss at step 80: -288.709413 Loss at step 99: -289.662253
Tracer les résultats
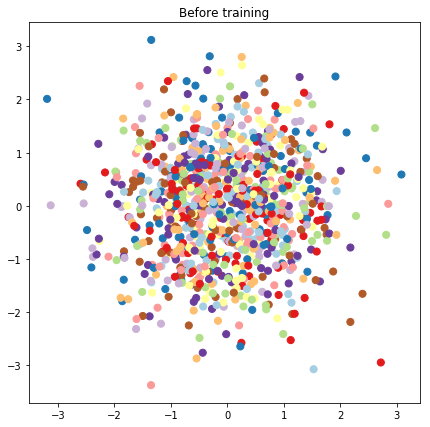
# Plot the latent locations before and after training
plt.figure(figsize=(7, 7))
plt.title("Before training")
plt.grid(False)
plt.scatter(x=init_[:, 0], y=init_[:, 1],
c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()
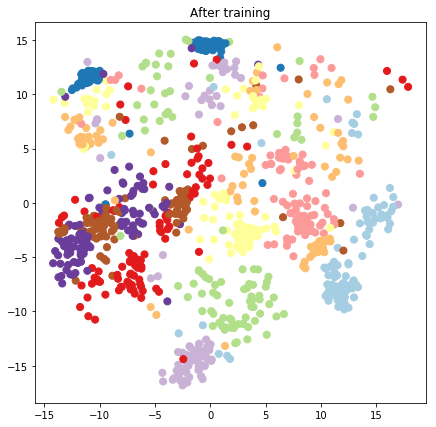
plt.figure(figsize=(7, 7))
plt.title("After training")
plt.grid(False)
plt.scatter(x=lips[-1, :, 0], y=lips[-1, :, 1],
c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()
Construire un modèle prédictif et des opérations d'échantillonnage
# We'll draw samples at evenly spaced points on a 10x10 grid in the latent
# input space.
sample_grid_points = 10
grid_ = np.linspace(-4, 4, sample_grid_points).astype(np.float64)
# Create a 10x10 grid of 2-vectors, for a total shape [10, 10, 2]
grid_ = np.stack(np.meshgrid(grid_, grid_), axis=-1)
# This part's a bit subtle! What we defined above was a batch of 784 (=28x28)
# independent GP distributions over the input space. Each one corresponds to a
# single pixel of an MNIST image. Now what we'd like to do is draw 100 (=10x10)
# *independent* samples, each one separately conditioned on all the observations
# as well as the learned latent input locations above.
#
# The GP regression model below will define a batch of 784 independent
# posteriors. We'd like to get 100 independent samples each at a different
# latent index point. We could loop over the points in the grid, but that might
# be a bit slow. Instead, we can vectorize the computation by tacking on *even
# more* batch dimensions to our GaussianProcessRegressionModel distribution.
# In the below grid_ shape, we have concatentaed
# 1. batch shape: [sample_grid_points, sample_grid_points, 1]
# 2. number of examples: [1]
# 3. number of latent input dimensions: [2]
# The `1` in the batch shape will broadcast with 784. The final result will be
# samples of shape [10, 10, 784, 1]. The `1` comes from the "number of examples"
# and we can just `np.squeeze` it off.
grid_ = grid_.reshape(sample_grid_points, sample_grid_points, 1, 1, 2)
# Create the GPRegressionModel instance which represents the posterior
# predictive at the grid of new points.
gprm = tfd.GaussianProcessRegressionModel(
kernel=create_kernel(),
# Shape [10, 10, 1, 1, 2]
index_points=grid_,
# Shape [1000, 2]. 1000 2 dimensional vectors.
observation_index_points=latent_index_points,
# Shape [784, 1000]. A batch of 784 1000-dimensional observations.
observations=observations_)
Tirer des échantillons conditionnés par les données et les plongements latents
Nous échantillonnons en 100 points sur une grille 2D dans l'espace latent.
samples = gprm.sample()
# Plot the grid of samples at new points. We do a bit of tweaking of the samples
# first, squeezing off extra 1-shapes and normalizing the values.
samples_ = np.squeeze(samples.numpy())
samples_ = ((samples_ -
samples_.min(-1, keepdims=True)) /
(samples_.max(-1, keepdims=True) -
samples_.min(-1, keepdims=True)))
samples_ = samples_.reshape(sample_grid_points, sample_grid_points, 28, 28)
samples_ = samples_.transpose([0, 2, 1, 3])
samples_ = samples_.reshape(28 * sample_grid_points, 28 * sample_grid_points)
plt.figure(figsize=(7, 7))
ax = plt.subplot()
ax.grid(False)
ax.imshow(-samples_, interpolation='none', cmap='Greys')
plt.show()

Conclusion
Nous avons fait une brève visite guidée du modèle de variable latente du processus gaussien et montré comment nous pouvons l'implémenter en quelques lignes de code TF et TF Probability.
