 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
En esta colaboración, exploramos la regresión del proceso gaussiano usando TensorFlow y TensorFlow Probability. Generamos algunas observaciones ruidosas de algunas funciones conocidas y ajustamos modelos GP a esos datos. Luego tomamos muestras de la parte posterior de GP y trazamos los valores de función muestreados sobre cuadrículas en sus dominios.
Fondo
Deje \(\mathcal{X}\) cualquier conjunto. Un proceso Gaussiano (GP) es una colección de variables aleatorias indexadas por \(\mathcal{X}\) tal que si\(\{X_1, \ldots, X_n\} \subset \mathcal{X}\) es cualquier subconjunto finito, la densidad marginal\(p(X_1 = x_1, \ldots, X_n = x_n)\) es multivariante gaussiana. Cualquier distribución gaussiana está completamente especificada por su primer y segundo momento central (media y covarianza), y las GP no son una excepción. Podemos especificar un GP por completo en términos de su función de medio \(\mu : \mathcal{X} \to \mathbb{R}\) y covarianza función\(k : \mathcal{X} \times \mathcal{X} \to \mathbb{R}\). La mayor parte del poder expresivo de los GP está encapsulado en la elección de la función de covarianza. Por diversas razones, la función de covarianza también se conoce como una función del núcleo. Se requiere sólo para ser simétrica y definida positiva (véase Ch. 4 de Rasmussen & Williams ). A continuación hacemos uso del núcleo de covarianza ExponentiatedQuadratic. su forma es
\[ k(x, x') := \sigma^2 \exp \left( \frac{\|x - x'\|^2}{\lambda^2} \right) \]
donde \(\sigma^2\) se llama la 'amplitud' y \(\lambda\) la escala de longitud. Los parámetros del núcleo se pueden seleccionar a través de un procedimiento de optimización de máxima verosimilitud.
Una muestra completa de un GP comprende una función de valor real sobre el espacio entero\(\mathcal{X}\) y es en la práctica poco práctico de realizar; a menudo, uno elige un conjunto de puntos en los que observar una muestra y dibuja valores de función en estos puntos. Esto se logra mediante el muestreo de una Gaussiana multivariante apropiada (de dimensión finita).
Tenga en cuenta que, de acuerdo con la definición anterior, cualquier distribución gaussiana multivariante de dimensión finita también es un proceso gaussiano. Por lo general, cuando uno se refiere a un médico de cabecera, está implícito que el conjunto índice es cierta \(\mathbb{R}^n\)y que de hecho hará que esta suposición aquí.
Una aplicación común de los procesos gaussianos en el aprendizaje automático es la regresión de procesos gaussianos. La idea es que deseamos estimar una función desconocida observaciones ruidosas dados \(\{y_1, \ldots, y_N\}\) de la función en un número finito de puntos \(\{x_1, \ldots x_N\}.\) Nos imaginamos un proceso generativo
\[ \begin{align} f \sim \: & \textsf{GaussianProcess}\left( \text{mean_fn}=\mu(x), \text{covariance_fn}=k(x, x')\right) \\ y_i \sim \: & \textsf{Normal}\left( \text{loc}=f(x_i), \text{scale}=\sigma\right), i = 1, \ldots, N \end{align} \]
Como se señaló anteriormente, la función muestreada es imposible de calcular, ya que requeriríamos su valor en un número infinito de puntos. En cambio, se considera una muestra finita de una Gaussiana multivariada.
\[ \begin{gather} \begin{bmatrix} f(x_1) \\ \vdots \\ f(x_N) \end{bmatrix} \sim \textsf{MultivariateNormal} \left( \: \text{loc}= \begin{bmatrix} \mu(x_1) \\ \vdots \\ \mu(x_N) \end{bmatrix} \:,\: \text{scale}= \begin{bmatrix} k(x_1, x_1) & \cdots & k(x_1, x_N) \\ \vdots & \ddots & \vdots \\ k(x_N, x_1) & \cdots & k(x_N, x_N) \\ \end{bmatrix}^{1/2} \: \right) \end{gather} \\ y_i \sim \textsf{Normal} \left( \text{loc}=f(x_i), \text{scale}=\sigma \right) \]
Tenga en cuenta que el exponente \(\frac{1}{2}\) en la matriz de covarianza: esto denota una descomposición de Cholesky. Es necesario calcular el Cholesky porque el MVN es una distribución familiar a escala de ubicación. Por desgracia, la descomposición de Cholesky es computacionalmente caro, teniendo \(O(N^3)\) tiempo y \(O(N^2)\) espacio. Gran parte de la literatura GP se centra en tratar con este pequeño exponente aparentemente inocuo.
Es común tomar la función media anterior como constante, a menudo cero. Además, algunas convenciones de notación son convenientes. A menudo se escribe \(\mathbf{f}\) para el vector finito de valores de la función de la muestra. Un número de notaciones interesantes se utilizan para la matriz de covarianza resultante de la aplicación de \(k\) a pares de entradas. Siguiendo (Quiñonero-Candela, 2005) , observamos que los componentes de la matriz son covarianzas de valores de la función en los puntos de entrada particulares. Así podemos denotamos la matriz de covarianza como \(K_{AB}\)donde \(A\) y \(B\) son algunos indicadores de la colección de valores de la función a lo largo de las dimensiones de la matriz dados.
Por ejemplo, teniendo en cuenta los datos observados \((\mathbf{x}, \mathbf{y})\) con valores de función latente implícitas \(\mathbf{f}\), podemos escribir
\[ K_{\mathbf{f},\mathbf{f} } = \begin{bmatrix} k(x_1, x_1) & \cdots & k(x_1, x_N) \\ \vdots & \ddots & \vdots \\ k(x_N, x_1) & \cdots & k(x_N, x_N) \\ \end{bmatrix} \]
De manera similar, podemos mezclar conjuntos de entradas, como en
\[ K_{\mathbf{f},*} = \begin{bmatrix} k(x_1, x^*_1) & \cdots & k(x_1, x^*_T) \\ \vdots & \ddots & \vdots \\ k(x_N, x^*_1) & \cdots & k(x_N, x^*_T) \\ \end{bmatrix} \]
donde suponemos que hay \(N\) entradas de entrenamiento, y \(T\) entradas de prueba. El proceso generativo anterior se puede escribir de forma compacta como
\[ \begin{align} \mathbf{f} \sim \: & \textsf{MultivariateNormal} \left( \text{loc}=\mathbf{0}, \text{scale}=K_{\mathbf{f},\mathbf{f} }^{1/2} \right) \\ y_i \sim \: & \textsf{Normal} \left( \text{loc}=f_i, \text{scale}=\sigma \right), i = 1, \ldots, N \end{align} \]
La operación de muestreo en la primera línea se obtiene un conjunto finito de \(N\) valores de la función de una gaussiana multivariante - no una función entera como en la notación anterior GP dibujar. La segunda línea describe una colección de \(N\) extrae de gaussianas univariantes centrado en los diversos valores de la función, con el ruido de observación fijo \(\sigma^2\).
Con el modelo generativo anterior en su lugar, podemos proceder a considerar el problema de inferencia posterior. Esto produce una distribución posterior sobre los valores de función en un nuevo conjunto de puntos de prueba, condicionada por los datos con ruido observados del proceso anterior.
Con la notación anterior en su lugar, podemos escribir de forma compacta la distribución posterior de predicción sobre el futuro (ruidoso) observaciones condicionada a las entradas y los datos de entrenamiento correspondiente de la siguiente manera (para más detalles, véase el § 2.2 de Rasmussen & Williams ).
\[ \mathbf{y}^* \mid \mathbf{x}^*, \mathbf{x}, \mathbf{y} \sim \textsf{Normal} \left( \text{loc}=\mathbf{\mu}^*, \text{scale}=(\Sigma^*)^{1/2} \right), \]
donde
\[ \mathbf{\mu}^* = K_{*,\mathbf{f} }\left(K_{\mathbf{f},\mathbf{f} } + \sigma^2 I \right)^{-1} \mathbf{y} \]
y
\[ \Sigma^* = K_{*,*} - K_{*,\mathbf{f} } \left(K_{\mathbf{f},\mathbf{f} } + \sigma^2 I \right)^{-1} K_{\mathbf{f},*} \]
Importaciones
import time
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
tfb = tfp.bijectors
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
tf.enable_v2_behavior()
from mpl_toolkits.mplot3d import Axes3D
%pylab inline
# Configure plot defaults
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['grid.color'] = '#666666'
%config InlineBackend.figure_format = 'png'
Populating the interactive namespace from numpy and matplotlib
Ejemplo: Regresión de GP exacta en datos sinusoidales ruidosos
Aquí generamos datos de entrenamiento a partir de una sinusoide ruidosa, luego muestreamos un montón de curvas de la parte posterior del modelo de regresión GP. Utilizamos Adam para optimizar los hiperparámetros del kernel (se minimiza la probabilidad log negativo de los datos en virtud de la anterior). Trazamos la curva de entrenamiento, seguida de la función verdadera y las muestras posteriores.
def sinusoid(x):
return np.sin(3 * np.pi * x[..., 0])
def generate_1d_data(num_training_points, observation_noise_variance):
"""Generate noisy sinusoidal observations at a random set of points.
Returns:
observation_index_points, observations
"""
index_points_ = np.random.uniform(-1., 1., (num_training_points, 1))
index_points_ = index_points_.astype(np.float64)
# y = f(x) + noise
observations_ = (sinusoid(index_points_) +
np.random.normal(loc=0,
scale=np.sqrt(observation_noise_variance),
size=(num_training_points)))
return index_points_, observations_
# Generate training data with a known noise level (we'll later try to recover
# this value from the data).
NUM_TRAINING_POINTS = 100
observation_index_points_, observations_ = generate_1d_data(
num_training_points=NUM_TRAINING_POINTS,
observation_noise_variance=.1)
Pondremos priores en los hiperparámetros del núcleo, y escribimos la distribución conjunta de los hiperparámetros y los datos observados utilizando tfd.JointDistributionNamed .
def build_gp(amplitude, length_scale, observation_noise_variance):
"""Defines the conditional dist. of GP outputs, given kernel parameters."""
# Create the covariance kernel, which will be shared between the prior (which we
# use for maximum likelihood training) and the posterior (which we use for
# posterior predictive sampling)
kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
# Create the GP prior distribution, which we will use to train the model
# parameters.
return tfd.GaussianProcess(
kernel=kernel,
index_points=observation_index_points_,
observation_noise_variance=observation_noise_variance)
gp_joint_model = tfd.JointDistributionNamed({
'amplitude': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'length_scale': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'observation_noise_variance': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'observations': build_gp,
})
Podemos verificar la cordura de nuestra implementación al verificar que podemos tomar muestras de la anterior y calcular la densidad de registro de una muestra.
x = gp_joint_model.sample()
lp = gp_joint_model.log_prob(x)
print("sampled {}".format(x))
print("log_prob of sample: {}".format(lp))
sampled {'observation_noise_variance': <tf.Tensor: shape=(), dtype=float64, numpy=2.067952217184325>, 'length_scale': <tf.Tensor: shape=(), dtype=float64, numpy=1.154435715487831>, 'amplitude': <tf.Tensor: shape=(), dtype=float64, numpy=5.383850737703549>, 'observations': <tf.Tensor: shape=(100,), dtype=float64, numpy=
array([-2.37070577, -2.05363838, -0.95152824, 3.73509388, -0.2912646 ,
0.46112342, -1.98018513, -2.10295857, -1.33589756, -2.23027226,
-2.25081374, -0.89450835, -2.54196452, 1.46621647, 2.32016193,
5.82399989, 2.27241034, -0.67523432, -1.89150197, -1.39834474,
-2.33954116, 0.7785609 , -1.42763627, -0.57389025, -0.18226098,
-3.45098732, 0.27986652, -3.64532398, -1.28635204, -2.42362875,
0.01107288, -2.53222176, -2.0886136 , -5.54047694, -2.18389607,
-1.11665628, -3.07161217, -2.06070336, -0.84464262, 1.29238438,
-0.64973999, -2.63805504, -3.93317576, 0.65546645, 2.24721181,
-0.73403676, 5.31628298, -1.2208384 , 4.77782252, -1.42978168,
-3.3089274 , 3.25370494, 3.02117591, -1.54862932, -1.07360811,
1.2004856 , -4.3017773 , -4.95787789, -1.95245901, -2.15960839,
-3.78592731, -1.74096185, 3.54891595, 0.56294143, 1.15288455,
-0.77323696, 2.34430694, -1.05302007, -0.7514684 , -0.98321063,
-3.01300144, -3.00033274, 0.44200837, 0.45060886, -1.84497318,
-1.89616746, -2.15647664, -2.65672581, -3.65493379, 1.70923375,
-3.88695218, -0.05151283, 4.51906677, -2.28117003, 3.03032793,
-1.47713194, -0.35625273, 3.73501587, -2.09328047, -0.60665614,
-0.78177188, -0.67298545, 2.97436033, -0.29407932, 2.98482427,
-1.54951178, 2.79206821, 4.2225733 , 2.56265198, 2.80373284])>}
log_prob of sample: -194.96442183797524
Ahora vamos a optimizar para encontrar los valores de los parámetros con la probabilidad posterior más alta. Definiremos una variable para cada parámetro y restringiremos sus valores para que sean positivos.
# Create the trainable model parameters, which we'll subsequently optimize.
# Note that we constrain them to be strictly positive.
constrain_positive = tfb.Shift(np.finfo(np.float64).tiny)(tfb.Exp())
amplitude_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='amplitude',
dtype=np.float64)
length_scale_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='length_scale',
dtype=np.float64)
observation_noise_variance_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='observation_noise_variance_var',
dtype=np.float64)
trainable_variables = [v.trainable_variables[0] for v in
[amplitude_var,
length_scale_var,
observation_noise_variance_var]]
Para acondicionar el modelo en nuestros datos observados, vamos a definir un target_log_prob función, lo que lleva a los (aún no se ha inferido) hiperparámetros del núcleo.
def target_log_prob(amplitude, length_scale, observation_noise_variance):
return gp_joint_model.log_prob({
'amplitude': amplitude,
'length_scale': length_scale,
'observation_noise_variance': observation_noise_variance,
'observations': observations_
})
# Now we optimize the model parameters.
num_iters = 1000
optimizer = tf.optimizers.Adam(learning_rate=.01)
# Use `tf.function` to trace the loss for more efficient evaluation.
@tf.function(autograph=False, jit_compile=False)
def train_model():
with tf.GradientTape() as tape:
loss = -target_log_prob(amplitude_var, length_scale_var,
observation_noise_variance_var)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
# Store the likelihood values during training, so we can plot the progress
lls_ = np.zeros(num_iters, np.float64)
for i in range(num_iters):
loss = train_model()
lls_[i] = loss
print('Trained parameters:')
print('amplitude: {}'.format(amplitude_var._value().numpy()))
print('length_scale: {}'.format(length_scale_var._value().numpy()))
print('observation_noise_variance: {}'.format(observation_noise_variance_var._value().numpy()))
Trained parameters: amplitude: 0.9176153445125278 length_scale: 0.18444082442910079 observation_noise_variance: 0.0880273312850989
# Plot the loss evolution
plt.figure(figsize=(12, 4))
plt.plot(lls_)
plt.xlabel("Training iteration")
plt.ylabel("Log marginal likelihood")
plt.show()

# Having trained the model, we'd like to sample from the posterior conditioned
# on observations. We'd like the samples to be at points other than the training
# inputs.
predictive_index_points_ = np.linspace(-1.2, 1.2, 200, dtype=np.float64)
# Reshape to [200, 1] -- 1 is the dimensionality of the feature space.
predictive_index_points_ = predictive_index_points_[..., np.newaxis]
optimized_kernel = tfk.ExponentiatedQuadratic(amplitude_var, length_scale_var)
gprm = tfd.GaussianProcessRegressionModel(
kernel=optimized_kernel,
index_points=predictive_index_points_,
observation_index_points=observation_index_points_,
observations=observations_,
observation_noise_variance=observation_noise_variance_var,
predictive_noise_variance=0.)
# Create op to draw 50 independent samples, each of which is a *joint* draw
# from the posterior at the predictive_index_points_. Since we have 200 input
# locations as defined above, this posterior distribution over corresponding
# function values is a 200-dimensional multivariate Gaussian distribution!
num_samples = 50
samples = gprm.sample(num_samples)
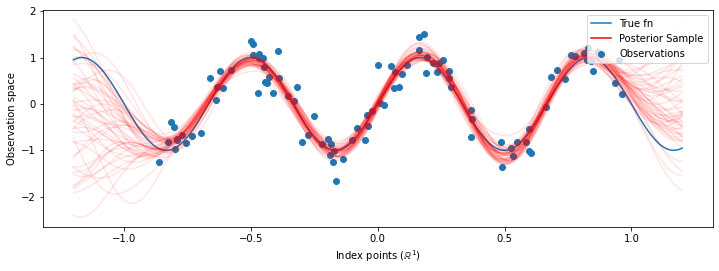
# Plot the true function, observations, and posterior samples.
plt.figure(figsize=(12, 4))
plt.plot(predictive_index_points_, sinusoid(predictive_index_points_),
label='True fn')
plt.scatter(observation_index_points_[:, 0], observations_,
label='Observations')
for i in range(num_samples):
plt.plot(predictive_index_points_, samples[i, :], c='r', alpha=.1,
label='Posterior Sample' if i == 0 else None)
leg = plt.legend(loc='upper right')
for lh in leg.legendHandles:
lh.set_alpha(1)
plt.xlabel(r"Index points ($\mathbb{R}^1$)")
plt.ylabel("Observation space")
plt.show()
Marginación de hiperparámetros con HMC
En lugar de optimizar los hiperparámetros, intentemos integrarlos con el hamiltoniano Monte Carlo. Primero definiremos y ejecutaremos un muestreador para extraer aproximadamente de la distribución posterior sobre los hiperparámetros del kernel, dadas las observaciones.
num_results = 100
num_burnin_steps = 50
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=target_log_prob,
step_size=tf.cast(0.1, tf.float64)),
bijector=[constrain_positive, constrain_positive, constrain_positive])
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=tf.cast(0.75, tf.float64))
initial_state = [tf.cast(x, tf.float64) for x in [1., 1., 1.]]
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=False)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps,
trace_fn=lambda current_state, kernel_results: kernel_results)
t0 = time.time()
samples, kernel_results = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 9.00s.
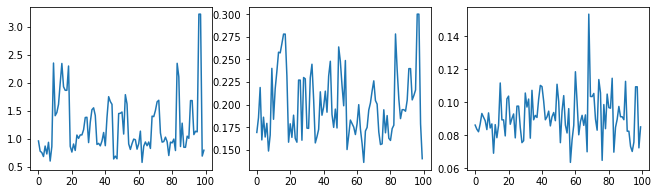
Revisemos la cordura del muestreador examinando los rastros de hiperparámetros.
(amplitude_samples,
length_scale_samples,
observation_noise_variance_samples) = samples
f = plt.figure(figsize=[15, 3])
for i, s in enumerate(samples):
ax = f.add_subplot(1, len(samples) + 1, i + 1)
ax.plot(s)
Ahora, en lugar de construir un solo GP con los hiperparámetros optimizados, construimos la distribución posterior predictiva como una mezcla de los médicos, cada uno definido por una muestra de la distribución posterior sobre hiperparámetros. Esto se integra aproximadamente sobre los parámetros posteriores a través del muestreo de Monte Carlo para calcular la distribución predictiva marginal en ubicaciones no observadas.
# The sampled hyperparams have a leading batch dimension, `[num_results, ...]`,
# so they construct a *batch* of kernels.
batch_of_posterior_kernels = tfk.ExponentiatedQuadratic(
amplitude_samples, length_scale_samples)
# The batch of kernels creates a batch of GP predictive models, one for each
# posterior sample.
batch_gprm = tfd.GaussianProcessRegressionModel(
kernel=batch_of_posterior_kernels,
index_points=predictive_index_points_,
observation_index_points=observation_index_points_,
observations=observations_,
observation_noise_variance=observation_noise_variance_samples,
predictive_noise_variance=0.)
# To construct the marginal predictive distribution, we average with uniform
# weight over the posterior samples.
predictive_gprm = tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(logits=tf.zeros([num_results])),
components_distribution=batch_gprm)
num_samples = 50
samples = predictive_gprm.sample(num_samples)
# Plot the true function, observations, and posterior samples.
plt.figure(figsize=(12, 4))
plt.plot(predictive_index_points_, sinusoid(predictive_index_points_),
label='True fn')
plt.scatter(observation_index_points_[:, 0], observations_,
label='Observations')
for i in range(num_samples):
plt.plot(predictive_index_points_, samples[i, :], c='r', alpha=.1,
label='Posterior Sample' if i == 0 else None)
leg = plt.legend(loc='upper right')
for lh in leg.legendHandles:
lh.set_alpha(1)
plt.xlabel(r"Index points ($\mathbb{R}^1$)")
plt.ylabel("Observation space")
plt.show()
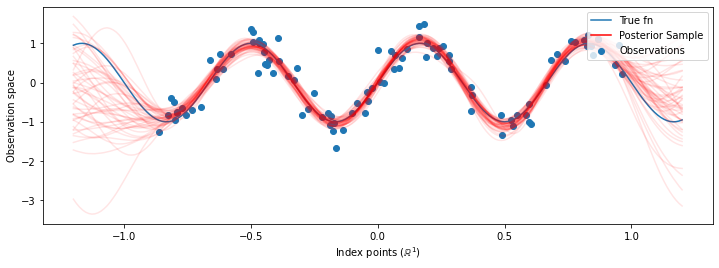
Aunque las diferencias son sutiles en este caso, en general, esperaríamos que la distribución predictiva posterior se generalizara mejor (dara una mayor probabilidad a los datos retenidos) que simplemente usando los parámetros más probables como hicimos anteriormente.
