Ajustement de modèles linéaires généralisés à effets mixtes à l'aide de l'inférence variationnelle

Voir sur TensorFlow.org Exécuter dans Google Colab Voir la source sur GitHub Télécharger le cahier

Installer

Installer

Résumé

Dans cette collaboration, nous montrons comment ajuster un modèle linéaire généralisé à effets mixtes à l'aide de l'inférence variationnelle dans TensorFlow Probability.

Famille de modèles

Généralisée modèles à effets mixtes linéaires (GLMM) sont similaires à modèles linéaires généralisés (GLM) sauf qu'ils comportent un bruit spécifique de l' échantillon dans la réponse linéaire prédite. Ceci est utile en partie car cela permet aux fonctionnalités rarement vues de partager des informations avec des fonctionnalités plus fréquemment vues.

En tant que processus génératif, un modèle linéaire généralisé à effets mixtes (GLMM) se caractérise par :

\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]

où:

\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]

En d' autres termes, il dit que toutes les catégories de chaque groupe est associé à un échantillon, \(\beta_{rc}\), à partir d' une normale à plusieurs variables. Bien que le \(\beta_{rc}\) tirages sont toujours indépendants, ils ne sont indentically distribués pour un groupe \(r\): avis il y a exactement un \(\Sigma_r\) pour chaque \(r\in\{1,\ldots,R\}\).

Lorsque affine combinée avec les caractéristiques de groupe d'un échantillon (\(z_{r,i}\)), le résultat est le bruit de spécifique à l' échantillon sur la \(i\)-ième prédit réponse linéaire (qui est par ailleurs \(x_i^\top\omega\)).

Lorsque nous estimons \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) nous essentiellement estimer la quantité de bruit d' un groupe à effet aléatoire porte qui autrement se noient le signal présent dans \(x_i^\top\omega\).

Il existe une variété d'options pour la \(\text{Distribution}\) et fonction de lien inverse , \(g^{-1}\). Les choix courants sont :

  • \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
  • \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), et,
  • \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).

Pour plus de possibilités, voir le tfp.glm module.

Inférence variationnelle

Malheureusement, la recherche des estimations du maximum de vraisemblance des paramètres \(\beta,\{\Sigma_r\}_r^R\) entraîne une intégrale non analytique. Pour contourner ce problème, nous avons plutôt

  1. Définir une famille paramétrée de distributions (la « densité de substitution »), notée \(q_{\lambda}\) en annexe.
  2. Trouver des paramètres \(\lambda\) afin que \(q_{\lambda}\) est proche de notre véritable denstiy cible.

La famille des distributions sera gaussiennes indépendantes des dimensions appropriées, et par « proche de notre densité cible », nous dire « minimiser la divergence de Kullback-Leibler ». Voir, par exemple la section 2.2 de « Variational Inference: Un examen pour Statisticiens » pour une dérivation bien écrit et la motivation. En particulier, il montre que minimiser la divergence KL équivaut à minimiser la limite inférieure des preuves négatives (ELBO).

Problème de jouet

Gelman et al. De (2007) « ensemble de données radon » est un ensemble de données parfois utilisé pour démontrer des approches de régression. (Par exemple, ce étroitement lié blog post PyMC3 .) L'ensemble de données de radon contient des mesures intérieures de radon prises aux États-Unis. Le radon est naturellement ocurring gaz radioactif qui est toxique à des concentrations élevées.

Pour notre démonstration, supposons que l'on s'intéresse à valider l'hypothèse que les niveaux de Radon sont plus élevés dans les ménages comportant un sous-sol. Nous soupçonnons également que la concentration de radon est liée au type de sol, c'est-à-dire à la géographie.

Pour présenter cela comme un problème de ML, nous essaierons de prédire les niveaux de log-radon en fonction d'une fonction linéaire du sol sur lequel la lecture a été effectuée. Nous utiliserons également le comté comme effet aléatoire et, ce faisant, nous prendrons en compte les écarts dus à la géographie. En d' autres termes, nous allons utiliser un modèle à effet mixte linéaire généralisé .

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import os
from six.moves import urllib

import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

Nous allons également vérifier rapidement la disponibilité d'un GPU :

if tf.test.gpu_device_name() != '/device:GPU:0':
  print("We'll just use the CPU for this run.")
else:
  print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))

We'll just use the CPU for this run.

Obtenir l'ensemble de données :

Nous chargeons l'ensemble de données à partir des ensembles de données TensorFlow et effectuons un léger prétraitement.

def load_and_preprocess_radon_dataset(state='MN'):
  """Load the Radon dataset from TensorFlow Datasets and preprocess it.

  Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
  to Minnesota data and preprocess to obtain the following features:
  - `county`: Name of county in which the measurement was taken.
  - `floor`: Floor of house (0 for basement, 1 for first floor) on which the
    measurement was taken.

  The target variable is `log_radon`, the log of the Radon measurement in the
  house.
  """
  ds = tfds.load('radon', split='train')
  radon_data = tfds.as_dataframe(ds)
  radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
  df = radon_data[radon_data.state==state.encode()].copy()

  df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
  # Make county names look nice. 
  df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
  # Remap categories to start from 0 and end at max(category).
  df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
  df['county_code'] = df.county.cat.codes
  # Radon levels are all positive, but log levels are unconstrained
  df['log_radon'] = df['radon'].apply(np.log)

  # Drop columns we won't use and tidy the index 
  columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
  df = df[columns_to_keep].reset_index(drop=True)

  return df

df = load_and_preprocess_radon_dataset()
df.head()

Spécialisation de la famille GLMM

Dans cette section, nous spécialisons la famille GLMM à la tâche de prédire les niveaux de radon. Pour ce faire, considérons d'abord le cas particulier à effet fixe d'un GLMM :

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]

Ce modèle postule que le radon journal dans l' observation \(j\) est (dans l' attente) régies par le plancher du \(j\)e lecture est prise, plus une interception constante. En pseudocode, on pourrait écrire

def estimate_log_radon(floor):
    return intercept + floor_effect[floor]

il y a un poids appris pour chaque étage et universel intercept terme. En regardant les mesures de radon des étages 0 et 1, il semble que cela pourrait être un bon début :

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')

df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");

png

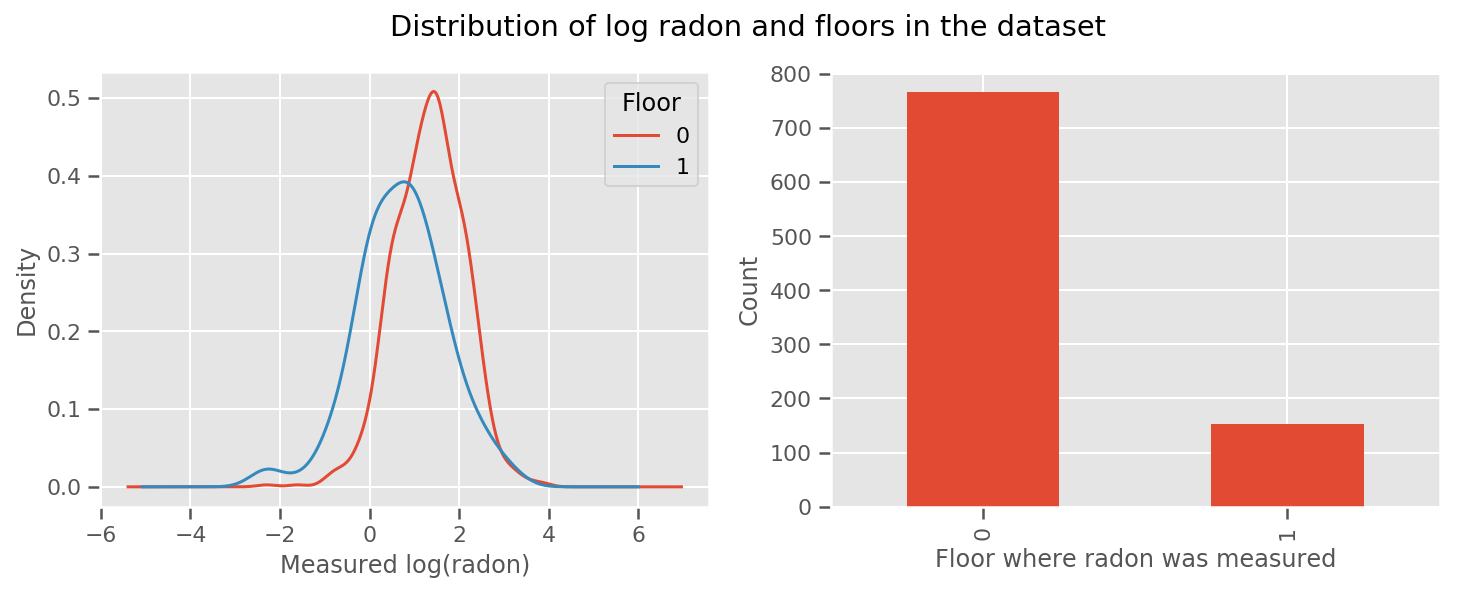
Pour rendre le modèle un peu plus sophistiqué, y compris quelque chose sur la géographie, c'est probablement encore mieux : le radon fait partie de la chaîne de désintégration de l'uranium, qui peut être présent dans le sol, la géographie semble donc essentielle à prendre en compte.

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]

Encore une fois, en pseudocode, nous avons

def estimate_log_radon(floor, county):
    return intercept + floor_effect[floor] + county_effect[county]

le même que précédemment, sauf avec un poids spécifique au comté.

Compte tenu d'un ensemble d'entraînement suffisamment grand, il s'agit d'un modèle raisonnable. Cependant, étant donné nos données du Minnesota, nous voyons qu'il y a un grand nombre de comtés avec un petit nombre de mesures. Par exemple, 39 des 85 comtés ont moins de cinq observations.

Cela motive le partage de la force statistique entre toutes nos observations, d'une manière qui converge vers le modèle ci-dessus à mesure que le nombre d'observations par comté augmente.

fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');

png

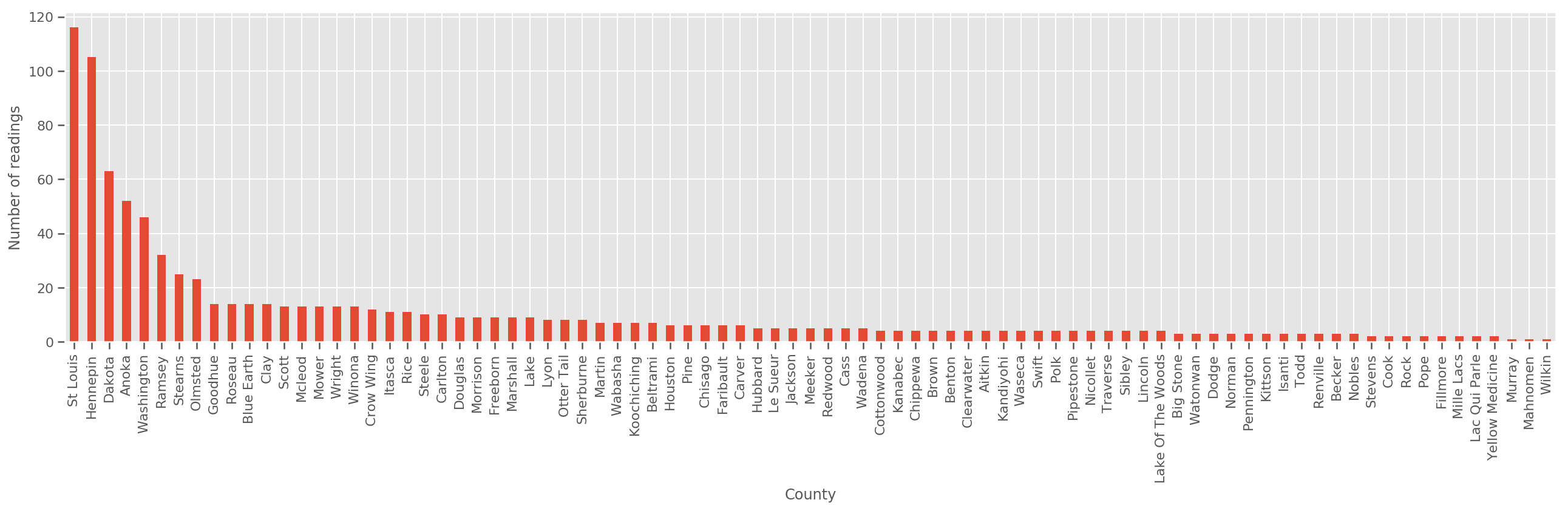
Si nous nous situons ce modèle, le county_effect vecteur finirait probablement par mémoriser les résultats pour les comtés qui avaient seulement quelques échantillons de formation, peut - être surapprentissage et conduisant à une généralisation médiocre.

Les GLMM offrent un juste milieu aux deux GLM ci-dessus. Nous pourrions envisager d'adapter

\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]

Ce modèle est le même que le premier, mais nous avons fixé nos chances d'être une distribution normale, et partagera la variance dans tous les comtés à travers la variable (unique) county_scale . En pseudo-code,

def estimate_log_radon(floor, county):
    county_mean = county_effect[county]
    random_effect = np.random.normal() * county_scale + county_mean
    return intercept + floor_effect[floor] + random_effect

Nous allons déduire la distribution conjointe sur county_scale , county_mean et le random_effect en utilisant nos données observées. Le monde county_scale nous permet de partager la force statistique entre les comtés: ceux qui ont de nombreuses observations donner un coup à l'écart des comtés avec quelques observations. De plus, à mesure que nous recueillons plus de données, ce modèle convergera vers le modèle sans variable d'échelle regroupée - même avec cet ensemble de données, nous arriverons à des conclusions similaires sur les comtés les plus observés avec l'un ou l'autre modèle.

Expérience

Nous allons maintenant essayer d'adapter le GLMM ci-dessus en utilisant l'inférence variationnelle dans TensorFlow. Nous allons d'abord diviser les données en entités et en libellés.

features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()

Spécifier le modèle

def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):

  def model():
    county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
    intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
    floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
    county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
                                    scale=county_scale,
                                    name='county_prior')
    random_effect = tf.gather(county_prior, county, axis=-1)

    fixed_effect = intercept + floor_weight * floor
    linear_response = fixed_effect + random_effect
    yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
  return tfd.JointDistributionCoroutineAutoBatched(model)

joint = make_joint_distribution_coroutine(
    features.floor.values, features.county_code.values, df.county.nunique(),
    df.floor.nunique())

# Define a closure over the joint distribution 
# to condition on the observed labels.
def target_log_prob_fn(*args):
  return joint.log_prob(*args, likelihood=labels)

Spécifier la substitution postérieure

Nous Compilez une famille de substitution \(q_{\lambda}\), où les paramètres \(\lambda\) sont trainable. Dans ce cas, notre famille est une distribution normale à plusieurs variables indépendantes, une pour chaque paramètre, et \(\lambda = \{(\mu_j, \sigma_j)\}\), où \(j\) indexe les quatre paramètres.

La méthode que nous utilisons pour adapter les usages famille de substitution tf.Variables . Nous utilisons également tfp.util.TransformedVariable avec Softplus pour contraindre les paramètres d'échelle (trainable) positif. De plus, nous appliquons Softplus à l'ensemble scale_prior , qui est un paramètre positif.

Nous initialisons ces variables pouvant être entraînées avec un peu de gigue pour faciliter l'optimisation.

# Initialize locations and scales randomly with `tf.Variable`s and 
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
    tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
    initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
    bijector=tfb.Softplus())
n_counties = df.county.nunique()

surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
  tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())),           # scale_prior
  tfd.Normal(_init_loc(), _init_scale()),                           # intercept
  tfd.Normal(_init_loc(), _init_scale()),                           # floor_weight
  tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))])  # county_prior

Notez que cette cellule peut être remplacé par tfp.experimental.vi.build_factored_surrogate_posterior , comme dans:

surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
  event_shape=joint.event_shape_tensor()[:-1],
  constraining_bijectors=[tfb.Softplus(), None, None, None])

Résultats

Rappelez-vous que notre objectif est de définir une famille de distributions paramétrable et traitable, puis de sélectionner des paramètres de sorte que nous ayons une distribution traitable qui soit proche de notre distribution cible.

Nous avons construit la distribution de substitution ci - dessus, et peut utiliser tfp.vi.fit_surrogate_posterior , qui accepte un optimiseur et un certain nombre d'étapes pour trouver les paramètres du modèle de substitution réduisant au minimum la ELBO négative (qui corresonds à minimiser la divergence Kullback-Liebler entre la mère porteuse et la distribution cible).

La valeur de retour est le ELBO négatif à chaque étape, et les distributions en surrogate_posterior aura été mis à jour avec les paramètres trouvés par l'optimiseur.

optimizer = tf.optimizers.Adam(learning_rate=1e-2)

losses = tfp.vi.fit_surrogate_posterior(
    target_log_prob_fn, 
    surrogate_posterior,
    optimizer=optimizer,
    num_steps=3000, 
    seed=42,
    sample_size=2)

(scale_prior_, 
 intercept_, 
 floor_weight_, 
 county_weights_), _ = surrogate_posterior.sample_distributions()

print('        intercept (mean): ', intercept_.mean())
print('     floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))

intercept (mean):  tf.Tensor(1.4352839, shape=(), dtype=float32)
     floor_weight (mean):  tf.Tensor(-0.6701997, shape=(), dtype=float32)
 scale_prior (approx. mean):  tf.Tensor(0.28682157, shape=(), dtype=float32)

fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
       ylabel="Loss (ELBO)",
       title="Loss during training",
       ylim=0);

png

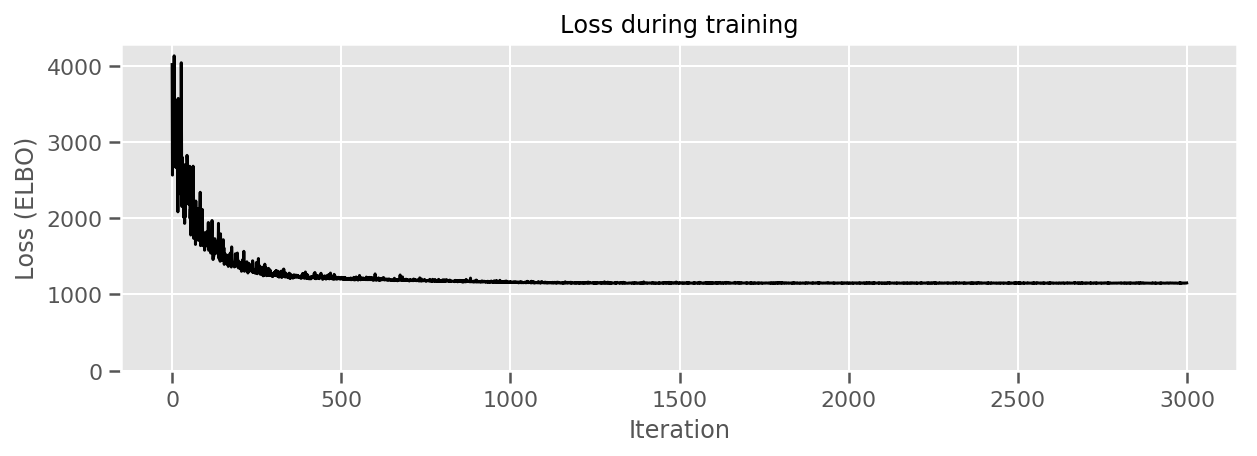
Nous pouvons tracer les effets de comté moyens estimés, ainsi que l'incertitude de cette moyenne. Nous avons classé cela par nombre d'observations, avec la plus grande à gauche. Notez que l'incertitude est faible pour les comtés avec de nombreuses observations, mais est plus grande pour les comtés qui n'ont qu'une ou deux observations.

county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
                   .agg('size')
                   .sort_values(ascending=False)
                   .reset_index(name='count'))

means = county_weights_.mean()
stds = county_weights_.stddev()

fig, ax = plt.subplots(figsize=(20, 5))

for idx, row in county_counts.iterrows():
  mid = means[row.county_code]
  std = stds[row.county_code]
  ax.vlines(idx, mid - std, mid + std, linewidth=3)
  ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)

ax.set(
    xticks=np.arange(len(county_counts)),
    xlim=(-1, len(county_counts)),
    ylabel="County effect",
    title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);

png

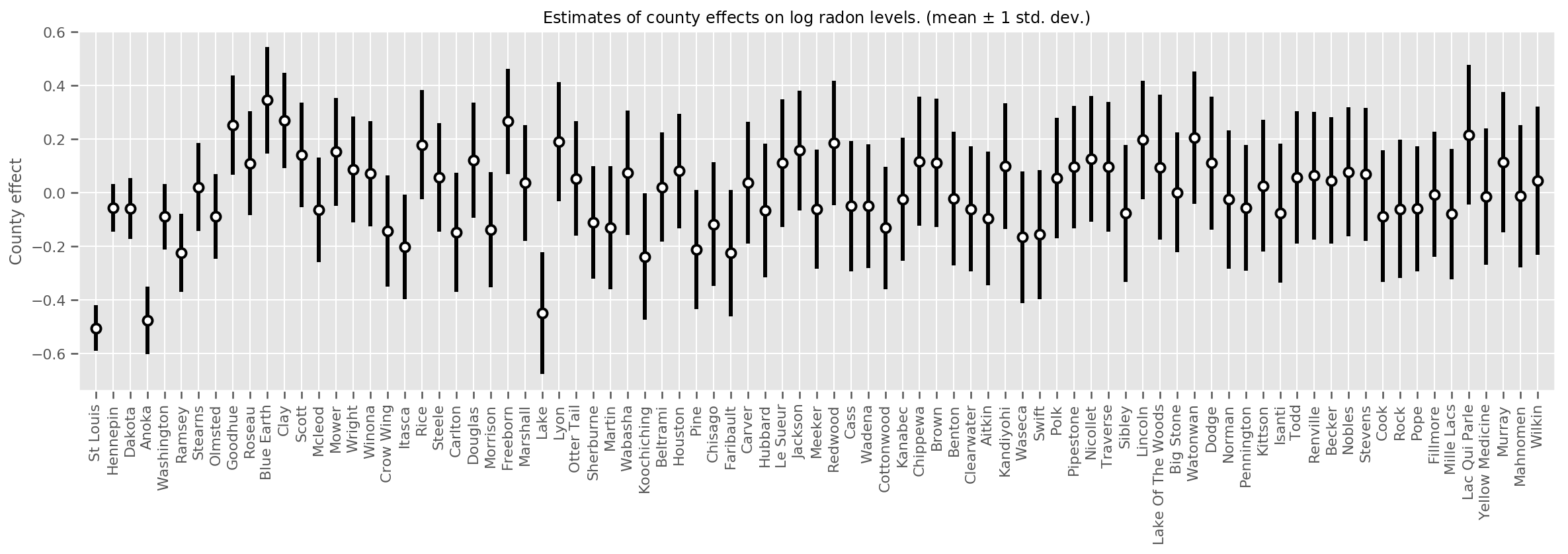
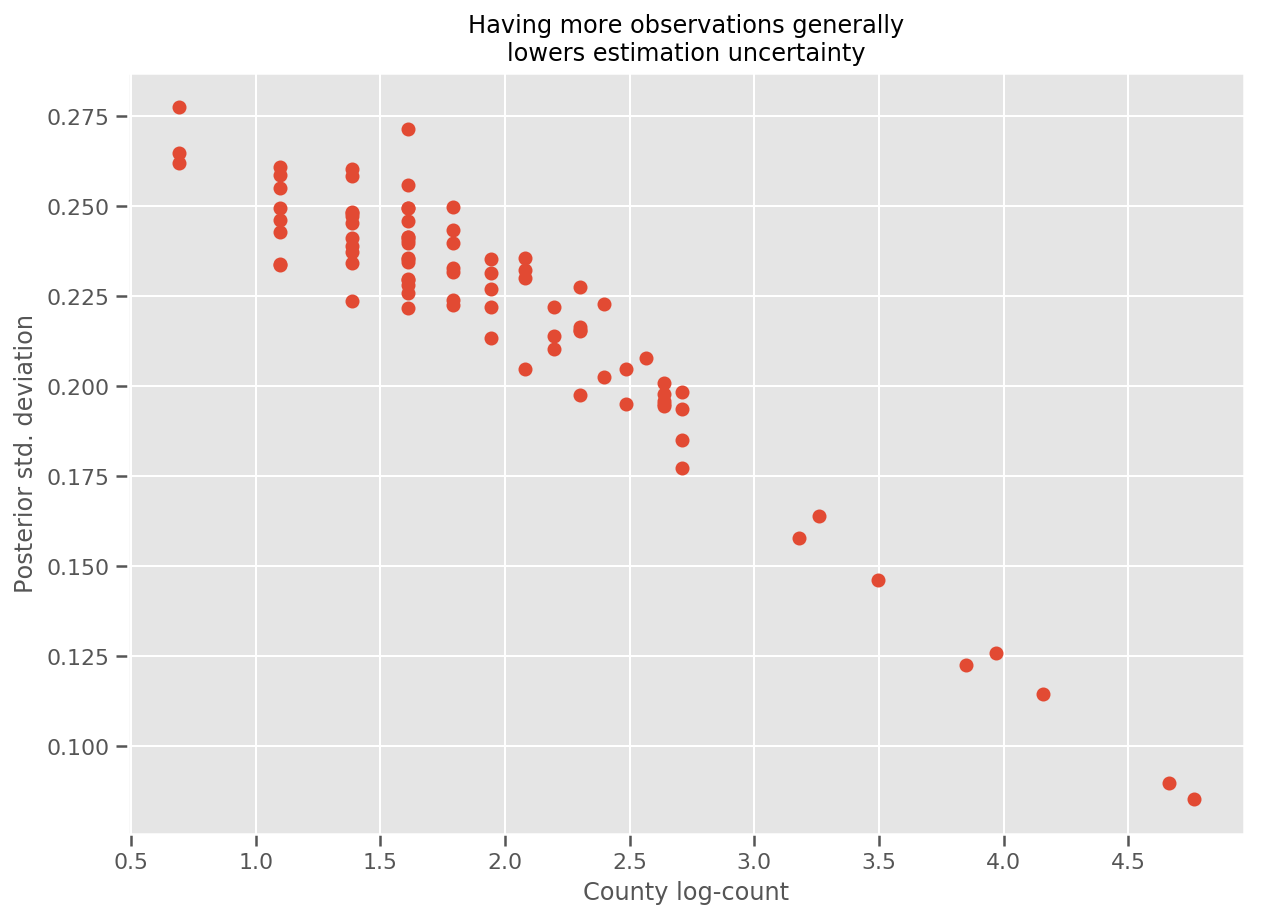
En effet, nous pouvons voir cela plus directement en traçant le nombre logarithmique d'observations par rapport à l'écart type estimé, et voir que la relation est approximativement linéaire.

fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
    ylabel='Posterior std. deviation',
    xlabel='County log-count',
    title='Having more observations generally\nlowers estimation uncertainty'
);

png

Comparé à lme4 dans R

%%shell
exit  # Trick to make this block not execute.

radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)

# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit

# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
#    Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
#  Groups   Name        Std.Dev.
#  county   (Intercept) 0.3282
#  Residual             0.7556
# Number of obs: 919, groups:  county, 85
# Fixed Effects:
# (Intercept)        floor
#       1.462       -0.693

<IPython.core.display.Javascript at 0x7f90b888e9b0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90bce1dfd0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>

Le tableau suivant résume les résultats.

print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
                             floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
                             scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
                   index=['lme4', 'vi']))

intercept   floor     scale
lme4   1.462000 -0.6930  0.328200
vi     1.435284 -0.6702  0.287251

Ce tableau indique les résultats VI sont à ~ 10% des lme4 s. C'est un peu surprenant car :

  • lme4 est basé sur la méthode de Laplace (non VI),
  • aucun effort n'a été fait dans ce colab pour réellement converger,
  • un effort minimal a été fait pour régler les hyperparamètres,
  • aucun effort n'a été fait pour régulariser ou prétraiter les données (par exemple, les caractéristiques du centre, etc.).

Conclusion

Dans cette collaboration, nous avons décrit les modèles linéaires généralisés à effets mixtes et montré comment utiliser l'inférence variationnelle pour les ajuster à l'aide de la probabilité TensorFlow. Bien que le problème du jouet n'ait eu que quelques centaines d'échantillons d'apprentissage, les techniques utilisées ici sont identiques à ce qui est nécessaire à grande échelle.