 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
Un modelo lineal de efectos mixtos es un enfoque simple para modelar relaciones lineales estructuradas (Harville, 1997; Laird y Ware, 1982). Cada punto de datos consta de entradas de diversos tipos, categorizadas en grupos, y una salida de valor real. Un modelo de efectos mixtos lineal es un modelo jerárquico: comparte fuerza estadística entre los grupos a fin de mejorar inferencias sobre cualquier punto de datos individual.
En este instructivo, demostramos modelos lineales de efectos mixtos con un ejemplo del mundo real en TensorFlow Probability. Usaremos el JointDistributionCoroutine y la cadena de Markov Monte Carlo ( tfp.mcmc módulos).
Dependencias y requisitos previos
Importación y configuraciones
import csv
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
dtype = tf.float64
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
plt.style.use('ggplot')
¡Haz las cosas rápido!
Antes de sumergirnos, asegurémonos de que estamos usando una GPU para esta demostración.
Para hacer esto, seleccione "Tiempo de ejecución" -> "Cambiar tipo de tiempo de ejecución" -> "Acelerador de hardware" -> "GPU".
El siguiente fragmento verificará que tenemos acceso a una GPU.
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
SUCCESS: Found GPU: /device:GPU:0
Datos
Utilizamos las InstEval conjunto de datos de la popular lme4 paquete en R (Bates et al., 2015). Es un conjunto de datos de cursos y sus calificaciones de evaluación. Cada curso incluye metadatos, como students , instructors y departments , y la variable de respuesta de interés es la calificación de la evaluación.
def load_insteval():
"""Loads the InstEval data set.
It contains 73,421 university lecture evaluations by students at ETH
Zurich with a total of 2,972 students, 2,160 professors and
lecturers, and several student, lecture, and lecturer attributes.
Implementation is built from the `observations` Python package.
Returns:
Tuple of np.ndarray `x_train` with 73,421 rows and 7 columns and
dictionary `metadata` of column headers (feature names).
"""
url = ('https://raw.github.com/vincentarelbundock/Rdatasets/master/csv/'
'lme4/InstEval.csv')
with requests.Session() as s:
download = s.get(url)
f = download.content.decode().splitlines()
iterator = csv.reader(f)
columns = next(iterator)[1:]
x_train = np.array([row[1:] for row in iterator], dtype=np.int)
metadata = {'columns': columns}
return x_train, metadata
Cargamos y preprocesamos el conjunto de datos. Retenemos el 20% de los datos para que podamos evaluar nuestro modelo ajustado en puntos de datos invisibles. A continuación, visualizamos las primeras filas.
data, metadata = load_insteval()
data = pd.DataFrame(data, columns=metadata['columns'])
data = data.rename(columns={'s': 'students',
'd': 'instructors',
'dept': 'departments',
'y': 'ratings'})
data['students'] -= 1 # start index by 0
# Remap categories to start from 0 and end at max(category).
data['instructors'] = data['instructors'].astype('category').cat.codes
data['departments'] = data['departments'].astype('category').cat.codes
train = data.sample(frac=0.8)
test = data.drop(train.index)
train.head()
Hemos creado el conjunto de datos en términos de una features Diccionario de insumos y una labels de salida correspondiente a las calificaciones. Cada característica está codificada como un número entero y cada etiqueta (calificación de evaluación) está codificada como un número de punto flotante.
get_value = lambda dataframe, key, dtype: dataframe[key].values.astype(dtype)
features_train = {
k: get_value(train, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_train = get_value(train, key='ratings', dtype=np.float32)
features_test = {k: get_value(test, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_test = get_value(test, key='ratings', dtype=np.float32)
num_students = max(features_train['students']) + 1
num_instructors = max(features_train['instructors']) + 1
num_departments = max(features_train['departments']) + 1
num_observations = train.shape[0]
print("Number of students:", num_students)
print("Number of instructors:", num_instructors)
print("Number of departments:", num_departments)
print("Number of observations:", num_observations)
Number of students: 2972 Number of instructors: 1128 Number of departments: 14 Number of observations: 58737
Modelo
Un modelo lineal típico asume independencia, donde cualquier par de puntos de datos tiene una relación lineal constante. En el InstEval conjunto de datos, surgen observaciones en grupos, cada uno de los cuales pueden tener diferentes pendientes e intersecciones. Los modelos lineales de efectos mixtos, también conocidos como modelos lineales jerárquicos o modelos lineales multinivel, capturan este fenómeno (Gelman & Hill, 2006).
Ejemplos de este fenómeno incluyen:
- Estudiantes. Las observaciones de un estudiante no son independientes: algunos estudiantes pueden dar sistemáticamente calificaciones bajas (o altas) en las conferencias.
- Instructores. Las observaciones de un instructor no son independientes: esperamos que los buenos maestros generalmente tengan buenas calificaciones y los malos maestros generalmente tengan malas calificaciones.
- Departamentos. Las observaciones de un departamento no son independientes: ciertos departamentos generalmente pueden tener material seco o una clasificación más estricta y, por lo tanto, recibir una calificación más baja que otros.
Para captar esto, recordemos que para un conjunto de datos de \(N\times D\) cuenta \(\mathbf{X}\) y \(N\) etiquetas \(\mathbf{y}\), postula el modelo de regresión lineal
\[ \begin{equation*} \mathbf{y} = \mathbf{X}\beta + \alpha + \epsilon, \end{equation*} \]
donde hay un vector pendiente \(\beta\in\mathbb{R}^D\), interceptar \(\alpha\in\mathbb{R}\), y ruido aleatorio \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). Decimos que \(\beta\) y \(\alpha\) son "efectos fijos": son efectos se mantienen constantes en toda la población de puntos de datos \((x, y)\). Una formulación equivalente de la ecuación como una probabilidad es \(\mathbf{y} \sim \text{Normal}(\mathbf{X}\beta + \alpha, \mathbf{I})\). Esta probabilidad se maximiza durante la inferencia con el fin de encontrar las estimaciones puntuales de \(\beta\) y \(\alpha\) que se ajustan a los datos.
Un modelo lineal de efectos mixtos extiende la regresión lineal como
\[ \begin{align*} \eta &\sim \text{Normal}(\mathbf{0}, \sigma^2 \mathbf{I}), \\ \mathbf{y} &= \mathbf{X}\beta + \mathbf{Z}\eta + \alpha + \epsilon. \end{align*} \]
donde todavía hay un vector pendiente \(\beta\in\mathbb{R}^P\), interceptar \(\alpha\in\mathbb{R}\), y ruido aleatorio \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). Además, hay un término \(\mathbf{Z}\eta\), donde \(\mathbf{Z}\) es una matriz de características y \(\eta\in\mathbb{R}^Q\) es un vector de pistas aleatorias; \(\eta\) se distribuye normalmente con parámetro componente de varianza \(\sigma^2\). \(\mathbf{Z}\) está formada mediante la partición del original \(N\times D\) características de la matriz en términos de un nuevo \(N\times P\) matriz \(\mathbf{X}\) y \(N\times Q\) matriz \(\mathbf{Z}\), donde \(P + Q=D\): esta partición nos permite modelar las características por separado utilizando el efectos fijos \(\beta\) y la variable latente \(\eta\) respectivamente.
Decimos las variables latentes \(\eta\) son "efectos aleatorios": son efectos que varían en toda la población (aunque pueden ser constante a través de las subpoblaciones). En particular, debido a que los efectos aleatorios \(\eta\) tienen media 0, la media de la etiqueta de datos es capturado por \(\mathbf{X}\beta + \alpha\). Los efectos aleatorios de componentes \(\mathbf{Z}\eta\) variaciones capturas en los datos: por ejemplo, "instructor # 54 tiene una clasificación de 1,4 puntos más alta que la media."
En este tutorial, postulamos los siguientes efectos:
- Los efectos fijos:
service.servicees una covariable binario correspondiente a si el curso pertenece al departamento principal del instructor. No importa la cantidad de datos adicional que recogemos, sólo puede tomar valores \(0\) y \(1\). - Los efectos aleatorios:
students,instructorsydepartments. Dadas más observaciones de la población de calificaciones de evaluación de cursos, es posible que estemos buscando nuevos estudiantes, maestros o departamentos.
En la sintaxis del paquete lme4 de R (Bates et al., 2015), el modelo se puede resumir como
ratings ~ service + (1|students) + (1|instructors) + (1|departments) + 1
donde x denota un efecto fijo, (1|x) denota un efecto al azar para x , y 1 indica un término de intersección.
Implementamos este modelo a continuación como una distribución conjunta. Para tener un mejor soporte para el seguimiento de parámetros (por ejemplo, queremos seguir hasta el tf.Variable en model.trainable_variables ), que aplicar la plantilla modelo como tf.Module .
class LinearMixedEffectModel(tf.Module):
def __init__(self):
# Set up fixed effects and other parameters.
# These are free parameters to be optimized in E-steps
self._intercept = tf.Variable(0., name="intercept") # alpha in eq
self._effect_service = tf.Variable(0., name="effect_service") # beta in eq
self._stddev_students = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_students") # sigma in eq
self._stddev_instructors = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_instructors") # sigma in eq
self._stddev_departments = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_departments") # sigma in eq
def __call__(self, features):
model = tfd.JointDistributionSequential([
# Set up random effects.
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_students),
scale_identity_multiplier=self._stddev_students),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_instructors),
scale_identity_multiplier=self._stddev_instructors),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_departments),
scale_identity_multiplier=self._stddev_departments),
# This is the likelihood for the observed.
lambda effect_departments, effect_instructors, effect_students: tfd.Independent(
tfd.Normal(
loc=(self._effect_service * features["service"] +
tf.gather(effect_students, features["students"], axis=-1) +
tf.gather(effect_instructors, features["instructors"], axis=-1) +
tf.gather(effect_departments, features["departments"], axis=-1) +
self._intercept),
scale=1.),
reinterpreted_batch_ndims=1)
])
# To enable tracking of the trainable variables via the created distribution,
# we attach a reference to `self`. Since all TFP objects sub-class
# `tf.Module`, this means that the following is possible:
# LinearMixedEffectModel()(features_train).trainable_variables
# ==> tuple of all tf.Variables created by LinearMixedEffectModel.
model._to_track = self
return model
lmm_jointdist = LinearMixedEffectModel()
# Conditioned on feature/predictors from the training data
lmm_train = lmm_jointdist(features_train)
lmm_train.trainable_variables
(<tf.Variable 'stddev_students:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_instructors:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_departments:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'effect_service:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'intercept:0' shape=() dtype=float32, numpy=0.0>)
Como programa gráfico probabilístico, también podemos visualizar la estructura del modelo en términos de su gráfico computacional. Este gráfico codifica el flujo de datos a través de las variables aleatorias en el programa, haciendo explícitas sus relaciones en términos de un modelo gráfico (Jordan, 2003).
Como herramienta estadística, podemos fijarnos en el gráfico con el fin de ver mejor, por ejemplo, que intercept y effect_service son condicionalmente dependientes dados ratings ; esto puede ser más difícil de ver en el código fuente si el programa está escrito con clases, referencias cruzadas entre módulos y / o subrutinas. Como una herramienta computacional, también podemos notar variables latentes desembocan en el ratings variables a través de tf.gather ops. Esto puede ser un cuello de botella en ciertos aceleradores de hardware si la indexación Tensor s es caro; visualizar el gráfico hace que esto sea evidente.
lmm_train.resolve_graph()
(('effect_students', ()),
('effect_instructors', ()),
('effect_departments', ()),
('x', ('effect_departments', 'effect_instructors', 'effect_students')))
Estimación de parámetros
Teniendo en cuenta los datos, el objetivo de la inferencia es para el ajuste del modelo de efectos fijos pendiente \(\beta\), interceptar \(\alpha\), y la varianza parámetro componente \(\sigma^2\). El principio de máxima verosimilitud formaliza esta tarea como
\[ \max_{\beta, \alpha, \sigma}~\log p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}; \beta, \alpha, \sigma) = \max_{\beta, \alpha, \sigma}~\log \int p(\eta; \sigma) ~p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}, \eta; \beta, \alpha)~d\eta. \]
En este tutorial, usamos el algoritmo Monte Carlo EM para maximizar esta densidad marginal (Dempster et al., 1977; Wei y Tanner, 1990). Realizamos la cadena de Markov Monte Carlo para calcular la expectativa de la verosimilitud condicional con respecto a la efectos aleatorios ("E-step"), y realizamos un descenso de gradiente para maximizar la expectativa con respecto a los parámetros ("M-step"):
Para el paso E, configuramos Hamiltonian Monte Carlo (HMC). Toma un estado actual (los efectos de estudiante, instructor y departamento) y devuelve un nuevo estado. Asignamos el nuevo estado a las variables de TensorFlow, que denotarán el estado de la cadena HMC.
Para el paso M, usamos la muestra posterior de HMC para calcular una estimación insesgada de la probabilidad marginal hasta una constante. Luego aplicamos su gradiente con respecto a los parámetros de interés. Esto produce un paso descendente estocástico sin sesgo en la probabilidad marginal. Lo implementamos con el optimizador Adam TensorFlow y minimizamos lo negativo del marginal.
target_log_prob_fn = lambda *x: lmm_train.log_prob(x + (labels_train,))
trainable_variables = lmm_train.trainable_variables
current_state = lmm_train.sample()[:-1]
# For debugging
target_log_prob_fn(*current_state)
<tf.Tensor: shape=(), dtype=float32, numpy=-528062.5>
# Set up E-step (MCMC).
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.015,
num_leapfrog_steps=3)
kernel_results = hmc.bootstrap_results(current_state)
@tf.function(autograph=False, jit_compile=True)
def one_e_step(current_state, kernel_results):
next_state, next_kernel_results = hmc.one_step(
current_state=current_state,
previous_kernel_results=kernel_results)
return next_state, next_kernel_results
optimizer = tf.optimizers.Adam(learning_rate=.01)
# Set up M-step (gradient descent).
@tf.function(autograph=False, jit_compile=True)
def one_m_step(current_state):
with tf.GradientTape() as tape:
loss = -target_log_prob_fn(*current_state)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
Realizamos una etapa de calentamiento, que ejecuta una cadena MCMC durante varias iteraciones para que el entrenamiento se pueda inicializar dentro de la masa de probabilidad del posterior. Luego ejecutamos un ciclo de entrenamiento. Ejecuta conjuntamente los pasos E y M y registra los valores durante el entrenamiento.
num_warmup_iters = 1000
num_iters = 1500
num_accepted = 0
effect_students_samples = np.zeros([num_iters, num_students])
effect_instructors_samples = np.zeros([num_iters, num_instructors])
effect_departments_samples = np.zeros([num_iters, num_departments])
loss_history = np.zeros([num_iters])
# Run warm-up stage.
for t in range(num_warmup_iters):
current_state, kernel_results = one_e_step(current_state, kernel_results)
num_accepted += kernel_results.is_accepted.numpy()
if t % 500 == 0 or t == num_warmup_iters - 1:
print("Warm-Up Iteration: {:>3} Acceptance Rate: {:.3f}".format(
t, num_accepted / (t + 1)))
num_accepted = 0 # reset acceptance rate counter
# Run training.
for t in range(num_iters):
# run 5 MCMC iterations before every joint EM update
for _ in range(5):
current_state, kernel_results = one_e_step(current_state, kernel_results)
loss = one_m_step(current_state)
effect_students_samples[t, :] = current_state[0].numpy()
effect_instructors_samples[t, :] = current_state[1].numpy()
effect_departments_samples[t, :] = current_state[2].numpy()
num_accepted += kernel_results.is_accepted.numpy()
loss_history[t] = loss.numpy()
if t % 500 == 0 or t == num_iters - 1:
print("Iteration: {:>4} Acceptance Rate: {:.3f} Loss: {:.3f}".format(
t, num_accepted / (t + 1), loss_history[t]))
Warm-Up Iteration: 0 Acceptance Rate: 1.000 Warm-Up Iteration: 500 Acceptance Rate: 0.754 Warm-Up Iteration: 999 Acceptance Rate: 0.707 Iteration: 0 Acceptance Rate: 1.000 Loss: 98220.266 Iteration: 500 Acceptance Rate: 0.703 Loss: 96003.969 Iteration: 1000 Acceptance Rate: 0.678 Loss: 95958.609 Iteration: 1499 Acceptance Rate: 0.685 Loss: 95921.891
También puede escribir el calentamiento de bucle en un tf.while_loop , y el paso de la formación en un tf.scan o tf.while_loop para la inferencia aún más rápido. Por ejemplo:
@tf.function(autograph=False, jit_compile=True)
def run_k_e_steps(k, current_state, kernel_results):
_, next_state, next_kernel_results = tf.while_loop(
cond=lambda i, state, pkr: i < k,
body=lambda i, state, pkr: (i+1, *one_e_step(state, pkr)),
loop_vars=(tf.constant(0), current_state, kernel_results)
)
return next_state, next_kernel_results
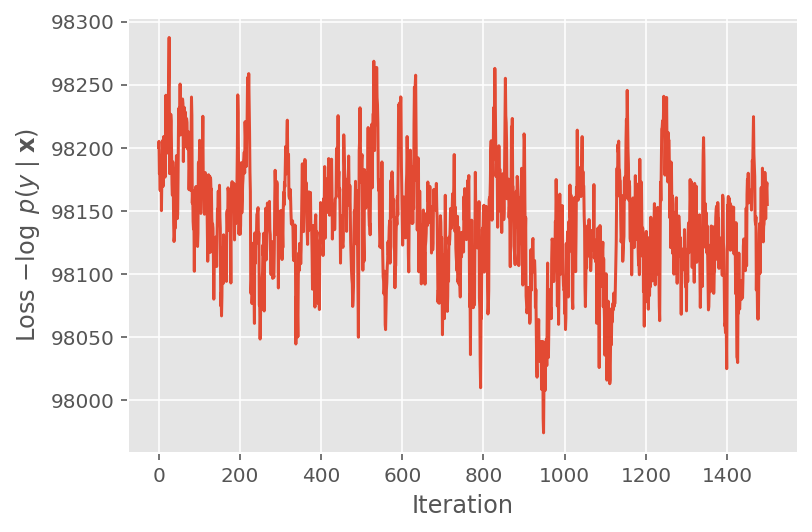
Arriba, no ejecutamos el algoritmo hasta que se detectó un umbral de convergencia. Para comprobar si el entrenamiento fue sensato, verificamos que la función de pérdida de hecho tiende a converger durante las iteraciones de entrenamiento.
plt.plot(loss_history)
plt.ylabel(r'Loss $-\log$ $p(y\mid\mathbf{x})$')
plt.xlabel('Iteration')
plt.show()
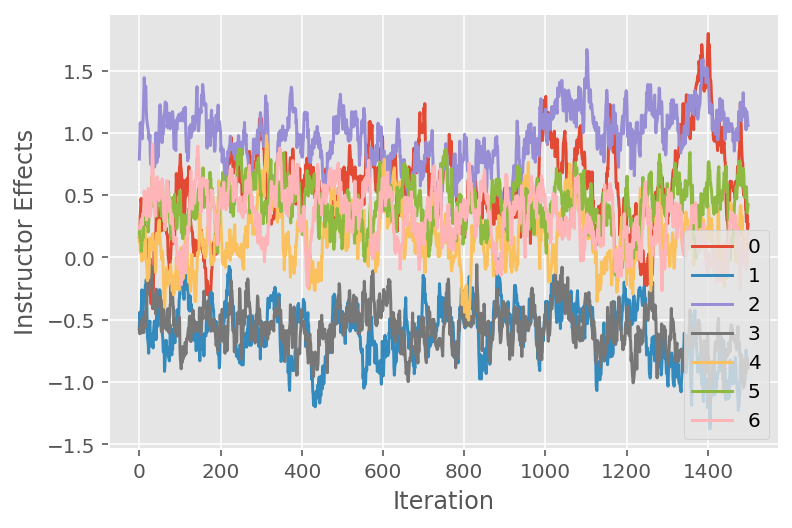
También usamos un diagrama de seguimiento, que muestra la trayectoria del algoritmo de Monte Carlo de la cadena de Markov a través de dimensiones latentes específicas. A continuación, vemos que los efectos específicos del instructor se alejan de manera significativa de su estado inicial y exploran el espacio de estados. El diagrama de seguimiento también indica que los efectos difieren entre los instructores, pero con un comportamiento de mezcla similar.
for i in range(7):
plt.plot(effect_instructors_samples[:, i])
plt.legend([i for i in range(7)], loc='lower right')
plt.ylabel('Instructor Effects')
plt.xlabel('Iteration')
plt.show()
Crítica
Arriba, ajustamos el modelo. Ahora buscamos criticar su ajuste utilizando datos, lo que nos permite explorar y comprender mejor el modelo. Una de esas técnicas es un gráfico residual, que traza la diferencia entre las predicciones del modelo y la verdad del terreno para cada punto de datos. Si el modelo fuera correcto, entonces su diferencia debería ser estándar distribuida normalmente; cualquier desviación de este patrón en el gráfico indica un desajuste del modelo.
Construimos la gráfica residual formando primero la distribución predictiva posterior sobre las calificaciones, que reemplaza la distribución anterior sobre los efectos aleatorios con sus datos de entrenamiento dados posteriormente. En particular, ejecutamos el modelo hacia adelante e interceptamos su dependencia de los efectos aleatorios previos con sus medias posteriores inferidas.²
lmm_test = lmm_jointdist(features_test)
[
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
] = [
np.mean(x, axis=0).astype(np.float32) for x in [
effect_students_samples,
effect_instructors_samples,
effect_departments_samples
]
]
# Get the posterior predictive distribution
(*posterior_conditionals, ratings_posterior), _ = lmm_test.sample_distributions(
value=(
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
))
ratings_prediction = ratings_posterior.mean()
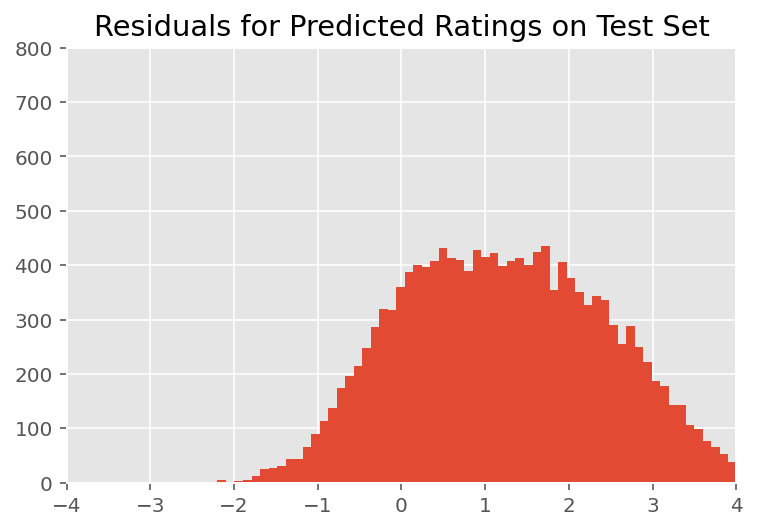
Tras una inspección visual, los residuos se ven algo estándar, distribuidos normalmente. Sin embargo, el ajuste no es perfecto: hay una masa de probabilidad mayor en las colas que una distribución normal, lo que indica que el modelo podría mejorar su ajuste al relajar sus supuestos de normalidad.
En particular, aunque es más común el uso de una distribución normal con las calificaciones de modelo en el InstEval conjunto de datos, un vistazo más de cerca a los datos revela que las calificaciones de evaluación del curso están en valores ordinales de datos de 1 a 5. Esto sugiere que deberíamos estar usando una distribución ordinal, o incluso categórica si tenemos suficientes datos para descartar el orden relativo. Este es un cambio de una línea al modelo anterior; se aplica el mismo código de inferencia.
plt.title("Residuals for Predicted Ratings on Test Set")
plt.xlim(-4, 4)
plt.ylim(0, 800)
plt.hist(ratings_prediction - labels_test, 75)
plt.show()
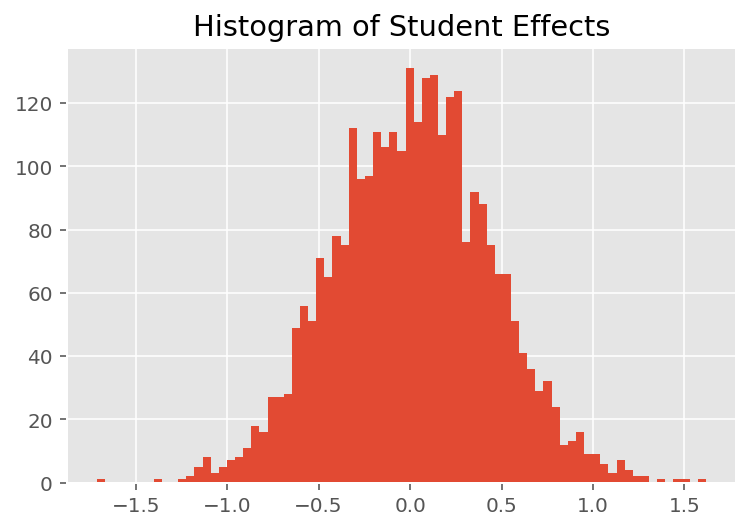
Para explorar cómo el modelo hace predicciones individuales, observamos el histograma de efectos para estudiantes, instructores y departamentos. Esto nos permite comprender cómo los elementos individuales en el vector de características de un punto de datos tienden a influir en el resultado.
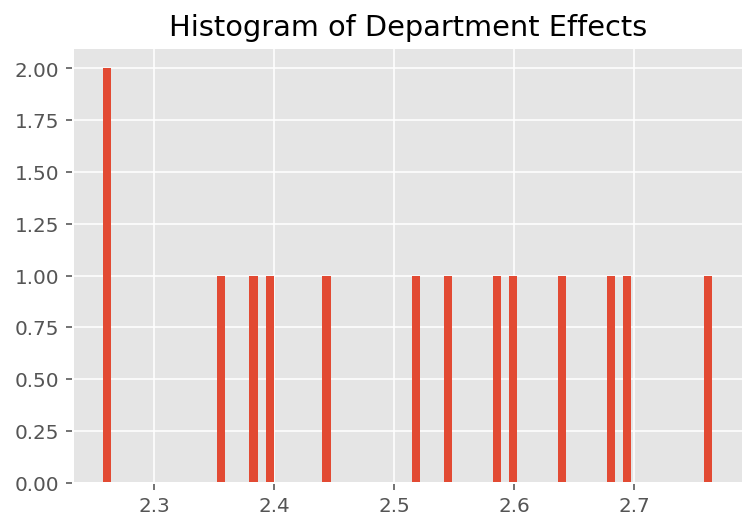
No es sorprendente que veamos a continuación que cada estudiante generalmente tiene poco efecto en la calificación de evaluación de un instructor. Curiosamente, vemos que el departamento al que pertenece un instructor tiene un gran efecto.
plt.title("Histogram of Student Effects")
plt.hist(effect_students_mean, 75)
plt.show()
plt.title("Histogram of Instructor Effects")
plt.hist(effect_instructors_mean, 75)
plt.show()
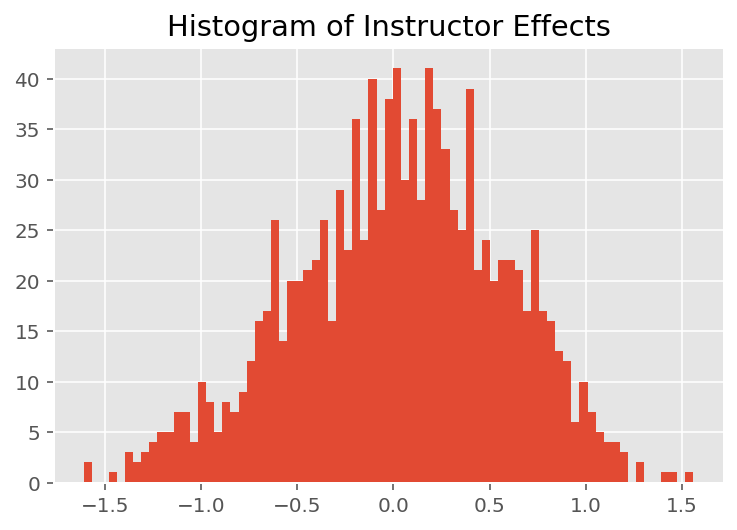
plt.title("Histogram of Department Effects")
plt.hist(effect_departments_mean, 75)
plt.show()
Notas al pie
¹ Los modelos lineales de efectos mixtos son un caso especial en el que podemos calcular analíticamente su densidad marginal. Para los propósitos de este tutorial, demostramos Monte Carlo EM, que se aplica más fácilmente a densidades marginales no analíticas, como si la probabilidad se extendiera para ser Categórica en lugar de Normal.
² Para simplificar, formamos la media de la distribución predictiva utilizando solo una pasada hacia adelante del modelo. Esto se hace condicionando la media posterior y es válido para modelos lineales de efectos mixtos. Sin embargo, esto no es válido en general: la media de la distribución predictiva posterior es típicamente intratable y requiere tomar la media empírica a través de múltiples pases hacia adelante del modelo dadas muestras posteriores.
Expresiones de gratitud
Este tutorial fue escrito originalmente en Edward 1,0 ( fuente ). Agradecemos a todos los colaboradores por escribir y revisar esa versión.
Referencias
Douglas Bates y Martin Machler y Ben Bolker y Steve Walker. Ajuste de modelos lineales de efectos mixtos mediante lme4. Journal of Statistical Software, 67 (1): 1-48, 2015.
Arthur P. Dempster, Nan M. Laird y Donald B. Rubin. Máxima probabilidad de datos incompletos a través del algoritmo EM. Revista de la Real Sociedad de Estadística, Serie B (metodológica), 1-38, 1977.
Andrew Gelman y Jennifer Hill. Análisis de datos mediante regresión y modelos jerárquicos / multinivel. Prensa de la Universidad de Cambridge, 2006.
David A. Harville. Enfoques de máxima verosimilitud para la estimación de componentes de varianza y problemas relacionados. Diario de la Asociación Americana de Estadística, 72 (358): 320-338, 1977.
Michael I. Jordan. Introducción a los modelos gráficos. Informe técnico, 2003.
Nan M. Laird y James Ware. Modelos de efectos aleatorios para datos longitudinales. Biometrics, 963-974, 1982.
Greg Wei y Martin A. Tanner. Una implementación de Monte Carlo del algoritmo EM y los algoritmos de aumento de datos del pobre. Revista de la Asociación Americana de Estadística, 699-704, 1990.
