 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Neste notebook, exploraremos as distribuições do TensorFlow (abreviatura de TFD). O objetivo deste bloco de notas é fazer com que você suba suavemente na curva de aprendizado, incluindo a compreensão do manuseio das formas tensoras do TFD. Este caderno tenta apresentar exemplos anteriores ao invés de conceitos abstratos. Apresentaremos maneiras fáceis canônicas de fazer as coisas primeiro e salvar a visão abstrata mais geral até o final. Se você é do tipo que prefere um tutorial mais abstrato e de estilo de referência, veja Entendendo TensorFlow Distribuições Shapes . Se você tem dúvidas sobre o material aqui, não hesite em contato (ou se juntar) a lista Probabilidade de discussão TensorFlow . Estamos felizes em ajudar.
Antes de começar, precisamos importar as bibliotecas apropriadas. Nossa biblioteca global é tensorflow_probability . Por convenção, que geralmente se referem à biblioteca distribuições como tfd .
Tensorflow Eager é um ambiente de execução imperativo para TensorFlow. No TensorFlow ansioso, cada operação TF é avaliada imediatamente e produz um resultado. Isso contrasta com o modo "gráfico" padrão do TensorFlow, no qual as operações TF adicionam nós a um gráfico que é executado posteriormente. Todo este caderno foi escrito usando TF Eager, embora nenhum dos conceitos apresentados aqui dependa disso, e TFP pode ser usado em modo gráfico.
import collections
import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions
try:
tf.compat.v1.enable_eager_execution()
except ValueError:
pass
import matplotlib.pyplot as plt
Distribuições Univariadas Básicas
Vamos mergulhar de cabeça e criar uma distribuição normal:
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
Podemos tirar uma amostra dele:
n.sample()
<tf.Tensor: shape=(), dtype=float32, numpy=0.25322816>
Podemos extrair várias amostras:
n.sample(3)
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.4658079, -0.5653636, 0.9314412], dtype=float32)>
Podemos avaliar um log prob:
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
Podemos avaliar múltiplas probabilidades de log:
n.log_prob([0., 2., 4.])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-0.9189385, -2.9189386, -8.918939 ], dtype=float32)>
Temos uma ampla variedade de distribuições. Vamos tentar um Bernoulli:
b = tfd.Bernoulli(probs=0.7)
b
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[] event_shape=[] dtype=int32>
b.sample()
<tf.Tensor: shape=(), dtype=int32, numpy=1>
b.sample(8)
<tf.Tensor: shape=(8,), dtype=int32, numpy=array([1, 0, 0, 0, 1, 0, 1, 0], dtype=int32)>
b.log_prob(1)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.35667497>
b.log_prob([1, 0, 1, 0])
<tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.35667497, -1.2039728 , -0.35667497, -1.2039728 ], dtype=float32)>
Distribuições multivariadas
Vamos criar uma normal multivariada com uma covariância diagonal:
nd = tfd.MultivariateNormalDiag(loc=[0., 10.], scale_diag=[1., 4.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
Comparando isso com a normal univariada que criamos anteriormente, o que é diferente?
tfd.Normal(loc=0., scale=1.)
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
Vemos que o univariada normal tem uma event_shape de () , indicando que é uma distribuição escalar. A multivariada normal tem uma event_shape de 2 , indicando o [espaço evento] básico (https://en.wikipedia.org/wiki/Event_ (probability_theory)) desta distribuição é bidimensional.
A amostragem funciona como antes:
nd.sample()
<tf.Tensor: shape=(2,), dtype=float32, numpy=array([-1.2489667, 15.025171 ], dtype=float32)>
nd.sample(5)
<tf.Tensor: shape=(5, 2), dtype=float32, numpy=
array([[-1.5439653 , 8.9968405 ],
[-0.38730723, 12.448896 ],
[-0.8697963 , 9.330035 ],
[-1.2541095 , 10.268944 ],
[ 2.3475595 , 13.184147 ]], dtype=float32)>
nd.log_prob([0., 10])
<tf.Tensor: shape=(), dtype=float32, numpy=-3.2241714>
Os normais multivariados não têm, em geral, covariância diagonal. TFD oferece várias maneiras de criar normais multivariados, incluindo uma especificação de covariância completa, que usamos aqui.
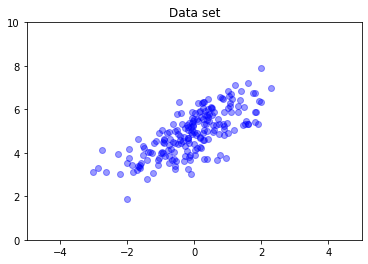
nd = tfd.MultivariateNormalFullCovariance(
loc = [0., 5], covariance_matrix = [[1., .7], [.7, 1.]])
data = nd.sample(200)
plt.scatter(data[:, 0], data[:, 1], color='blue', alpha=0.4)
plt.axis([-5, 5, 0, 10])
plt.title("Data set")
plt.show()
Distribuições Múltiplas
Nossa primeira distribuição Bernoulli representou um lance de uma única moeda justa. Também pode criar um lote de distribuições de Bernoulli independentes, cada um com seus próprios parâmetros, em uma única Distribution objeto:
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
É importante deixar claro o que isso significa. A chamada acima define três distribuições de Bernoulli independentes, que venham a ser contido no mesmo Python Distribution objecto. As três distribuições não podem ser manipuladas individualmente. Nota como o batch_shape é (3,) , indicando um lote de três distribuições, e o event_shape é () , que indica as distribuições individuais têm um espaço para eventos univariada.
Se chamarmos sample , temos uma amostra de todos os três:
b3.sample()
<tf.Tensor: shape=(3,), dtype=int32, numpy=array([0, 1, 1], dtype=int32)>
b3.sample(6)
<tf.Tensor: shape=(6, 3), dtype=int32, numpy=
array([[1, 0, 1],
[0, 1, 1],
[0, 0, 1],
[0, 0, 1],
[0, 0, 1],
[0, 1, 0]], dtype=int32)>
Se chamamos prob , (este tem a mesma semântica forma como log_prob ; usamos prob com estes pequenos exemplos de Bernoulli para maior clareza, embora log_prob é geralmente preferido em aplicações) que pode passar-se um vector e avaliar a probabilidade de cada moeda obtendo-se que o valor :
b3.prob([1, 1, 0])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.29999998], dtype=float32)>
Por que a API inclui a forma de lote? Semanticamente, pode-se realizar os mesmos cálculos através da criação de uma lista de distribuições e iteração sobre eles com um for loop (pelo menos no modo Ansioso, no modo gráfico TF você precisa de um tf.while loop). No entanto, ter um conjunto (potencialmente grande) de distribuições parametrizadas de forma idêntica é extremamente comum, e o uso de cálculos vetorizados sempre que possível é um ingrediente chave para poder realizar cálculos rápidos usando aceleradores de hardware.
Usando Independent para Agregar Lotes a Eventos
Na seção anterior, nós criamos b3 , uma única Distribution objeto que representava três coin flips. Se chamamos b3.prob em um vector \(v\), a \(i\)'th entrada foi a probabilidade de que o \(i\)th moeda toma o valor \(v[i]\).
Suponha que, em vez disso, queiramos especificar uma distribuição "conjunta" sobre variáveis aleatórias independentes da mesma família subjacente. Este é um objeto diferente matematicamente, em que para esta nova distribuição, prob em um vector \(v\) irá retornar um único valor que representa a probabilidade de que todo o conjunto de moedas corresponde ao vector \(v\).
Como podemos fazer isso? Nós usamos uma distribuição "de ordem superior" chamada Independent , que leva uma distribuição e produz uma nova distribuição com a forma de lote mudou-se para a forma evento:
b3_joint = tfd.Independent(b3, reinterpreted_batch_ndims=1)
b3_joint
<tfp.distributions.Independent 'IndependentBernoulli' batch_shape=[] event_shape=[3] dtype=int32>
Compare a forma para que o original b3 :
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
Como prometido, vemos que que Independent mudou a forma de lote na forma de eventos: b3_joint é uma distribuição única ( batch_shape = () ) ao longo de um espaço evento tridimensional ( event_shape = (3,) ).
Vamos verificar a semântica:
b3_joint.prob([1, 1, 0])
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999998>
Uma maneira alternativa de obter o mesmo resultado seria a probabilidade de computação usando b3 e fazer a redução manualmente através da multiplicação (ou, no caso mais usual, onde as probabilidades de log são usados, soma):
tf.reduce_prod(b3.prob([1, 1, 0]))
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999994>
Indpendent permite ao usuário representam mais explicitamente o conceito desejado. Consideramos isso extremamente útil, embora não seja estritamente necessário.
Curiosidades:
-
b3.sampleeb3_joint.sampletêm diferentes implementações conceptuais, mas saídas indistinguíveis: a diferença entre um lote de distribuições independentes e uma única distribuição criado a partir do lote utilizandoIndependentmostra-se ao calcular probabilites, não no momento da amostragem. -
MultivariateNormalDiagpoderia ser trivialmente implementado usando as escalaresNormaleIndependentdistribuições (não é realmente implementado desta forma, mas poderia ser).
Lotes de distinções multivariadas
Vamos criar um lote de três normais multivariados bidimensionais de covariância total:
nd_batch = tfd.MultivariateNormalFullCovariance(
loc = [[0., 0.], [1., 1.], [2., 2.]],
covariance_matrix = [[[1., .1], [.1, 1.]],
[[1., .3], [.3, 1.]],
[[1., .5], [.5, 1.]]])
nd_batch
<tfp.distributions.MultivariateNormalFullCovariance 'MultivariateNormalFullCovariance' batch_shape=[3] event_shape=[2] dtype=float32>
Vemos batch_shape = (3,) , de forma que há três normais multivariadas independentes, e event_shape = (2,) , de modo que cada multivariada normal é bidimensional. Neste exemplo, as distribuições individuais não possuem elementos independentes.
Amostragem funciona:
nd_batch.sample(4)
<tf.Tensor: shape=(4, 3, 2), dtype=float32, numpy=
array([[[ 0.7367498 , 2.730996 ],
[-0.74080074, -0.36466932],
[ 0.6516018 , 0.9391426 ]],
[[ 1.038303 , 0.12231752],
[-0.94788766, -1.204232 ],
[ 4.059758 , 3.035752 ]],
[[ 0.56903946, -0.06875849],
[-0.35127294, 0.5311631 ],
[ 3.4635801 , 4.565582 ]],
[[-0.15989424, -0.25715637],
[ 0.87479895, 0.97391707],
[ 0.5211419 , 2.32108 ]]], dtype=float32)>
Desde batch_shape = (3,) e event_shape = (2,) , que passar um tensor de forma (3, 2) para log_prob :
nd_batch.log_prob([[0., 0.], [1., 1.], [2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.8328519, -1.7907217, -1.694036 ], dtype=float32)>
Broadcasting, também conhecido como Por que isso é tão confuso?
Abstraindo o que temos feito até agora, todas as distribuições tem uma forma de lote B e uma forma evento E . Let BE ser a concatenação das formas de evento:
- Para as distribuições escalares univariadas
neb,BE = ().. - Para as normais multivariadas bidimensionais
nd.BE = (2). - Para ambos
b3eb3_joint,BE = (3). - Para o lote de normais multivariadas
ndb,BE = (3, 2).
As "regras de avaliação" que usamos até agora são:
- Amostra sem argumento retorna um tensor com forma
BE; amostragem com um escalar n retorna um "n porBE" tensor. -
probelog_probtomar um tensor de formaBEe retornar um resultado de formaB.
A "regra de avaliação" real para prob e log_prob é mais complicado, de uma forma que oferece potência potencial e velocidade, mas também a complexidade e desafios. A regra atual é (essencialmente) que o argumento para log_prob deve ser irradiável contra BE ; quaisquer dimensões "extras" são preservadas na saída.
Vamos explorar as implicações. Para o normal, univariada n , BE = () , de modo log_prob espera um escalar. Se passar log_prob um tensor com a forma não-vazia, aqueles mostrados como dimensões de lote na produção:
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
n.log_prob([0.])
<tf.Tensor: shape=(1,), dtype=float32, numpy=array([-0.9189385], dtype=float32)>
n.log_prob([[0., 1.], [-1., 2.]])
<tf.Tensor: shape=(2, 2), dtype=float32, numpy=
array([[-0.9189385, -1.4189385],
[-1.4189385, -2.9189386]], dtype=float32)>
Vamos virar à normalidade multivariada bidimensional nd (parâmetros alterados para fins ilustrativos):
nd = tfd.MultivariateNormalDiag(loc=[0., 1.], scale_diag=[1., 1.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
log_prob "espera" uma discussão com forma (2,) , mas vai aceitar qualquer argumento de que as transmissões contra esta forma:
nd.log_prob([0., 0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
Mas podemos passar em "mais" exemplos, e avaliar todo o seu log_prob é ao mesmo tempo:
nd.log_prob([[0., 0.],
[1., 1.],
[2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
Talvez menos atraente, podemos transmitir sobre as dimensões do evento:
nd.log_prob([0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
nd.log_prob([[0.], [1.], [2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
A transmissão dessa forma é uma consequência do nosso design "habilitar a transmissão sempre que possível"; este uso é um tanto controverso e poderia ser removido em uma versão futura do TFP.
Agora, vamos examinar o exemplo das três moedas novamente:
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
Aqui, usando transmissão para representar a probabilidade de que cada moeda dá cara é bastante intuitiva:
b3.prob([1])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.7 ], dtype=float32)>
(Compare isso com b3.prob([1., 1., 1.]) , que teríamos de volta usado onde b3 foi introduzido.)
Agora, suponha que queremos saber, para cada moeda, a probabilidade da moeda dá cara ea probabilidade se trata-se caudas. Podemos nos imaginar tentando:
b3.log_prob([0, 1])
Infelizmente, isso produz um erro com um rastreamento de pilha longo e não muito legível. b3 tem BE = (3) , de modo que deve passar b3.prob irradiável alguma coisa contra (3,) . [0, 1] tem uma forma (2) , para que ele não transmite e cria um erro. Em vez disso, temos que dizer:
b3.prob([[0], [1]])
<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[0.7, 0.5, 0.3],
[0.3, 0.5, 0.7]], dtype=float32)>
Por quê? [[0], [1]] tem forma (2, 1) , de modo que ele transmite contra a forma (3) para fazer uma forma de transmissão (2, 3) .
A transmissão é bastante poderosa: há casos em que permite uma redução de ordem de magnitude na quantidade de memória usada e, muitas vezes, torna o código do usuário mais curto. No entanto, pode ser um desafio programar. Se você chamar log_prob e obter um erro, uma falha de transmissão é quase sempre o problema.
Indo mais longe
Neste tutorial, (esperançosamente) fornecemos uma introdução simples. Algumas dicas para ir mais longe:
-
event_shape,batch_shapeesample_shapepode ser posto arbitrária (neste tutorial são sempre quer escalar ou rank 1). Isso aumenta a potência, mas, novamente, pode levar a desafios de programação, especialmente quando a transmissão está envolvida. Para um mergulho profundo adicional em forma de manipulação, ver os Entendendo TensorFlow Distribuições Shapes . - PTF inclui uma abstracção poderoso conhecido como
Bijectors, que em conjunto comTransformedDistribution, produz uma maneira flexível, de composição para criar facilmente novos distribuições que são transformações inversíveis de distribuição existentes. Vamos tentar escrever um tutorial sobre isso em breve, mas enquanto isso, confira a documentação
