Voir sur TensorFlow.org

Exécuter dans Google Colab

Voir la source sur GitHub

Télécharger le cahier

J'ai écrit ce cahier comme étude de cas pour apprendre la probabilité TensorFlow. Le problème que j'ai choisi de résoudre est d'estimer une matrice de covariance pour des échantillons d'une variable aléatoire gaussienne moyenne 2D 0. Le problème a quelques fonctionnalités intéressantes :

• Si nous utilisons un a priori de Wishart inverse pour la covariance (une approche courante), le problème a une solution analytique, nous pouvons donc vérifier nos résultats.
• Le problème consiste à échantillonner un paramètre contraint, ce qui ajoute une complexité intéressante.
• La solution la plus simple n'est pas la plus rapide, il y a donc un travail d'optimisation à faire.

J'ai décidé d'écrire mes expériences au fur et à mesure. Il m'a fallu un certain temps pour comprendre les subtilités de la TFP, donc ce bloc-notes commence assez simplement, puis évolue progressivement vers des fonctionnalités TFP plus complexes. J'ai rencontré de nombreux problèmes en cours de route et j'ai essayé de capturer à la fois les processus qui m'ont aidé à les identifier et les solutions de contournement que j'ai finalement trouvées. J'ai essayé d'inclure beaucoup de détails (y compris beaucoup de tests à faire des mesures individuelles sont correctes).

Pourquoi apprendre la probabilité TensorFlow ?

J'ai trouvé TensorFlow Probability attrayant pour mon projet pour plusieurs raisons :

• La probabilité TensorFlow vous permet de prototyper le développement de modèles complexes de manière interactive dans un bloc-notes. Vous pouvez diviser votre code en petits morceaux que vous pouvez tester de manière interactive et avec des tests unitaires.
• Une fois que vous êtes prêt à évoluer, vous pouvez profiter de toute l'infrastructure dont nous disposons pour faire fonctionner TensorFlow sur plusieurs processeurs optimisés sur plusieurs machines.
• Enfin, bien que j'aime beaucoup Stan, je trouve qu'il est assez difficile à déboguer. Vous devez écrire tout votre code de modélisation dans un langage autonome qui dispose de très peu d'outils pour vous permettre de fouiller dans votre code, d'inspecter les états intermédiaires, etc.

L'inconvénient est que TensorFlow Probability est beaucoup plus récent que Stan et PyMC3, donc la documentation est un travail en cours, et de nombreuses fonctionnalités doivent encore être construites. Heureusement, j'ai trouvé que la base de TFP était solide et qu'elle est conçue de manière modulaire qui permet d'étendre ses fonctionnalités de manière assez simple. Dans ce cahier, en plus de résoudre l'étude de cas, je montrerai quelques façons d'étendre la PTF.

C'est pour qui

Je suppose que les lecteurs arrivent à ce cahier avec des conditions préalables importantes. Tu devrais:

• Connaître les bases de l'inférence bayésienne. (Si vous ne le faites pas, un premier livre est vraiment sympa statistique Rethinking )
• Avoir une certaine familiarité avec une bibliothèque d'échantillonnage MCMC, par exemple Stan / PyMC3 / BUGS
• Avoir une solide connaissance de NumPy (Une bonne intro est Python pour l' analyse des données )
• Avoir au moins la familiarité de passage avec tensorflow , mais pas nécessairement l' expertise. ( Apprentissage tensorflow est bonne, mais rapide des moyens d'évolution de tensorflow que la plupart des livres sera un peu daté. Stanford CS20 le cours est également bon.)

Premier essai

Voici ma première tentative pour résoudre le problème. Spoiler : ma solution ne fonctionne pas, et il va falloir plusieurs tentatives pour que les choses se passent bien ! Bien que le processus prenne un certain temps, chaque tentative ci-dessous a été utile pour apprendre une nouvelle partie de la PTF.

Une note: TFP n'implémente pas actuellement la distribution de Wishart inverse (nous verrons à la fin comment faire rouler notre propre Wishart inverse), donc à la place, je vais changer le problème en celui d'estimer une matrice de précision à l'aide d'un a priori de Wishart.

import collections
import math
import os
import time

import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

Étape 1 : rassembler les observations

Mes données ici sont toutes synthétiques, donc cela va sembler un peu plus ordonné qu'un exemple du monde réel. Cependant, il n'y a aucune raison pour que vous ne puissiez pas générer vos propres données synthétiques.

Astuce: Une fois que vous avez décidé sur la forme de votre modèle, vous pouvez choisir des valeurs de paramètres et d' utiliser votre modèle choisi pour générer des données synthétiques. En guise de vérification de l'intégrité de votre implémentation, vous pouvez ensuite vérifier que vos estimations incluent les vraies valeurs des paramètres que vous avez choisis. Pour accélérer votre cycle de débogage/test, vous pouvez envisager une version simplifiée de votre modèle (par exemple, utiliser moins de dimensions ou moins d'échantillons).

Astuce: Il est plus facile de travailler avec vos observations sous forme de tableaux numpy. Une chose importante à noter est que NumPy utilise par défaut des float64, tandis que TensorFlow utilise par défaut des float32.

En général, les opérations TensorFlow veulent que tous les arguments aient le même type, et vous devez effectuer un casting de données explicite pour modifier les types. Si vous utilisez des observations float64, vous devrez ajouter de nombreuses opérations de transtypage. NumPy, en revanche, s'occupera de la diffusion automatiquement. Par conséquent, il est beaucoup plus facile de convertir vos données en NumPy float32 que de forcer tensorflow à utiliser float64.

Choisissez des valeurs de paramètres

# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
    np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)

# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))

[[4.  1.8]
 [1.8 1. ]]
eigenvalues:  [4.843075   0.15692513]

Générer des observations synthétiques

Notez que tensorflow Probabilité utilise la convention que la dimension initiale (s) de vos données représentent des indices échantillons, et la dimension finale (s) de vos données représentent la dimensionnalité de vos échantillons.

Nous voulons ici 100 échantillons, dont chacun est un vecteur de longueur 2. Nous allons générer un tableau my_data avec la forme (100, 2). my_data[i, :] est le \(i\)ième échantillon, et il est un vecteur de longueur 2.

(Rappelez - vous de faire my_data avoir le type float32!)

# Set the seed so the results are reproducible.
np.random.seed(123)

# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
    mean=true_mean, cov=true_cov, size=100,
    check_valid='ignore').astype(np.float32)

my_data.shape

(100, 2)

Vérifier la santé mentale des observations

Une source potentielle de bugs est de gâcher vos données synthétiques ! Faisons quelques vérifications simples.

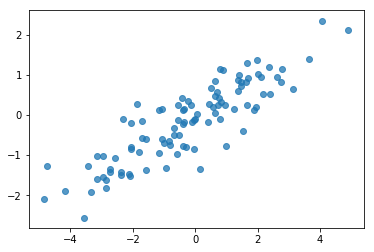
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()

print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)

mean of observations: [-0.24009615 -0.16638893]
true mean: [0. 0.]

print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)

covariance of observations:
 [[3.95307734 1.68718486]
 [1.68718486 0.94910269]]
true covariance:
 [[4.  1.8]
 [1.8 1. ]]

Ok, nos échantillons ont l'air raisonnables. L'étape suivante.

Étape 2 : implémenter la fonction de vraisemblance dans NumPy

La principale chose que nous aurons besoin d'écrire pour effectuer notre échantillonnage MCMC dans TF Probability est une fonction de probabilité de log. En général, il est un peu plus délicat d'écrire TF que NumPy, donc je trouve utile de faire une implémentation initiale dans NumPy. Je vais diviser la fonction de vraisemblance en 2 morceaux, une fonction de vraisemblance de données qui correspond à \(P(data | parameters)\) et une fonction de la probabilité avant correspondant à \(P(parameters)\).

Notez que ces fonctions NumPy n'ont pas besoin d'être super optimisées / vectorisées car le but est juste de générer des valeurs pour les tests. L'exactitude est la considération clé!

Tout d'abord, nous allons implémenter l'élément de vraisemblance du journal de données. C'est assez simple. La seule chose à retenir est que nous allons travailler avec des matrices de précision, nous allons donc paramétrer en conséquence.

def log_lik_data_numpy(precision, data):
  # np.linalg.inv is a really inefficient way to get the covariance matrix, but
  # remember we don't care about speed here
  cov = np.linalg.inv(precision)
  rv = scipy.stats.multivariate_normal(true_mean, cov)
  return np.sum(rv.logpdf(data))

# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)

-280.81822950593767

Nous allons utiliser une Wishart pour la matrice de précision car il y a une solution analytique pour la partie postérieure (voir tableau pratique de Wikipédia de prieurs conjugué ).

La distribution de Wishart a 2 paramètres:

• le nombre de degrés de liberté (marqué \(\nu\) dans Wikipedia)
• une matrice d'échelle (marqué \(V\) dans Wikipedia)

La moyenne pour une distribution Wishart avec des paramètres \(\nu, V\) est \(E[W] = \nu V\)et la variance est \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)

Une intuition utile: Vous pouvez générer un échantillon Wishart en générant \(\nu\) indépendant tire \(x_1 \ldots x_{\nu}\) d'une variable aléatoire normale multivariée moyenne 0 et covariance \(V\) puis former la somme \(W = \sum_{i=1}^{\nu} x_i x_i^T\).

Si vous redimensionnez échantillons Wishart en les divisant par \(\nu\), vous obtenez la matrice de covariance échantillon du \(x_i\). Cette matrice de covariance échantillon doit tendre vers \(V\) comme \(\nu\) augmente. Lorsque \(\nu\) est petite, il y a beaucoup de variation dans la matrice de covariance exemple, celle des petites valeurs de \(\nu\) correspondent aux prieurs plus faibles et les grandes valeurs de \(\nu\) correspondent à prieurs plus forts. Notez que \(\nu\) doit être au moins aussi grande que la dimension de l'espace que vous échantillonnons ou vous allez générer des matrices singulières.

Nous allons utiliser \(\nu = 3\) nous avons donc une faible avant, et nous allons prendre \(V = \frac{1}{\nu} I\) qui va tirer notre estimation de covariance vers l'identité (rappelons que la moyenne est \(\nu V\)).

PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF

def log_lik_prior_numpy(precision):
  rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
  return rv.logpdf(precision)

# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)

-9.103606346649766

La distribution de Wishart est le conjugué avant d'estimation de la matrice de précision d'une normale multivariée avec connue moyenne \(\mu\).

Supposons que les paramètres antérieurs sont Wishart \(\nu, V\) et que nous avons \(n\) observations de notre normale à plusieurs variables, \(x_1, \ldots, x_n\). Les paramètres postérieurs sont \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\).

n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
                       (v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))

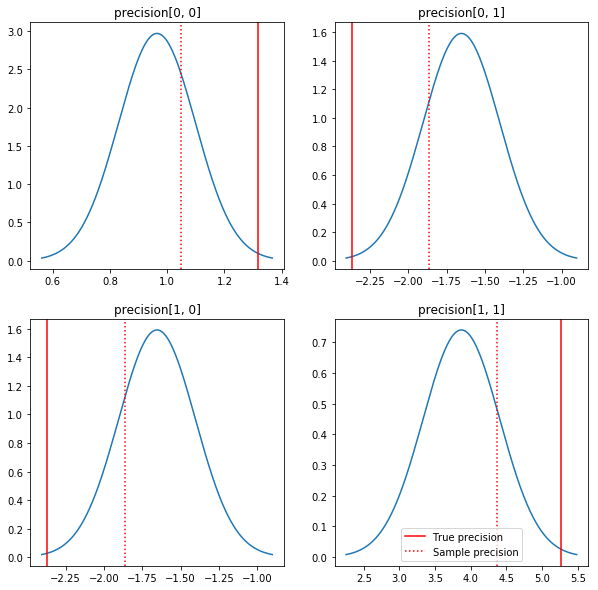
Un tracé rapide des postérieurs et des vraies valeurs. Notez que les postérieurs sont proches des postérieurs de l'échantillon mais sont un peu rétrécis vers l'identité. Notez également que les vraies valeurs sont assez éloignées du mode postérieur - probablement parce que prior ne correspond pas très bien à nos données. Dans un vrai problème que nous ferions probablement mieux avec quelque chose comme une échelle inverse Wishart avant la covariance (voir, par exemple, Andrew Gelman le commentaire sur le sujet), mais nous ne serions pas une belle postérieure analytique.

sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
  for j in range(2):
    ax = axes[i, j]
    loc = posterior_mean[i, j]
    scale = posterior_sd[i, j]
    xmin = loc - 3.0 * scale
    xmax = loc + 3.0 * scale
    x = np.linspace(xmin, xmax, 1000)
    y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
    ax.plot(x, y)
    ax.axvline(true_precision[i, j], color='red', label='True precision')
    ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
    ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()

Étape 3 : implémenter la fonction de vraisemblance dans TensorFlow

Spoiler : Notre première tentative ne fonctionnera pas ; nous expliquerons pourquoi ci-dessous.

Conseil: utilisez le mode tensorflow désireux de développer vos fonctions lors de vraisemblance. Le mode Désireuse fait TF se comportent plus comme NumPy - tout exécute immédiatement, de sorte que vous pouvez déboguer de manière interactive au lieu d'avoir à utiliser Session.run() . Voir les notes ici .

Préliminaire : Classes de distribution

TFP possède une collection de classes de distribution que nous utiliserons pour générer nos probabilités de journal. Une chose à noter est que ces classes fonctionnent avec des tenseurs d'échantillons plutôt que de simples échantillons - cela permet la vectorisation et les accélérations associées.

Une distribution peut fonctionner avec un tenseur d'échantillons de 2 manières différentes. Il est plus simple d'illustrer ces 2 manières avec un exemple concret impliquant une distribution avec un seul paramètre scalaire. Je vais utiliser la Poisson distribution, ce qui a un rate paramètre.

• Si nous créons un Poisson avec une valeur unique pour le rate paramètre, un appel à son sample() méthode retourne une valeur unique. Cette valeur est appelée un event , et dans ce cas , les événements sont tous scalaires.
• Si nous créons un Poisson avec un tenseur de valeurs pour le rate paramètre, un appel à son sample() méthode retourne maintenant plusieurs valeurs, une pour chaque valeur du tenseur de taux. L'objet agit comme une collection de Poissons indépendants, chacun avec son propre taux, et chacune des valeurs retournées par un appel à l' sample() correspond à une de ces Poissons. Cette collection d'événements indépendants mais non équidistribuées est appelé un batch .
• L' sample() méthode prend un sample_shape paramètre par défaut pour un tuple vide. Le passage d' une valeur non vide pour sample_shape résultats de l'échantillon reviennent plusieurs lots. Cette collection de lots est appelé un sample .

Une distribution de log_prob() la méthode consomme les données d'une manière qui est parallèle à la façon dont l' sample() génère. log_prob() retourne probabilités pour les échantillons, soit pour plusieurs lots, indépendants des événements.

• Si nous avons notre objet de Poisson qui a été créé avec un scalaire rate , chaque lot est un scalaire, et si on passe dans un tenseur d'échantillons, nous allons sortir un tenseur de la même taille des probabilités log.
• Si nous avons notre objet de Poisson qui a été créé avec un tenseur de forme T des rate valeurs, chaque lot est un tenseur de forme T . Si on passe dans un tenseur d'échantillons de forme D, T, on obtient un tenseur de log probabilités de forme D, T.

Voici quelques exemples qui illustrent ces cas. Voir ce portable pour un tutoriel plus détaillé sur les événements, les lots et les formes.

# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))

# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters.  Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))

print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())

iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385]
draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]

Probabilité du journal de données

Tout d'abord, nous allons implémenter la fonction de vraisemblance du journal de données.

VALIDATE_ARGS = True
ALLOW_NAN_STATS = False

Une différence clé par rapport au cas NumPy est que notre fonction de vraisemblance TensorFlow devra gérer des vecteurs de matrices de précision plutôt que de simples matrices. Des vecteurs de paramètres seront utilisés lorsque nous échantillonnerons à partir de plusieurs chaînes.

Nous allons créer un objet de distribution qui fonctionne avec un lot de matrices de précision (c'est-à-dire une matrice par chaîne).

Lors du calcul des probabilités de journal de nos données, nous aurons besoin que nos données soient répliquées de la même manière que nos paramètres afin qu'il y ait une copie par variable de lot. La forme de nos données répliquées devra être la suivante :

[sample shape, batch shape, event shape]

Dans notre cas, la forme de l'événement est 2 (puisque nous travaillons avec des gaussiennes 2D). La forme de l'échantillon est 100, puisque nous avons 100 échantillons. La forme du lot sera simplement le nombre de matrices de précision avec lesquelles nous travaillons. Il est inutile de répliquer les données à chaque fois que nous appelons la fonction de vraisemblance, nous allons donc répliquer les données à l'avance et transmettre la version répliquée.

Notez que ceci est une mise en œuvre inefficace: MultivariateNormalFullCovariance est cher par rapport à des solutions de rechange que nous allons parler dans la section d'optimisation à la fin.

def log_lik_data(precisions, replicated_data):
  n = tf.shape(precisions)[0]  # number of precision matrices
  # We're estimating a precision matrix; we have to invert to get log
  # probabilities.  Cholesky inversion should be relatively efficient,
  # but as we'll see later, it's even better if we can avoid doing the Cholesky
  # decomposition altogether.
  precisions_cholesky = tf.linalg.cholesky(precisions)
  covariances = tf.linalg.cholesky_solve(
      precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
  rv_data = tfd.MultivariateNormalFullCovariance(
      loc=tf.zeros([n, 2]),
      covariance_matrix=covariances,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)

  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data).  We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)

(100, 2, 2)

Astuce: Une chose que j'ai trouvé extrêmement utile est écrit peu vérifie santé mentale de mes fonctions de tensorflow. Il est vraiment facile de gâcher la vectorisation dans TF, donc disposer des fonctions NumPy plus simples est un excellent moyen de vérifier la sortie TF. Considérez-les comme de petits tests unitaires.

# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.8182

Log de vraisemblance antérieure

Le préalable est plus facile car nous n'avons pas à nous soucier de la réplication des données.

@tf.function(autograph=False)
def log_lik_prior(precisions):
  rv_precision = tfd.WishartTriL(
      df=PRIOR_DF,
      scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)
  return rv_precision.log_prob(precisions)

# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]))
  print('tensorflow:', lik_tf[i])

0
numpy: -2.2351873809649625
tensorflow: -2.2351875
1
numpy: -9.103606346649766
tensorflow: -9.103608

Construire la fonction de probabilité logarithmique conjointe

La fonction de vraisemblance du journal de données ci-dessus dépend de nos observations, mais l'échantillonneur ne les aura pas. Nous pouvons nous débarrasser de la dépendance sans utiliser de variable globale en utilisant une [closure](https://en.wikipedia.org/wiki/Closure_(computer_programming). Les fermetures impliquent une fonction externe qui crée un environnement contenant les variables nécessaires à un fonction intérieure.

def get_log_lik(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik(precision):
    return log_lik_data(precision, replicated_data) + log_lik_prior(precision)

  return _log_lik

Étape 4 : Échantillon

Ok, il est temps de goûter ! Pour simplifier les choses, nous utiliserons simplement 1 chaîne et nous utiliserons la matrice d'identité comme point de départ. Nous ferons les choses plus soigneusement plus tard.

Encore une fois, cela ne fonctionnera pas - nous aurons une exception.

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  init_precision = tf.expand_dims(tf.eye(2), axis=0)

  # Use expand_dims because we want to pass in a tensor of starting values
  log_lik_fn = get_log_lik(my_data, n_chains=1)

  # we'll just do a few steps here
  num_results = 10
  num_burnin_steps = 10
  states = tfp.mcmc.sample_chain(
     num_results=num_results,
     num_burnin_steps=num_burnin_steps,
     current_state=[
         init_precision,
     ],
     kernel=tfp.mcmc.HamiltonianMonteCarlo(
         target_log_prob_fn=log_lik_fn,
         step_size=0.1,
         num_leapfrog_steps=3),
     trace_fn=None,
     seed=123)
  return states

try:
  states = sample()
except Exception as e:
  # shorten the giant stack trace
  lines = str(e).split('\n')
  print('\n'.join(lines[:5]+['...']+lines[-3:]))

Cholesky decomposition was not successful. The input might not be valid.
     [[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]

Function call stack:
sample
...
Function call stack:
sample

Identifier le problème

InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. Ce n'est pas super utile. Voyons si nous pouvons en savoir plus sur ce qui s'est passé.

• Nous imprimerons les paramètres de chaque étape afin que nous puissions voir la valeur pour laquelle les choses échouent
• Nous allons ajouter quelques assertions pour se prémunir contre des problèmes spécifiques.

Les assertions sont délicates car ce sont des opérations TensorFlow, et nous devons veiller à ce qu'elles soient exécutées et ne soient pas optimisées en dehors du graphique. Il vaut la peine de lire cet aperçu de débogage tensorflow si vous n'êtes pas familier avec les assertions de TF. Vous pouvez forcer explicitement affirmations à exécuter à l' aide tf.control_dependencies (voir les commentaires dans le code ci - dessous).

Natif de tensorflow Print la fonction a le même comportement que les assertions - c'est une opération, et vous avez besoin de prendre quelques précautions pour assurer qu'il exécute. Print provoque des maux de tête supplémentaires lorsque nous travaillons dans un bloc - notes: sa sortie est envoyé à stderr et stderr ne figure pas dans la cellule. Nous allons utiliser une astuce ici: au lieu d'utiliser tf.Print , nous allons créer notre propre opération d'impression de tensorflow via tf.pyfunc . Comme pour les assertions, nous devons nous assurer que notre méthode s'exécute.

def get_log_lik_verbose(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  def _log_lik(precisions):
    # An internal method we'll make into a TensorFlow operation via tf.py_func
    def _print_precisions(precisions):
      print('precisions:\n', precisions)
      return False  # operations must return something!
    # Turn our method into a TensorFlow operation
    print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)

    # Assertions are also operations, and some care needs to be taken to ensure
    # that they're executed
    assert_op = tf.assert_equal(
        precisions, tf.linalg.matrix_transpose(precisions),
        message='not symmetrical', summarize=4, name='symmetry_check')

    # The control_dependencies statement forces its arguments to be executed
    # before subsequent operations
    with tf.control_dependencies([print_op, assert_op]):
      return (log_lik_data(precisions, replicated_data) +
              log_lik_prior(precisions))

  return _log_lik

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  init_precision = tf.eye(2)[tf.newaxis, ...]
  log_lik_fn = get_log_lik_verbose(my_data)
  # we'll just do a few steps here
  num_results = 10
  num_burnin_steps = 10
  states = tfp.mcmc.sample_chain(
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      current_state=[
          init_precision,
      ],
      kernel=tfp.mcmc.HamiltonianMonteCarlo(
          target_log_prob_fn=log_lik_fn,
          step_size=0.1,
          num_leapfrog_steps=3),
      trace_fn=None,
      seed=123)

try:
  states = sample()
except Exception as e:
  # shorten the giant stack trace
  lines = str(e).split('\n')
  print('\n'.join(lines[:5]+['...']+lines[-3:]))

precisions:
 [[[1. 0.]
  [0. 1.]]]
precisions:
 [[[1. 0.]
  [0. 1.]]]
precisions:
 [[[ 0.24315196 -0.2761638 ]
  [-0.33882257  0.8622    ]]]
 assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
     [[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]

Function call stack:
sample
...
Function call stack:
sample

Pourquoi cela échoue

La toute première nouvelle valeur de paramètre que l'échantillonneur essaie est une matrice asymétrique. Cela provoque l'échec de la décomposition de Cholesky, car elle n'est définie que pour les matrices symétriques (et définies positivement).

Le problème ici est que notre paramètre d'intérêt est une matrice de précision, et les matrices de précision doivent être réelles, symétriques et définies positives. L'échantillonneur ne connaît rien de cette contrainte (sauf éventuellement par gradients), il est donc tout à fait possible que l'échantillonneur propose une valeur invalide, conduisant à une exception, notamment si la taille du pas est importante.

Avec l'échantillonneur hamiltonien de Monte Carlo, nous pouvons peut-être contourner le problème en utilisant une très petite taille de pas, car le gradient devrait éloigner les paramètres des régions invalides, mais de petites tailles de pas signifient une convergence lente. Avec un sampler Metropolis-Hastings, qui ne connaît rien aux gradients, on est condamné.

Version 2 : reparamétrage en paramètres non contraints

Il existe une solution simple au problème ci-dessus : nous pouvons reparamétrer notre modèle de telle sorte que les nouveaux paramètres n'aient plus ces contraintes. TFP fournit un ensemble d'outils utiles - des bijecteurs - pour faire exactement cela.

Reparamétrage avec bijecteurs

Notre matrice de précision doit être réelle et symétrique ; nous voulons une paramétrisation alternative qui n'a pas ces contraintes. Un point de départ est une factorisation de Cholesky de la matrice de précision. Les facteurs de Cholesky sont toujours contraints - ils sont triangulaires inférieurs et leurs éléments diagonaux doivent être positifs. Cependant, si on prend le log des diagonales du facteur de Cholesky, les logs ne sont plus contraints d'être positifs, et puis si on aplatit la partie triangulaire inférieure en un vecteur 1-D, on n'a plus la contrainte triangulaire inférieure . Le résultat dans notre cas sera un vecteur de longueur 3 sans contraintes.

(Le manuel Stan a un grand chapitre sur l' utilisation de transformations pour éliminer les différents types de contraintes sur les paramètres.)

Ce reparamétrage a peu d'effet sur notre fonction de vraisemblance du journal de données - il suffit d'inverser notre transformation pour récupérer la matrice de précision - mais l'effet sur le prior est plus compliqué. Nous avons précisé que la probabilité d'une matrice de précision donnée est donnée par la distribution de Wishart ; quelle est la probabilité de notre matrice transformée ?

Rappelons que si l' on applique une fonction monotones \(g\) à un 1-D variable aléatoire \(X\), \(Y = g(X)\), la densité pour \(Y\) est donnée par

\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]

Le dérivé de \(g^{-1}\) comptes terme pour la façon dont \(g\) change volumes locaux. Pour les variables aléatoires dimensions plus élevées, le facteur de correction est la valeur absolue du déterminant de la jacobienne de \(g^{-1}\) (voir ici ).

Nous devrons ajouter un jacobien de la transformée inverse dans notre fonction de vraisemblance a priori log. Heureusement, de TFP Bijector classe peut prendre soin de cela pour nous.

La Bijector classe est utilisée pour la représentation de fonctions inversibles, lisses utilisés pour modifier des variables dans les fonctions de densité de probabilité. Bijectors ont tous un forward() méthode qui effectue une transformation, une inverse() méthode qui radiers, et forward_log_det_jacobian() et inverse_log_det_jacobian() méthodes qui fournissent les corrections jacobiens dont nous avons besoin lorsque nous reparaterize un pdf.

TFP fournit une collection de bijectors utiles que nous pouvons combiner à travers la composition via la Chain opérateur pour former des transformations assez compliqué. Dans notre cas, nous allons composer les 3 bijecteurs suivants (les opérations dans la chaîne s'effectuent de droite à gauche) :

1. La première étape de notre transformation consiste à effectuer une factorisation de Cholesky sur la matrice de précision. Il n'y a pas de classe Bijector pour ça ; cependant, le CholeskyOuterProduct bijector prend le produit de 2 facteurs Cholesky. Nous pouvons utiliser l'inverse de cette opération en utilisant l' Invert opérateur.
2. L'étape suivante consiste à prendre le log des éléments diagonaux du facteur de Cholesky. Nous accomplissons cela via le TransformDiagonal bijector et l'inverse de l' Exp bijector.
3. Enfin , nous aplatir la partie triangulaire inférieure de la matrice à un vecteur en utilisant l'inverse de la FillTriangular bijector.

# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
    # step 3: flatten the lower triangular portion of the matrix
    tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
    # step 2: take the log of the diagonals    
    tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
    # step 1: decompose the precision matrix into its Cholesky factors
    tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])

# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)

# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)

print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()

print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())

single input:
m:
 [[1. 2.]
 [2. 8.]]
precision_to_unconstrained(m):
 [0.6931472 2.        0.       ]
inverse(precision_to_unconstrained(m)):
 [[1. 2.]
 [2. 8.]]

tensor of inputs:
m2:
 [[[1. 2.]
  [2. 8.]]

 [[1. 0.]
  [0. 1.]]]
precision_to_unconstrained(m2):
 [[0.6931472 2.        0.       ]
 [0.        0.        0.       ]]
inverse(precision_to_unconstrained(m2)):
 [[[1. 2.]
  [2. 8.]]

 [[1. 0.]
  [0. 1.]]]

Le TransformedDistribution classe automatise le processus consistant à appliquer une bijector à une distribution et mise à la correction nécessaire pour jacobienne log_prob() . Notre nouveau prieur devient :

def log_lik_prior_transformed(transformed_precisions):
  rv_precision = tfd.TransformedDistribution(
      tfd.WishartTriL(
          df=PRIOR_DF,
          scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
          validate_args=VALIDATE_ARGS,
          allow_nan_stats=ALLOW_NAN_STATS),
      bijector=precision_to_unconstrained,
      validate_args=VALIDATE_ARGS)
  return rv_precision.log_prob(transformed_precisions)

# Check against the numpy implementation.  Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
    transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
  print('tensorflow:', lik_tf[i])

0
numpy: -0.8488930160357633
tensorflow: -0.84889317
1
numpy: -7.305657151741624
tensorflow: -7.305659

Nous avons juste besoin d'inverser la transformation pour notre probabilité de journal de données :

precision = precision_to_unconstrained.inverse(transformed_precision)

Puisque nous voulons en fait la factorisation de Cholesky de la matrice de précision, il serait plus efficace de faire ici un inverse partiel. Cependant, nous laisserons l'optimisation pour plus tard et laisserons l'inverse partiel comme exercice pour le lecteur.

def log_lik_data_transformed(transformed_precisions, replicated_data):
  # We recover the precision matrix by inverting our bijector.  This is
  # inefficient since we really want the Cholesky decomposition of the
  # precision matrix, and the bijector has that in hand during the inversion,
  # but we'll worry about efficiency later.
  n = tf.shape(transformed_precisions)[0]
  precisions = precision_to_unconstrained.inverse(transformed_precisions)
  precisions_cholesky = tf.linalg.cholesky(precisions)
  covariances = tf.linalg.cholesky_solve(
      precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
  rv_data = tfd.MultivariateNormalFullCovariance(
      loc=tf.zeros([n, 2]),
      covariance_matrix=covariances,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)

  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
    transformed_precisions, replicated_data).numpy()

for i in range(precisions.shape[0]):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.8182

Encore une fois, nous enveloppons nos nouvelles fonctions dans une fermeture.

def get_log_lik_transformed(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik_transformed(transformed_precisions):
    return (log_lik_data_transformed(transformed_precisions, replicated_data) +
            log_lik_prior_transformed(transformed_precisions))

  return _log_lik_transformed

# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)

[-431.5611]

Échantillonnage

Maintenant que nous n'avons plus à nous soucier de l'explosion de notre échantillonneur à cause de valeurs de paramètres invalides, générons de vrais échantillons.

L'échantillonneur fonctionne avec la version sans contrainte de nos paramètres, nous devons donc transformer notre valeur initiale en sa version sans contrainte. Les échantillons que nous générons seront également tous sous leur forme non contrainte, nous devons donc les retransformer. Les bijecteurs sont vectorisés, c'est donc facile à faire.

# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
    [[0.5 + np.random.uniform(), 0.0],
     [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
    dtype=np.float32)
initial_value =  initial_value_cholesky.dot(
  initial_value_cholesky.T)[np.newaxis, ...]

# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
  initial_value).numpy()

# Sample!
@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)

  num_results = 1000
  num_burnin_steps = 1000

  states, is_accepted = tfp.mcmc.sample_chain(
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      current_state=[
          initial_value_transformed,
      ],
      kernel=tfp.mcmc.HamiltonianMonteCarlo(
          target_log_prob_fn=log_lik_fn,
          step_size=0.1,
          num_leapfrog_steps=3),
      trace_fn=lambda _, pkr: pkr.is_accepted,
      seed=123)
  # transform samples back to their constrained form
  precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
  return states, precision_samples, is_accepted

states, precision_samples, is_accepted = sample()

Comparons la moyenne de la sortie de notre échantillonneur à la moyenne a posteriori analytique !

print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Sample mean:
 [[ 1.4315274  -0.25587553]
 [-0.25587553  0.5740424 ]]

Nous sommes loin ! Voyons pourquoi. Regardons d'abord nos échantillons.

np.reshape(precision_samples, [-1, 2, 2])

array([[[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       ...,

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]]], dtype=float32)

Euh oh - on dirait qu'ils ont tous la même valeur. Voyons pourquoi.

La kernel_results_ variable est un tuple nommé qui donne des informations sur l'échantillonneur à chaque état. Le is_accepted champ est la clé ici.

# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))

[False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False]
Fraction of samples accepted: 0.0

Tous nos échantillons ont été rejetés ! Vraisemblablement, notre taille de pas était trop grande. Je choisis stepsize=0.1 purement arbitraire.

Version 3 : échantillonnage avec une taille de pas adaptative

Étant donné que l'échantillonnage avec mon choix arbitraire de taille de pas a échoué, nous avons quelques points à l'ordre du jour :

1. mettre en œuvre une taille de pas adaptative, et
2. effectuer des vérifications de convergence.

Il y a un code agréable exemple dans tensorflow_probability/python/mcmc/hmc.py pour la mise en œuvre des tailles de pas d' adaptation. Je l'ai adapté ci-dessous.

Notez qu'il ya un séparé sess.run() instruction pour chaque étape. C'est vraiment utile pour le débogage, car cela nous permet d'ajouter facilement des diagnostics par étape si besoin est. Par exemple, nous pouvons afficher les progrès incrémentiels, chronométrer chaque étape, etc.

Astuce: Une façon apparemment commune à gâcher votre échantillonnage est d'avoir votre graphique dans grandir la boucle. (La raison de finaliser le graphique avant l'exécution de la session est d'éviter de tels problèmes.) Si vous n'avez pas utilisé finalize(), cependant, une vérification de débogage utile si votre code ralentit à un crawl est d'imprimer le graphique taille à chaque étape par len(mygraph.get_operations()) - si la longueur augmente, que vous faites probablement mal quelque chose.

Nous allons gérer ici 3 chaînes indépendantes. Faire des comparaisons entre les chaînes nous aidera à vérifier la convergence.

# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3

np.random.seed(123)

initial_values = []
for i in range(N_CHAINS):
  initial_value_cholesky = np.array(
      [[0.5 + np.random.uniform(), 0.0],
       [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
      dtype=np.float32)
  initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)

initial_values_transformed = precision_to_unconstrained.forward(
  initial_values).numpy()

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_transformed(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=hmc,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states, is_accepted = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values_transformed,
      kernel=adapted_kernel,
      trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
      parallel_iterations=1)
  # transform samples back to their constrained form
  precision_samples = precision_to_unconstrained.inverse(states)
  return states, precision_samples, is_accepted

states, precision_samples, is_accepted = sample()

Une vérification rapide : notre taux d'acceptation lors de notre échantillonnage est proche de notre objectif de 0,651.

print(np.mean(is_accepted))

0.6190666666666667

Mieux encore, la moyenne et l'écart type de notre échantillon sont proches de ce que nous attendons de la solution analytique.

precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.96426415 -1.6519215 ]
 [-1.6519215   3.8614824 ]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13622096 0.25235635]
 [0.25235635 0.5394968 ]]

Vérification de la convergence

En général, nous n'aurons pas de solution analytique à comparer, nous devrons donc nous assurer que l'échantillonneur a convergé. Une vérification standard est le Gelman-Rubin \(\hat{R}\) statistique, ce qui nécessite de multiples chaînes d'échantillonnage. \(\hat{R}\) mesure le degré de variance (des moyens) entre les chaînes dépasse ce que l' on pouvait s'y attendre si les chaînes ont été distribuées de façon identique. Les valeurs de \(\hat{R}\) près de 1 sont utilisés pour indiquer la convergence approximative. Voir la source pour plus de détails.

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0038308 1.0005717]
 [1.0005717 1.0006068]]

Critique du modèle

Si nous n'avions pas de solution analytique, ce serait le moment de faire une vraie critique de modèle.

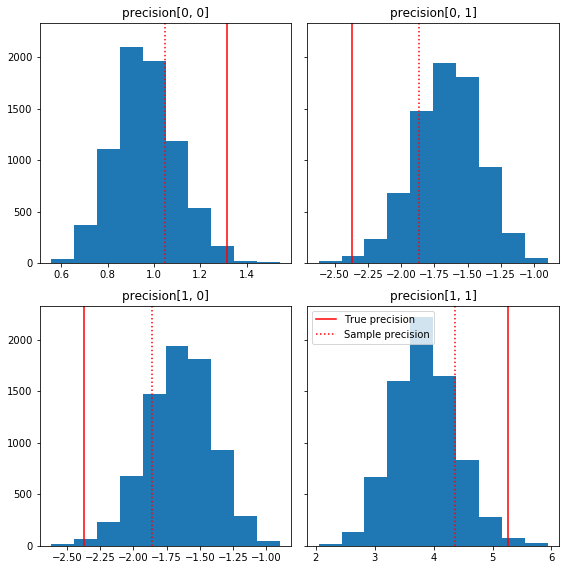
Voici quelques histogrammes rapides des composants de l'échantillon par rapport à notre vérité terrain (en rouge). Notez que les échantillons ont été réduits des valeurs de la matrice de précision de l'échantillon vers la matrice d'identité avant.

fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
  for j in range(2):
    ax = axes[i, j]
    ax.hist(precision_samples_reshaped[:, i, j])
    ax.axvline(true_precision[i, j], color='red',
               label='True precision')
    ax.axvline(sample_precision[i, j], color='red', linestyle=':',
               label='Sample precision')
    ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()

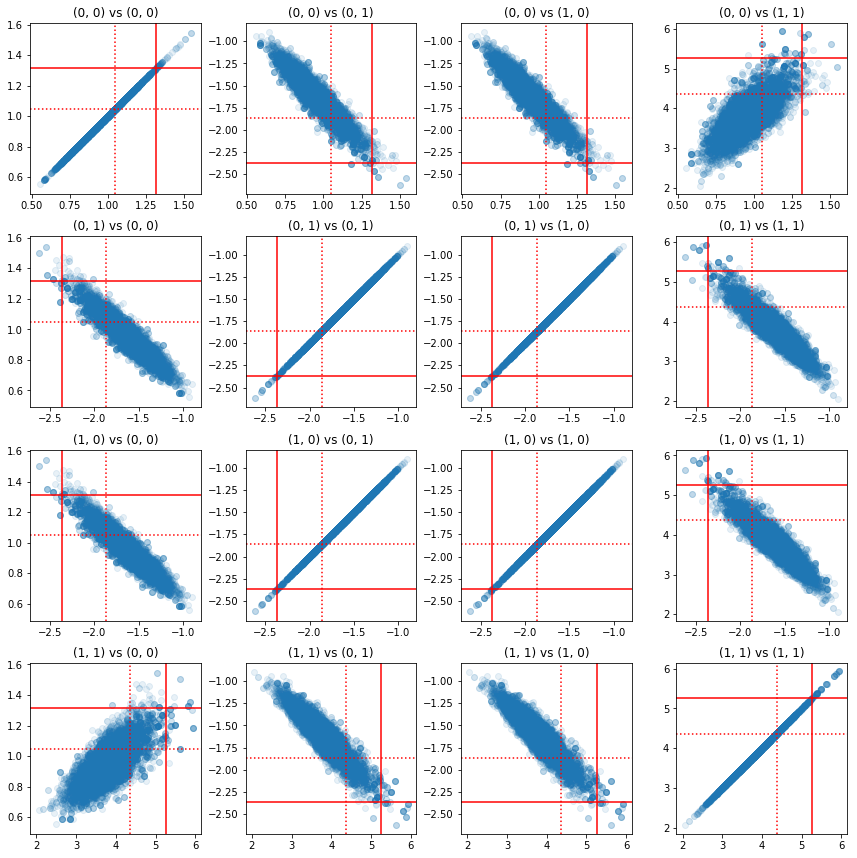
Certains nuages ​​de points de paires de composants de précision montrent qu'en raison de la structure de corrélation du postérieur, les vraies valeurs postérieures ne sont pas aussi improbables qu'elles le paraissent des marginaux ci-dessus.

fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
  for j1 in range(2):
    index1 = 2 * i1 + j1
    for i2 in range(2):
      for j2 in range(2):
        index2 = 2 * i2 + j2
        ax = axes[index1, index2]
        ax.scatter(precision_samples_reshaped[:, i1, j1],
                   precision_samples_reshaped[:, i2, j2], alpha=0.1)
        ax.axvline(true_precision[i1, j1], color='red')
        ax.axhline(true_precision[i2, j2], color='red')
        ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
        ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
        ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()

Version 4 : échantillonnage plus simple des paramètres contraints

Les bijecteurs ont simplifié l'échantillonnage de la matrice de précision, mais il y avait une bonne quantité de conversion manuelle vers et à partir de la représentation sans contrainte. Il existe un moyen plus simple !

Le noyau de transition transformé

Le TransformedTransitionKernel simplifie ce processus. Il enveloppe votre échantillonneur et gère toutes les conversions. Il prend comme argument une liste de bijecteurs qui mappent des valeurs de paramètres non contraintes à des valeurs contraintes. Donc , ici nous avons besoin de l'inverse de la precision_to_unconstrained bijector nous avons utilisé ci - dessus. Nous pourrions utiliser tfb.Invert(precision_to_unconstrained) , mais cela impliquerait de prendre des inverses des inverses (tensorflow est pas assez intelligent pour simplifier tf.Invert(tf.Invert()) à tf.Identity()) , donc au lieu que nous Je vais juste écrire un nouveau bijecteur.

Bijecteur contraignant

# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
    # step 3: take the product of Cholesky factors
    tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
    # step 2: exponentiate the diagonals    
    tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
    # step 1: map a vector to a lower triangular matrix
    tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])

# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()

print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)

m:
 [[1.0, 2.0], [2.0, 8.0]]
unconstrained_to_precision.inverse(m):
 [0.6931472 2.        0.       ]
forward(unconstrained_to_precision.inverse(m)):
 [[1. 2.]
 [2. 8.]]

Échantillonnage avec TransformedTransitionKernel

Avec le TransformedTransitionKernel , nous n'avons plus à faire des transformations manuelles de nos paramètres. Nos valeurs initiales et nos échantillons sont tous des matrices de précision ; il suffit de passer notre ou nos bijecteur(s) sans contrainte au noyau et il s'occupe de toutes les transformations.

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  ttk = tfp.mcmc.TransformedTransitionKernel(
      inner_kernel=hmc, bijector=unconstrained_to_precision)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=ttk,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values,
      kernel=adapted_kernel,
      trace_fn=None,
      parallel_iterations=1)
  # transform samples back to their constrained form
  return states

precision_samples  = sample()

Vérification de la convergence

Le \(\hat{R}\) contrôle de convergence semble bon!

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0013582 1.0019467]
 [1.0019467 1.0011805]]

Comparaison avec le postérieur analytique

Encore une fois, vérifions par rapport au postérieur analytique.

# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])

print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.96687526 -1.6552585 ]
 [-1.6552585   3.867676  ]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13329624 0.24913791]
 [0.24913791 0.53983927]]

Optimisations

Maintenant que les choses fonctionnent de bout en bout, faisons une version plus optimisée. La vitesse n'a pas trop d'importance pour cet exemple, mais une fois que les matrices deviennent plus grandes, quelques optimisations feront une grande différence.

Une grande amélioration de vitesse que nous pouvons faire est de reparamétrer en termes de décomposition de Cholesky. La raison en est que notre fonction de vraisemblance des données nécessite à la fois les matrices de covariance et de précision. Inversion de matrice est cher (\(O(n^3)\) pour un \(n \times n\) matrice), et si nous paramétrons soit en termes de la covariance ou la matrice de précision, nous avons besoin de faire une inversion pour obtenir l'autre.

Pour rappel, un vrai, définie positive, symétrique matrice \(M\) peut être décomposé en un produit de la forme \(M = L L^T\) où la matrice \(L\) est triangulaire inférieure et possède des diagonales positifs. Compte tenu de la décomposition de Cholesky de \(M\), nous pouvons obtenir plus efficacement à la fois \(M\) (le produit d'une plus faible et une matrice triangulaire supérieure) et \(M^{-1}\) (via back-substitution). La factorisation de Cholesky elle-même n'est pas bon marché à calculer, mais si nous paramétrons en termes de facteurs de Cholesky, nous n'avons besoin de calculer que la factorisation de Choleksy des valeurs initiales des paramètres.

Utilisation de la décomposition de Cholesky de la matrice de covariance

TFP dispose d' une version de la distribution normale à plusieurs variables, MultivariateNormalTriL , qui est paramétrés en fonction du facteur de Cholesky de la matrice de covariance. Donc, si nous devions paramétrer en termes de facteur de Cholesky de la matrice de covariance, nous pourrions calculer efficacement la vraisemblance du journal des données. Le défi consiste à calculer la probabilité de log a priori avec une efficacité similaire.

Si nous avions une version de la distribution de Wishart inverse qui fonctionnait avec les facteurs d'échantillons de Cholesky, nous serions prêts. Hélas, nous ne le faisons pas. (Cependant, l'équipe apprécierait les soumissions de code !) Comme alternative, nous pouvons utiliser une version de la distribution Wishart qui fonctionne avec des facteurs de Cholesky d'échantillons avec une chaîne de bijecteurs.

Pour le moment, il nous manque quelques bijecteurs de stock pour rendre les choses vraiment efficaces, mais je veux montrer le processus comme un exercice et une illustration utile de la puissance des bijecteurs de TFP.

Une distribution de Wishart qui fonctionne sur les facteurs de Cholesky

La Wishart distribution a un drapeau utile, input_output_cholesky , qui précise que les entrées et les matrices de sortie doivent être des facteurs Cholesky. Il est plus efficace et numériquement plus avantageux de travailler avec les facteurs de Cholesky qu'avec des matrices complètes, c'est pourquoi cela est souhaitable. Un point important sur la sémantique du drapeau: il est seulement une indication que la représentation de l'entrée et de sortie à la distribution doit changer - il n'indique une reparamétrage complète de la distribution, ce qui impliquerait une correction jacobienne à la log_prob() une fonction. Nous voulons en fait faire ce reparamétrage complet, nous allons donc construire notre propre distribution.

# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices.  Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).

class CholeskyWishart(tfd.TransformedDistribution):
  """Wishart distribution reparameterized to use Cholesky factors."""
  def __init__(self,
      df,
      scale_tril,
      validate_args=False,
      allow_nan_stats=True,
      name='CholeskyWishart'):
    # Wishart has a bunch of methods that we want to support but not
    # implement.  We'll subclass TransformedDistribution here to take care of
    # those.  We'll override the few for which speed is critical and implement
    # them with a separate Wishart for which input_output_cholesky=True
    super(CholeskyWishart, self).__init__(
        distribution=tfd.WishartTriL(
            df=df,
            scale_tril=scale_tril,
            input_output_cholesky=False,
            validate_args=validate_args,
            allow_nan_stats=allow_nan_stats),
        bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
        validate_args=validate_args,
        name=name
    )
    # Here's the Cholesky distribution we'll use for log_prob() and sample()
    self.cholesky = tfd.WishartTriL(
        df=df,
        scale_tril=scale_tril,
        input_output_cholesky=True,
        validate_args=validate_args,
        allow_nan_stats=allow_nan_stats)

  def _log_prob(self, x):
    return (self.cholesky.log_prob(x) +
            self.bijector.inverse_log_det_jacobian(x, event_ndims=2))

  def _sample_n(self, n, seed=None):
    return self.cholesky._sample_n(n, seed)

# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)

@tf.function(autograph=False)
def compute_log_prob(m):
  w_transformed = tfd.TransformedDistribution(
      tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
      bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
  w_optimized = CholeskyWishart(
      df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
  log_prob_transformed = w_transformed.log_prob(m)
  log_prob_optimized = w_optimized.log_prob(m)
  return log_prob_transformed, log_prob_optimized

for matrix in [np.eye(2, dtype=np.float32),
               np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
  log_prob_transformed, log_prob_optimized = [
      t.numpy() for t in compute_log_prob(matrix)]
  print('Transformed Wishart:', log_prob_transformed)
  print('Optimized Wishart', log_prob_optimized)

Transformed Wishart: -0.84889317
Optimized Wishart -0.84889317
Transformed Wishart: -99.269455
Optimized Wishart -99.269455

Construire une distribution de Wishart inverse

Nous avons notre matrice de covariance \(C\) décomposé en \(C = L L^T\) où \(L\) est triangulaire inférieure et a une diagonale positive. Nous voulons connaître la probabilité de \(L\) étant donné que \(C \sim W^{-1}(\nu, V)\) où \(W^{-1}\) est l'inverse Wishart.

L'inverse Wishart a la propriété que si \(C \sim W^{-1}(\nu, V)\), la matrice de précision \(C^{-1} \sim W(\nu, V^{-1})\). Ainsi , nous pouvons obtenir la probabilité de \(L\) via un TransformedDistribution qui prend comme paramètres de la distribution Wishart et un bijector qui mappe le facteur Cholesky de la matrice de précision à un facteur de Cholesky de son inverse.

Un simple (mais pas super efficace) façon d'obtenir du facteur Cholesky de \(C^{-1}\) à \(L\) est d'inverser le facteur de Cholesky par retour de résolution, formant alors la matrice de covariance de ces facteurs inversés, et puis en faisant une factorisation de Cholesky .

Que la décomposition de Cholesky de \(C^{-1} = M M^T\). \(M\) est triangulaire inférieure, de sorte que nous pouvons inverser à l'aide du MatrixInverseTriL bijector.

La formation \(C\) de \(M^{-1}\) est un peu délicat: \(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\). \(M\) est triangulaire inférieure, de sorte que \(M^{-1}\) sera également triangulaire inférieure, et \(M^{-T}\) sera triangulaire supérieure. Le CholeskyOuterProduct() bijector fonctionne uniquement avec des matrices triangulaires inférieures, donc nous ne pouvons pas l' utiliser pour former \(C\) de \(M^{-T}\). Notre solution de contournement est une chaîne de bijecteurs qui permutent les lignes et les colonnes d'une matrice.

Heureusement , cette logique est encapsulé dans le CholeskyToInvCholesky bijector!

Combiner toutes les pièces

# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()

print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)

numpy =
 [[ 1.0307764   0.        ]
 [-0.03031695  0.12126781]]
bijector =
 [[ 1.0307764   0.        ]
 [-0.03031695  0.12126781]]

Notre distribution finale

Notre Wishart inverse fonctionnant sur les facteurs de Cholesky est le suivant :

inverse_wishart_cholesky = tfd.TransformedDistribution(
    distribution=CholeskyWishart(
        df=PRIOR_DF,
        scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
    bijector=tfb.CholeskyToInvCholesky())

Nous avons notre Wishart inverse, mais c'est un peu lent car nous devons faire une décomposition de Cholesky dans le bijecteur. Revenons au paramétrage de la matrice de précision et voyons ce que nous pouvons y faire pour l'optimisation.

Version finale (!) : utilisant la décomposition de Cholesky de la matrice de précision

Une approche alternative consiste à travailler avec les facteurs de Cholesky de la matrice de précision. Ici, la fonction de vraisemblance a priori est facile à calculer, mais la fonction de vraisemblance du journal des données demande plus de travail car TFP n'a pas de version de la normale multivariée paramétrée par la précision.

Probabilité de log préalable optimisée

Nous utilisons la CholeskyWishart la distribution , nous avons construit ci - dessus pour construire l'avant.

# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)

def log_lik_prior_cholesky(precisions_cholesky):
  rv_precision = CholeskyWishart(
      df=PRIOR_DF,
      scale_tril=PRIOR_SCALE_CHOLESKY,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)
  return rv_precision.log_prob(precisions_cholesky)

# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
              true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
    distribution=tfd.WishartTriL(
        df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
    bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
    precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
    precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
  print('tensorflow slow:', lik_tf_slow[i])
  print('tensorflow fast:', lik_tf[i])

0
numpy: -0.8488930160357633
tensorflow slow: -0.84889317
tensorflow fast: -0.84889317
1
numpy: -7.442875031036973
tensorflow slow: -7.442877
tensorflow fast: -7.442876

Probabilité optimisée du journal de données

We can use TFP's bijectors to build our own version of the multivariate normal. Here is the key idea:

Suppose I have a column vector \(X\) whose elements are iid samples of \(N(0, 1)\). We have \(\text{mean}(X) = 0\) and \(\text{cov}(X) = I\)

Now let \(Y = A X + b\). We have \(\text{mean}(Y) = b\) and \(\text{cov}(Y) = A A^T\)

Hence we can make vectors with mean \(b\) and covariance \(C\) using the affine transform \(Ax+b\) to vectors of iid standard Normal samples provided \(A A^T = C\). The Cholesky decomposition of \(C\) has the desired property. However, there are other solutions.

Let \(P = C^{-1}\) and let the Cholesky decomposition of \(P\) be \(B\), ie \(B B^T = P\). Now

\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)

So another way to get our desired mean and covariance is to use the affine transform \(Y=B^{-T}X + b\).

Our approach (courtesy of this notebook ):

1. Use tfd.Independent() to combine a batch of 1-D Normal random variables into a single multi-dimensional random variable. The reinterpreted_batch_ndims parameter for Independent() specifies the number of batch dimensions that should be reinterpreted as event dimensions. In our case we create a 1-D batch of length 2 that we transform into a 1-D event of length 2, so reinterpreted_batch_ndims=1 .
2. Apply a bijector to add the desired covariance: tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True)) . Note that above we're multiplying our iid normal random variables by the transpose of the inverse of the Cholesky factor of the precision matrix \((B^{-T}X)\). The tfb.Invert takes care of inverting \(B\), and the adjoint=True flag performs the transpose.
3. Apply a bijector to add the desired offset: tfb.Shift(shift=shift) Note that we have to do the shift as a separate step from the initial inverted affine transform because otherwise the inverted scale is applied to the shift (since the inverse of \(y=Ax+b\) is \(x=A^{-1}y - A^{-1}b\)).

class MVNPrecisionCholesky(tfd.TransformedDistribution):
  """Multivariate normal parameterized by loc and Cholesky precision matrix."""

  def __init__(self, loc, precision_cholesky, name=None):
    super(MVNPrecisionCholesky, self).__init__(
        distribution=tfd.Independent(
            tfd.Normal(loc=tf.zeros_like(loc),
                       scale=tf.ones_like(loc)),
            reinterpreted_batch_ndims=1),
        bijector=tfb.Chain([
            tfb.Shift(shift=loc),
            tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
                                  adjoint=True)),
        ]),
        name=name)

@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
  n = tf.shape(precisions_cholesky)[0]  # number of precision matrices
  rv_data = MVNPrecisionCholesky(
      loc=tf.zeros([n, 2]),
      precision_cholesky=precisions_cholesky)
  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.81824

Combined log likelihood function

Now we combine our prior and data log likelihood functions in a closure.

def get_log_lik_cholesky(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik_cholesky(precisions_cholesky):
    return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
            log_lik_prior_cholesky(precisions_cholesky))

  return _log_lik_cholesky

Constraining bijector

Our samples are constrained to be valid Cholesky factors, which means they must be lower triangular matrices with positive diagonals. The TransformedTransitionKernel needs a bijector that maps unconstrained tensors to/from tensors with our desired constraints. We've removed the Cholesky decomposition from the bijector's inverse, which speeds things up.

unconstrained_to_precision_cholesky = tfb.Chain([
    # step 2: exponentiate the diagonals    
    tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
    # step 1: expand the vector to a lower triangular matrix
    tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])

# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)

precisions_cholesky:
 [[[ 1.         0.       ]
  [ 0.         1.       ]]

 [[ 1.1470785  0.       ]
  [-2.0647411  1.0000004]]]

inv:
 [[ 0.0000000e+00  0.0000000e+00  0.0000000e+00]
 [ 3.5762781e-07 -2.0647411e+00  1.3721828e-01]]

fwd(inv):
 [[[ 1.         0.       ]
  [ 0.         1.       ]]

 [[ 1.1470785  0.       ]
  [-2.0647411  1.0000004]]]

Initial values

We generate a tensor of initial values. We're working with Cholesky factors, so we generate some Cholesky factor initial values.

# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3

np.random.seed(123)

initial_values_cholesky = []
for i in range(N_CHAINS):
  initial_values_cholesky.append(np.array(
      [[0.5 + np.random.uniform(), 0.0],
       [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
      dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)

Sampling

We sample N_CHAINS chains using the TransformedTransitionKernel .

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_cholesky(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  ttk = tfp.mcmc.TransformedTransitionKernel(
      inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=ttk,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values,
      kernel=adapted_kernel,
      trace_fn=None,
      parallel_iterations=1)
  # transform samples back to their constrained form
  samples = tf.linalg.matmul(states, states, transpose_b=True)
  return samples

precision_samples = sample()

Convergence check

A quick convergence check looks good:

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0013583 1.0019467]
 [1.0019467 1.0011804]]

Comparing results to the analytic posterior

# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])

And again, the sample means and standard deviations match those of the analytic posterior.

print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.9668749 -1.6552604]
 [-1.6552604  3.8676758]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13329637 0.24913797]
 [0.24913797 0.53983945]]

Ok, all done! We've got our optimized sampler working.