 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Escrevi este caderno como um estudo de caso para aprender a Probabilidade do TensorFlow. O problema que escolhi resolver é estimar uma matriz de covariância para amostras de uma variável aleatória gaussiana de média 0 2-D. O problema tem alguns recursos interessantes:
- Se usarmos um Wishart inverso anterior para a covariância (uma abordagem comum), o problema tem uma solução analítica, então podemos verificar nossos resultados.
- O problema envolve a amostragem de um parâmetro restrito, o que adiciona alguma complexidade interessante.
- A solução mais direta não é a mais rápida, portanto, há algum trabalho de otimização a ser feito.
Decidi escrever minhas experiências à medida que avançava. Levei um tempo para entender os pontos mais delicados do TFP, então este notebook começa de forma bastante simples e então gradualmente passa para recursos mais complicados do TFP. Encontrei muitos problemas ao longo do caminho e tentei capturar os processos que me ajudaram a identificá-los e as soluções alternativas que acabei encontrando. Tentei incluir muitos detalhes (incluindo lotes de testes para certificar-se de etapas individuais estão corretas).
Por que aprender a Probabilidade do TensorFlow?
Achei a Probabilidade do TensorFlow atraente para meu projeto por alguns motivos:
- A probabilidade do TensorFlow permite que você desenvolva protótipos de modelos complexos interativamente em um notebook. Você pode quebrar seu código em pequenos pedaços que você pode testar interativamente e com testes de unidade.
- Quando estiver pronto para escalar, você pode aproveitar toda a infraestrutura que temos para fazer o TensorFlow rodar em vários processadores otimizados em várias máquinas.
- Finalmente, embora eu realmente goste de Stan, acho bastante difícil depurar. Você deve escrever todo o seu código de modelagem em uma linguagem autônoma que tenha muito poucas ferramentas para permitir que você cutuque seu código, inspecione estados intermediários e assim por diante.
A desvantagem é que o TensorFlow Probability é muito mais recente do que Stan e PyMC3, então a documentação é um trabalho em andamento e há muitas funcionalidades que ainda precisam ser desenvolvidas. Felizmente, descobri que a base do TFP é sólida e foi projetada de forma modular que permite estender sua funcionalidade de forma bastante direta. Neste bloco de notas, além de solucionar o estudo de caso, mostrarei algumas maneiras de estender a TFP.
Para quem é isso
Estou assumindo que os leitores estão chegando a este notebook com alguns pré-requisitos importantes. Você deve:
- Conhecer os fundamentos da inferência bayesiana. (Se você não fizer isso, um muito bom primeiro livro é de Estatística Rethinking )
- Ter alguma familiaridade com uma biblioteca de amostragem MCMC, por exemplo, Stan / PyMC3 / BUGS
- Tem uma sólida compreensão NumPy (Uma boa introdução é Python para Análise de Dados )
- Ter pelo menos familiaridade com TensorFlow , mas não necessariamente perícia. ( Aprendizagem TensorFlow é bom, mas meio evolução rápida do TensorFlow que a maioria dos livros será um pouco datados. De Stanford CS20 curso também é bom.)
Primeira tentativa
Aqui está minha primeira tentativa de resolver o problema. Spoiler: minha solução não funciona e serão necessárias várias tentativas para acertar as coisas! Embora o processo demore um pouco, cada tentativa abaixo foi útil para aprender uma nova parte da TFP.
Uma nota: o TFP não implementa atualmente a distribuição inversa de Wishart (veremos no final como rolar nosso próprio Wishart inverso), então, em vez disso, mudarei o problema para estimar uma matriz de precisão usando um Wishart anterior.
import collections
import math
import os
import time
import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
Etapa 1: reúna as observações
Meus dados aqui são todos sintéticos, então isso vai parecer um pouco mais organizado do que um exemplo do mundo real. No entanto, não há razão para que você não possa gerar alguns dados sintéticos por conta própria.
Dica: Uma vez que você tenha decidido sobre a forma de seu modelo, você pode escolher alguns valores de parâmetro e usar o seu modelo escolhido para gerar alguns dados sintéticos. Como uma verificação de sanidade de sua implementação, você pode verificar se suas estimativas incluem os valores reais dos parâmetros escolhidos. Para tornar seu ciclo de depuração / teste mais rápido, você pode considerar uma versão simplificada de seu modelo (por exemplo, usar menos dimensões ou menos amostras).
Dica: É mais fácil trabalhar com o seu observações como matrizes Numpy. Uma coisa importante a notar é que o NumPy, por padrão, usa float64, enquanto o TensorFlow, por padrão, usa float32.
Em geral, as operações do TensorFlow querem que todos os argumentos tenham o mesmo tipo, e você precisa fazer um cast de dados explícito para alterar os tipos. Se você usar observações float64, precisará adicionar várias operações de elenco. NumPy, em contraste, cuidará da projeção automaticamente. Por isso, é muito mais fácil de converter seus dados Numpy em float32 que é para forçar TensorFlow ao uso float64.
Escolha alguns valores de parâmetro
# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)
# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))
[[4. 1.8] [1.8 1. ]] eigenvalues: [4.843075 0.15692513]
Gere algumas observações sintéticas
Note-se que TensorFlow Probabilidade usa a convenção de que a dimensão inicial (s) dos seus dados representam os índices de amostra, e a dimensão final (s) dos seus dados representam a dimensionalidade das suas amostras.
Aqui queremos 100 amostras, cada um dos quais é um vetor de comprimento 2. Vamos gerar uma série my_data com forma (100, 2). my_data[i, :] representa a \(i\)th amostra, e é um vector de comprimento 2.
(Lembre-se de fazer my_data têm o tipo float32!)
# Set the seed so the results are reproducible.
np.random.seed(123)
# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
mean=true_mean, cov=true_cov, size=100,
check_valid='ignore').astype(np.float32)
my_data.shape
(100, 2)
Verifique a sanidade das observações
Uma fonte potencial de bugs é bagunçar seus dados sintéticos! Vamos fazer algumas verificações simples.
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()
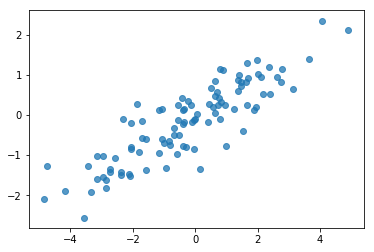
print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)
mean of observations: [-0.24009615 -0.16638893] true mean: [0. 0.]
print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)
covariance of observations: [[3.95307734 1.68718486] [1.68718486 0.94910269]] true covariance: [[4. 1.8] [1.8 1. ]]
Ok, nossas amostras parecem razoáveis. Próxima Etapa.
Etapa 2: Implementar a função de verossimilhança no NumPy
A principal coisa que precisaremos escrever para realizar nossa amostragem MCMC em TF Probability é uma função de log de verossimilhança. Em geral, é um pouco mais complicado escrever TF do que NumPy, então acho útil fazer uma implementação inicial em NumPy. Eu vou dividir a função de verossimilhança em 2 peças, uma função de probabilidade de dados que corresponde a \(P(data | parameters)\) e uma função de probabilidade antes que corresponde a \(P(parameters)\).
Observe que essas funções NumPy não precisam ser superotimizadas / vetorizadas, pois o objetivo é apenas gerar alguns valores para teste. A correção é a consideração chave!
Primeiro, implementaremos a peça de probabilidade do registro de dados. Isso é muito simples. A única coisa a lembrar é que trabalharemos com matrizes de precisão, portanto, parametrizaremos de acordo.
def log_lik_data_numpy(precision, data):
# np.linalg.inv is a really inefficient way to get the covariance matrix, but
# remember we don't care about speed here
cov = np.linalg.inv(precision)
rv = scipy.stats.multivariate_normal(true_mean, cov)
return np.sum(rv.logpdf(data))
# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)
-280.81822950593767
Nós vamos usar um Wishart prévia para a matriz de precisão uma vez que há uma solução analítica para a posterior (ver tabela prática do Wikipedia de priores conjugadas ).
A distribuição de Wishart tem 2 parâmetros:
- o número de graus de liberdade (rotulado \(\nu\) na Wikipedia)
- uma matriz de escala (marcado \(V\) em Wikipedia)
A média de uma distribuição de Wishart com parâmetros \(\nu, V\) é \(E[W] = \nu V\), e a variância é \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)
Alguns intuição útil: É possível gerar uma amostra de Wishart, gerando \(\nu\) independente chama \(x_1 \ldots x_{\nu}\) de uma variável aleatória normal multivariada com média 0 e covariância \(V\) e, em seguida, formando a soma \(W = \sum_{i=1}^{\nu} x_i x_i^T\).
Se você redimensionar amostras Wishart, dividindo-as por \(\nu\), você começa a matriz de covariância amostra da \(x_i\). Esta matriz covariância amostra deve tender para \(V\) como \(\nu\) aumenta. Quando \(\nu\) é pequeno, há muita variação na matriz covariância amostra, de modo pequenos valores de \(\nu\) correspondem aos antecedentes mais fracas e grandes valores de \(\nu\) correspondem aos antecedentes mais fortes. Note-se que \(\nu\) deve ser pelo menos tão grande como a dimensão do espaço que você está de amostragem ou você vai gerar matrizes singulares.
Usaremos \(\nu = 3\) por isso temos um fraco antes, e vamos dar \(V = \frac{1}{\nu} I\) que vai puxar a nossa estimativa de covariância em direção à identidade (lembre-se que a média é \(\nu V\)).
PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF
def log_lik_prior_numpy(precision):
rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
return rv.logpdf(precision)
# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)
-9.103606346649766
A distribuição de Wishart é o conjugado antes para a estimativa da matriz de precisão de um multivariada normal com média conhecida \(\mu\).
Suponha que os parâmetros Wishart anteriores são \(\nu, V\) e que temos \(n\) observações do nosso e normal multivariada \(x_1, \ldots, x_n\). Os parâmetros posteriores são \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\).
n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
(v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))
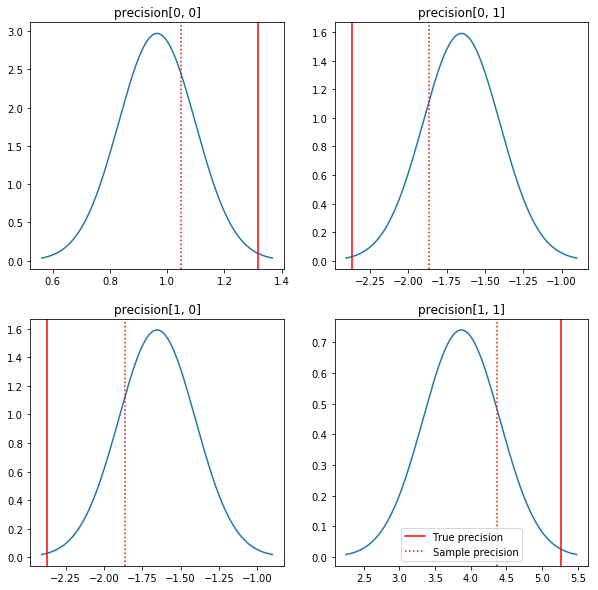
Um gráfico rápido dos posteriores e dos valores verdadeiros. Observe que os posteriores estão próximos aos posteriores da amostra, mas estão um pouco encolhidos em direção à identidade. Observe também que os valores verdadeiros estão muito longe do modo do posterior - presumivelmente porque anterior não é uma correspondência muito boa para nossos dados. Em um problema real que provavelmente faria melhor com algo parecido com um escalado inversa Wishart prévia para a covariância (ver, por exemplo, de Andrew Gelman comentário sobre o assunto), mas, em seguida, não teríamos uma boa posterior análise.
sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
for j in range(2):
ax = axes[i, j]
loc = posterior_mean[i, j]
scale = posterior_sd[i, j]
xmin = loc - 3.0 * scale
xmax = loc + 3.0 * scale
x = np.linspace(xmin, xmax, 1000)
y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
ax.plot(x, y)
ax.axvline(true_precision[i, j], color='red', label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()
Etapa 3: implementar a função de verossimilhança no TensorFlow
Spoiler: Nossa primeira tentativa não vai funcionar; vamos falar sobre o porquê abaixo.
Dica: use TensorFlow modo ansioso ao desenvolver suas funções de verossimilhança. Modo ansioso faz TF se comportam mais como NumPy - tudo executado imediatamente, para que possa depurar interativamente em vez de ter que usar Session.run() . Veja as notas aqui .
Preliminar: Classes de distribuição
TFP tem uma coleção de classes de distribuição que usaremos para gerar nossas probabilidades de log. Uma coisa a se notar é que essas classes funcionam com tensores de amostras em vez de apenas amostras únicas - isso permite a vetorização e acelerações relacionadas.
Uma distribuição pode funcionar com um tensor de amostras de 2 maneiras diferentes. É mais simples ilustrar essas 2 maneiras com um exemplo concreto envolvendo uma distribuição com um único parâmetro escalar. Vou usar o Poisson distribuição, que tem uma rate parâmetro.
- Se criarmos um Poisson com um único valor para a
rateparâmetro, uma chamada para a suasample()método retorna um único valor. Este valor é chamado de umevent, e neste caso os eventos são todos escalares. - Se criarmos um Poisson com um tensor de valores para a
rateparâmetro, uma chamada para a suasample()método agora retorna vários valores, um para cada valor no tensor taxa. O objecto actua como uma colecção de Poisson independentes, cada um com a sua própria taxa, e cada um dos valores devolvidos por uma chamada parasample()corresponde a um destes Poisson. Esta coleção de eventos identicamente distribuídos independentes, mas não é chamado umbatch. - A
sample()método leva umsample_shapeparâmetro o qual o padrão de um tuplo vazio. Passando um valor não-vazia parasample_shaperesulta na amostra retorno de vários lotes. Esta coleção de lotes é chamado desample.
Uma distribuição de log_prob() método consome dados de uma forma que paralelos como sample() gera. log_prob() retorna probabilidades para amostras, ou seja, para múltiplos, lotes independentes de eventos.
- Se temos o nosso objeto Poisson que foi criada com um escalar
rate, cada lote é um escalar, e se passar em um tensor de amostras, vamos sair um tensor do mesmo tamanho de probabilidades de log. - Se temos o nosso objeto Poisson que foi criada com um tensor da forma
Tdaratevalores, cada lote é um tensor de formaT. Se passarmos em um tensor de amostras de forma D, T, obteremos um tensor de probabilidades logarítmicas de forma D, T.
Abaixo estão alguns exemplos que ilustram esses casos. Veja este notebook para um tutorial mais detalhado sobre eventos, lotes, e formas.
# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))
# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters. Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))
print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())
iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385] draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]
Probabilidade de registro de dados
Primeiro, implementaremos a função de verossimilhança do registro de dados.
VALIDATE_ARGS = True
ALLOW_NAN_STATS = False
Uma diferença importante do caso NumPy é que nossa função de verossimilhança do TensorFlow precisará lidar com vetores de matrizes de precisão, em vez de apenas matrizes únicas. Vetores de parâmetros serão usados quando amostrarmos de várias cadeias.
Criaremos um objeto de distribuição que funciona com um lote de matrizes de precisão (ou seja, uma matriz por cadeia).
Ao calcular as probabilidades de log de nossos dados, precisaremos que nossos dados sejam replicados da mesma maneira que nossos parâmetros para que haja uma cópia por variável de lote. A forma de nossos dados replicados deve ser a seguinte:
[sample shape, batch shape, event shape]
Em nosso caso, a forma do evento é 2 (já que estamos trabalhando com gaussianas 2-D). A forma da amostra é 100, uma vez que temos 100 amostras. A forma do lote será apenas o número de matrizes de precisão com as quais estamos trabalhando. É um desperdício replicar os dados cada vez que chamamos a função de verossimilhança, portanto, replicaremos os dados antecipadamente e passaremos a versão replicada.
Note-se que esta é uma implementação ineficiente: MultivariateNormalFullCovariance é caro em relação a algumas alternativas que falaremos na seção de otimização no final.
def log_lik_data(precisions, replicated_data):
n = tf.shape(precisions)[0] # number of precision matrices
# We're estimating a precision matrix; we have to invert to get log
# probabilities. Cholesky inversion should be relatively efficient,
# but as we'll see later, it's even better if we can avoid doing the Cholesky
# decomposition altogether.
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data). We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)
(100, 2, 2)
Dica: Uma coisa que eu encontrei para ser extremamente útil está escrevendo pequenas checagens de minhas funções TensorFlow. É realmente fácil bagunçar a vetorização no TF, então ter as funções NumPy mais simples é uma ótima maneira de verificar a saída do TF. Pense nisso como pequenos testes de unidade.
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
Probabilidade de registro anterior
O anterior é mais fácil, pois não precisamos nos preocupar com a replicação de dados.
@tf.function(autograph=False)
def log_lik_prior(precisions):
rv_precision = tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions)
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]))
print('tensorflow:', lik_tf[i])
0 numpy: -2.2351873809649625 tensorflow: -2.2351875 1 numpy: -9.103606346649766 tensorflow: -9.103608
Construir a função de verossimilhança conjunta
A função de verossimilhança do registro de dados acima depende de nossas observações, mas o amostrador não as terá. Podemos nos livrar da dependência sem usar uma variável global usando um [closure] (https://en.wikipedia.org/wiki/Closure_ (computer_programming). Closures envolvem uma função externa que constrói um ambiente contendo variáveis necessárias por um função interna.
def get_log_lik(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik(precision):
return log_lik_data(precision, replicated_data) + log_lik_prior(precision)
return _log_lik
Etapa 4: Amostra
Ok, hora de provar! Para manter as coisas simples, usaremos apenas 1 cadeia e usaremos a matriz de identidade como ponto de partida. Faremos as coisas com mais cuidado mais tarde.
Novamente, isso não vai funcionar - teremos uma exceção.
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.expand_dims(tf.eye(2), axis=0)
# Use expand_dims because we want to pass in a tensor of starting values
log_lik_fn = get_log_lik(my_data, n_chains=1)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
return states
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
Cholesky decomposition was not successful. The input might not be valid.
[[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]
Function call stack:
sample
...
Function call stack:
sample
Identificando o problema
InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. Isso não é muito útil. Vamos ver se podemos descobrir mais sobre o que aconteceu.
- Iremos imprimir os parâmetros de cada etapa para que possamos ver o valor para o qual as coisas falham
- Adicionaremos algumas afirmações para nos proteger contra problemas específicos.
Asserções são complicadas porque são operações do TensorFlow e temos que cuidar para que sejam executadas e não sejam otimizadas fora do gráfico. Vale a pena ler esta visão geral de TensorFlow depuração se você não estiver familiarizado com afirmações TF. Você pode forçar explicitamente as afirmações para executar usando tf.control_dependencies (ver os comentários no código abaixo).
Nativo do TensorFlow Print função tem o mesmo comportamento que afirmações - é uma operação, e você precisa tomar alguns cuidados para garantir que ele executa. Print provoca dores de cabeça adicionais quando estamos trabalhando em um notebook: a sua saída é enviado para stderr , e stderr não é exibido na célula. Vamos usar um truque aqui: em vez de usar tf.Print , vamos criar nossa própria operação TensorFlow de impressão via tf.pyfunc . Assim como acontece com as asserções, temos que garantir que nosso método seja executado.
def get_log_lik_verbose(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
def _log_lik(precisions):
# An internal method we'll make into a TensorFlow operation via tf.py_func
def _print_precisions(precisions):
print('precisions:\n', precisions)
return False # operations must return something!
# Turn our method into a TensorFlow operation
print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)
# Assertions are also operations, and some care needs to be taken to ensure
# that they're executed
assert_op = tf.assert_equal(
precisions, tf.linalg.matrix_transpose(precisions),
message='not symmetrical', summarize=4, name='symmetry_check')
# The control_dependencies statement forces its arguments to be executed
# before subsequent operations
with tf.control_dependencies([print_op, assert_op]):
return (log_lik_data(precisions, replicated_data) +
log_lik_prior(precisions))
return _log_lik
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.eye(2)[tf.newaxis, ...]
log_lik_fn = get_log_lik_verbose(my_data)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[ 0.24315196 -0.2761638 ]
[-0.33882257 0.8622 ]]]
assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
[[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]
Function call stack:
sample
...
Function call stack:
sample
Por que isso falha
O primeiro valor de parâmetro novo que o amostrador tenta é uma matriz assimétrica. Isso faz com que a decomposição de Cholesky falhe, uma vez que ela é definida apenas para matrizes simétricas (e definidas positivas).
O problema aqui é que nosso parâmetro de interesse é uma matriz de precisão, e as matrizes de precisão devem ser reais, simétricas e definidas positivas. O amostrador não sabe nada sobre essa restrição (exceto possivelmente por meio de gradientes), então é inteiramente possível que o amostrador proponha um valor inválido, levando a uma exceção, especialmente se o tamanho do passo for grande.
Com o amostrador Hamiltoniano de Monte Carlo, podemos ser capazes de contornar o problema usando um tamanho de passo muito pequeno, uma vez que o gradiente deve manter os parâmetros longe de regiões inválidas, mas tamanhos de passo pequenos significam convergência lenta. Com uma amostra de Metropolis-Hastings, que não sabe nada sobre gradientes, estamos condenados.
Versão 2: reparametrizando para parâmetros irrestritos
Existe uma solução direta para o problema acima: podemos reparametrizar nosso modelo de forma que os novos parâmetros não tenham mais essas restrições. A TFP fornece um conjunto útil de ferramentas - bijetores - para fazer exatamente isso.
Reparametrização com bijetores
Nossa matriz de precisão deve ser real e simétrica; queremos uma parametrização alternativa que não tenha essas restrições. Um ponto de partida é uma fatoração de Cholesky da matriz de precisão. Os fatores de Cholesky ainda são restritos - eles são triangulares inferiores e seus elementos diagonais devem ser positivos. No entanto, se tomarmos o logaritmo das diagonais do fator de Cholesky, os logs não serão mais restritos a serem positivos e, se achatarmos a porção triangular inferior em um vetor 1-D, não teremos mais a restrição triangular inferior . O resultado em nosso caso será um vetor de comprimento 3 sem restrições.
(O manual do Stan tem um grande capítulo sobre o uso de transformações para remover vários tipos de restrições sobre os parâmetros.)
Essa reparametrização tem pouco efeito em nossa função de verossimilhança de log de dados - só temos que inverter nossa transformação para obtermos a matriz de precisão de volta - mas o efeito na anterior é mais complicado. Especificamos que a probabilidade de uma dada matriz de precisão é dada pela distribuição de Wishart; qual é a probabilidade de nossa matriz transformada?
Recorde-se que, se se aplicar uma função monótona \(g\) para um 1-D variável aleatória \(X\), \(Y = g(X)\), a densidade para \(Y\) é dada pela
\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]
A derivada de \(g^{-1}\) termo representa a maneira que \(g\) muda volumes locais. Para variáveis aleatórias de dimensões superiores, o factor de correcção é o valor absoluto do determinante do Jacobiano de \(g^{-1}\) (ver aqui ).
Teremos que adicionar um Jacobiano da transformação inversa em nossa função de verossimilhança logarítmica. Felizmente, da TFP Bijector classe pode cuidar do presente para nós.
O Bijector classe é utilizada para representar as funções inversíveis, suaves utilizadas para a alteração das variáveis em funções de densidade de probabilidade. Bijectors todos têm uma forward() método que realiza um transformar, um inverse() método que inverte-lo, e forward_log_det_jacobian() e inverse_log_det_jacobian() métodos que proporcionam as correcções Jacobianas que necessitam quando reparaterize uma pdf.
TFP fornece uma coleção de bijectors úteis que nós podemos combinar através da composição através da Chain operador para formar transforma bastante complicado. No nosso caso, vamos compor os 3 bijetores a seguir (as operações na cadeia são realizadas da direita para a esquerda):
- A primeira etapa de nossa transformação é realizar uma fatoração de Cholesky na matriz de precisão. Não existe uma classe Bijector para isso; no entanto, o
CholeskyOuterProductbijector converte o produto de 2 factores Cholesky. Podemos usar o inverso do que a operação usando oInvertoperador. - O próximo passo é obter o log dos elementos diagonais do fator de Cholesky. Nós conseguimos isso através da
TransformDiagonalbijector e o inverso daExpbijector. - Finalmente, achatar a parte triangular inferior da matriz de um vector utilizando o inverso do
FillTriangularbijector.
# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
# step 3: flatten the lower triangular portion of the matrix
tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
# step 2: take the log of the diagonals
tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
# step 1: decompose the precision matrix into its Cholesky factors
tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])
# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)
# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)
print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()
print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())
single input: m: [[1. 2.] [2. 8.]] precision_to_unconstrained(m): [0.6931472 2. 0. ] inverse(precision_to_unconstrained(m)): [[1. 2.] [2. 8.]] tensor of inputs: m2: [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]] precision_to_unconstrained(m2): [[0.6931472 2. 0. ] [0. 0. 0. ]] inverse(precision_to_unconstrained(m2)): [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]]
O TransformedDistribution classe automatiza o processo de aplicação de um bijector a uma distribuição e fazer a correção Jacobian necessário log_prob() . Nosso novo prior torna-se:
def log_lik_prior_transformed(transformed_precisions):
rv_precision = tfd.TransformedDistribution(
tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS),
bijector=precision_to_unconstrained,
validate_args=VALIDATE_ARGS)
return rv_precision.log_prob(transformed_precisions)
# Check against the numpy implementation. Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow: -0.84889317 1 numpy: -7.305657151741624 tensorflow: -7.305659
Precisamos apenas inverter a transformação para nossa probabilidade de registro de dados:
precision = precision_to_unconstrained.inverse(transformed_precision)
Como realmente queremos a fatoração de Cholesky da matriz de precisão, seria mais eficiente fazer apenas uma inversão parcial aqui. No entanto, deixaremos a otimização para depois e deixaremos o inverso parcial como um exercício para o leitor.
def log_lik_data_transformed(transformed_precisions, replicated_data):
# We recover the precision matrix by inverting our bijector. This is
# inefficient since we really want the Cholesky decomposition of the
# precision matrix, and the bijector has that in hand during the inversion,
# but we'll worry about efficiency later.
n = tf.shape(transformed_precisions)[0]
precisions = precision_to_unconstrained.inverse(transformed_precisions)
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
transformed_precisions, replicated_data).numpy()
for i in range(precisions.shape[0]):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
Novamente, envolvemos nossas novas funções em um encerramento.
def get_log_lik_transformed(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_transformed(transformed_precisions):
return (log_lik_data_transformed(transformed_precisions, replicated_data) +
log_lik_prior_transformed(transformed_precisions))
return _log_lik_transformed
# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)
[-431.5611]
Amostragem
Agora que não precisamos nos preocupar com a explosão de nosso amostrador por causa de valores de parâmetro inválidos, vamos gerar alguns exemplos reais.
O amostrador funciona com a versão irrestrita de nossos parâmetros, portanto, precisamos transformar nosso valor inicial em sua versão irrestrita. As amostras que geramos também estarão todas em sua forma irrestrita, portanto, precisamos transformá-las de volta. Os bijetores são vetorizados, por isso é fácil de fazer.
# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_value = initial_value_cholesky.dot(
initial_value_cholesky.T)[np.newaxis, ...]
# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
initial_value).numpy()
# Sample!
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)
num_results = 1000
num_burnin_steps = 1000
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
initial_value_transformed,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=lambda _, pkr: pkr.is_accepted,
seed=123)
# transform samples back to their constrained form
precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
Vamos comparar a média da saída de nosso amostrador com a média posterior analítica!
print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Sample mean: [[ 1.4315274 -0.25587553] [-0.25587553 0.5740424 ]]
Estamos muito longe! Vamos descobrir por quê. Primeiro, vamos dar uma olhada em nossos exemplos.
np.reshape(precision_samples, [-1, 2, 2])
array([[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
...,
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]]], dtype=float32)
Ups! Parece que todos têm o mesmo valor. Vamos descobrir por quê.
O kernel_results_ variável é uma tupla nomeado que dá informações sobre a amostragem em cada estado. O is_accepted campo é a chave aqui.
# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))
[False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False] Fraction of samples accepted: 0.0
Todas as nossas amostras foram rejeitadas! Presumivelmente, o tamanho do nosso passo era muito grande. I escolheu stepsize=0.1 puramente arbitrária.
Versão 3: amostragem com um tamanho de etapa adaptável
Como a amostragem com minha escolha arbitrária do tamanho do passo falhou, temos alguns itens da agenda:
- implementar um tamanho de etapa adaptável e
- execute algumas verificações de convergência.
Há um código de exemplo agradável em tensorflow_probability/python/mcmc/hmc.py para a implementação de tamanhos adaptáveis passo. Eu adaptei abaixo.
Note-se que há uma separada sess.run() declaração para cada etapa. Isso é realmente útil para depuração, pois nos permite adicionar facilmente alguns diagnósticos por etapa, se necessário. Por exemplo, podemos mostrar o progresso incremental, o tempo de cada etapa, etc.
Dica: Uma forma aparentemente comum de baralhar o seu amostragem é ter o seu grow gráfico no loop. (A razão para finalizar o gráfico antes de a sessão ser executada é evitar apenas esses problemas.) Se você não estiver usando finalize (), uma verificação de depuração útil se o seu código ficar lento para um rastreamento é imprimir o gráfico tamanho a cada passo via len(mygraph.get_operations()) - Se o comprimento aumenta, provavelmente você está fazendo algo ruim.
Vamos operar 3 cadeias independentes aqui. Fazer algumas comparações entre as cadeias nos ajudará a verificar a convergência.
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values = []
for i in range(N_CHAINS):
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)
initial_values_transformed = precision_to_unconstrained.forward(
initial_values).numpy()
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=hmc,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values_transformed,
kernel=adapted_kernel,
trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
parallel_iterations=1)
# transform samples back to their constrained form
precision_samples = precision_to_unconstrained.inverse(states)
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
Uma verificação rápida: nossa taxa de aceitação durante nossa amostragem está perto de nossa meta de 0,651.
print(np.mean(is_accepted))
0.6190666666666667
Melhor ainda, a média e o desvio padrão de nossa amostra estão próximos do que esperamos da solução analítica.
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96426415 -1.6519215 ] [-1.6519215 3.8614824 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13622096 0.25235635] [0.25235635 0.5394968 ]]
Verificando a convergência
Em geral, não teremos uma solução analítica para verificar, então precisaremos ter certeza de que o amostrador convergiu. Uma verificação padrão é o Gelman-Rubin \(\hat{R}\) estatística, que requer várias cadeias de amostragem. \(\hat{R}\) medidas do grau em que a variância (dos meios) entre cadeias excede o que seria de esperar se as cadeias foram identicamente distribuídos. Valores de \(\hat{R}\) perto de 1 são usados para indicar a convergência aproximada. Veja a fonte para maiores detalhes.
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0038308 1.0005717] [1.0005717 1.0006068]]
Crítica de modelo
Se não tivéssemos uma solução analítica, este seria o momento de fazer algumas críticas ao modelo real.
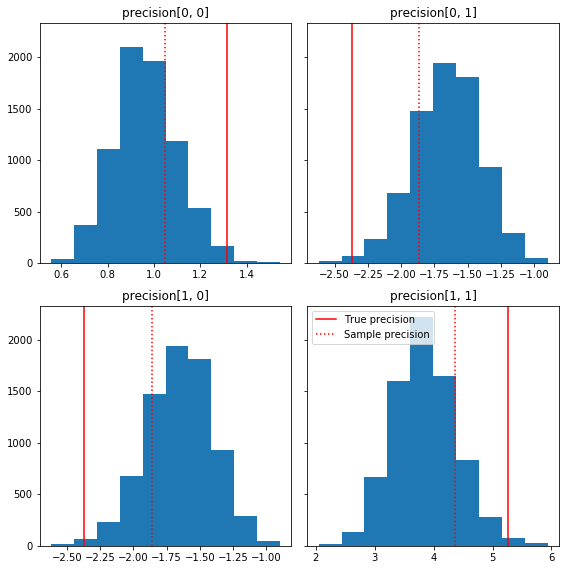
Aqui estão alguns histogramas rápidos dos componentes da amostra em relação à nossa verdade básica (em vermelho). Observe que as amostras foram reduzidas dos valores da matriz de precisão da amostra em direção à matriz de identidade anterior.
fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
for j in range(2):
ax = axes[i, j]
ax.hist(precision_samples_reshaped[:, i, j])
ax.axvline(true_precision[i, j], color='red',
label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':',
label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()
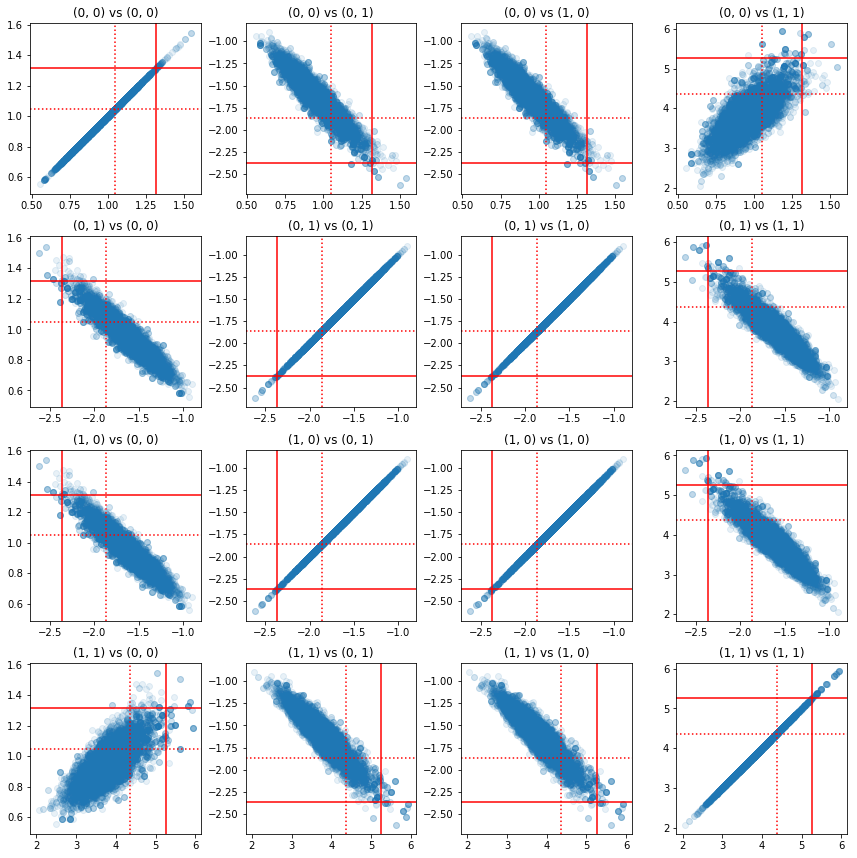
Alguns gráficos de dispersão de pares de componentes de precisão mostram que, por causa da estrutura de correlação do posterior, os verdadeiros valores do posterior não são tão improváveis quanto aparecem nos marginais acima.
fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
for j1 in range(2):
index1 = 2 * i1 + j1
for i2 in range(2):
for j2 in range(2):
index2 = 2 * i2 + j2
ax = axes[index1, index2]
ax.scatter(precision_samples_reshaped[:, i1, j1],
precision_samples_reshaped[:, i2, j2], alpha=0.1)
ax.axvline(true_precision[i1, j1], color='red')
ax.axhline(true_precision[i2, j2], color='red')
ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()
Versão 4: amostragem mais simples de parâmetros restritos
Os bijetores simplificaram a amostragem da matriz de precisão, mas houve uma boa quantidade de conversão manual de e para a representação irrestrita. Existe uma maneira mais fácil!
O TransformedTransitionKernel
O TransformedTransitionKernel simplifica este processo. Ele envolve seu amostrador e lida com todas as conversões. Ele toma como argumento uma lista de bijetores que mapeiam valores de parâmetros irrestritos para valores restritos. Então, aqui precisamos o inverso da precision_to_unconstrained bijector usamos acima. Nós poderíamos simplesmente usar tfb.Invert(precision_to_unconstrained) , mas isso envolveria tomar de inversas de inversas (TensorFlow não é suficiente inteligente para simplificar tf.Invert(tf.Invert()) para tf.Identity()) , então em vez disso, vou apenas escrever um novo bijetor.
Bijetor de restrição
# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
# step 3: take the product of Cholesky factors
tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: map a vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()
print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)
m: [[1.0, 2.0], [2.0, 8.0]] unconstrained_to_precision.inverse(m): [0.6931472 2. 0. ] forward(unconstrained_to_precision.inverse(m)): [[1. 2.] [2. 8.]]
Amostragem com TransformedTransitionKernel
Com a TransformedTransitionKernel , não temos mais a fazer transformações manuais dos nossos parâmetros. Nossos valores iniciais e nossas amostras são todas matrizes de precisão; nós apenas temos que passar nosso (s) bijetor (es) irrestrito (s) para o kernel e ele se encarrega de todas as transformações.
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
return states
precision_samples = sample()
Verificando a convergência
O \(\hat{R}\) de verificação de convergência parece ser bom!
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013582 1.0019467] [1.0019467 1.0011805]]
Comparação com o posterior analítico
Mais uma vez, vamos verificar o posterior analítico.
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96687526 -1.6552585 ] [-1.6552585 3.867676 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329624 0.24913791] [0.24913791 0.53983927]]
Otimizações
Agora que temos tudo funcionando de ponta a ponta, vamos fazer uma versão mais otimizada. A velocidade não importa muito para este exemplo, mas quando as matrizes ficarem maiores, algumas otimizações farão uma grande diferença.
Uma grande melhoria na velocidade que podemos fazer é reparametrizar em termos da decomposição de Cholesky. A razão é que nossa função de verossimilhança de dados requer as matrizes de covariância e precisão. Matrix inversão é caro (\(O(n^3)\) para um \(n \times n\) matriz), e se parametrizar em termos de tanto a covariância ou matriz de precisão, o que precisamos fazer uma inversão para obter a outra.
Como um lembrete, uma verdadeira, definida positiva, simétrica matriz \(M\) pode ser decomposta num produto de forma \(M = L L^T\) onde a matriz \(L\) é triangular inferior e tem diagonais positivos. Dada a decomposição de Cholesky de \(M\), podemos mais eficientemente obter tanto \(M\) (o produto de uma inferior e uma matriz triangular superior) e \(M^{-1}\) (por volta de substituição). A fatoração de Cholesky em si não é barata de calcular, mas se parametrizarmos em termos de fatores de Cholesky, precisamos apenas calcular a fatoração de Choleksy dos valores dos parâmetros iniciais.
Usando a decomposição de Cholesky da matriz de covariância
PTF tem uma versão da distribuição normal multivariada, MultivariateNormalTriL , que é parametrizada em termos do factor de Cholesky da matriz covariância. Portanto, se tivéssemos que parametrizar em termos do fator de Cholesky da matriz de covariância, poderíamos calcular a verossimilhança do log de dados de forma eficiente. O desafio é calcular a probabilidade de log anterior com eficiência semelhante.
Se tivéssemos uma versão da distribuição inversa de Wishart que funcionasse com fatores de Cholesky de amostras, estaríamos prontos. Infelizmente, não. (A equipe gostaria de receber envios de código, no entanto!) Como alternativa, podemos usar uma versão da distribuição de Wishart que funciona com fatores de Cholesky de amostras junto com uma cadeia de bijetores.
No momento, estamos perdendo alguns bijetores de estoque para tornar as coisas realmente eficientes, mas quero mostrar o processo como um exercício e uma ilustração útil do poder dos bijetores da TFP.
Uma distribuição de Wishart que opera em fatores de Cholesky
O Wishart distribuição tem uma bandeira útil, input_output_cholesky , que especifica que as matrizes de entrada e de saída devem ser factores Cholesky. É mais eficiente e numericamente vantajoso trabalhar com os fatores de Cholesky do que com matrizes completas, por isso é desejável. Um ponto importante sobre a semântica da bandeira: é apenas uma indicação de que a representação da entrada e saída para a distribuição deve mudar - não indicar uma re-parametrização total da distribuição, o que implicaria uma correção Jacobian ao log_prob() função. Na verdade, queremos fazer essa reparametrização completa, então construiremos nossa própria distribuição.
# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices. Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).
class CholeskyWishart(tfd.TransformedDistribution):
"""Wishart distribution reparameterized to use Cholesky factors."""
def __init__(self,
df,
scale_tril,
validate_args=False,
allow_nan_stats=True,
name='CholeskyWishart'):
# Wishart has a bunch of methods that we want to support but not
# implement. We'll subclass TransformedDistribution here to take care of
# those. We'll override the few for which speed is critical and implement
# them with a separate Wishart for which input_output_cholesky=True
super(CholeskyWishart, self).__init__(
distribution=tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=False,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
validate_args=validate_args,
name=name
)
# Here's the Cholesky distribution we'll use for log_prob() and sample()
self.cholesky = tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=True,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats)
def _log_prob(self, x):
return (self.cholesky.log_prob(x) +
self.bijector.inverse_log_det_jacobian(x, event_ndims=2))
def _sample_n(self, n, seed=None):
return self.cholesky._sample_n(n, seed)
# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
@tf.function(autograph=False)
def compute_log_prob(m):
w_transformed = tfd.TransformedDistribution(
tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
w_optimized = CholeskyWishart(
df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
log_prob_transformed = w_transformed.log_prob(m)
log_prob_optimized = w_optimized.log_prob(m)
return log_prob_transformed, log_prob_optimized
for matrix in [np.eye(2, dtype=np.float32),
np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
log_prob_transformed, log_prob_optimized = [
t.numpy() for t in compute_log_prob(matrix)]
print('Transformed Wishart:', log_prob_transformed)
print('Optimized Wishart', log_prob_optimized)
Transformed Wishart: -0.84889317 Optimized Wishart -0.84889317 Transformed Wishart: -99.269455 Optimized Wishart -99.269455
Construindo uma distribuição inversa de Wishart
Nós temos a matriz covariância \(C\) decomposto em \(C = L L^T\) onde \(L\) é triangular inferior e tem uma diagonal positivo. Queremos saber a probabilidade de \(L\) dado que \(C \sim W^{-1}(\nu, V)\) onde \(W^{-1}\) é o inverso distribuição Wishart.
A distribuição Wishart inversa tem a propriedade que se \(C \sim W^{-1}(\nu, V)\), então a matriz de precisão \(C^{-1} \sim W(\nu, V^{-1})\). Assim, podemos obter a probabilidade de \(L\) através de um TransformedDistribution que toma como parâmetros a distribuição Wishart e uma bijector que mapeia o fator Cholesky da matriz de precisão para um fator Cholesky de seu inverso.
Uma maneira simples (mas não super eficiente) a começar a partir do fator Cholesky de \(C^{-1}\) para \(L\) é inverter o fator Cholesky por trás de problemas, em seguida, formando a matriz de covariância destes factores invertidos, e depois fazer uma fatoração de Cholesky .
Deixe a decomposição de Cholesky de \(C^{-1} = M M^T\). \(M\) é triangular inferior, para que possamos inverter-lo usando o MatrixInverseTriL bijector.
Formando \(C\) de \(M^{-1}\) é um pouco complicado: \(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\). \(M\) é triangular inferior, de modo \(M^{-1}\) também será menor triangular, e \(M^{-T}\) será triangular superior. O CholeskyOuterProduct() bijector só funciona com matrizes triangulares inferiores, por isso não podemos usá-lo para formar \(C\) de \(M^{-T}\). Nossa solução alternativa é uma cadeia de bijetores que permutam as linhas e colunas de uma matriz.
Felizmente esta lógica é encapsulado no CholeskyToInvCholesky bijector!
Combinando todas as peças
# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()
print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)
numpy = [[ 1.0307764 0. ] [-0.03031695 0.12126781]] bijector = [[ 1.0307764 0. ] [-0.03031695 0.12126781]]
Nossa distribuição final
Nosso Wishart inverso operando em fatores de Cholesky é o seguinte:
inverse_wishart_cholesky = tfd.TransformedDistribution(
distribution=CholeskyWishart(
df=PRIOR_DF,
scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
bijector=tfb.CholeskyToInvCholesky())
Temos nosso Wishart inverso, mas é meio lento porque temos que fazer uma decomposição de Cholesky no bijetor. Vamos voltar à parametrização da matriz de precisão e ver o que podemos fazer para otimização.
Versão final (!): Usando a decomposição de Cholesky da matriz de precisão
Uma abordagem alternativa é trabalhar com fatores de Cholesky da matriz de precisão. Aqui, a função de verossimilhança anterior é fácil de calcular, mas a função de verossimilhança de registro de dados dá mais trabalho, pois a TFP não tem uma versão da normal multivariada que é parametrizada por precisão.
Probabilidade de registro anterior otimizado
Usamos o CholeskyWishart distribuição construímos acima para construir o anterior.
# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
def log_lik_prior_cholesky(precisions_cholesky):
rv_precision = CholeskyWishart(
df=PRIOR_DF,
scale_tril=PRIOR_SCALE_CHOLESKY,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions_cholesky)
# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
distribution=tfd.WishartTriL(
df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow slow:', lik_tf_slow[i])
print('tensorflow fast:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow slow: -0.84889317 tensorflow fast: -0.84889317 1 numpy: -7.442875031036973 tensorflow slow: -7.442877 tensorflow fast: -7.442876
Probabilidade de registro de dados otimizado
We can use TFP's bijectors to build our own version of the multivariate normal. Here is the key idea:
Suppose I have a column vector \(X\) whose elements are iid samples of \(N(0, 1)\). We have \(\text{mean}(X) = 0\) and \(\text{cov}(X) = I\)
Now let \(Y = A X + b\). We have \(\text{mean}(Y) = b\) and \(\text{cov}(Y) = A A^T\)
Hence we can make vectors with mean \(b\) and covariance \(C\) using the affine transform \(Ax+b\) to vectors of iid standard Normal samples provided \(A A^T = C\). The Cholesky decomposition of \(C\) has the desired property. However, there are other solutions.
Let \(P = C^{-1}\) and let the Cholesky decomposition of \(P\) be \(B\), ie \(B B^T = P\). Now
\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)
So another way to get our desired mean and covariance is to use the affine transform \(Y=B^{-T}X + b\).
Our approach (courtesy of this notebook ):
- Use
tfd.Independent()to combine a batch of 1-DNormalrandom variables into a single multi-dimensional random variable. Thereinterpreted_batch_ndimsparameter forIndependent()specifies the number of batch dimensions that should be reinterpreted as event dimensions. In our case we create a 1-D batch of length 2 that we transform into a 1-D event of length 2, soreinterpreted_batch_ndims=1. - Apply a bijector to add the desired covariance:
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True)). Note that above we're multiplying our iid normal random variables by the transpose of the inverse of the Cholesky factor of the precision matrix \((B^{-T}X)\). Thetfb.Inverttakes care of inverting \(B\), and theadjoint=Trueflag performs the transpose. - Apply a bijector to add the desired offset:
tfb.Shift(shift=shift)Note that we have to do the shift as a separate step from the initial inverted affine transform because otherwise the inverted scale is applied to the shift (since the inverse of \(y=Ax+b\) is \(x=A^{-1}y - A^{-1}b\)).
class MVNPrecisionCholesky(tfd.TransformedDistribution):
"""Multivariate normal parameterized by loc and Cholesky precision matrix."""
def __init__(self, loc, precision_cholesky, name=None):
super(MVNPrecisionCholesky, self).__init__(
distribution=tfd.Independent(
tfd.Normal(loc=tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
adjoint=True)),
]),
name=name)
@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
n = tf.shape(precisions_cholesky)[0] # number of precision matrices
rv_data = MVNPrecisionCholesky(
loc=tf.zeros([n, 2]),
precision_cholesky=precisions_cholesky)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.81824
Combined log likelihood function
Now we combine our prior and data log likelihood functions in a closure.
def get_log_lik_cholesky(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_cholesky(precisions_cholesky):
return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
log_lik_prior_cholesky(precisions_cholesky))
return _log_lik_cholesky
Constraining bijector
Our samples are constrained to be valid Cholesky factors, which means they must be lower triangular matrices with positive diagonals. The TransformedTransitionKernel needs a bijector that maps unconstrained tensors to/from tensors with our desired constraints. We've removed the Cholesky decomposition from the bijector's inverse, which speeds things up.
unconstrained_to_precision_cholesky = tfb.Chain([
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: expand the vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)
precisions_cholesky: [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]] inv: [[ 0.0000000e+00 0.0000000e+00 0.0000000e+00] [ 3.5762781e-07 -2.0647411e+00 1.3721828e-01]] fwd(inv): [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]]
Initial values
We generate a tensor of initial values. We're working with Cholesky factors, so we generate some Cholesky factor initial values.
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values_cholesky = []
for i in range(N_CHAINS):
initial_values_cholesky.append(np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)
Sampling
We sample N_CHAINS chains using the TransformedTransitionKernel .
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_cholesky(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
samples = tf.linalg.matmul(states, states, transpose_b=True)
return samples
precision_samples = sample()
Convergence check
A quick convergence check looks good:
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013583 1.0019467] [1.0019467 1.0011804]]
Comparing results to the analytic posterior
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])
And again, the sample means and standard deviations match those of the analytic posterior.
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.9668749 -1.6552604] [-1.6552604 3.8676758]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329637 0.24913797] [0.24913797 0.53983945]]
Ok, all done! We've got our optimized sampler working.

